Молекула водорода Метод валентных схем метод Гайтлера-Лондона

Молекула водорода Метод валентных схем (метод Гайтлера-Лондона )

Построение волновой функции • Для построения многоэлектронной волновой функции. Гайтлер и Лондон использовали 1 s орбитали атомов водорода, радиальная часть которых записывается в виде (в атомной системе единиц) • Таким образом, используется модель, в которой молекула есть совокупность атомов, представленных их атомными орбиталями. Атомы в молекуле сохраняют свою индивидуальность, и электрон считается входящим в состав того или другого атома.

Построим теперь все возможные двухэлектронные функции молекулы водорода из 1 s атомных орбиталей. Обозначим атомы водорода Ha и Hb, а их атомные орбитали - 1 sa и 1 sb:

Двухэлектронные функции • Будем записывать функцию в виде произведения двух частей: пространственной и спиновой. Спиновые функции для двухэлектронной системы известны: синглетная функция антисимметрична, а триплетная функция симметрична относительно перестановок спинов электронов. Полная волновая функция должна быть антисимметрична относительно перестановкой координат и спинов электронов, поэтому пространственные функция синглетных состояний симметрична, а триплетных состояний – антисимметрична относительно перестановки координат электронов. Кроме того, при перестановке одинаковых атомов водорода внутри молекулы распределение электронной плотности не может меняться, поэтому при такой операции полная функция должна или оставаться неизменной, или менять знак. Сказанное позволяет построить следующие двухэлектронные пространственные функции (в скобках указан номер электрона, от координат которого зависит данная одноэлектронная функция – атомная орбиталь):

Двухэлектронные функции Для всех приведенных функций нормировочный множитель N равен , знак в подкоренном выражении определяется знаком в функциях

Выпишем все возможные полные функции молекулы водорода (с учетом возможных проекций спина для состояния с S=1):

Полный базис • Можно убедится путем непосредственного перебора, что приведенные шесть функций представляют собой полный базис двухэлектронных функций, то есть все те функции, удовлетворяющие принципу Паули, которые можно построить для молекулы водорода из атомных орбиталей 1 sa и 1 sb и спиновых функций и . Решения, полученные с этими шестью функциями, будут точными для выбранного электронного базиса с фиксированным значением экспоненциального параметра =1.

Классификация состояний • Таким образом, всего имеется четыре состояния: три синглетных и одно триплетное. Первые две функции можно наглядно представить себе следующим образом: первый электрон находится на атомной орбитали одного из атомов водорода, а второй электрон – на орбитали второго атома водорода. Синглетную функцию I рассматривают как модель ковалентной связи, в которой со стороны каждого атома участвует по одному электрону. Функции III и IV можно рассматривать как суперпозицию структур, описывющих ионные связи, в которых один из атомов – a или b - становится анионом (1 sa(1)1 sa(2) или 1 sb(1)1 sb(2)), а второй – катионом Н+. Поскольку общепризнано, что в молекуле Н 2 реализуется простая ковалентная связь, начнем более подробное рассмотрение с “ковалентных” структур I и II.

Исключаем спин • Запишем выражение для полной энергии молекулы водорода в состоянии К ( К(1, 2)= К(1, 2), где К(1, 2)– спиновая компонента функции К):

В атомных единицах

Так как вид функций 1 sa и 1 sb одинаков, то при интегрировании появляется ряд одинаковых интегралов, например

Компактное выражение

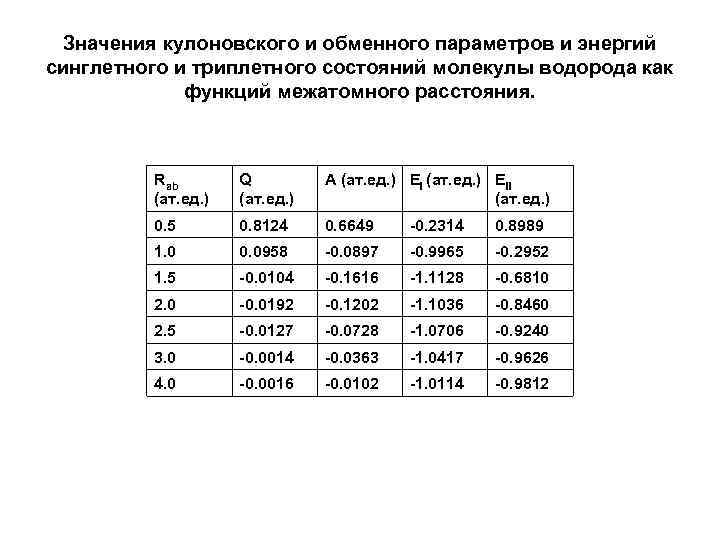Значения кулоновского и обменного параметров и энергий синглетного и триплетного состояний молекулы водорода как функций межатомного расстояния. Rab (ат. ед. ) Q (ат. ед. ) A (ат. ед. ) EII (ат. ед. ) 0. 5 0. 8124 0. 6649 -0. 2314 0. 8989 1. 0 0. 0958 -0. 0897 -0. 9965 -0. 2952 1. 5 -0. 0104 -0. 1616 -1. 1128 -0. 6810 2. 0 -0. 0192 -0. 1202 -1. 1036 -0. 8460 2. 5 -0. 0127 -0. 0728 -1. 0706 -0. 9240 3. 0 -0. 0014 -0. 0363 -1. 0417 -0. 9626 4. 0 -0. 0016 -0. 0102 -1. 0114 -0. 9812

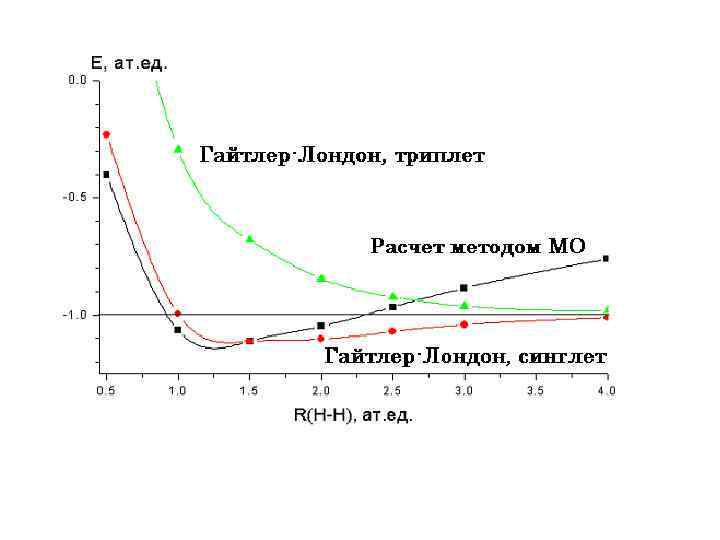
Расчет • Потенциальная кривая для этого состояния имеет минимум при Rab=0, 87 Å (экспериментальное значение – 0. 74 Å), то естьсинглетное состояние является связывающим. Энергия диссоциации (без учета поправки на нулевые колебания) равна 3, 14 э. В (экспериментальное значение – 4, 7466 э. В). Потенциальная кривая триплетного состояния показывает, что возбужденная молекула водорода неустойчива и спонтанно диссоциирует с образованием двух атомов водорода (что полностью соответствует эксперименту).

Пути уточнения модели • 1) Варьирование экспоненциального параметра • Значение энергии при Rab = 0. 741 Å ( = 1. 166) равно – 1. 139 ат. ед. , что соответствует энергии диссоциации 3. 782 э. В (80 % от экспериментального значения). • 2) Включение ионного члена =С 1 ков. + С 2 ионн. . ков. + ионн. Небольшой выигрыш в энергии (De=3. 23 э. В) сопровождается некоторым ухудшением рассчитанного значения межатомного расстояния (Re=0. 88 Å).

Расчет Вейнбаума • К заметному улучшению приводит одновременное варьирование как экспоненциального параметра , так и линейного параметра (расчеты Вейнбаума, =1. 193, De=4. 02 э. В, Re=0. 748 Å). Полученная в этих расчетах энергия диссоциации составляет 85 % от экспериментального значения.

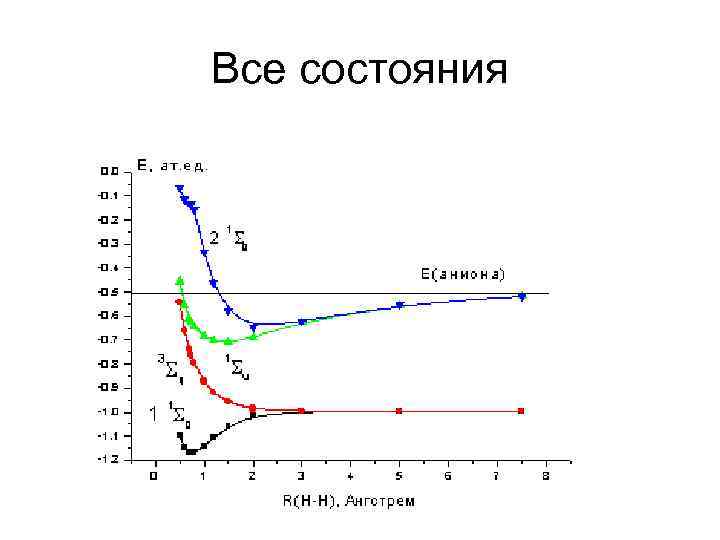Все состояния

Расчеты Джеймса и Кулиджа Энергия диссоциации, рассчитанная с этой функцией, равна 4. 53 э. В.

Метод МО

Добавим функцию . Ее можно рассматривать как конфигурацию, полученную в результате двукратного возбуждения с орбитали g на орбиталь u.

На бесконечно большом расстоянии