Module D Waiting Line Models Elements of

Module D Waiting Line Models

Elements of Waiting Line Analysis ü Queue ü A single waiting line ü Waiting line system consists of ü Arrivals ü Servers ü Waiting line structures

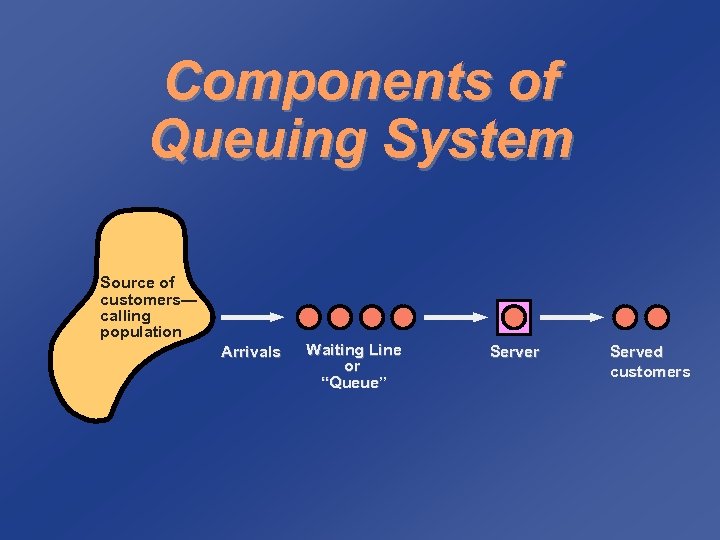Components of Queuing System Source of customers— calling population Arrivals Waiting Line or “Queue” Server Served customers

Elements of a Waiting Line ü Calling population ü Source of customers ü Infinite - large enough that one more customer can always arrive to be served ü Finite - limited number of potential customers ü Arrival rate ( ) ü Frequency of customer arrivals at waiting line system ü Typically follows Poisson distribution

Elements of a Waiting Line ü Service time ü Often follows negative exponential distribution ü Average service rate = ü Arrival rate ( ) must be less than service rate or system never clears out

Elements of a Waiting Line ü Queue discipline ü Order in which customers are served ü First come, first served is most common ü Length can be infinite or finite ü Infinite is most common ü Finite is limited by some physical structure (not covered)

Basic Waiting Line Structures ü Channels are the number of parallel servers ü Phases denote number of sequential servers the customer must go through

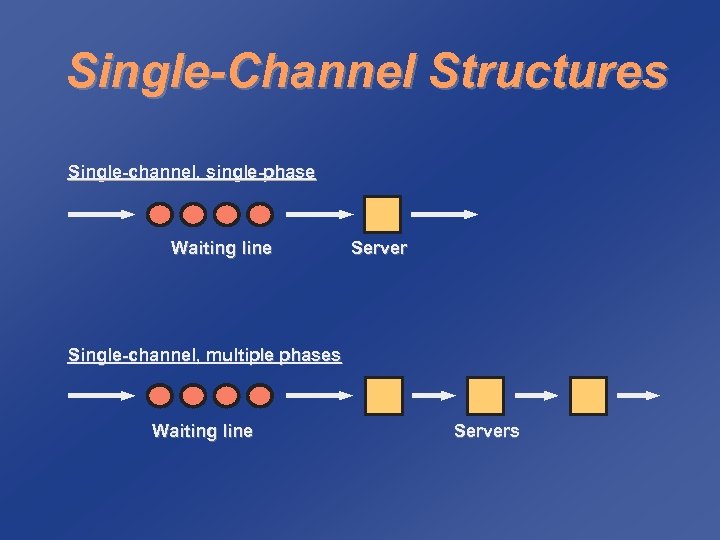Single-Channel Structures Single-channel, single-phase Waiting line Server Single-channel, multiple phases Waiting line Servers

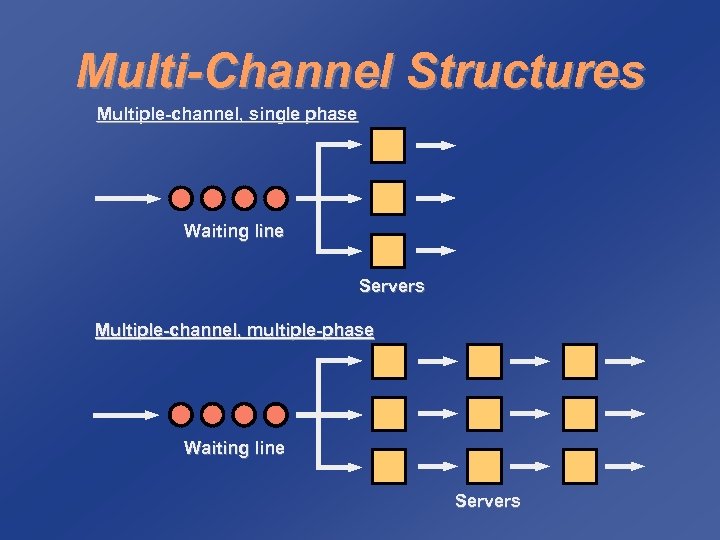Multi-Channel Structures Multiple-channel, single phase Waiting line Servers Multiple-channel, multiple-phase Waiting line Servers

Operating Characteristics ü Mathematics of queuing theory does not provide optimal or best solutions ü Operating characteristics are computed that describe system performance ü Steady state is constant, average value for performance characteristics that the system will reach after a long time

Operating Characteristics NOTATION OPERATING CHARACTERISTIC L Average number of customers in the system (waiting and being served) Lq Average number of customers in the waiting line W Average time a customer spends in the system (waiting and being served) Wq Average time a customer spends waiting in line

Operating Characteristics NOTATION OPERATING CHARACTERISTIC P 0 Probability of no (zero) customers in the system Pn Probability of n customers in the system Utilization rate; the proportion of time the system is in use

Single-Channel, Single. Phase Models ü All assume Poisson arrival rate ü Variations ü Exponential service times ü Constant service times ü Others are not considered

Basic Single-Server Model ü Assumptions: ü Poisson arrival rate ü Exponential service times ü First-come, first-served queue discipline ü Infinite queue length ü Infinite calling population ü = mean arrival rate ü = mean service rate

Formulas for Single. Server Model Probability that no customers are in the system (either in the queue or being served) Probability of exactly n customers in the system Average number of customers in the waiting line P 0 = 1 - Pn = = n • P 0 n Lq = ( - ) L = 1 -

Formulas for Single. Server Model Average time a customer spends in the queuing system 1 L W = = - Average time a customer spends waiting in line to be served Wq = Probability that the server is busy and the customer has to wait Probability that the server is idle and a customer can be served = ( - ) I = 1 - = P 0

A Single-Server Model Given = 24 per hour, = 30 customers per hour Probability of no customers in the system P 0 = 1 - 0. 20 Average number of customers in the system L = Average number of customers waiting in line (24)2 2 Lq = = = 3. 2 30(30 - 24) ( - ) 24 = 130 24 = 30 - 24 - = =4

A Single-Server Model Given = 24 per hour, = 30 customers per hour 1 1 = = 0. 167 hour - 30 - 24 Average time in the system per customer W = Average time waiting in line per customer Wq = Probability that the server will be busy and the customer must wait = Probability the server will be idle I = 1 - 0. 80 = 0. 20 24 = = 0. 133 30(30 - 24) ( - ) 24 = = 0. 80 30

Waiting Line Cost Analysis To improve customer services management wants to test two alternatives to reduce customer waiting time: 1. Another employee to pack up purchases 2. Another checkout counter

Waiting Line Cost Analysis ü Add extra employee to increase service rate from 30 to 40 customers per hour ü Extra employee costs $150/week ü Each one-minute reduction in customer waiting time avoids $75 in lost sales ü Waiting time with one employee = 8 minutes Wq = 0. 038 hours = 2. 25 minutes 8. 00 - 2. 25 = 5. 75 minutes reduction 5. 75 x $75/minute/week = $431. 25 per week New employee saves $431. 25 - $150. 00 = $281. 25/wk

Waiting Line Cost Analysis ü New counter costs $6000 plus $200 per week for checker ü Customers divide themselves between two checkout lines ü Arrival rate is reduced from = 24 to = 12 ü Service rate for each checker is = 30 Wq = 0. 022 hours = 1. 33 minutes 8. 00 - 1. 33 = 6. 67 minutes 6. 67 x $75/minute/week = $500. 00/wk - $200 = $300/wk Counter is paid off in 6000/300 = 20 weeks

Waiting Line Cost Analysis ü Adding an employee results in savings and improved customer service ü Adding a new counter results in slightly greater savings and improved customer service, but only after the initial investment has been recovered ü A new counter results in more idle time for employees ü A new counter would take up potentially valuable floor space

Constant Service Times ü Constant service times occur with machinery and automated equipment ü Constant service times are a special case of the single-server model with general or undefined service times

Operating Characteristics for Constant Service Times Probability that no customers are in system P 0 = 1 - Average number of customers in queue 2 Lq = 2 ( - ) Average number of customers in system L = Lq +

Operating Characteristics for Constant Service Times Average time customer spends in queue Lq Wq = Average time customer spends in the system W = Wq + Probability that the server is busy = 1

Constant Service Times Automated car wash with service time = 4. 5 min Cars arrive at rate = 10/hour (Poisson) = 60/4. 5 = 13. 3/hour (10)2 2 Lq = = = 1. 14 cars waiting 2(13. 3)(13. 3 - 10) 2 ( - ) Wq = Lq = 1. 14/10 =. 114 hour or 6. 84 minutes

Multiple-Channel, Single-Phase Models ü Two or more independent servers serve a single waiting line ü Poisson arrivals, exponential service, infinite calling population ü s > P 0 = 1 n=s-1 n=0 1 n! n 1 + s! s s s -

Multiple-Channel, Single-Phase Models ü Two or more independent serverscan be a Computing P 0 serve single waiting line time-consuming. Tables can used to ü Poisson arrivals, exponential service, find P infinite calling population 0 for selected values of and s. ü s > P 0 = 1 n=s-1 n=0 1 n! n 1 + s! s s s -

Multiple-Channel, Single-Phase Models Probability of exactly n customers in the system Probability an arriving customer must wait Average number of customers in system 1 s! s P 0 , for n > s n 1 n! Pw = L = 1 s! sn-s Pn = n P 0 , for n > s s P 0 s - ( / )s (s - 1)!(s - )2 P 0 +

Multiple-Channel, Single-Phase Models L Average time customer spends in system W = Average number of customers in queue Lq = L - Average time customer spends in queue Lq 1 Wq = W = Utilization factor = /s