MODULE — 3 Financial Mathematics Use simple and

MODULE - 3 Financial Mathematics Use simple and compound growth formulae to solve problems, including: Interest, hire – purchase, inflation, population growth and other real life problems (LO 1 AS 4) Demonstrate an understanding of the implications of fluctuation, Foreign exchange rates (petrol price, imports, exports, overseas travel). (LO 1 AS 5) n. Solve non – routine, unseen problems. n(LO 1 AS 6)

NOTES: When money is borrowed from or invested in a financial institution, interest is charged/paid. When you get a loan from a bank, you must pay interest on the borrowed money. In other words you pay more to the bank than you had borrowed. However, when you save/invest money in a bank, or even better, in unit trusts or shares, the interest is then paid to you by the financial institution so your money grows.

Interest depends on three factors: n The amount of money invested or loaned, represented by the symbol, P. n The duration of the investment or loan represented by the symbol, . n The interest rate over a period of time, represented by the symbol , n In Financial Math’s, we say that

(A) Simple Interest n If interest is based only on the original sum of money, then it is called simple interest.

For example: n n n n R 1500 is invested for 2 years at 18% per annum (p. a. ) simple interest. The accumulated amount (future value) after 1 year is: A = R 1500 + 18% of R 1500 = R 1500 + x Rl 500 = R 1500 + 0, 18 x R 1500 = R 1770 (Notice that the interest made in the first year is R 270) The future value after 2 years is: A = R 1770 + 18% of R 1500 = R 1770 + 0, 18 x Rl 500 = R 2040 (Notice that the interest made in the second year is also R 270 and R 540 over the first two years) A useful formula which helps us to calculate the future value (A) of an original amount P, which has been invested for n years at a rate of r% simple interest is: A = P(1 + i. n) where: P = present value of the investment (original amount at the beginning) A = accumulated mount (future value) of the investment after n periods n = time period for the simple interest rate r (%) In the previous example, we can calculate the future value of R 1500 after 2 years using this formula: A = P(1 + i. n) Where: P = R 1500 ; I = 18% p. a ; n = 2 years A = R 1500(1 + 0, 18 x 2) A = R 2040

Example 1 n n n R 50 000 is invested for 18 years at an interest rate of 16% per annum simple interest. Find: (a) the accumulated amount (future value) of the investment. (b) the simple interest received at the end of the 18 years. (c) the simple interest received each year. P = R 50 000 ; I = 0. 16 p. a ; n = 18 years n (a) A = P(1 + i. n) A = R 50 000 (1 + 0, 16. 18) A = R 194 000 (b) Interest received: = R 194 000 – R 50 000 = R 144 000. n (c) Interest received annually = n n n

Example 2 n How much was invested four years ago if the value of the investment is currently R 8000? The interest rate was 7% per annum simple interest. A = P(I + I. n) A = R 8000 ; n = 4 years ; I = 0. 07 R 7000 = P(1 + 0, 07 x 4) R 7000 = P(l + 0, 28) R 7000 = P(1, 28) n P = R 5468, 75 n n n

Example 3 n n n n n An amount of R 1 600 accumulates to R 3000 after 4 years. Find the interest rate if the investment earned simple interest. A = P(1 + i. n) A = R 3000 ; P = R 1600 ; n = 4 years (48 months) R 3000 = R 1600(1 + i. 4) R 3000 = R 1600 + 4800 i R 3000 – R 1600 = 4800 i R 1500 4800 = i i = 0, 3125 r = 31, 25%

EXERCISE 1 1. Sarah invests R 5000 for 6 years at a simple interest rate of 8% per annum. Calculate: n (a) the future value of the investment. n (b) the simple interest received at the end of the 6 th year. n (c) the simple interest received each year.

2. Kabelo invests R 15000 for 15 years at a simple interest rate of 8% per annum. Calculate: n (a) the future value of the investment. n (b) the simple interest received at the end of the 15 years. n (c) the simple interest received each year. n

3. In 3 years’ time John wants to have saved R 25 000 in order to visit his cousin who lives in England. He manages to receive an interest rate of 12% per annum simple interest. n How much must he invest now in order to achieve his goal?

4. Sandesh wants to invest a sum of money now so as to afford a new play station costing R 5000, three years from now. He receives a simple interest rate of 6% per annum. n Calculate how much should Sandesh invest?

5. Calculate how long it would take an investment of R 3900 to grow to a value of R 5500 if the simple interest rate received is 12% per annum.

6. Calculate how long it would take for an investment of R 5800 to double if the simple interest rate is 14% per annum.

7. In order for R 5000 to grow to R 10000 over a period of 5 years, what simple interest rate would you need to secure?

8. Ronald has R 5000 to invest and wishes to increase this amount to R 6000 over a period of 2, 5 years. What simple interest rate will he need to receive in order to achieve this?

9. An amount of R 2000 is invested at 14% p. a. simple interest. A further R 1400 is invested at 12% p. a. simple interest. By when will both investments have the same accumulated values?

Hire Purchase Agreements n A Hire Purchase Agreement (HP) is a shortterm loan. Furniture, cars and household appliances, such as refrigerators, are generally bought on HP. n Buyers sign an agreement with the seller to pay a specified amount per month. n The interest paid on a hire purchase loan is simple interest and it is calculated on the full value of the loan over the repayment period. n Normally a deposit is paid initially and the balance is paid over a short time period

Example 1 n n Pumzile buys a DVD player for R 7 800. She takes out a hire-purchase loan involving equal monthly payments over 2 years. The interest rate charged is 14, 5% per annum simple interest. She also takes out an insurance premium of Rl 0, 35 per month, to cover the cost of damage or theft. Calculate: (a) the actual amount paid for the DVD player. (b) the interest paid. (c) how much must be paid each month.

n (a) A = P(1 + i. n) years (24 months) [P = R 7 800 ; n=2 I = 14, 5 % p. a] A = R 7 800 [1 + (0, 145)(2)] A = R 10 062 n (b) Interest paid = R 10 062 – R 7 800 = R 2 262 n (c) The monthly loan repayments: R 10 062 24 months = R 419, 25 Add in the monthly insurance premium, the total amount to be paid each month is: R 419, 25 + R 10, 35 = R 429, 60 p. m

Example 2 n Jo - Ann buys a laptop priced at R 13 495. She takes out a 12 -month hire purchase agreement. She pays a deposit of 20% and the interest charged on the balance is 15% per annum simple interest. What will she actually pay for the laptop and what will her monthly payments be?

Deposit : = 0, 2 x R 13 495 = R 2 699 Balance on HP: = R 13 495 - R 2 699 = R 10 796 A = R 10 796(1 + 0, 15 x 1) A = Rl 2 415, 40 Jo - Ann will actually pay : R 2 699 + R 12 415 = R 15 114 for the laptop. Her monthly repayments will be: R 15 114 12 = R 1 259, 50 p. m n

Example 3 A car radio costs R 960. Megan buys her car radio on HP and agrees to pay a deposit of Rl 00 and 24 monthly repayments of R 45 p. m Calculate: (a) the total simple interest paid. (b) the rate of simple interest. n

(a) Total amount paid: = Rl 00 + 24 x R 45 = R 1 180 Total interest paid: = R 1 180 – R 960 = R 220 The deposit of Rl 00 is paid at the start of the HP, so the balance (P) to be paid is therefore R 860. n

n The 24 amounts of R 45 that must be paid will add up to R 1 032, which is A, the final value. P = R 860 ; A = R 1 080; n = 24 months ; I = ? A = P (l + i. n) R 1 080 = R 860(1 + I x 2) R 1 080 R 860 = 1 + 2 i 1, 255813953 – 1 = 2 i 0. 255813953 = 2 i 0, 2558139532 2 = i r = 12, 8 %

EXERCISE 2 1. Mpho buys a furniture suite for R 9895. He takes out a hire-purchase loan involving equal monthly payments over five years. The interest rate charged is 15, 25% per annum simple interest. He also takes out an insurance premium of RI 2 per month to cover the cost of damage or theft. Calculate: (a) the actual amount paid for the furniture suite. (b) the interest paid. (c) how much must be paid each month.

2. Greg buys a laptop priced at R 12 535. He takes out a 24 -month hire purchase agreement. He pays a deposit of 10% and the interest charged on the balance is 16, 125% per annum simple interest. What will he actually pay for the laptop and what will his monthly payments be?

3. A play station 11 costs R 4593. Daniel buys a play station on HP and agrees to pay a deposit of R 450 and 36 monthly payments of R 150. n Calculate the total simple interest paid and the rate of simple interest.

4. A hire purchase contract for a sound system requires OJ to pay a deposit of R 550 and then make 6 monthly payments of R 185. If the price of the sound system is R 1 401. n Calculate the total simple interest paid and the rate of simple interest.

5. Mr Sibanda bought a computer costing R 22 253 on hire purchase. He traded in an old computer for R 2000 and paid a deposit of R 1500. The balance was paid by means of monthly installments of RI 120, 50 over two years. Calculate the total simple interest paid and the rate of simple interest.

6. Ernst wants to buy a computer. He can only afford R 500 per month. He wants to take out a hire purchase loan over 36 months at an interest rate of 24% per annum. Calculate the price of the computer that he can afford to buy.

Compound Interest n n If interest is calculated on the original sum plus interest already earned, then it is called compound interest. In practice, financial institutions use compound interest. The interest earned or growth on your money is reinvested back into your investment. Consider, for example, an amount of R 5500 invested at 5% per annum compound interest for a period of 2 years.

n The future value of the investment after 1 year is: (Notice that the interest made in the first year is R 275) n The future value of the investment after 2 years is:

(Notice that the interest made in the second year is R 288, 75, which is more than the interest made in the first year)

n n n With simple interest, the amount of interest received or paid is exactly the same each year. However, with compound interest, the amount of interest increases each year. This is great if you are saving money, but not too great if you have borrowed money from the bank. A useful formula which helps us to calculate the future value (A) of an original amount P, which has been invested for n years at a rate of r% compound interest is: where: P = present value of the investment (original amount at the beginning) A = accumulated amount (future value) of the investment after n periods n = time period

for the compound interest rate r% (decimal equivalent) n In the previous example, we can calculate the future value of R 5000 after 2 years using this formula: n

Example 1 Petro invests R 8000 for 9 years at 15% p. a. compounded annually. Find the final value of her investment after 9 years and the interest she receives.

Interest received = R 28 143, 01 - R 8000 = R 20 143, 01 The money invested, R 8000, grows in value to R 28 143, 01 over the 9 -year duration of the loan due to interest being earned on the money. Conclusion: The value of A is therefore greater than P.

Example 2 Jamy takes out a loan in order to start his small car – wash business. Three years after granting the loan, he agrees to repay the loan by means of a once off payment of R 405 000. The bank charges him an interest rate of 23% p. a. compounded annually. How much money did he borrow from the bank? (what is the present value of the loan)?

Example 3 R 4250 is invested for 6 years and grows to R 14 740. Find the interest rate if interest is compounded annually.

EXERCISE 3 Find the end value of R 1300 invested for 6 years at (a) 14, 78% p. a. compound interest. (b) 18, 70% p. a. compound interest. 2. Find the present value of an amount which accumulated to R 2228, 40 in 5 years at: (a) 11, 86% p. a. compound interest. (b) 12, 73% p. a. compound interest. 1.

3. Jana invests R 100 500 in an account paying 17, 25% p. a. compounded annually. Calculate the future value of his investment after 18 years. 4. Patrick borrows money from a bank in order to finance his new business. The bank charges him an interest rate of 14, 75% p. a. compounded annually. Calculate the present value of the loan (the amount he originally borrowed), if he pays off the loan 8 years from now with a payment of R 500 000. 5. R 6000 is invested for 5 years and grows to R 9000. Find the interest rate if interest is compounded annually. 6. Find the annual compound interest rate that makes R 2500 double in 5 years.

7. R 50 000 is invested at 10% p. a. simple interest for 3 years. Thereafter, the total amount is reinvested in a different financial institution at 25% p. a. compound interest for 2 more years. What is the future value of the investment after the five-year period?

Inflation is the steady compounded increase in prices over time throughout the economy. When money is invested, it is therefore essential to take into account the effect of inflation. If the interest rate on your investments is below the current inflation rate, then the buying power of your money in the future will rapidly decline.

Example 1 A motorcar currently costs R 800 000. If the rate of inflation is 12% p. a. compounded annually, how much will this car cost in 5 years’ time? A =P(1 + i) A = 800 000(1, 1 2) A = R 1 409 873, 35

Example 2 You decide to invest R 50 000 now and you secure an interest rate of 9% p. a. compounded annually. The inflation rate is currently running at 12% p. a. (a) What will the future value of your money be in 15 years’ from now? (b) Due to inflation, what money will have the same buying power as R 50 000 in 15 years’ time? (c) By how much will the buying power of your money have declined after 15 years? (d) To what do you attribute this decline?

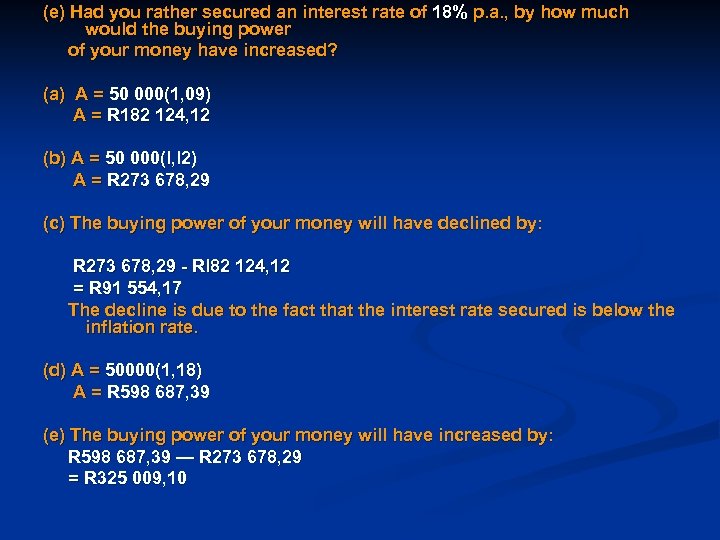(e) Had you rather secured an interest rate of 18% p. a. , by how much would the buying power of your money have increased? (a) A = 50 000(1, 09) A = R 182 124, 12 (b) A = 50 000(l, l 2) A = R 273 678, 29 (c) The buying power of your money will have declined by: R 273 678, 29 - Rl 82 124, 12 = R 91 554, 17 The decline is due to the fact that the interest rate secured is below the inflation rate. (d) A = 50000(1, 18) A = R 598 687, 39 (e) The buying power of your money will have increased by: R 598 687, 39 — R 273 678, 29 = R 325 009, 10

Example 2 Mabel is on a trip to England to visit her family. The current rand/pound exchange rate is R 12, 50 to the British pound. She has R 20 000 to spend in England. How many pounds does she have to spend in England? 1£ = R 12, 50 1£ divided by R 12, 50 £ 0, 08 = R 1 £ 0, 08 20 000 = R 1 20 000 £ 1600 = R 20 000 Mabel has £ 1600 to spend in England.

EXERCISE 5 1. 2. A DVD player costs $256 in California. What would it cost in South Africa if the Rand/dollar exchange rate is Rl 0, 45 to the US dollar? You want to buy a book online costing £ 35 in London. How much will it cost you in rand? The rand/pound exchange rate is RI 3 to the pound.

3. You want to buy a box of Japanese cigarettes costing 50 yen. (If the rand/yen exchange rate is one rand to 16, 78 yen) Calculate the cost of the sweets in rand. 4. Andrew is visiting a friend in New York for a week. He has R 2500 to spend and will exchange the money for US dollars. How many dollars will he have to spend if the rand/dollar exchange rate is R 10, 38 to the US dollar? 5. Sandesh wants to purchase an electric guitar from a music dealership in London. The guitar costs £ 3000 and Sandesh has saved R 40 000. The rand/pound exchange rate is R 13, 24 per one pound. Will he have enough money, in rand, to buy this guitar? Show your reasoning.

6. One yen costs R 0, 22. How much yen can you spend in Japan if you have R 3000 available to you? 7. A married couple living in England, having saved £ 4000, decided to visit the Kruger National Park in South Africa. The airfare cost £ 1100 and they converted the balance of their money into rand which they intended to spend in South Africa. They actually spent R 23000 in South Africa and converted their remaining rand back into pounds when they returned to England. The exchange rate on arrival in South Africa was R 14, 24 to the pound and R 12, 46 to the pound when they departed from South Africa. (a) How much, in rand, had the couple planned to spend in South Africa? (b) How many pounds did they take back to England? 8. A certain watch costs € 350 in Germany or £ 245 in England. Which price is better for the South African buyer if the exchange rates are R 9, 24 to the euro and R 12, 06 to the pound?