Module 11 The Utility-Maximizing Model 1 Objectives

Module 11 The Utility-Maximizing Model 1

Objectives v Use the utility-maximizing model to explain how consumers choose goods and services. 2

Objectives v Use the utility-maximizing model to explain how consumers choose goods and services. v Use the concept of utility to explain how the law of demand results from consumers adjusting their consumption choices to changes in prices. 3

Objective 1 Use the utility-maximizing model to explain how consumers choose goods and services v Be sure to understand the difference between total utility and marginal utility v Recall the law of diminishing marginal utility v Also know the terminology of this chapter, for example, terms such as “consumption bundle”, “consumer preferences. 4

Objective 1 Use the utility-maximizing model to explain how consumers choose goods and services v The goal of the utility-maximizing model is to derive the consumer’s demand curve v Economists assume that consumers try to allocate their limited incomes to maximize their satisfaction, a goal referred to as utility maximization 5

Objective 1 Use the utility-maximizing model to explain how consumers choose goods and services v The utility-maximizing model is used to determine the optimal amounts of goods and services a consumer will purchase given: 6

Objective 1 Use the utility-maximizing model to explain how consumers choose goods and services v The utility-maximizing model is used to determine the optimal amounts of goods and services a consumer will purchase given: Øknowledge of consumer’s preferences 7

Objective 1 Use the utility-maximizing model to explain how consumers choose goods and services v The utility-maximizing model is used to determine the optimal amounts of goods and services a consumer will purchase given: Øknowledge of consumer’s preferences Øthe prices of the goods and services 8

Objective 1 Use the utility-maximizing model to explain how consumers choose goods and services v The utility-maximizing model is used to determine the optimal amounts of goods and services a consumer will purchase given: Øknowledge of consumer’s preferences Øthe prices of the goods and services Øthe consumer’s budget constraint 9

Objective 1 Use the utility-maximizing model to explain how consumers choose goods and services v The consumer’s equilibrium bundle is a combination of goods and services consumed which gives the consumer the maximum total utility, subject to a budget constraint or an income constraint. v The terms “equilibrium” bundle, “optimal” bundle and “utility-maximizing” bundle are used interchangeably. 10

Objective 1: Using the utility-maximizing model v Suppose a consumer has $I to spend on two goods, X and Y. Let Px = price of good X and Py = price of good Y. 11

Objective 1: Using the utility-maximizing model v Suppose a consumer has $1 to spend on two goods, X and Y. Let Px = price of good X and Py = price of good Y. v How will the consumer allocate her $I towards these two goods so that she gets the most satisfaction? 12

Objective 1: Using the utility-maximizing model v Suppose a consumer has $1 to spend on two goods, X and Y. Let Px = price of good X and Py = price of good Y. v How will the consumer allocate her $1 towards these two goods so that she gets the most satisfaction? v The equilibrium bundle satisfies two conditions: 13

Objective 1: Using the utility-maximizing model v Suppose a consumer has $1 to spend on two goods, X and Y. Let Px = price of good X and Py = price of good Y. v How will the consumer allocate her $1 towards these two goods so that she gets the most satisfaction? v The equilibrium bundle satisfies two conditions: Condition 1: Income should be allocated so that the last dollar spent on each good yields the same amount of marginal utility. 14

Objective 1: Using the utility-maximizing model v The equilibrium bundle satisfies two conditions: Condition 1: Income should be allocated so that the last dollar spent on each good yields the same amount of marginal utility. In terms of an equation, where MU = marginal utility, and P = price, 15

Objective 1: Using the utility-maximizing model v The equilibrium bundle satisfies two conditions: Condition 1: Income should be allocated so that the last dollar spent on each good yields the same amount of marginal utility. In terms of an equation, where MU = marginal utility, and P = price, Marginal utility per dollar spent on good X Marginal utility per dollar spent on good Y 16

Objective 1: Using the utility-maximizing model Condition 2: The consumer must spend the total income allocated to the consumption of goods and services. 17

Objective 1: Using the utility-maximizing model Condition 2: The consumer must spend the total income allocated to the consumption of goods and services. In terms of an equation: Where and = Price of good X × Quantity of good X = expenditure on good X, = Price of good Y × Quantity of good Y = expenditure on good Y 18

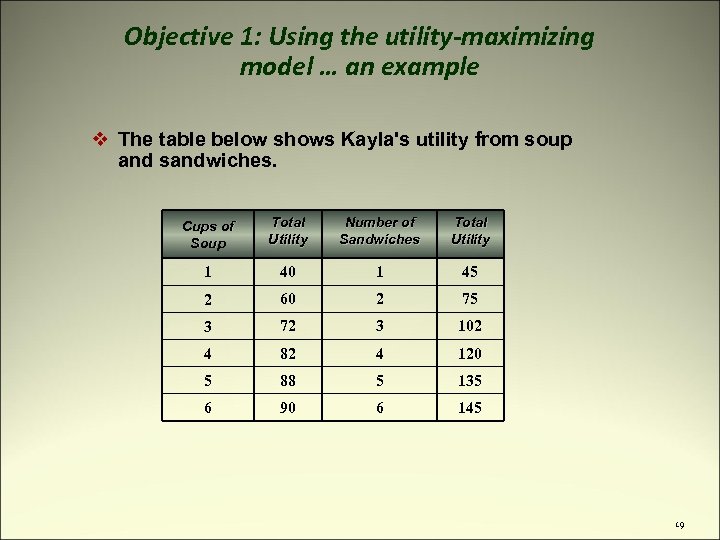
Objective 1: Using the utility-maximizing model … an example v The table below shows Kayla's utility from soup and sandwiches. Cups of Soup Total Utility Number of Sandwiches Total Utility 1 40 1 45 2 60 2 75 3 72 3 102 4 82 4 120 5 88 5 135 6 90 6 145 19

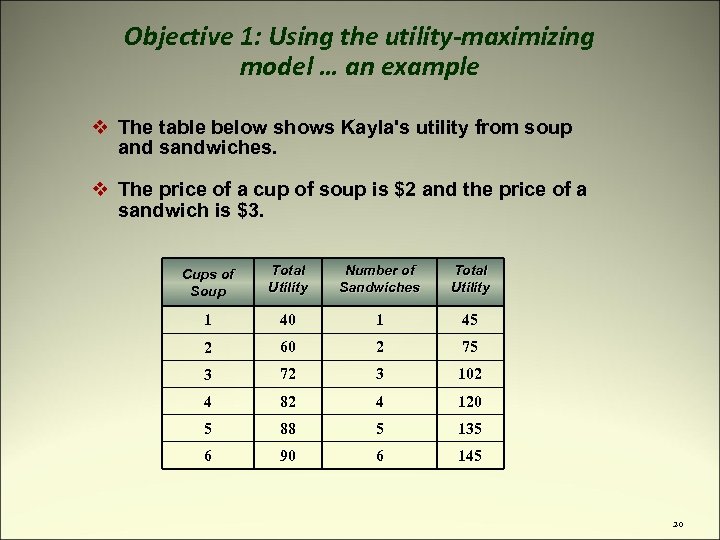
Objective 1: Using the utility-maximizing model … an example v The table below shows Kayla's utility from soup and sandwiches. v The price of a cup of soup is $2 and the price of a sandwich is $3. Cups of Soup Total Utility Number of Sandwiches Total Utility 1 40 1 45 2 60 2 75 3 72 3 102 4 82 4 120 5 88 5 135 6 90 6 145 20

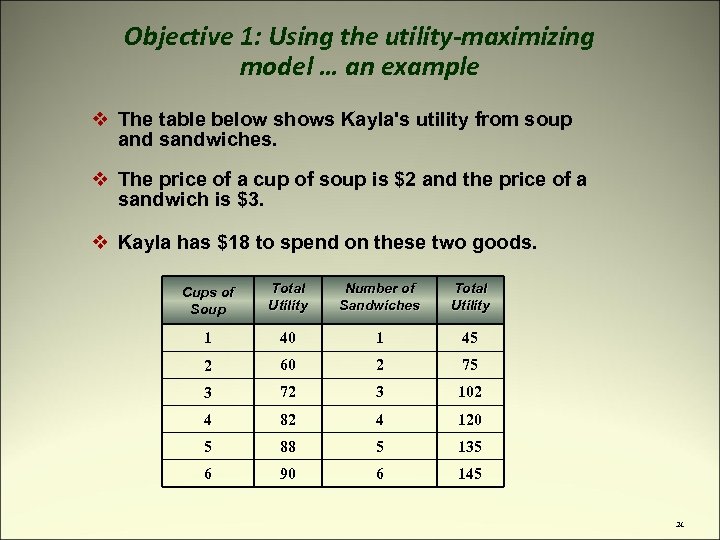
Objective 1: Using the utility-maximizing model … an example v The table below shows Kayla's utility from soup and sandwiches. v The price of a cup of soup is $2 and the price of a sandwich is $3. v Kayla has $18 to spend on these two goods. Cups of Soup Total Utility Number of Sandwiches Total Utility 1 40 1 45 2 60 2 75 3 72 3 102 4 82 4 120 5 88 5 135 6 90 6 145 21

Objective 1: … applying the utilitymaximizing conditions Step 1: Calculate the marginal utility per dollar spent on each good using the formula: marginal utility per dollar = marginal utility ÷ price of the good Note: To apply this step you must have marginal utility figures and the price of the product. If you are given total utility figures, you will have to calculate the marginal utility before using the equation above. 22

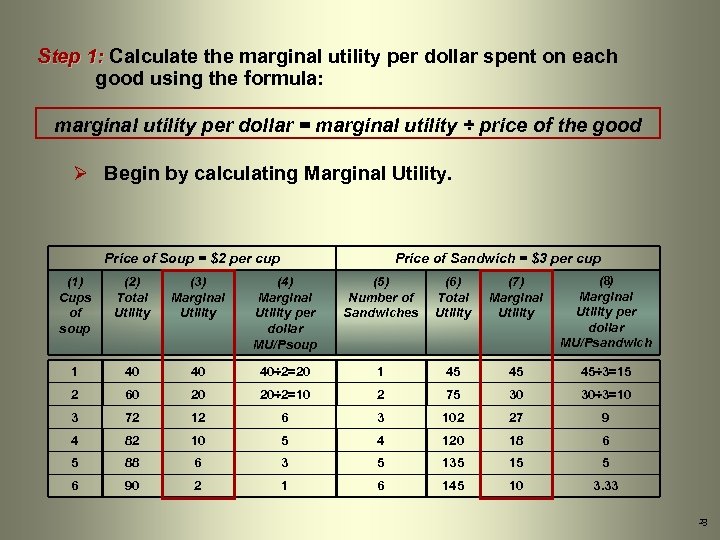
Step 1: Calculate the marginal utility per dollar spent on each good using the formula: marginal utility per dollar = marginal utility ÷ price of the good Ø Begin by calculating Marginal Utility. Price of Soup = $2 per cup Price of Sandwich = $3 per cup (8) (1) Cups of soup (2) Total Utility (3) Marginal Utility (4) Marginal Utility per dollar MU/Psoup (5) Number of Sandwiches (6) Total Utility (7) Marginal Utility 1 40 40 40÷ 2=20 1 45 45 45÷ 3=15 2 60 20 20÷ 2=10 2 75 30 30÷ 3=10 3 72 12 6 3 102 27 9 4 82 10 5 4 120 18 6 5 88 6 3 5 135 15 5 6 90 2 1 6 145 10 3. 33 Marginal Utility per dollar MU/Psandwich 23

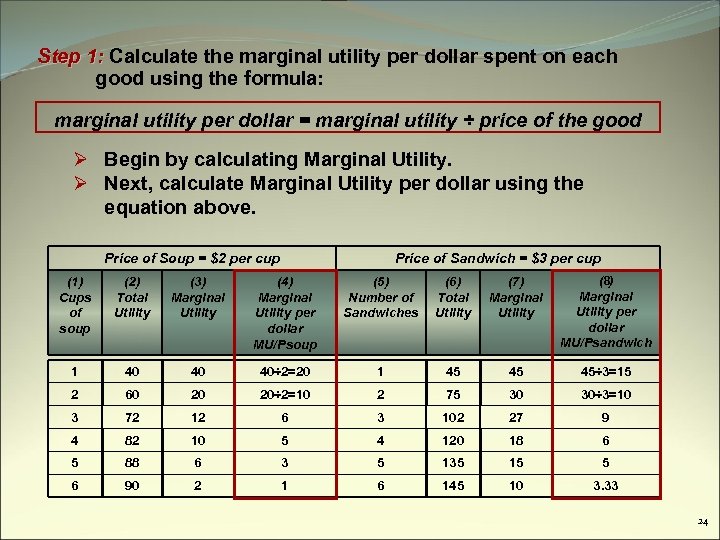
Step 1: Calculate the marginal utility per dollar spent on each good using the formula: marginal utility per dollar = marginal utility ÷ price of the good Ø Begin by calculating Marginal Utility. Ø Next, calculate Marginal Utility per dollar using the equation above. Price of Soup = $2 per cup Price of Sandwich = $3 per cup (8) (1) Cups of soup (2) Total Utility (3) Marginal Utility (4) Marginal Utility per dollar MU/Psoup (5) Number of Sandwiches (6) Total Utility (7) Marginal Utility 1 40 40 40÷ 2=20 1 45 45 45÷ 3=15 2 60 20 20÷ 2=10 2 75 30 30÷ 3=10 3 72 12 6 3 102 27 9 4 82 10 5 4 120 18 6 5 88 6 3 5 135 15 5 6 90 2 1 6 145 10 3. 33 Marginal Utility per dollar MU/Psandwich 24

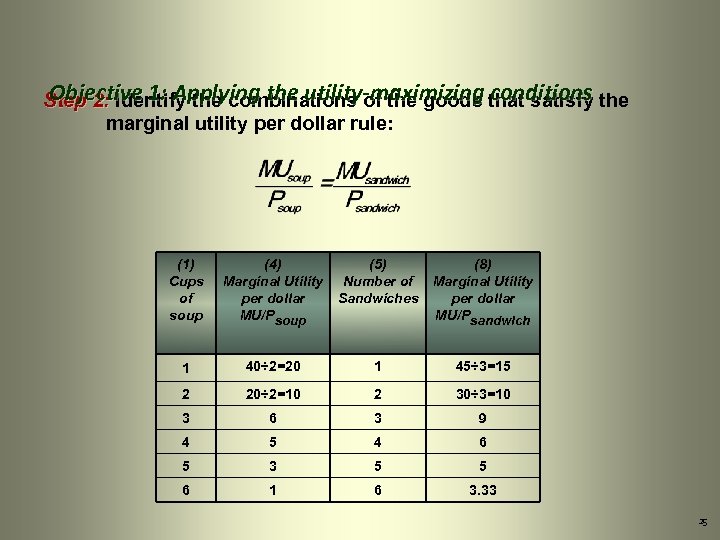
Objective 1: Applying the utility-maximizing conditions Step 2: Identify the combinations of the goods that satisfy the marginal utility per dollar rule: (1) Cups of soup (4) Marginal Utility per dollar MU/Psoup (5) Number of Sandwiches (8) Marginal Utility per dollar MU/Psandwich 1 40÷ 2=20 1 45÷ 3=15 2 20÷ 2=10 2 30÷ 3=10 3 6 3 9 4 5 4 6 5 3 5 5 6 1 6 3. 33 25

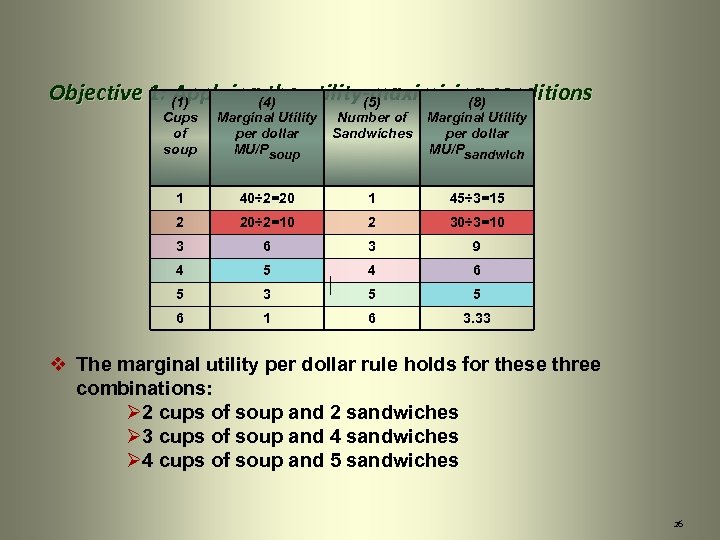
Objective 1: (1) Applying(4) utility-maximizing conditions the (5) (8) Cups of soup Marginal Utility per dollar MU/Psoup Number of Sandwiches Marginal Utility per dollar MU/Psandwich 1 40÷ 2=20 1 45÷ 3=15 2 20÷ 2=10 2 30÷ 3=10 3 6 3 9 4 5 4 6 5 3 5 5 6 1 6 3. 33 v The marginal utility per dollar rule holds for these three combinations: Ø 2 cups of soup and 2 sandwiches Ø 3 cups of soup and 4 sandwiches Ø 4 cups of soup and 5 sandwiches 26

Objective 1: Applying the utility-maximizing conditions Which of the three bundles is the optimal bundle? 27

Objective 1: Applying the utility-maximizing conditions Which of the three bundles is the optimal bundle? Step 3: Identify the optimal bundle by applying Condition 2: that Kayla’s expenditure on the two goods must exhaust her budget of $18. 28

Objective 1: Applying the utility-maximizing conditions Which of the three bundles is the optimal bundle? Step 3: Identify the optimal bundle by applying the condition 2: that Kayla’s expenditure on the two goods must exhaust her budget of $18. 2 cups of soup and 2 sandwiches will cost her $10 ($2× 2 cups of soup + $3× 2 sandwiches) 29

Objective 1: Applying the utility-maximizing conditions Which of the three bundles is the optimal bundle? Step 3: Identify the optimal bundle by applying the condition 2: that Kayla’s expenditure on the two goods must exhaust her budget of $18. 2 cups of soup and 2 sandwiches will cost her $10 ($2× 2 cups of soup + $3× 2 sandwiches) 3 cups of soup and 4 sandwiches will cost her $18 ($2× 3 cups of soup + $3× 4 sandwiches) 30

Objective 1: Applying the utility-maximizing conditions Which of the three bundles is the optimal bundle? Step 3: Identify the optimal bundle by applying the condition 2: that Kayla’s expenditure on the two goods must exhaust her budget of $18. 2 cups of soup and 2 sandwiches will cost her $10 ($2× 2 cups of soup + $3× 2 sandwiches) 3 cups of soup and 4 sandwiches will cost her $18 ($2× 3 cups of soup + $3× 4 sandwiches) 4 cups of soup and 5 sandwiches will cost her $23 ($2× 4 cups of soup + $3× 5 sandwiches) 31

Objective 1: Applying the utility-maximizing conditions Which of the three bundles is the optimal bundle? Step 3: Identify the optimal bundle by applying the condition 2: that Kayla’s expenditure on the two goods must exhaust her budget of $18. 2 cups of soup and 2 sandwiches will cost her $10 ($2× 2 cups of soup + $3× 2 sandwiches) 3 cups of soup and 4 sandwiches will cost her $18 ($2× 3 cups of soup + $3× 4 sandwiches) 4 cups of soup and 5 sandwiches will cost her $23 ($2× 4 cups of soup + $3× 5 sandwiches) Kayla’s equilibrium bundle is 3 cups of soup and 4 sandwiches. 32

Objective 1: … the utility-maximizing model v The utility maximizing model applies a key economic principle: optimal decisions are made at the margin. 33

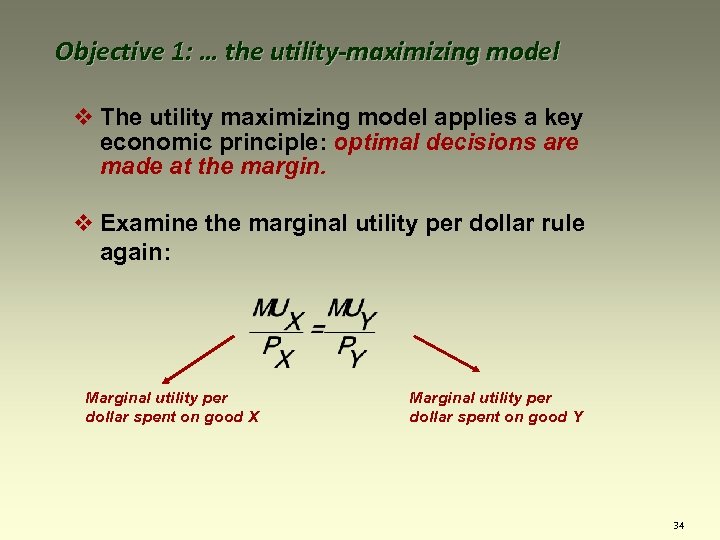
Objective 1: … the utility-maximizing model v The utility maximizing model applies a key economic principle: optimal decisions are made at the margin. v Examine the marginal utility per dollar rule again: Marginal utility per dollar spent on good X Marginal utility per dollar spent on good Y 34

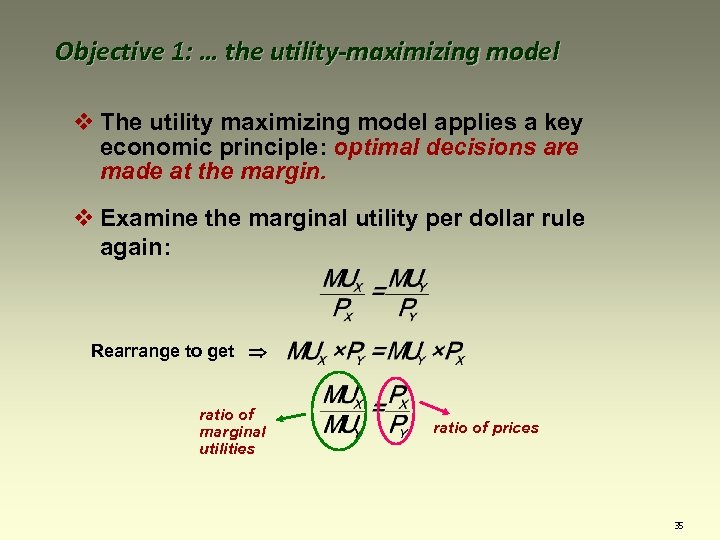
Objective 1: … the utility-maximizing model v The utility maximizing model applies a key economic principle: optimal decisions are made at the margin. v Examine the marginal utility per dollar rule again: Rearrange to get ratio of marginal utilities ratio of prices 35

Objective 1: … the utility-maximizing model v Examine the marginal utility per dollar rule: Rearrange to get ratio of prices is also called relative prices v What is the meaning of relative prices? Suppose, where X=soup and Y=sandwich, then Kayla must give up 2/3 of a sandwich (Y) for I more cup of soup (X). v The relative price is the opportunity cost of consuming 1 more unit of X or the market dictated rate of exchange between good X and good Y. 36

Objective 1: … the utility-maximizing model v Examine the marginal utility per dollar rule: Rearrange to get Ratio of marginal utilities also called the marginal rate of substitution ratio of prices is also called relative prices v What is the ratio of marginal utilities? v The ratio of marginal utilities is also called the marginal rate of substitution v It shows the rate at which the consumer is willing to give up some of good Y (sandwich) for an additional unit of good X (soup). In other words, it is a measure of the consumer’s subjective or personal rate of exchange. 37

Objective 1: … the utility-maximizing model v Examine the marginal utility per dollar rule: Rearrange to get ratio of marginal utilities also called the marginal rate of substitution ratio of prices is also called relative prices v In equilibrium, the consumer’s subjective rate of exchange (ratio of marginal utilities) equals the rate of exchange required by the market (ratio of prices). 38

Objective 2 Use the concept of utility to explain how the law of demand results … v An individual’s utility-maximizing choices lead to a demand curve. v Recall, that the demand curve shows the quantities demanded at alternative prices v The utility-maximizing consumer adjusts her consumption choices to changes in prices. 39

Objective 2 Use the utility maximizing model to derive a demand curve v To derive Kayla’s demand for sandwiches curve, we must change the price of sandwiches and observe what happens to her quantity demanded of sandwiches, holding all else constant. 40

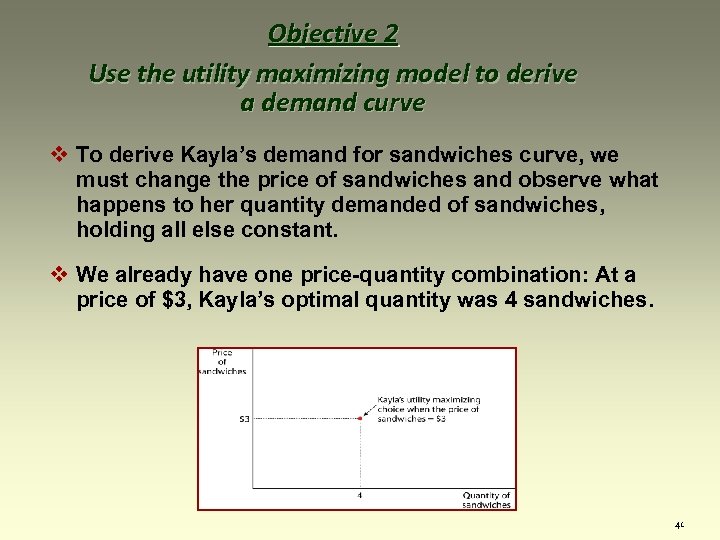
Objective 2 Use the utility maximizing model to derive a demand curve v To derive Kayla’s demand for sandwiches curve, we must change the price of sandwiches and observe what happens to her quantity demanded of sandwiches, holding all else constant. v We already have one price-quantity combination: At a price of $3, Kayla’s optimal quantity was 4 sandwiches. 41

Objective 2: … deriving a demand curve. v To construct a demand curve we need at least one other price-quantity combination. 42

Objective 2: … deriving a demand curve. v To construct a demand curve we need at least one other price-quantity combination. v Suppose the price of sandwiches rises to $4. 00. How would Kayla’s quantity demanded of sandwiches change? 43

Objective 2: … deriving a demand curve. v To construct a demand curve we need at least one other price-quantity combination. v Suppose the price of sandwiches rises to $4. 00. How would Kayla’s quantity demanded of sandwiches change? v Since the price of one good has changed we have to recalculate the marginal utility per dollar for that good. 44

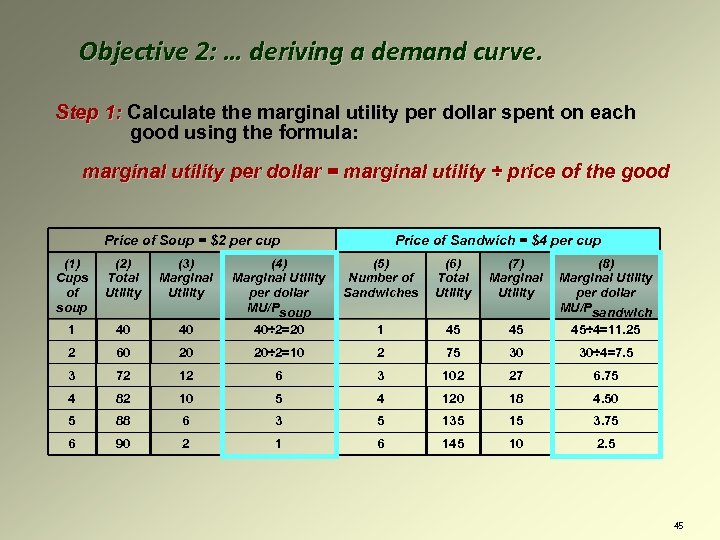
Objective 2: … deriving a demand curve. Step 1: Calculate the marginal utility per dollar spent on each good using the formula: marginal utility per dollar = marginal utility ÷ price of the good Price of Soup = $2 per cup Price of Sandwich = $4 per cup (1) Cups of soup (2) Total Utility (3) Marginal Utility (4) Marginal Utility per dollar MU/Psoup (5) Number of Sandwiches (6) Total Utility (7) Marginal Utility (8) Marginal Utility per dollar MU/Psandwich 1 40 40 40÷ 2=20 1 45 45 45÷ 4=11. 25 2 60 20 20÷ 2=10 2 75 30 30÷ 4=7. 5 3 72 12 6 3 102 27 6. 75 4 82 10 5 4 120 18 4. 50 5 88 6 3 5 135 15 3. 75 6 90 2 1 6 145 10 2. 5 45

Objective 2: … deriving a demand curve. v How to determine the optimal combination of soup and sandwiches in the case where the rule of equal marginal utility per dollar does not hold? 46

Objective 2: … deriving a demand curve. v How to determine the optimal combination of soup and sandwiches in the case where the rule of equal marginal utility per dollar does not hold? v Apply the principle of marginal analysis. Ask the question: what is the first item Kayla should buy? 47

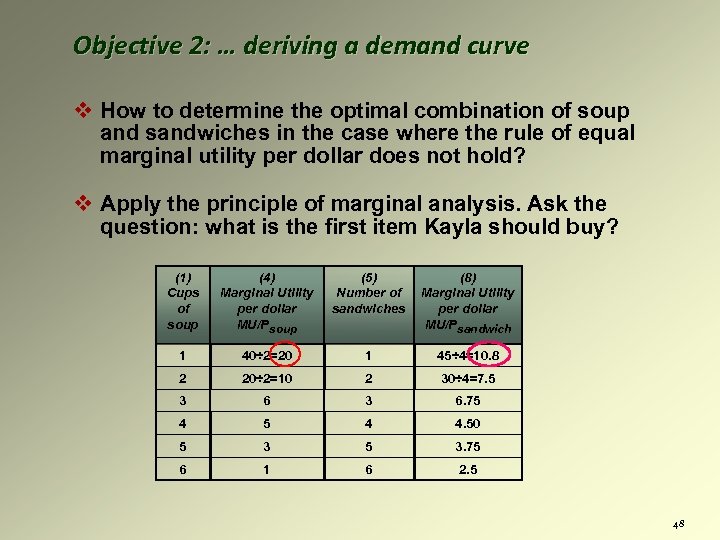
Objective 2: … deriving a demand curve v How to determine the optimal combination of soup and sandwiches in the case where the rule of equal marginal utility per dollar does not hold? v Apply the principle of marginal analysis. Ask the question: what is the first item Kayla should buy? (1) Cups of soup (4) Marginal Utility per dollar MU/Psoup (5) Number of sandwiches (8) Marginal Utility per dollar MU/Psandwich 1 40÷ 2=20 1 45÷ 4=10. 8 2 20÷ 2=10 2 30÷ 4=7. 5 3 6. 75 4 4. 50 5 3. 75 6 1 6 2. 5 48

Objective 2: … deriving a demand curve v Obviously, the item that gives her the highest marginal utility per dollar spent. What is the 2 nd item? … and so forth until her budget is exhausted. (1) Cups of soup (4) Marginal Utility per dollar MU/Psoup (5) Number of Sandwiches (8) Marginal Utility per dollar MU/Psandwich Goods consumed Budget = $18 1 40÷ 2 = 20 1 45÷ 4 = 10. 8 1 st cup of soup $18 -$2 =$16 2 20÷ 2 = 10 2 30÷ 4 = 7. 5 1 st sandwich $16 -$4 =$12 3 6. 75 2 nd cup of soup $12 -$2 =$10 4 5 4 4. 50 2 nd sandwich $10 -$4=$6 5 3. 75 3 rd sandwich $6 -$4 =$2 6 1 6 2. 5 3 rd cup of soup $2 -$2 =$0 49

Objective 2: … deriving a demand curve v Obviously, the item that gives her the highest marginal utility per dollar spent. What is the 2 nd item? … and so forth until her budget is exhausted. (1) Cups of soup (4) Marginal Utility per dollar MU/Psoup (5) Number of Sandwiches (8) Marginal Utility per dollar MU/Psandwich Goods consumed Budget = $18 1 40÷ 2 = 20 1 45÷ 4 = 10. 8 1 st cup of soup $18 -$2 =$16 2 20÷ 2 = 10 2 30÷ 4 = 7. 5 1 st sandwich $16 -$4 =$12 3 6. 75 2 nd cup of soup $12 -$2 =$10 4 5 4 4. 50 2 nd sandwich $10 -$4=$6 5 3. 75 3 rd sandwich $6 -$4 =$2 6 1 6 2. 5 3 rd cup of soup $2 -$2 =$0 v Her utility maximizing bundle is 3 cups of soup and 3 sandwiches. 50

Objective 2: … deriving a demand curve v Now that we have two price-quantity combination points on Kayla’s demand for sandwiches curve we can trace her demand curve. 51

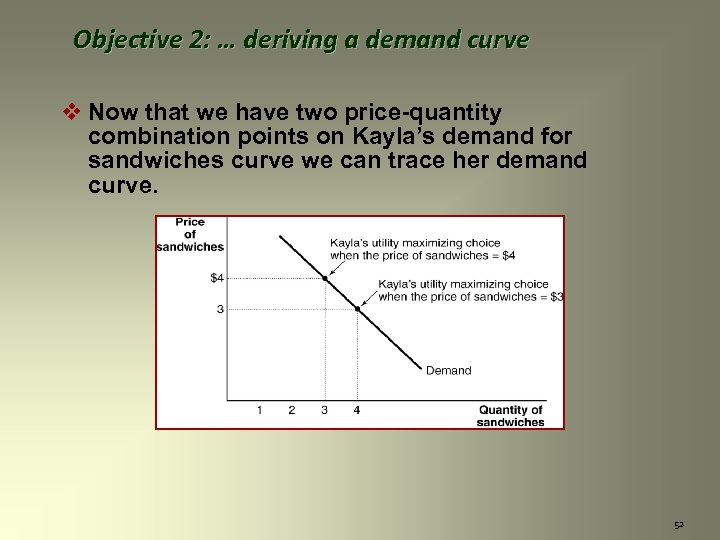
Objective 2: … deriving a demand curve v Now that we have two price-quantity combination points on Kayla’s demand for sandwiches curve we can trace her demand curve. 52

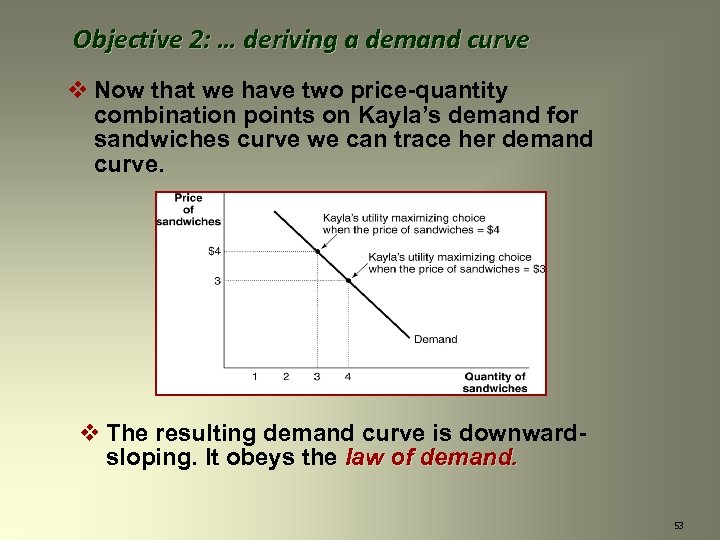
Objective 2: … deriving a demand curve v Now that we have two price-quantity combination points on Kayla’s demand for sandwiches curve we can trace her demand curve. v The resulting demand curve is downwardsloping. It obeys the law of demand. 53

Key Points v The utility-maximizing choices lead to a demand curve. Each price-quantity combination on a demand curve is a utility-maximizing quantity, quantity given the price. 54

Key Points v The utility-maximizing choices lead to a demand curve. Each price-quantity combination on a demand curve is a utility-maximizing quantity, quantity given the price. v If people seek to maximize utility, then the law of demand follows. 55

Key Points v When price changes, there a substitution effect and an income effect on the quantity of the good demanded. Ø The substitution effect of a price change is the change in quantity demanded that results from a change in price, making the good more of less expensive relative to other goods (that can substitute for it), holding purchasing power constant. Ø The income effect of a price change is the change in quantity demanded that results from the effect of the price change on the consumer’s purchasing power, all else constant. 56

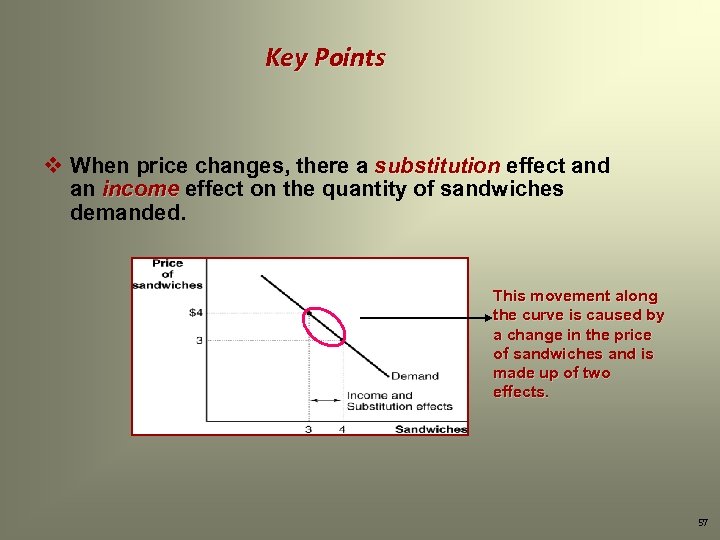
Key Points v When price changes, there a substitution effect and an income effect on the quantity of sandwiches demanded. This movement along the curve is caused by a change in the price of sandwiches and is made up of two effects. 57

Objective 2: … how a consumer adjusts to a price change v Initially, when the price of soup = $2 and the price of sandwich = $3, Kayla’s equilibrium bundle was 3 cups of soup and 4 sandwiches. 58

Objective 2: … how a consumer adjusts to a price change v Initially, when the price of soup = $2 and the price of sandwich = $3, Kayla’s equilibrium bundle was 3 cups of soup and 4 sandwiches. v The ratio of marginal utility to price was the same for soup and for sandwiches. 59

Objective 2: … how a consumer adjusts to a price change v Initially, when the price of soup = $2 and the price of sandwich = $3, Kayla’s equilibrium bundle was 3 cups of soup and 4 sandwiches. v The ratio of marginal utility to price was the same for soup and for sandwiches. v When a consumer is in equilibrium, she is maximizing utility. 60

Objective 2: … how a consumer adjusts to a price change v When the price of sandwiches rises to $4, the ratios of marginal utility to price no longer hold with equality. 61

Objective 2: … how a consumer adjusts to a price change v When the price of sandwiches rises to $4, the ratios of marginal utility to price no longer hold with equality. v We now have: A dollar spent on soup gives Kayla more utility than a dollar spent on sandwiches 62

Objective 2: … how a consumer adjusts to a price change A dollar spent on soup gives Kayla more utility than a dollar spent on sandwiches v To restore equilibrium, Kayla buys more soup and fewer sandwiches, subject to her budget constraint. 63

Objective 2: … how a consumer adjusts to a price change A dollar spent on soup gives Kayla more utility than a dollar spent on sandwiches v To restore equilibrium, Kayla buys more soup and fewer sandwiches, subject to her budget constraint. v In my example, given her budget, Kayla buys fewer sandwiches but is not able to increase her soup consumption. 64

Objective 2: … how a consumer adjusts to a price change A dollar spent on soup gives Kayla more utility than a dollar spent on sandwiches v To restore equilibrium, Kayla buys more soup and fewer sandwiches, subject to her budget constraint. v In my example, given her budget, Kayla buys fewer sandwiches but is not able to increase her soup consumption. v Note that when the price of sandwiches rises, quantity demanded falls – a result consistent with the law of demand. 65

End of Module 11 The Utility-Maximizing Model Song: Album: Artist: Material Girl Like a Virgin Madonna 66