1d84af94fc980a995b11ebaad4fab248.ppt
- Количество слайдов: 141
 MODULE 1 CHANGES IN QUANTITIES, CONSTANT RATE OF CHANGE, AND LINEAR FUNCTIONS Part 1: Investigations #1 -5 Investigation #1: Reasoning with Quantities Investigation #2: Changes in Quantities’ Values Investigation #3: Constant Rate of Change Investigation #4: Practice with Constant Rate of Change Investigation #5: Applying Constant Rate of Change to Find New Values Copyright © 2013 Carlson, O’Bryan, & Joyner 1
MODULE 1 CHANGES IN QUANTITIES, CONSTANT RATE OF CHANGE, AND LINEAR FUNCTIONS Part 1: Investigations #1 -5 Investigation #1: Reasoning with Quantities Investigation #2: Changes in Quantities’ Values Investigation #3: Constant Rate of Change Investigation #4: Practice with Constant Rate of Change Investigation #5: Applying Constant Rate of Change to Find New Values Copyright © 2013 Carlson, O’Bryan, & Joyner 1
 I#1 REASONING WITH QUANTITIES Quantity A quantity is some attribute of an object that you can imagine as being measured. Examples: i) your height ii) the number of people in this room iii) the amount of money in your pocket iv) the distance around a 400 -meter track Copyright © 2013 Carlson, O’Bryan, & Joyner 2
I#1 REASONING WITH QUANTITIES Quantity A quantity is some attribute of an object that you can imagine as being measured. Examples: i) your height ii) the number of people in this room iii) the amount of money in your pocket iv) the distance around a 400 -meter track Copyright © 2013 Carlson, O’Bryan, & Joyner 2
 I#1 1. Sarah decides to ride a Ferris wheel at a local fair. The animation shown models her ride around the Ferris wheel. Assume she is seated in the brown cart and starts at the bottom of the Ferris wheel. Watch the Ferris wheel animation as Sarah rotates around twice and then respond to the following questions. Choose one of the following links to load a Ferris wheel applet. Ferris Wheel 1 (requires HTML 5) Rational Reasoning applet. This is a better option, but may require a browser upgrade. Ferris Wheel 2 Applet designed by another group. Copyright © 2013 Carlson, O’Bryan, & Joyner 3
I#1 1. Sarah decides to ride a Ferris wheel at a local fair. The animation shown models her ride around the Ferris wheel. Assume she is seated in the brown cart and starts at the bottom of the Ferris wheel. Watch the Ferris wheel animation as Sarah rotates around twice and then respond to the following questions. Choose one of the following links to load a Ferris wheel applet. Ferris Wheel 1 (requires HTML 5) Rational Reasoning applet. This is a better option, but may require a browser upgrade. Ferris Wheel 2 Applet designed by another group. Copyright © 2013 Carlson, O’Bryan, & Joyner 3
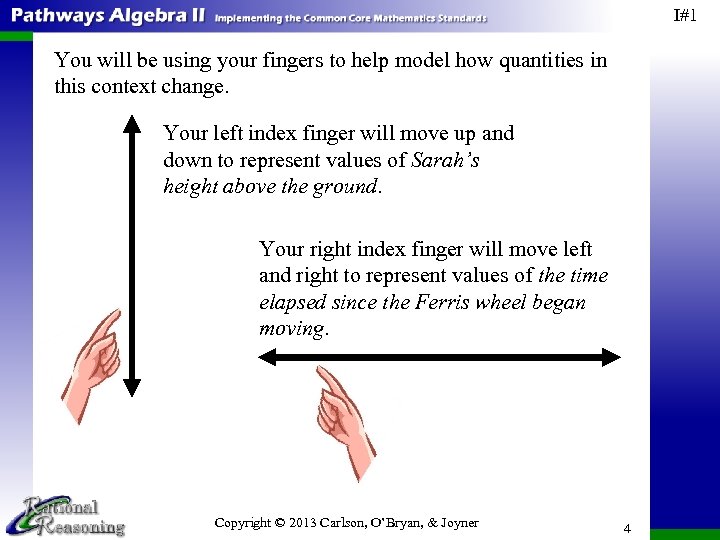 I#1 You will be using your fingers to help model how quantities in this context change. Your left index finger will move up and down to represent values of Sarah’s height above the ground. Your right index finger will move left and right to represent values of the time elapsed since the Ferris wheel began moving. Copyright © 2013 Carlson, O’Bryan, & Joyner 4
I#1 You will be using your fingers to help model how quantities in this context change. Your left index finger will move up and down to represent values of Sarah’s height above the ground. Your right index finger will move left and right to represent values of the time elapsed since the Ferris wheel began moving. Copyright © 2013 Carlson, O’Bryan, & Joyner 4
 I#1 1. Sarah decides to ride a Ferris wheel at a local fair. The animation shown models her ride around the Ferris wheel. Assume she is seated in the brown cart and starts at the bottom of the Ferris wheel. Watch the Ferris wheel animation as Sarah rotates around twice and then respond to the following questions. a. What varying quantities can you identify in this situation? Answers may vary. Some possibilities include • Sarah’s distance above the ground • Sarah’s distance from different carts • The elapsed time since the Ferris wheel began moving • etc. Copyright © 2013 Carlson, O’Bryan, & Joyner 5
I#1 1. Sarah decides to ride a Ferris wheel at a local fair. The animation shown models her ride around the Ferris wheel. Assume she is seated in the brown cart and starts at the bottom of the Ferris wheel. Watch the Ferris wheel animation as Sarah rotates around twice and then respond to the following questions. a. What varying quantities can you identify in this situation? Answers may vary. Some possibilities include • Sarah’s distance above the ground • Sarah’s distance from different carts • The elapsed time since the Ferris wheel began moving • etc. Copyright © 2013 Carlson, O’Bryan, & Joyner 5
 I#1 b. How does Sarah’s height above the ground vary? Initially, Sarah’s height above the ground increases, then after reaching the top of the Ferris wheel her height above the ground decreases until she returns to her starting location. The pattern then repeats. c. How does the time since the Ferris wheel began moving vary? As the animation runs, the time since the Ferris wheel began moving increases. Copyright © 2013 Carlson, O’Bryan, & Joyner 6
I#1 b. How does Sarah’s height above the ground vary? Initially, Sarah’s height above the ground increases, then after reaching the top of the Ferris wheel her height above the ground decreases until she returns to her starting location. The pattern then repeats. c. How does the time since the Ferris wheel began moving vary? As the animation runs, the time since the Ferris wheel began moving increases. Copyright © 2013 Carlson, O’Bryan, & Joyner 6
 I#1 d. How do the quantities time since the Ferris wheel began moving and Sarah’s height above the ground vary together? As the time since the Ferris wheel began moving increases, Sarah’s height above the ground initially increases and then decreases. The pattern then repeats as the time since the Ferris wheel began moving continues to increase. Copyright © 2013 Carlson, O’Bryan, & Joyner 7
I#1 d. How do the quantities time since the Ferris wheel began moving and Sarah’s height above the ground vary together? As the time since the Ferris wheel began moving increases, Sarah’s height above the ground initially increases and then decreases. The pattern then repeats as the time since the Ferris wheel began moving continues to increase. Copyright © 2013 Carlson, O’Bryan, & Joyner 7
 I#1 Points and Graphs A point shows the corresponding values of two quantities that we are comparing. A graph of the relationship between the two quantities is a collection of points showing all pairs of corresponding values. 2 a. The given axes are labeled time since the Ferris wheel began moving and Sarah’s height above the ground. Your teacher will play the animation again while you represent how these quantities are changing together using your fingers. Each time the video stops, plot a point on the axes that represents the corresponding values of time since the Ferris wheel began moving and Sarah’s height above ground. Copyright © 2013 Carlson, O’Bryan, & Joyner 8
I#1 Points and Graphs A point shows the corresponding values of two quantities that we are comparing. A graph of the relationship between the two quantities is a collection of points showing all pairs of corresponding values. 2 a. The given axes are labeled time since the Ferris wheel began moving and Sarah’s height above the ground. Your teacher will play the animation again while you represent how these quantities are changing together using your fingers. Each time the video stops, plot a point on the axes that represents the corresponding values of time since the Ferris wheel began moving and Sarah’s height above ground. Copyright © 2013 Carlson, O’Bryan, & Joyner 8
 I#1 Copyright © 2013 Carlson, O’Bryan, & Joyner 9
I#1 Copyright © 2013 Carlson, O’Bryan, & Joyner 9
 I#1 A graph of the relationship between the two quantities is really a collection of points. Each point tells us the corresponding values of two quantities that we are comparing. Copyright © 2013 Carlson, O’Bryan, & Joyner 10
I#1 A graph of the relationship between the two quantities is really a collection of points. Each point tells us the corresponding values of two quantities that we are comparing. Copyright © 2013 Carlson, O’Bryan, & Joyner 10
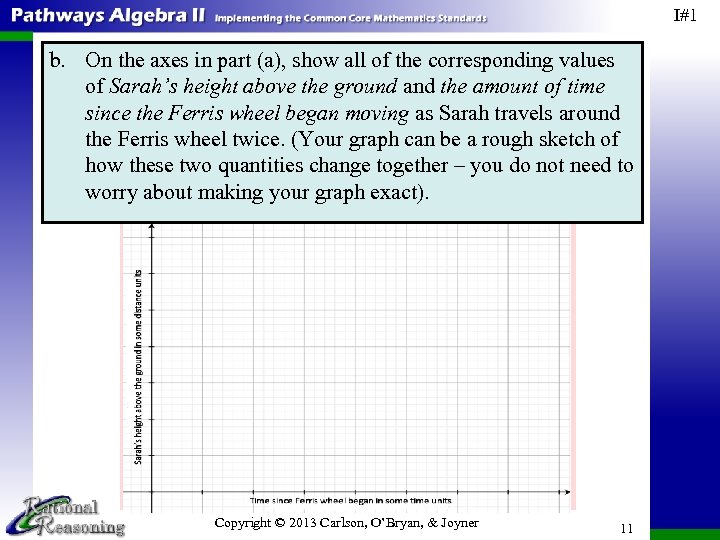 I#1 b. On the axes in part (a), show all of the corresponding values of Sarah’s height above the ground and the amount of time since the Ferris wheel began moving as Sarah travels around the Ferris wheel twice. (Your graph can be a rough sketch of how these two quantities change together – you do not need to worry about making your graph exact). Copyright © 2013 Carlson, O’Bryan, & Joyner 11
I#1 b. On the axes in part (a), show all of the corresponding values of Sarah’s height above the ground and the amount of time since the Ferris wheel began moving as Sarah travels around the Ferris wheel twice. (Your graph can be a rough sketch of how these two quantities change together – you do not need to worry about making your graph exact). Copyright © 2013 Carlson, O’Bryan, & Joyner 11
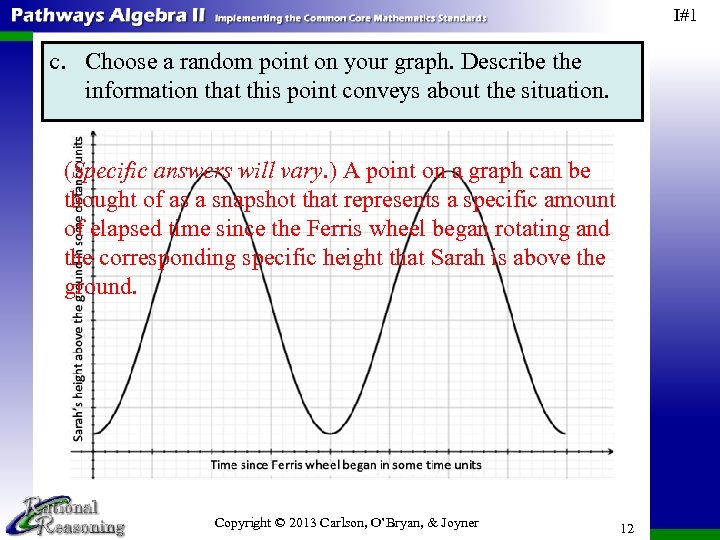 I#1 c. Choose a random point on your graph. Describe the information that this point conveys about the situation. (Specific answers will vary. ) A point on a graph can be thought of as a snapshot that represents a specific amount of elapsed time since the Ferris wheel began rotating and the corresponding specific height that Sarah is above the ground. Copyright © 2013 Carlson, O’Bryan, & Joyner 12
I#1 c. Choose a random point on your graph. Describe the information that this point conveys about the situation. (Specific answers will vary. ) A point on a graph can be thought of as a snapshot that represents a specific amount of elapsed time since the Ferris wheel began rotating and the corresponding specific height that Sarah is above the ground. Copyright © 2013 Carlson, O’Bryan, & Joyner 12
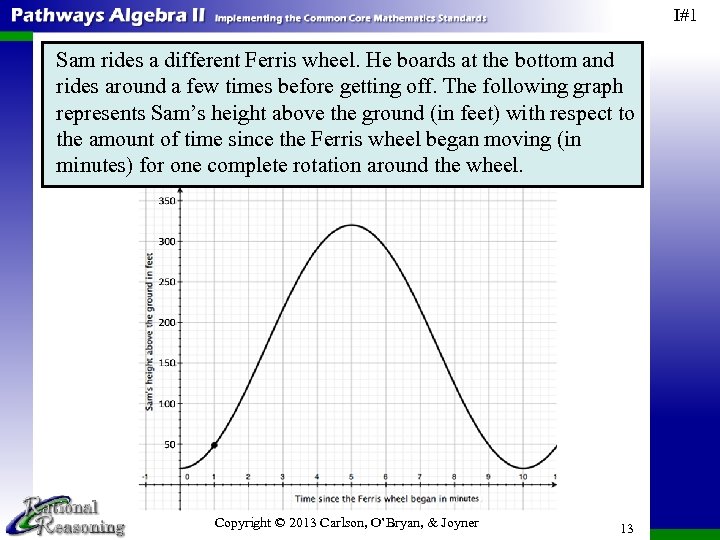 I#1 Sam rides a different Ferris wheel. He boards at the bottom and rides around a few times before getting off. The following graph represents Sam’s height above the ground (in feet) with respect to the amount of time since the Ferris wheel began moving (in minutes) for one complete rotation around the wheel. Copyright © 2013 Carlson, O’Bryan, & Joyner 13
I#1 Sam rides a different Ferris wheel. He boards at the bottom and rides around a few times before getting off. The following graph represents Sam’s height above the ground (in feet) with respect to the amount of time since the Ferris wheel began moving (in minutes) for one complete rotation around the wheel. Copyright © 2013 Carlson, O’Bryan, & Joyner 13
 I#1 3. The point (1, 50) is plotted on the graph. Explain what information this point conveys in the context of the problem. 1 minute after the Ferris wheel began moving, Sam was 50 feet above the ground. 4 a. How much did the time since the Ferris wheel began moving change from 1 to 4 minutes? The time since the Ferris wheel began moving changed by 3 minutes, from 1 second elapsed to 4 minutes elapsed, and we can calculate this change with the expression 4 – 1 = 3. Basically we are asking for the change in time that satisfies (1 minute elapsed) + (what change in time? ) = 4 minutes elapsed. Copyright © 2013 Carlson, O’Bryan, & Joyner 14
I#1 3. The point (1, 50) is plotted on the graph. Explain what information this point conveys in the context of the problem. 1 minute after the Ferris wheel began moving, Sam was 50 feet above the ground. 4 a. How much did the time since the Ferris wheel began moving change from 1 to 4 minutes? The time since the Ferris wheel began moving changed by 3 minutes, from 1 second elapsed to 4 minutes elapsed, and we can calculate this change with the expression 4 – 1 = 3. Basically we are asking for the change in time that satisfies (1 minute elapsed) + (what change in time? ) = 4 minutes elapsed. Copyright © 2013 Carlson, O’Bryan, & Joyner 14
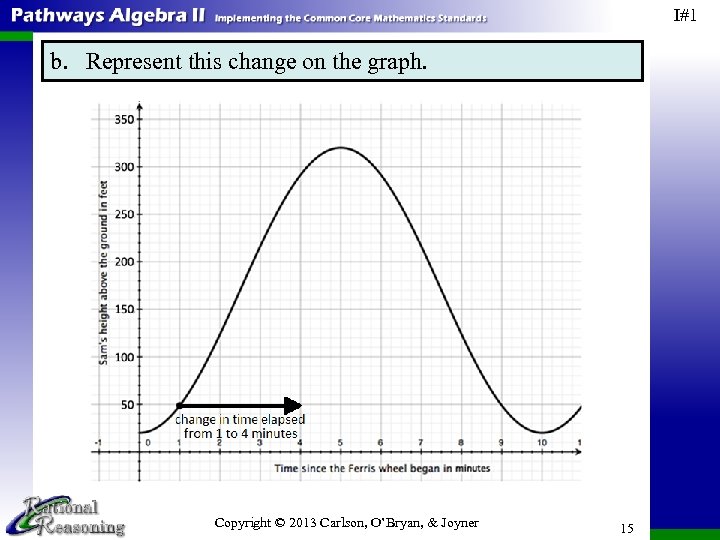 I#1 b. Represent this change on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 15
I#1 b. Represent this change on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 15
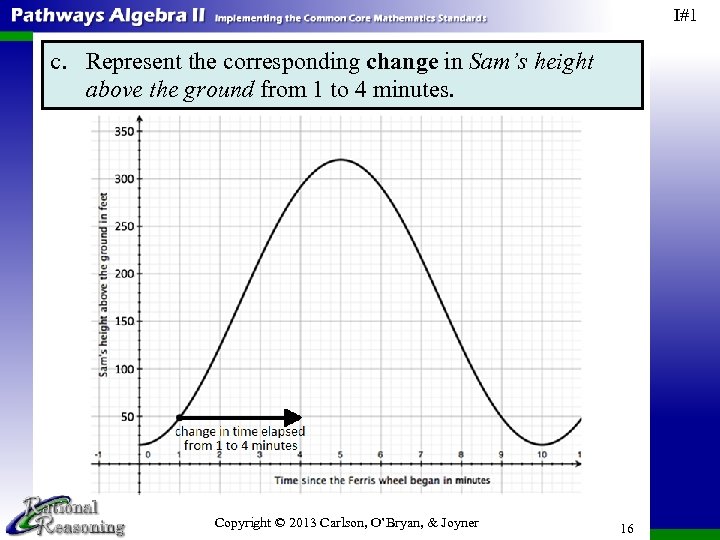 I#1 c. Represent the corresponding change in Sam’s height above the ground from 1 to 4 minutes. Copyright © 2013 Carlson, O’Bryan, & Joyner 16
I#1 c. Represent the corresponding change in Sam’s height above the ground from 1 to 4 minutes. Copyright © 2013 Carlson, O’Bryan, & Joyner 16
 I#1 d. Approximately how much did Sam’s height above the ground change over this time interval? Explain how you determined the change. This change is represented by the length of the vertical line segment drawn in part (c) and is approximately 240 feet. Estimates may vary slightly. e. Approximately how much did Sam’s height above the ground change over this time interval? Explain how you determined the change. Sam is about 290 feet above the ground 4 minutes after the Ferris wheel began moving. Estimates and methods may vary. Copyright © 2013 Carlson, O’Bryan, & Joyner 17
I#1 d. Approximately how much did Sam’s height above the ground change over this time interval? Explain how you determined the change. This change is represented by the length of the vertical line segment drawn in part (c) and is approximately 240 feet. Estimates may vary slightly. e. Approximately how much did Sam’s height above the ground change over this time interval? Explain how you determined the change. Sam is about 290 feet above the ground 4 minutes after the Ferris wheel began moving. Estimates and methods may vary. Copyright © 2013 Carlson, O’Bryan, & Joyner 17
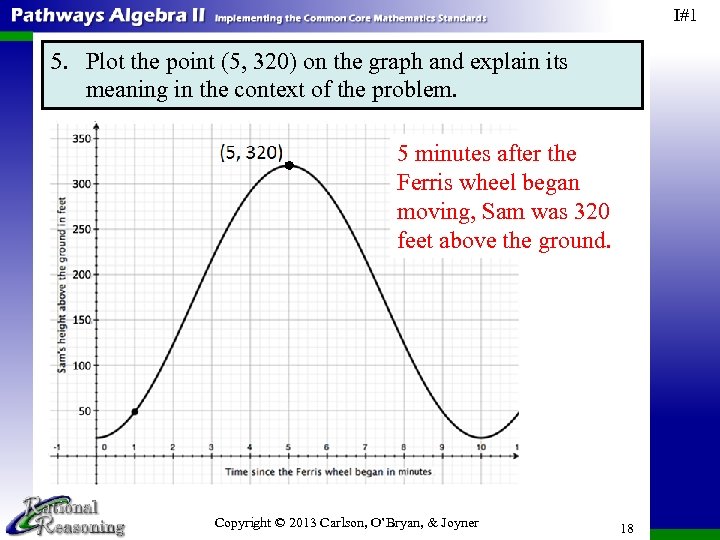 I#1 5. Plot the point (5, 320) on the graph and explain its meaning in the context of the problem. 5 minutes after the Ferris wheel began moving, Sam was 320 feet above the ground. Copyright © 2013 Carlson, O’Bryan, & Joyner 18
I#1 5. Plot the point (5, 320) on the graph and explain its meaning in the context of the problem. 5 minutes after the Ferris wheel began moving, Sam was 320 feet above the ground. Copyright © 2013 Carlson, O’Bryan, & Joyner 18
 I#1 6 a. How much did the time since the Ferris wheel began moving change from 5 to 7 minutes? The time since the Ferris wheel began moving changed by 2 minutes, from 5 minutes elapsed to 7 minutes elapsed. We can calculate this change with the expression 7 – 5 = 2. Basically we are asking for the change in time that satisfies (5 minutes elapsed) + (what change in time? ) = 7 minutes elapsed. Copyright © 2013 Carlson, O’Bryan, & Joyner 19
I#1 6 a. How much did the time since the Ferris wheel began moving change from 5 to 7 minutes? The time since the Ferris wheel began moving changed by 2 minutes, from 5 minutes elapsed to 7 minutes elapsed. We can calculate this change with the expression 7 – 5 = 2. Basically we are asking for the change in time that satisfies (5 minutes elapsed) + (what change in time? ) = 7 minutes elapsed. Copyright © 2013 Carlson, O’Bryan, & Joyner 19
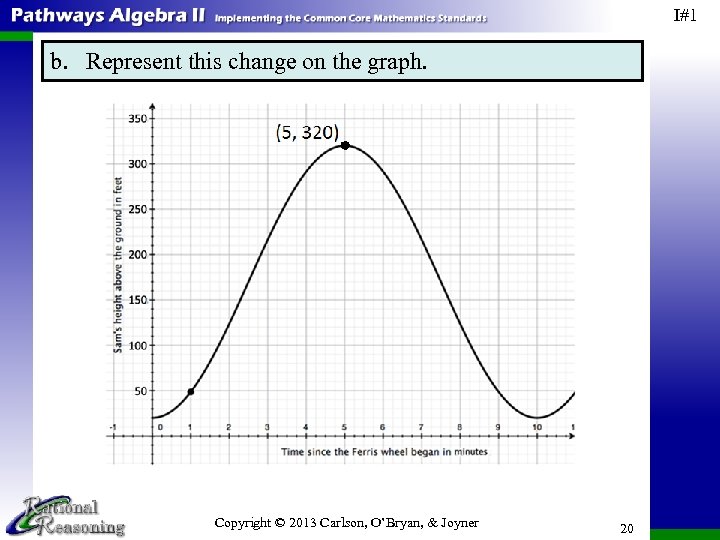 I#1 b. Represent this change on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 20
I#1 b. Represent this change on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 20
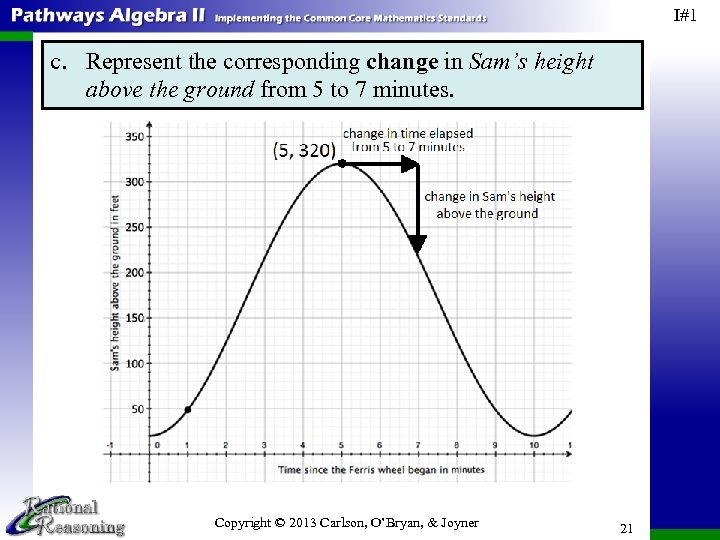 I#1 c. Represent the corresponding change in Sam’s height above the ground from 5 to 7 minutes. Copyright © 2013 Carlson, O’Bryan, & Joyner 21
I#1 c. Represent the corresponding change in Sam’s height above the ground from 5 to 7 minutes. Copyright © 2013 Carlson, O’Bryan, & Joyner 21
 I#1 d. Approximately what was the change in Sam’s height above ground over this time interval? Explain how you determined the value. Sam’s height above the ground changes by about – 105 feet. Estimates may vary slightly. e. Estimate Sam’s height above the ground 7 minutes since the Ferris wheel began moving and plot the point representing this information. We can use the graph or the information from part (d) to determine the new height. Sam is about 215 feet above the ground 7 minutes since the Ferris when began moving. Estimates may vary slightly. Copyright © 2013 Carlson, O’Bryan, & Joyner 22
I#1 d. Approximately what was the change in Sam’s height above ground over this time interval? Explain how you determined the value. Sam’s height above the ground changes by about – 105 feet. Estimates may vary slightly. e. Estimate Sam’s height above the ground 7 minutes since the Ferris wheel began moving and plot the point representing this information. We can use the graph or the information from part (d) to determine the new height. Sam is about 215 feet above the ground 7 minutes since the Ferris when began moving. Estimates may vary slightly. Copyright © 2013 Carlson, O’Bryan, & Joyner 22
 I#1 Additional videos are linked on the Rational Reasoning website and are located in the Pathways Dropbox. You can use these videos for additional practice with the ideas in this investigation. Copyright © 2013 Carlson, O’Bryan, & Joyner 23
I#1 Additional videos are linked on the Rational Reasoning website and are located in the Pathways Dropbox. You can use these videos for additional practice with the ideas in this investigation. Copyright © 2013 Carlson, O’Bryan, & Joyner 23
 Investigation #2
Investigation #2
 I#2 CHANGES IN QUANTITIES’ VALUES 1. In high school Maria grew from 62 inches tall to 74 inches tall. What was Maria’s change in height during high school? Her change in height was 12 inches because her height started at 62 inches and changed to 74 inches. We calculate the change with the expression 74 – 62. We can think of the answer as the number that makes the following statement true. 62 inches + (what change in height? ) = 74 inches Copyright © 2013 Carlson, O’Bryan, & Joyner 25
I#2 CHANGES IN QUANTITIES’ VALUES 1. In high school Maria grew from 62 inches tall to 74 inches tall. What was Maria’s change in height during high school? Her change in height was 12 inches because her height started at 62 inches and changed to 74 inches. We calculate the change with the expression 74 – 62. We can think of the answer as the number that makes the following statement true. 62 inches + (what change in height? ) = 74 inches Copyright © 2013 Carlson, O’Bryan, & Joyner 25
 I#2 2. Matt started a new diet, and over the last few months his weight went from 196. 7 pounds to 181. 2 pounds. What was the change in Matt’s weight? His change in weight was – 15. 5 pounds because his weight started at 196. 7 pounds and changed to 181. 2 pounds. We calculate the change with the expression 181. 2 – 196. 7. We can think of the answer as the number that makes the following statement true. 196. 7 pounds + (what change in weight? ) = 181. 2 pounds Copyright © 2013 Carlson, O’Bryan, & Joyner 26
I#2 2. Matt started a new diet, and over the last few months his weight went from 196. 7 pounds to 181. 2 pounds. What was the change in Matt’s weight? His change in weight was – 15. 5 pounds because his weight started at 196. 7 pounds and changed to 181. 2 pounds. We calculate the change with the expression 181. 2 – 196. 7. We can think of the answer as the number that makes the following statement true. 196. 7 pounds + (what change in weight? ) = 181. 2 pounds Copyright © 2013 Carlson, O’Bryan, & Joyner 26
 I#2 3. When Cyndi woke up this morning (6: 00 am) the temperature outside was – 6 o. F. When she got home from school (4: 00 pm) the temperature outside was 28 o. F. What was the change in temperature from 6: 00 am to 4: 00 pm? The change in temperature was 34 o. F because the temperature started at – 6 o. F and changed to 28 o. F. We calculate the change with the expression 28 – (– 6) or 28 + 6. We can think of the answer as the number that makes the following statement true. – 6 o. F + (what change in temperature? ) = 28 o. F Copyright © 2013 Carlson, O’Bryan, & Joyner 27
I#2 3. When Cyndi woke up this morning (6: 00 am) the temperature outside was – 6 o. F. When she got home from school (4: 00 pm) the temperature outside was 28 o. F. What was the change in temperature from 6: 00 am to 4: 00 pm? The change in temperature was 34 o. F because the temperature started at – 6 o. F and changed to 28 o. F. We calculate the change with the expression 28 – (– 6) or 28 + 6. We can think of the answer as the number that makes the following statement true. – 6 o. F + (what change in temperature? ) = 28 o. F Copyright © 2013 Carlson, O’Bryan, & Joyner 27
 I#2 Variable A variable is a letter used to represent the possible varying values of a quantity’s measure. Example: A bathtub, with a maximum volume of 42 gallons, starts off full and then drains to empty. Let v be the volume of water remaining in the bathtub (in gallons). Then v can represent any possible number from 0 to 42 as the water drains, such as v = 38 or v = 5. 7. Copyright © 2013 Carlson, O’Bryan, & Joyner 28
I#2 Variable A variable is a letter used to represent the possible varying values of a quantity’s measure. Example: A bathtub, with a maximum volume of 42 gallons, starts off full and then drains to empty. Let v be the volume of water remaining in the bathtub (in gallons). Then v can represent any possible number from 0 to 42 as the water drains, such as v = 38 or v = 5. 7. Copyright © 2013 Carlson, O’Bryan, & Joyner 28
 I#2 4 a. Define variables to represent the quantities’ values in Exercises #1 -3. (Answers may vary. ) Let h represent Maria’s height (in inches). Let w represent Matt’s weight (in pounds). Let t represent the outside temperature (in degrees Fahrenheit). Notice that in our variable definitions we describe the object and the attribute we are measuring as well as what units we are using to measure the attribute. Copyright © 2013 Carlson, O’Bryan, & Joyner 29
I#2 4 a. Define variables to represent the quantities’ values in Exercises #1 -3. (Answers may vary. ) Let h represent Maria’s height (in inches). Let w represent Matt’s weight (in pounds). Let t represent the outside temperature (in degrees Fahrenheit). Notice that in our variable definitions we describe the object and the attribute we are measuring as well as what units we are using to measure the attribute. Copyright © 2013 Carlson, O’Bryan, & Joyner 29
 I#2 b. What values might each variable take on? (Answers may vary. ) h might take on any value between about t = 20 and maybe t = 75 or t = 80 (depending on how tall Maria is when she stops growing). w might take on any value between about w = 10 and maybe w = 200 (depending on Matt’s highest weight). t might take on any value between about t = – 20 and maybe t = 100 (depending on where Cyndi lives). Note that we might choose a tighter set of values if we restrict ourselves to the time periods described in each context. Copyright © 2013 Carlson, O’Bryan, & Joyner 30
I#2 b. What values might each variable take on? (Answers may vary. ) h might take on any value between about t = 20 and maybe t = 75 or t = 80 (depending on how tall Maria is when she stops growing). w might take on any value between about w = 10 and maybe w = 200 (depending on Matt’s highest weight). t might take on any value between about t = – 20 and maybe t = 100 (depending on where Cyndi lives). Note that we might choose a tighter set of values if we restrict ourselves to the time periods described in each context. Copyright © 2013 Carlson, O’Bryan, & Joyner 30
 I#2 5. In January 2012, Caitlyn began saving money to make a down payment on a house. Let m be the number of months she’s been saving and let v represent the amount of money she’s saved (in dollars). a. What is the change in v from v = 940 to v = 2, 360? What does this represent? The change in v is 1420. Caitlyn saved up an additional $1420 towards her down payment. b. The change in v described in part (a) occurred as m changed from m = 3 to m = 7? What is the change in m and what does it represent? The change in m is 4. It took her four months to save the $1420 described in part (a). Copyright © 2013 Carlson, O’Bryan, & Joyner 31
I#2 5. In January 2012, Caitlyn began saving money to make a down payment on a house. Let m be the number of months she’s been saving and let v represent the amount of money she’s saved (in dollars). a. What is the change in v from v = 940 to v = 2, 360? What does this represent? The change in v is 1420. Caitlyn saved up an additional $1420 towards her down payment. b. The change in v described in part (a) occurred as m changed from m = 3 to m = 7? What is the change in m and what does it represent? The change in m is 4. It took her four months to save the $1420 described in part (a). Copyright © 2013 Carlson, O’Bryan, & Joyner 31
 I#2 6. Let x, y, and z represent the values of three different quantities. a. If the value of x goes from x = 1 to x = 10, what is the change in x? The change in x is 9 (represented by the expression 10 – 1). b. If the value of x changes to x = – 5 from x = 3, what is the change in x? The change in x is – 8 (represented by the expression – 5 – 3). c. If the value of z changes to z = 18. 07 from z = 3. 15, what is the change in z? The change in z is 14. 92 (represented by the expression 18. 07 – 3. 15). d. If the value of y goes from y = 6 to y = p, what is the change in y? The change in y is p – 6. Copyright © 2013 Carlson, O’Bryan, & Joyner 32
I#2 6. Let x, y, and z represent the values of three different quantities. a. If the value of x goes from x = 1 to x = 10, what is the change in x? The change in x is 9 (represented by the expression 10 – 1). b. If the value of x changes to x = – 5 from x = 3, what is the change in x? The change in x is – 8 (represented by the expression – 5 – 3). c. If the value of z changes to z = 18. 07 from z = 3. 15, what is the change in z? The change in z is 14. 92 (represented by the expression 18. 07 – 3. 15). d. If the value of y goes from y = 6 to y = p, what is the change in y? The change in y is p – 6. Copyright © 2013 Carlson, O’Bryan, & Joyner 32
 I#2 Changes in Quantities’ Values Suppose x is the value of Quantity A and y is the value of Quantity B. Then ∆x represents a change in the value of Quantity A and ∆y represents a change in the value of Quantity B. Example 1: If we let x change from x = 4 to x = 11, then ∆x = 7 which we calculate with the expression 11 – 4. Example 2: If we let y change from y = 8 to y = 5, then ∆y = – 3 which we calculate with the expression 5 – 8. Copyright © 2013 Carlson, O’Bryan, & Joyner 33
I#2 Changes in Quantities’ Values Suppose x is the value of Quantity A and y is the value of Quantity B. Then ∆x represents a change in the value of Quantity A and ∆y represents a change in the value of Quantity B. Example 1: If we let x change from x = 4 to x = 11, then ∆x = 7 which we calculate with the expression 11 – 4. Example 2: If we let y change from y = 8 to y = 5, then ∆y = – 3 which we calculate with the expression 5 – 8. Copyright © 2013 Carlson, O’Bryan, & Joyner 33
 I#2 7. Suppose Gerald bought a tree and planted it in his yard last summer. At the time of planting it was 4. 5 feet tall. Let h represent the height of the tree in feet. a. What is the difference between saying h = 5 and ∆h = 5? Saying h = 5 is stating that the height of the tree is 5 feet. Saying ∆h = 5 is stating that the change in height was 5 feet (so the tree grew 5 feet over some time period). Copyright © 2013 Carlson, O’Bryan, & Joyner 34
I#2 7. Suppose Gerald bought a tree and planted it in his yard last summer. At the time of planting it was 4. 5 feet tall. Let h represent the height of the tree in feet. a. What is the difference between saying h = 5 and ∆h = 5? Saying h = 5 is stating that the height of the tree is 5 feet. Saying ∆h = 5 is stating that the change in height was 5 feet (so the tree grew 5 feet over some time period). Copyright © 2013 Carlson, O’Bryan, & Joyner 34
 I#2 7. Suppose Gerald bought a tree and planted it in his yard last summer. At the time of planting it was 4. 5 feet tall. Let h represent the height of the tree in feet. b. If we substitute h = 6. 8 into the expression h – 4. 5, what are we calculating? We are calculating the change in the tree’s height (∆h) from when it was 4. 5 feet tall to when it was 6. 8 feet tall. c. If we substitute h = 10. 7 into the expression h – 6. 8, what are we calculating? We are calculating the change in the tree’s height (∆h) from when it was 6. 8 feet tall to when it was 10. 7 feet tall. Copyright © 2013 Carlson, O’Bryan, & Joyner 35
I#2 7. Suppose Gerald bought a tree and planted it in his yard last summer. At the time of planting it was 4. 5 feet tall. Let h represent the height of the tree in feet. b. If we substitute h = 6. 8 into the expression h – 4. 5, what are we calculating? We are calculating the change in the tree’s height (∆h) from when it was 4. 5 feet tall to when it was 6. 8 feet tall. c. If we substitute h = 10. 7 into the expression h – 6. 8, what are we calculating? We are calculating the change in the tree’s height (∆h) from when it was 6. 8 feet tall to when it was 10. 7 feet tall. Copyright © 2013 Carlson, O’Bryan, & Joyner 35
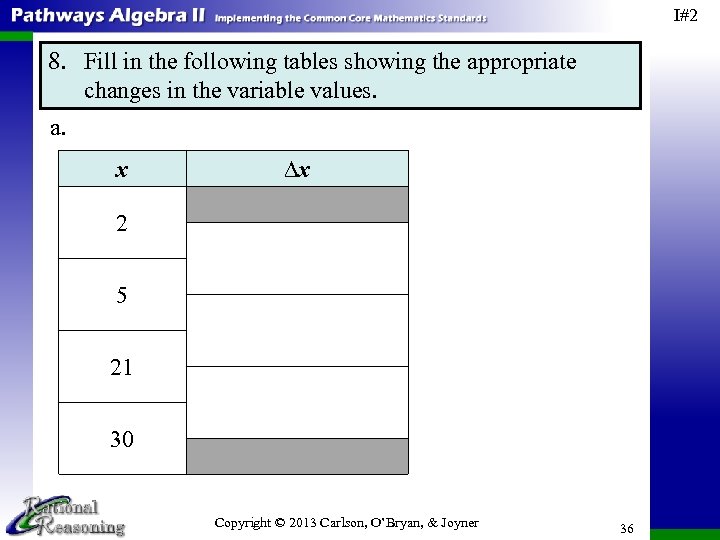 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 5 21 30 Copyright © 2013 Carlson, O’Bryan, & Joyner 36
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 5 21 30 Copyright © 2013 Carlson, O’Bryan, & Joyner 36
 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 5 – 2 5 The change in x from x = 2 to x = 5 is 3. 21 30 Copyright © 2013 Carlson, O’Bryan, & Joyner 37
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 5 – 2 5 The change in x from x = 2 to x = 5 is 3. 21 30 Copyright © 2013 Carlson, O’Bryan, & Joyner 37
 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 3 5 The change in x from x = 2 to x = 5 is 3. 21 30 Copyright © 2013 Carlson, O’Bryan, & Joyner 38
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 3 5 The change in x from x = 2 to x = 5 is 3. 21 30 Copyright © 2013 Carlson, O’Bryan, & Joyner 38
 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 3 5 21 – 5 21 The change in x from x = 5 to x = 21 is 16. 30 Copyright © 2013 Carlson, O’Bryan, & Joyner 39
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 3 5 21 – 5 21 The change in x from x = 5 to x = 21 is 16. 30 Copyright © 2013 Carlson, O’Bryan, & Joyner 39
 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 3 5 16 21 The change in x from x = 5 to x = 21 is 16. 30 Copyright © 2013 Carlson, O’Bryan, & Joyner 40
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 3 5 16 21 The change in x from x = 5 to x = 21 is 16. 30 Copyright © 2013 Carlson, O’Bryan, & Joyner 40
 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 3 5 16 21 30 – 21 30 The change in x from x = 21 to x = 30 is 9. Copyright © 2013 Carlson, O’Bryan, & Joyner 41
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 3 5 16 21 30 – 21 30 The change in x from x = 21 to x = 30 is 9. Copyright © 2013 Carlson, O’Bryan, & Joyner 41
 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 3 5 16 21 9 30 The change in x from x = 21 to x = 30 is 9. Copyright © 2013 Carlson, O’Bryan, & Joyner 42
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. a. x ∆x 2 3 5 16 21 9 30 The change in x from x = 21 to x = 30 is 9. Copyright © 2013 Carlson, O’Bryan, & Joyner 42
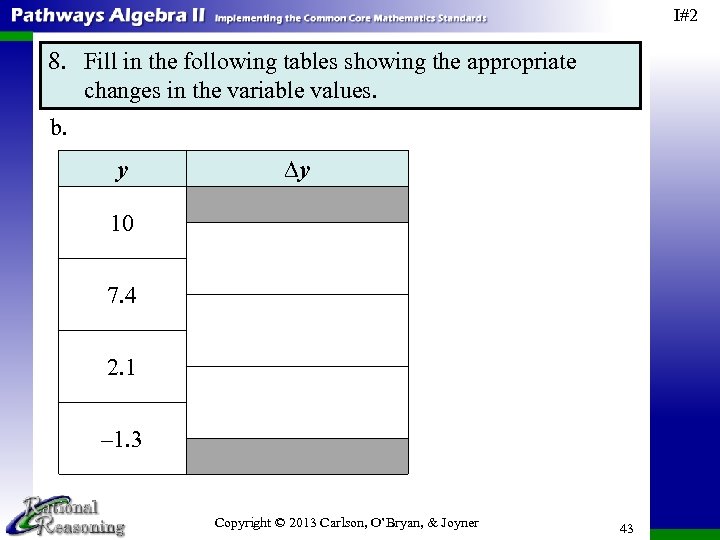 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. b. y ∆y 10 7. 4 2. 1 – 1. 3 Copyright © 2013 Carlson, O’Bryan, & Joyner 43
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. b. y ∆y 10 7. 4 2. 1 – 1. 3 Copyright © 2013 Carlson, O’Bryan, & Joyner 43
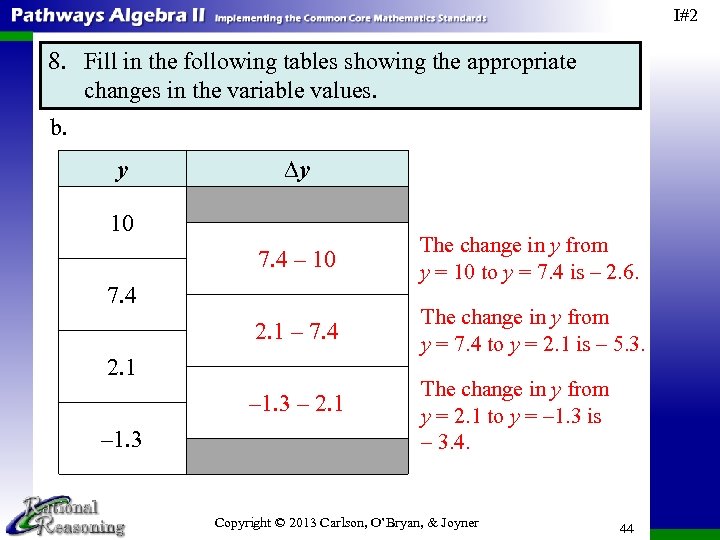 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. b. y ∆y 10 7. 4 – 10 The change in y from y = 10 to y = 7. 4 is – 2. 6. 2. 1 – 7. 4 The change in y from y = 7. 4 to y = 2. 1 is – 5. 3. 7. 4 2. 1 – 1. 3 – 2. 1 – 1. 3 The change in y from y = 2. 1 to y = – 1. 3 is – 3. 4. Copyright © 2013 Carlson, O’Bryan, & Joyner 44
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. b. y ∆y 10 7. 4 – 10 The change in y from y = 10 to y = 7. 4 is – 2. 6. 2. 1 – 7. 4 The change in y from y = 7. 4 to y = 2. 1 is – 5. 3. 7. 4 2. 1 – 1. 3 – 2. 1 – 1. 3 The change in y from y = 2. 1 to y = – 1. 3 is – 3. 4. Copyright © 2013 Carlson, O’Bryan, & Joyner 44
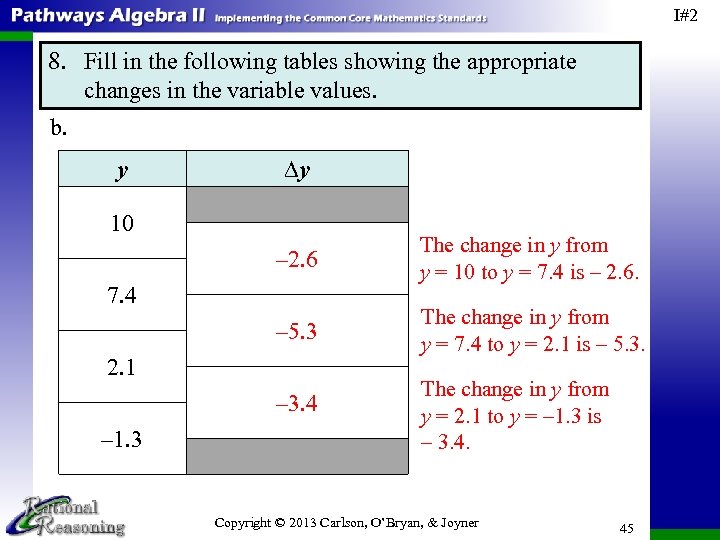 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. b. y ∆y 10 – 2. 6 The change in y from y = 10 to y = 7. 4 is – 2. 6. – 5. 3 The change in y from y = 7. 4 to y = 2. 1 is – 5. 3. 7. 4 2. 1 – 3. 4 – 1. 3 The change in y from y = 2. 1 to y = – 1. 3 is – 3. 4. Copyright © 2013 Carlson, O’Bryan, & Joyner 45
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. b. y ∆y 10 – 2. 6 The change in y from y = 10 to y = 7. 4 is – 2. 6. – 5. 3 The change in y from y = 7. 4 to y = 2. 1 is – 5. 3. 7. 4 2. 1 – 3. 4 – 1. 3 The change in y from y = 2. 1 to y = – 1. 3 is – 3. 4. Copyright © 2013 Carlson, O’Bryan, & Joyner 45
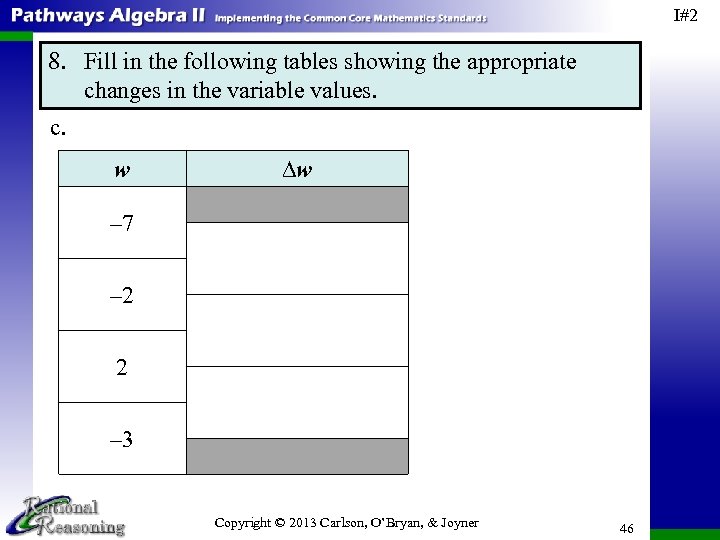 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. c. w ∆w – 7 – 2 2 – 3 Copyright © 2013 Carlson, O’Bryan, & Joyner 46
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. c. w ∆w – 7 – 2 2 – 3 Copyright © 2013 Carlson, O’Bryan, & Joyner 46
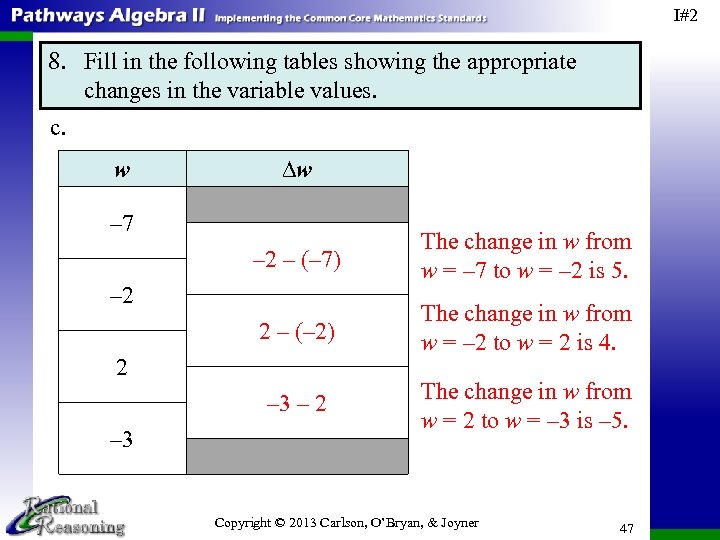 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. c. w ∆w – 7 – 2 – (– 7) The change in w from w = – 7 to w = – 2 is 5. 2 – (– 2) The change in w from w = – 2 to w = 2 is 4. – 3 – 2 The change in w from w = 2 to w = – 3 is – 5. – 2 2 – 3 Copyright © 2013 Carlson, O’Bryan, & Joyner 47
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. c. w ∆w – 7 – 2 – (– 7) The change in w from w = – 7 to w = – 2 is 5. 2 – (– 2) The change in w from w = – 2 to w = 2 is 4. – 3 – 2 The change in w from w = 2 to w = – 3 is – 5. – 2 2 – 3 Copyright © 2013 Carlson, O’Bryan, & Joyner 47
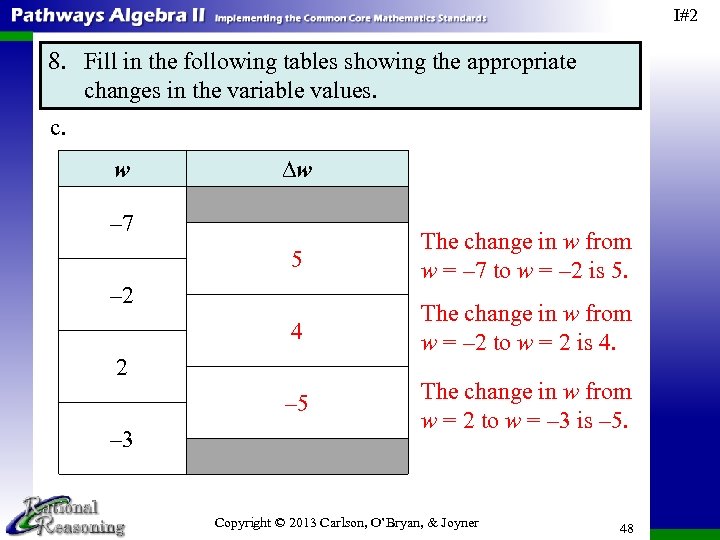 I#2 8. Fill in the following tables showing the appropriate changes in the variable values. c. w ∆w – 7 5 The change in w from w = – 7 to w = – 2 is 5. 4 The change in w from w = – 2 to w = 2 is 4. – 5 The change in w from w = 2 to w = – 3 is – 5. – 2 2 – 3 Copyright © 2013 Carlson, O’Bryan, & Joyner 48
I#2 8. Fill in the following tables showing the appropriate changes in the variable values. c. w ∆w – 7 5 The change in w from w = – 7 to w = – 2 is 5. 4 The change in w from w = – 2 to w = 2 is 4. – 5 The change in w from w = 2 to w = – 3 is – 5. – 2 2 – 3 Copyright © 2013 Carlson, O’Bryan, & Joyner 48
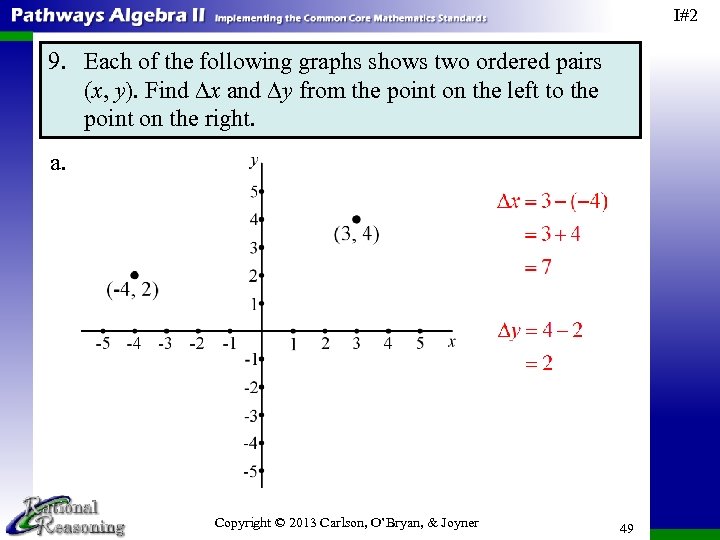 I#2 9. Each of the following graphs shows two ordered pairs (x, y). Find ∆x and ∆y from the point on the left to the point on the right. a. Copyright © 2013 Carlson, O’Bryan, & Joyner 49
I#2 9. Each of the following graphs shows two ordered pairs (x, y). Find ∆x and ∆y from the point on the left to the point on the right. a. Copyright © 2013 Carlson, O’Bryan, & Joyner 49
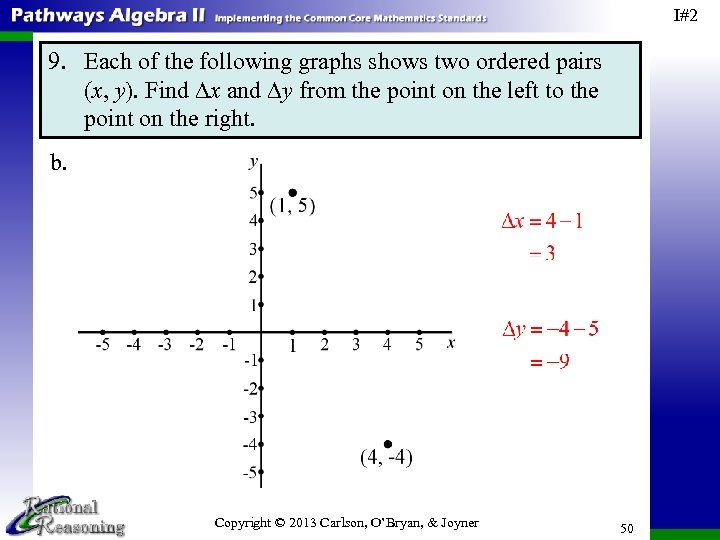 I#2 9. Each of the following graphs shows two ordered pairs (x, y). Find ∆x and ∆y from the point on the left to the point on the right. b. Copyright © 2013 Carlson, O’Bryan, & Joyner 50
I#2 9. Each of the following graphs shows two ordered pairs (x, y). Find ∆x and ∆y from the point on the left to the point on the right. b. Copyright © 2013 Carlson, O’Bryan, & Joyner 50
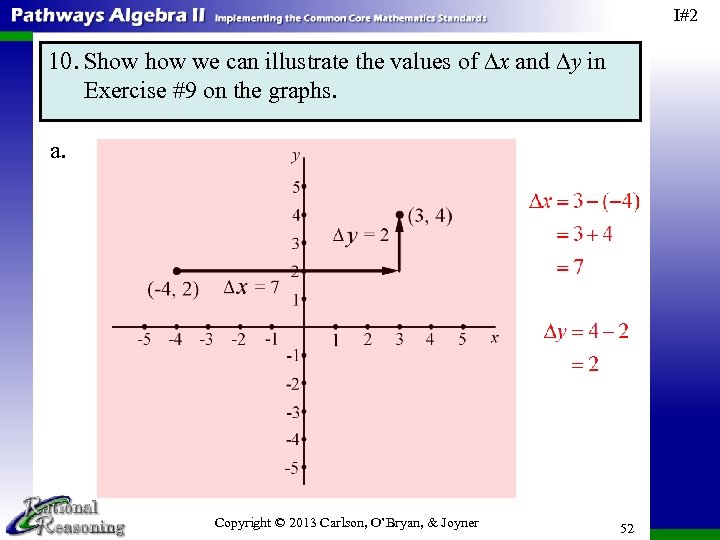
 I#2 10. Show we can illustrate the values of ∆x and ∆y in Exercise #9 on the graphs. a. Copyright © 2013 Carlson, O’Bryan, & Joyner 51
I#2 10. Show we can illustrate the values of ∆x and ∆y in Exercise #9 on the graphs. a. Copyright © 2013 Carlson, O’Bryan, & Joyner 51
 I#2 10. Show we can illustrate the values of ∆x and ∆y in Exercise #9 on the graphs. a. Copyright © 2013 Carlson, O’Bryan, & Joyner 52
I#2 10. Show we can illustrate the values of ∆x and ∆y in Exercise #9 on the graphs. a. Copyright © 2013 Carlson, O’Bryan, & Joyner 52
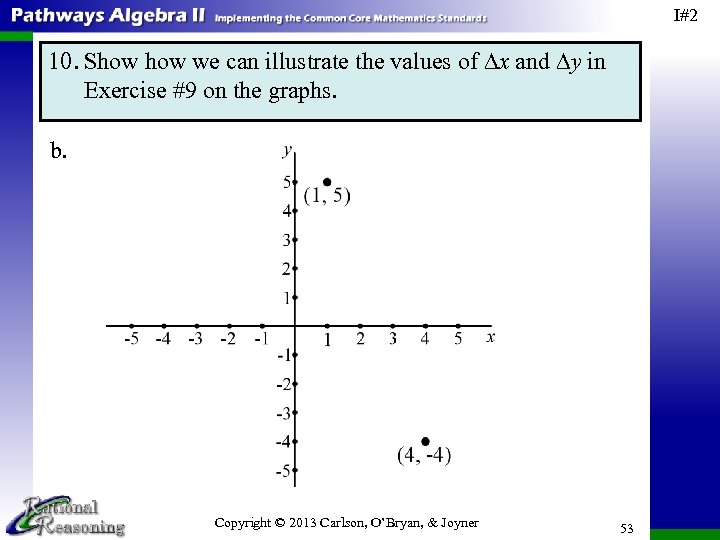 I#2 10. Show we can illustrate the values of ∆x and ∆y in Exercise #9 on the graphs. b. Copyright © 2013 Carlson, O’Bryan, & Joyner 53
I#2 10. Show we can illustrate the values of ∆x and ∆y in Exercise #9 on the graphs. b. Copyright © 2013 Carlson, O’Bryan, & Joyner 53
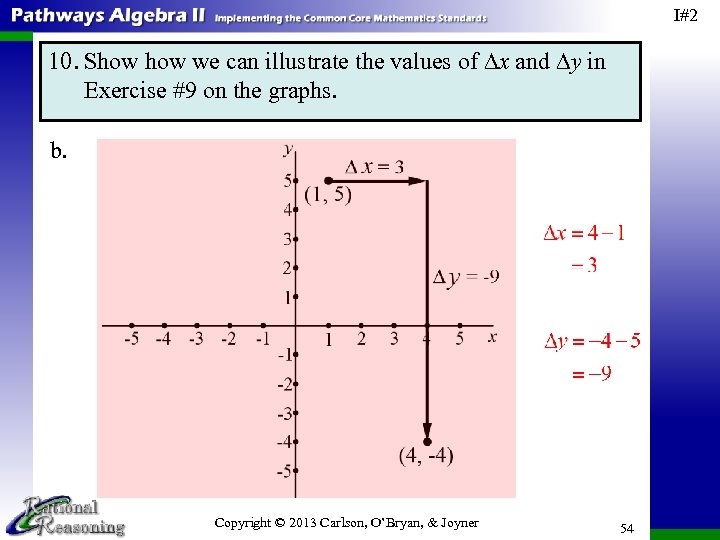 I#2 10. Show we can illustrate the values of ∆x and ∆y in Exercise #9 on the graphs. b. Copyright © 2013 Carlson, O’Bryan, & Joyner 54
I#2 10. Show we can illustrate the values of ∆x and ∆y in Exercise #9 on the graphs. b. Copyright © 2013 Carlson, O’Bryan, & Joyner 54
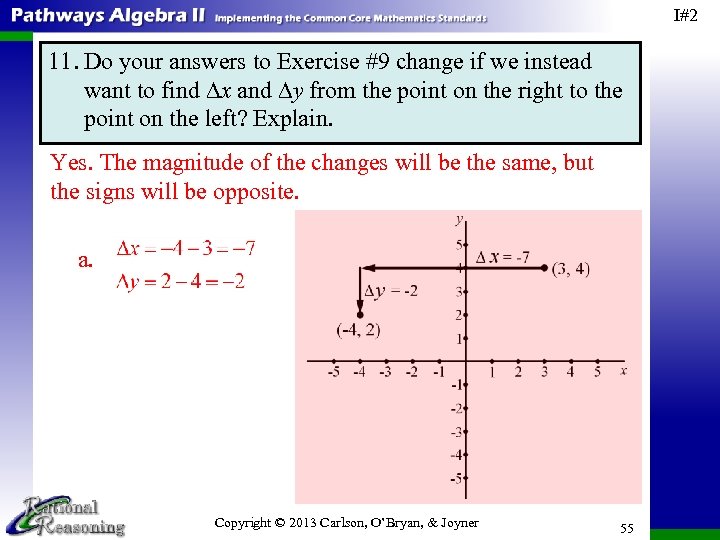 I#2 11. Do your answers to Exercise #9 change if we instead want to find ∆x and ∆y from the point on the right to the point on the left? Explain. Yes. The magnitude of the changes will be the same, but the signs will be opposite. a. Copyright © 2013 Carlson, O’Bryan, & Joyner 55
I#2 11. Do your answers to Exercise #9 change if we instead want to find ∆x and ∆y from the point on the right to the point on the left? Explain. Yes. The magnitude of the changes will be the same, but the signs will be opposite. a. Copyright © 2013 Carlson, O’Bryan, & Joyner 55
 I#2 11. Do your answers to Exercise #9 change if we instead want to find ∆x and ∆y from the point on the right to the point on the left? Explain. Yes. The magnitude of the changes will be the same, but the signs will be opposite. b. Copyright © 2013 Carlson, O’Bryan, & Joyner 56
I#2 11. Do your answers to Exercise #9 change if we instead want to find ∆x and ∆y from the point on the right to the point on the left? Explain. Yes. The magnitude of the changes will be the same, but the signs will be opposite. b. Copyright © 2013 Carlson, O’Bryan, & Joyner 56
 I#2 12. Suppose we start with a value of x = – 3. a. What expression represents the change in x from x = – 3 to any possible value of x? b. Repeat part (a) if our initial reference value is x = – 7 instead of x = – 3. c. Repeat part (a) if our initial reference value is x = 1. 2 instead of x = – 3. Copyright © 2013 Carlson, O’Bryan, & Joyner 57
I#2 12. Suppose we start with a value of x = – 3. a. What expression represents the change in x from x = – 3 to any possible value of x? b. Repeat part (a) if our initial reference value is x = – 7 instead of x = – 3. c. Repeat part (a) if our initial reference value is x = 1. 2 instead of x = – 3. Copyright © 2013 Carlson, O’Bryan, & Joyner 57
 I#2 13. Think about the idea of the change in a variable from one value to another. What do the following expressions represent when we substitute a value for the variable? a. x – 34 The change in x from x = 34 to whatever value of x we substitute. For example, if we substitute x = 30, then 30 – 34 = – 4, telling us that the change in x from x = 34 to x = 30 is – 4. Copyright © 2013 Carlson, O’Bryan, & Joyner 58
I#2 13. Think about the idea of the change in a variable from one value to another. What do the following expressions represent when we substitute a value for the variable? a. x – 34 The change in x from x = 34 to whatever value of x we substitute. For example, if we substitute x = 30, then 30 – 34 = – 4, telling us that the change in x from x = 34 to x = 30 is – 4. Copyright © 2013 Carlson, O’Bryan, & Joyner 58
 I#2 13. Think about the idea of the change in a variable from one value to another. What do the following expressions represent when we substitute a value for the variable? b. y – (– 2) [or y + 2] The change in y from y = – 2 to whatever value of y we substitute. For example, if we substitute y = 5, then 5 + 2 = 7, telling us that the change in y from y = – 2 to y = 5 is 7. Copyright © 2013 Carlson, O’Bryan, & Joyner 59
I#2 13. Think about the idea of the change in a variable from one value to another. What do the following expressions represent when we substitute a value for the variable? b. y – (– 2) [or y + 2] The change in y from y = – 2 to whatever value of y we substitute. For example, if we substitute y = 5, then 5 + 2 = 7, telling us that the change in y from y = – 2 to y = 5 is 7. Copyright © 2013 Carlson, O’Bryan, & Joyner 59
 I#2 13. Think about the idea of the change in a variable from one value to another. What do the following expressions represent when we substitute a value for the variable? c. r – 4. 7 The change in r from r = 4. 7 to whatever value of r we substitute. For example, if we substitute r = 5, then 5 – 4. 7 = 0. 3, telling us that the change in r from r = 4. 7 to r = 5 is 0. 3. Copyright © 2013 Carlson, O’Bryan, & Joyner 60
I#2 13. Think about the idea of the change in a variable from one value to another. What do the following expressions represent when we substitute a value for the variable? c. r – 4. 7 The change in r from r = 4. 7 to whatever value of r we substitute. For example, if we substitute r = 5, then 5 – 4. 7 = 0. 3, telling us that the change in r from r = 4. 7 to r = 5 is 0. 3. Copyright © 2013 Carlson, O’Bryan, & Joyner 60
 I#2 13. Think about the idea of the change in a variable from one value to another. What do the following expressions represent when we substitute a value for the variable? d. p – (– 13. 8) [or p + 13. 8] The change in p from p = – 13. 8 to whatever value of p we substitute. For example, if we substitute p = – 8, then – 8 + 13. 8 = 5. 8, telling us that the change in p from p = – 13. 8 to p = – 8 is 5. 8. Copyright © 2013 Carlson, O’Bryan, & Joyner 61
I#2 13. Think about the idea of the change in a variable from one value to another. What do the following expressions represent when we substitute a value for the variable? d. p – (– 13. 8) [or p + 13. 8] The change in p from p = – 13. 8 to whatever value of p we substitute. For example, if we substitute p = – 8, then – 8 + 13. 8 = 5. 8, telling us that the change in p from p = – 13. 8 to p = – 8 is 5. 8. Copyright © 2013 Carlson, O’Bryan, & Joyner 61
 Investigation #3
Investigation #3
 I#3 CONSTANT RATE OF CHANGE You’ve probably heard someone use the phrase “constant speed” before. For example, you might hear “He was driving at a constant speed of 45 miles per hour. ” In this investigation we will explore the idea of constant speed (and more generally constant rate of change) and link this back to your work with changes in quantities from Investigation 2. For Exercises #1 -6 use the “Jane Walking” applet. Jane is walking from her home to work. When she passes her mailbox she is 25 feet from her house. Between the mailbox and a tree she walks at a constant speed, covering 40 feet in 8 seconds. Jane Walking Applet Copyright © 2013 Carlson, O’Bryan, & Joyner 63
I#3 CONSTANT RATE OF CHANGE You’ve probably heard someone use the phrase “constant speed” before. For example, you might hear “He was driving at a constant speed of 45 miles per hour. ” In this investigation we will explore the idea of constant speed (and more generally constant rate of change) and link this back to your work with changes in quantities from Investigation 2. For Exercises #1 -6 use the “Jane Walking” applet. Jane is walking from her home to work. When she passes her mailbox she is 25 feet from her house. Between the mailbox and a tree she walks at a constant speed, covering 40 feet in 8 seconds. Jane Walking Applet Copyright © 2013 Carlson, O’Bryan, & Joyner 63
 I#3 1. After Jane passes the mailbox, how long does it take her to travel 20 feet? Explain your thinking. It takes her 4 seconds to travel 20 feet because 20 feet is times as far as 40 feet, so it will take her times as long as 8 seconds to cover this distance. 2. After Jane passes the mailbox, how far does she travel in 2 seconds? 6 seconds? Explain your thinking. (Student reasoning might vary. We give only one possible way of thinking. ) She travels 10 feet and 30 feet respectively. 2 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. 6 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. Copyright © 2013 Carlson, O’Bryan, & Joyner 64
I#3 1. After Jane passes the mailbox, how long does it take her to travel 20 feet? Explain your thinking. It takes her 4 seconds to travel 20 feet because 20 feet is times as far as 40 feet, so it will take her times as long as 8 seconds to cover this distance. 2. After Jane passes the mailbox, how far does she travel in 2 seconds? 6 seconds? Explain your thinking. (Student reasoning might vary. We give only one possible way of thinking. ) She travels 10 feet and 30 feet respectively. 2 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. 6 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. Copyright © 2013 Carlson, O’Bryan, & Joyner 64
 I#3 3. Let’s draw line segments to represent the total distance traveled from the mailbox to the tree and the amount of elapsed time it takes to cover this distance. Demonstrate how we can use these line segments to represent the reasoning in Exercises #1 -2. We can partition the line segments to see how these two quantities correspond. Copyright © 2013 Carlson, O’Bryan, & Joyner 65
I#3 3. Let’s draw line segments to represent the total distance traveled from the mailbox to the tree and the amount of elapsed time it takes to cover this distance. Demonstrate how we can use these line segments to represent the reasoning in Exercises #1 -2. We can partition the line segments to see how these two quantities correspond. Copyright © 2013 Carlson, O’Bryan, & Joyner 65
 I#3 3. Let’s draw line segments to represent the total distance traveled from the mailbox to the tree and the amount of elapsed time it takes to cover this distance. It takes her 4 seconds to travel 20 feet because 20 feet is times as far as 40 feet, so it will take her times as long as 8 seconds to cover this distance. Copyright © 2013 Carlson, O’Bryan, & Joyner 66
I#3 3. Let’s draw line segments to represent the total distance traveled from the mailbox to the tree and the amount of elapsed time it takes to cover this distance. It takes her 4 seconds to travel 20 feet because 20 feet is times as far as 40 feet, so it will take her times as long as 8 seconds to cover this distance. Copyright © 2013 Carlson, O’Bryan, & Joyner 66
 I#3 3. Let’s draw line segments to represent the total distance traveled from the mailbox to the tree and the amount of elapsed time it takes to cover this distance. She travels 10 feet and 30 feet respectively. 2 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. 6 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. Copyright © 2013 Carlson, O’Bryan, & Joyner 67
I#3 3. Let’s draw line segments to represent the total distance traveled from the mailbox to the tree and the amount of elapsed time it takes to cover this distance. She travels 10 feet and 30 feet respectively. 2 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. 6 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. Copyright © 2013 Carlson, O’Bryan, & Joyner 67
 I#3 3. Let’s draw line segments to represent the total distance traveled from the mailbox to the tree and the amount of elapsed time it takes to cover this distance. She travels 10 feet and 30 feet respectively. 2 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. 6 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. Copyright © 2013 Carlson, O’Bryan, & Joyner 68
I#3 3. Let’s draw line segments to represent the total distance traveled from the mailbox to the tree and the amount of elapsed time it takes to cover this distance. She travels 10 feet and 30 feet respectively. 2 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. 6 seconds is times as long as 8 seconds, so she will travel times as far as 40 feet. Copyright © 2013 Carlson, O’Bryan, & Joyner 68
 I#3 4. Use the line segments in Exercise #3 and the applet to help you answer the following questions. a. How far will she travel during any 1 -second time interval between the mailbox and the tree? 5 feet during any 1 -second interval Copyright © 2013 Carlson, O’Bryan, & Joyner 69
I#3 4. Use the line segments in Exercise #3 and the applet to help you answer the following questions. a. How far will she travel during any 1 -second time interval between the mailbox and the tree? 5 feet during any 1 -second interval Copyright © 2013 Carlson, O’Bryan, & Joyner 69
 I#3 4. Use the line segments in Exercise #3 and the applet to help you answer the following questions. b. How long will it take her to travel any 1 -foot distance between the mailbox and tree? 0. 2 seconds to cover any 1 -foot distance between mailbox and tree Copyright © 2013 Carlson, O’Bryan, & Joyner 70
I#3 4. Use the line segments in Exercise #3 and the applet to help you answer the following questions. b. How long will it take her to travel any 1 -foot distance between the mailbox and tree? 0. 2 seconds to cover any 1 -foot distance between mailbox and tree Copyright © 2013 Carlson, O’Bryan, & Joyner 70
 I#3 5. How do your answers to Exercise #4 help you find a. how far Jane travels for any change in the time elapsed since she passed the mailbox? (For example, how far does Jane travel for a change in time elapsed of 2. 8 seconds? ) Once we know the unit rate, this allows us to scale to any multiple we want. We know that in 1 second she travels 5 feet, so in 2. 8 seconds (2. 8 times as long as 1 second) she travels 2. 8 times as far as 5 feet, or 2. 8(5) = 14 feet. Copyright © 2013 Carlson, O’Bryan, & Joyner 71
I#3 5. How do your answers to Exercise #4 help you find a. how far Jane travels for any change in the time elapsed since she passed the mailbox? (For example, how far does Jane travel for a change in time elapsed of 2. 8 seconds? ) Once we know the unit rate, this allows us to scale to any multiple we want. We know that in 1 second she travels 5 feet, so in 2. 8 seconds (2. 8 times as long as 1 second) she travels 2. 8 times as far as 5 feet, or 2. 8(5) = 14 feet. Copyright © 2013 Carlson, O’Bryan, & Joyner 71
 I#3 5. How do your answers to Exercise #4 help you find b. how long it takes Jane to travel any distance between the mailbox and tree? (For example, how long does it take Jane to travel 33 feet? ) Once we know the unit rate, this allows us to scale to any multiple we want. We know it takes her 0. 2 seconds to travel 1 foot, so to travel 33 feet (33 times as far as 1 foot) it will take her 33 times as long as 0. 2 seconds, or 33(0. 2) = 6. 6 seconds. Copyright © 2013 Carlson, O’Bryan, & Joyner 72
I#3 5. How do your answers to Exercise #4 help you find b. how long it takes Jane to travel any distance between the mailbox and tree? (For example, how long does it take Jane to travel 33 feet? ) Once we know the unit rate, this allows us to scale to any multiple we want. We know it takes her 0. 2 seconds to travel 1 foot, so to travel 33 feet (33 times as far as 1 foot) it will take her 33 times as long as 0. 2 seconds, or 33(0. 2) = 6. 6 seconds. Copyright © 2013 Carlson, O’Bryan, & Joyner 72
 I#3 6. Think about the work you did with the “Jane Walking” applet. What does it mean for an object to move at a constant speed? (Note: Please say something more than “The speed doesn’t change” – be descriptive and reference specific quantities. ) Explanations will vary. Some important observations could include the following. For an object traveling at a constant speed, the same change in time elapsed will always correspond to equal changes in distance traveled, and likewise the same change in distance traveled will correspond to equal changes in time elapsed. Furthermore, if we know how far the object travels in some total amount of time, then in some fraction of the total time it will travel the same fraction of the total distance. Copyright © 2013 Carlson, O’Bryan, & Joyner 73
I#3 6. Think about the work you did with the “Jane Walking” applet. What does it mean for an object to move at a constant speed? (Note: Please say something more than “The speed doesn’t change” – be descriptive and reference specific quantities. ) Explanations will vary. Some important observations could include the following. For an object traveling at a constant speed, the same change in time elapsed will always correspond to equal changes in distance traveled, and likewise the same change in distance traveled will correspond to equal changes in time elapsed. Furthermore, if we know how far the object travels in some total amount of time, then in some fraction of the total time it will travel the same fraction of the total distance. Copyright © 2013 Carlson, O’Bryan, & Joyner 73
 I#3 7. Felipe was walking to school today. Assume that he walked at a constant speed during the entire trip, and also suppose that during one part of the trip he walked 70 feet in 16 seconds. a. Provide at least four conclusions we can draw from the given information. Answers will vary. Some examples are given. He walked 35 feet ( times as far as 70 feet) in times as long as 16 seconds (or 8 seconds). If the trip was long enough, he walked 280 feet (4 times as far as 70 feet) in 64 seconds (4 times as long as 16 seconds). Copyright © 2013 Carlson, O’Bryan, & Joyner 74
I#3 7. Felipe was walking to school today. Assume that he walked at a constant speed during the entire trip, and also suppose that during one part of the trip he walked 70 feet in 16 seconds. a. Provide at least four conclusions we can draw from the given information. Answers will vary. Some examples are given. He walked 35 feet ( times as far as 70 feet) in times as long as 16 seconds (or 8 seconds). If the trip was long enough, he walked 280 feet (4 times as far as 70 feet) in 64 seconds (4 times as long as 16 seconds). Copyright © 2013 Carlson, O’Bryan, & Joyner 74
 I#3 b. How far did Felipe travel in 3 seconds? Felipe travels 4. 375 feet over any 1 -second interval, so in 3 seconds he travels 3(4. 375) = 13. 125 feet. c. Does your answer to part (b) depend on which 3 -second interval we’re talking about? Explain. No. Over any 3 -minute interval during this part of his trip he travels 13. 125 feet because his speed was constant. d. How long did it take Felipe to travel any 10 -foot distance during this part of his trip? It takes him of a second to travel 1 foot, so to travel 10 feet it takes seconds. Copyright © 2013 Carlson, O’Bryan, & Joyner 75
I#3 b. How far did Felipe travel in 3 seconds? Felipe travels 4. 375 feet over any 1 -second interval, so in 3 seconds he travels 3(4. 375) = 13. 125 feet. c. Does your answer to part (b) depend on which 3 -second interval we’re talking about? Explain. No. Over any 3 -minute interval during this part of his trip he travels 13. 125 feet because his speed was constant. d. How long did it take Felipe to travel any 10 -foot distance during this part of his trip? It takes him of a second to travel 1 foot, so to travel 10 feet it takes seconds. Copyright © 2013 Carlson, O’Bryan, & Joyner 75
 I#3 8. Assume that a baseball and a tennis ball are both traveling at constant speeds (but not necessarily the same speed). a. What does it mean to say that the tennis ball is traveling faster than the baseball? Be descriptive, and reference the specific quantities involved. For any given amount of time elapsed, the tennis ball will cover a greater distance than the baseball will in the same amount of elapsed time. Similarly, for any given amount of distance, the tennis ball will cover that distance in less time than it takes the baseball to cover that distance. Copyright © 2013 Carlson, O’Bryan, & Joyner 76
I#3 8. Assume that a baseball and a tennis ball are both traveling at constant speeds (but not necessarily the same speed). a. What does it mean to say that the tennis ball is traveling faster than the baseball? Be descriptive, and reference the specific quantities involved. For any given amount of time elapsed, the tennis ball will cover a greater distance than the baseball will in the same amount of elapsed time. Similarly, for any given amount of distance, the tennis ball will cover that distance in less time than it takes the baseball to cover that distance. Copyright © 2013 Carlson, O’Bryan, & Joyner 76
 I#3 8. Assume that a baseball and a tennis ball are both traveling at constant speeds (but not necessarily the same speed). b. What does it mean if the baseball and tennis ball have the same constant speed? Be descriptive, and reference the specific quantities involved. For any given elapsed time, the two objects will cover the same amount of distance. Likewise, for any specific amount of distance, it will take the same amount of time for both objects to travel that distance. Copyright © 2013 Carlson, O’Bryan, & Joyner 77
I#3 8. Assume that a baseball and a tennis ball are both traveling at constant speeds (but not necessarily the same speed). b. What does it mean if the baseball and tennis ball have the same constant speed? Be descriptive, and reference the specific quantities involved. For any given elapsed time, the two objects will cover the same amount of distance. Likewise, for any specific amount of distance, it will take the same amount of time for both objects to travel that distance. Copyright © 2013 Carlson, O’Bryan, & Joyner 77
 I#3 9. Suppose we want to rank the following objects in order from fastest to slowest. Assume each object is traveling at a constant speed (but not necessarily the same constant speed). Bike: 11 feet in 0. 5 second Runner: 112 feet in 7 seconds Car: 212 feet in 10 seconds Football: 52. 5 feet in 3 seconds Bird: 4. 24 feet in 0. 2 second Water Balloon: 24 feet in 1. 5 seconds a. Why is it difficult to compare the objects’ speeds based on the information given? The distances traveled and the corresponding time intervals are all different – we can’t determine which objects travel further in a fixed amount of time or which objects cover the same amount of distance in less time by simply looking at the given information. Copyright © 2013 Carlson, O’Bryan, & Joyner 78
I#3 9. Suppose we want to rank the following objects in order from fastest to slowest. Assume each object is traveling at a constant speed (but not necessarily the same constant speed). Bike: 11 feet in 0. 5 second Runner: 112 feet in 7 seconds Car: 212 feet in 10 seconds Football: 52. 5 feet in 3 seconds Bird: 4. 24 feet in 0. 2 second Water Balloon: 24 feet in 1. 5 seconds a. Why is it difficult to compare the objects’ speeds based on the information given? The distances traveled and the corresponding time intervals are all different – we can’t determine which objects travel further in a fixed amount of time or which objects cover the same amount of distance in less time by simply looking at the given information. Copyright © 2013 Carlson, O’Bryan, & Joyner 78
 I#3 b. What strategy can we use to help us complete the task? We need to either determine how long it takes each object to travel some fixed distance (such as one foot) or determine how far each object travels in a given amount of time (such as one second). This latter technique is the most common convention for describing speed – we determine how far an object travels in one unit of time (in this case one second). We then apply the reasoning from this investigation. For example, the bird travels 4. 24 feet in 0. 2 (or of one second), so in one second the bird will travel 5(4. 24) = 21. 2 feet. c. Rank the objects in order from fastest to slowest. Bike (22 ft/sec), Car and Bird (21. 2 ft/sec), Football (17. 5 ft/sec), Runner and Water Balloon (16 ft/sec) Copyright © 2013 Carlson, O’Bryan, & Joyner 79
I#3 b. What strategy can we use to help us complete the task? We need to either determine how long it takes each object to travel some fixed distance (such as one foot) or determine how far each object travels in a given amount of time (such as one second). This latter technique is the most common convention for describing speed – we determine how far an object travels in one unit of time (in this case one second). We then apply the reasoning from this investigation. For example, the bird travels 4. 24 feet in 0. 2 (or of one second), so in one second the bird will travel 5(4. 24) = 21. 2 feet. c. Rank the objects in order from fastest to slowest. Bike (22 ft/sec), Car and Bird (21. 2 ft/sec), Football (17. 5 ft/sec), Runner and Water Balloon (16 ft/sec) Copyright © 2013 Carlson, O’Bryan, & Joyner 79
 I#3 10. What are the benefits of stating speeds in terms of distance traveled in one unit of time, such as 20 mph (20 miles traveled in one hour), 9. 8 m/s (9. 8 meters traveled in one second), and so on? Brainstorm some ideas with a classmate and summarize your thinking. One answer based on the results of Exercise #9 is that it makes speeds easy to compare, which is very important. For example, a car’s speedometer always reports your speed in mph (regardless of how far you travel or if you travel that speed for less than one hour) which allows you to easily compare your speed to stated speed limits. Imagine the trouble that could occur if your car instead constantly told you information such as “You just traveled 56 feet in 3. 9 seconds… 30 feet in 1. 56 seconds…” Copyright © 2013 Carlson, O’Bryan, & Joyner 80
I#3 10. What are the benefits of stating speeds in terms of distance traveled in one unit of time, such as 20 mph (20 miles traveled in one hour), 9. 8 m/s (9. 8 meters traveled in one second), and so on? Brainstorm some ideas with a classmate and summarize your thinking. One answer based on the results of Exercise #9 is that it makes speeds easy to compare, which is very important. For example, a car’s speedometer always reports your speed in mph (regardless of how far you travel or if you travel that speed for less than one hour) which allows you to easily compare your speed to stated speed limits. Imagine the trouble that could occur if your car instead constantly told you information such as “You just traveled 56 feet in 3. 9 seconds… 30 feet in 1. 56 seconds…” Copyright © 2013 Carlson, O’Bryan, & Joyner 80
 I#3 10. What are the benefits of stating speeds in terms of distance traveled in one unit of time, such as 20 mph (20 miles traveled in one hour), 9. 8 m/s (9. 8 meters traveled in one second), and so on? Brainstorm some ideas with a classmate and summarize your thinking. However, there is another important benefit that we can support with our understanding of multiplication. If we report speeds in terms of distance traveled in one unit of time, then as time elapses we can easily scale the distance by simply using multiplication. If a car travels 52 mph for 2. 1 hours, we simply multiply 52 by 2. 1 to get the distance traveled in miles (2. 1 times as long as 1 hour corresponds with 2. 1 times as far as 52 miles). If a car travels 45 mph for of an hour, we simply multiply 45 by to get the distance traveled ( times as long as 1 hour corresponds to times as far as 45 miles). The task becomes harder if a speed is reported as 3. 6 miles per 2. 7 minutes. Copyright © 2013 Carlson, O’Bryan, & Joyner 81
I#3 10. What are the benefits of stating speeds in terms of distance traveled in one unit of time, such as 20 mph (20 miles traveled in one hour), 9. 8 m/s (9. 8 meters traveled in one second), and so on? Brainstorm some ideas with a classmate and summarize your thinking. However, there is another important benefit that we can support with our understanding of multiplication. If we report speeds in terms of distance traveled in one unit of time, then as time elapses we can easily scale the distance by simply using multiplication. If a car travels 52 mph for 2. 1 hours, we simply multiply 52 by 2. 1 to get the distance traveled in miles (2. 1 times as long as 1 hour corresponds with 2. 1 times as far as 52 miles). If a car travels 45 mph for of an hour, we simply multiply 45 by to get the distance traveled ( times as long as 1 hour corresponds to times as far as 45 miles). The task becomes harder if a speed is reported as 3. 6 miles per 2. 7 minutes. Copyright © 2013 Carlson, O’Bryan, & Joyner 81
 I#3 11. Suppose that Joe is jogging at a constant speed of 0. 12 miles per minute. Let d represent the total distance (in miles) Joe has traveled during his jog and let t represent the total number of minutes he’s been jogging. a. Use ∆ notation to represent a 4 -minute time period during Joe’s jog. ∆t = 4 b. How far does Joe travel during any 4 -minute time period? Represent your answer using ∆ notation. 0. 48 miles ∆d = 0. 12(4) or ∆d = 0. 48 Copyright © 2013 Carlson, O’Bryan, & Joyner 82
I#3 11. Suppose that Joe is jogging at a constant speed of 0. 12 miles per minute. Let d represent the total distance (in miles) Joe has traveled during his jog and let t represent the total number of minutes he’s been jogging. a. Use ∆ notation to represent a 4 -minute time period during Joe’s jog. ∆t = 4 b. How far does Joe travel during any 4 -minute time period? Represent your answer using ∆ notation. 0. 48 miles ∆d = 0. 12(4) or ∆d = 0. 48 Copyright © 2013 Carlson, O’Bryan, & Joyner 82
 I#3 c. Repeat parts (a) and (b) if instead of a 4 -minute time period we look at a i) 7. 8 -minute time period a) ∆t = 7. 8 b) ∆d = 0. 12(7. 8) or ∆d = 0. 936 ii) 0. 3 -minute time period a) ∆t = 0. 3 b) ∆d = 0. 12(0. 3) or ∆d = 0. 036 iii) any x-minute time period a) ∆t = x b) ∆d = 0. 12 x Copyright © 2013 Carlson, O’Bryan, & Joyner 83
I#3 c. Repeat parts (a) and (b) if instead of a 4 -minute time period we look at a i) 7. 8 -minute time period a) ∆t = 7. 8 b) ∆d = 0. 12(7. 8) or ∆d = 0. 936 ii) 0. 3 -minute time period a) ∆t = 0. 3 b) ∆d = 0. 12(0. 3) or ∆d = 0. 036 iii) any x-minute time period a) ∆t = x b) ∆d = 0. 12 x Copyright © 2013 Carlson, O’Bryan, & Joyner 83
 I#3 d. For any change in t, what happens to the change in d? Explain, then represent your thinking using ∆ notation. The change in distance (in miles) is always 0. 12 times as large as the change in time (in minutes). ∆d = 0. 12(∆t) So far we’ve focused on the idea of constant speed. However, this is just a specific example of the more general concept of constant rate of change. Constant Rate of Change A constant rate of change of one quantity with respect to another quantity exists when, for any uniform change in one quantity’s value, the other quantity’s value changes by equal amounts. Copyright © 2013 Carlson, O’Bryan, & Joyner 84
I#3 d. For any change in t, what happens to the change in d? Explain, then represent your thinking using ∆ notation. The change in distance (in miles) is always 0. 12 times as large as the change in time (in minutes). ∆d = 0. 12(∆t) So far we’ve focused on the idea of constant speed. However, this is just a specific example of the more general concept of constant rate of change. Constant Rate of Change A constant rate of change of one quantity with respect to another quantity exists when, for any uniform change in one quantity’s value, the other quantity’s value changes by equal amounts. Copyright © 2013 Carlson, O’Bryan, & Joyner 84
 I#3 12. If we know that the total cost of purchasing a bag of walnuts increases at a rate of $7 per pound, then it’s easy to determine the change in total cost if we change the amount of walnuts we purchase. Let c represent the total cost of purchasing walnuts (in dollars) and let w represent the total weight of walnuts purchased (in pounds). a. Suppose we have some walnuts in a bag and we add 3 more pounds of walnuts to the bag. Represent the change in the number of pounds of walnuts using ∆ notation. ∆w = 3 b. How much does the total cost of the walnuts we purchase change? Represent your answer using ∆ notation. $21 ∆c = 7(3) or ∆c = 21 Copyright © 2013 Carlson, O’Bryan, & Joyner 85
I#3 12. If we know that the total cost of purchasing a bag of walnuts increases at a rate of $7 per pound, then it’s easy to determine the change in total cost if we change the amount of walnuts we purchase. Let c represent the total cost of purchasing walnuts (in dollars) and let w represent the total weight of walnuts purchased (in pounds). a. Suppose we have some walnuts in a bag and we add 3 more pounds of walnuts to the bag. Represent the change in the number of pounds of walnuts using ∆ notation. ∆w = 3 b. How much does the total cost of the walnuts we purchase change? Represent your answer using ∆ notation. $21 ∆c = 7(3) or ∆c = 21 Copyright © 2013 Carlson, O’Bryan, & Joyner 85
 I#3 c. Repeat parts (a) and (b) if instead of adding 3 more pounds of walnuts we i) add 2. 8 pounds of walnuts to the bag. a) ∆w = 2. 8 b) ∆c = 7(2. 8) or ∆c = 19. 6 ii) add 0. 65 pounds of walnuts to the bag. a) ∆w = 0. 65 b) ∆c = 7(0. 65) or ∆c = 4. 55 iii) remove 1. 2 pounds of walnuts from the bag. a) ∆w = – 1. 2 b) ∆c = 7(– 1. 2) or ∆c = – 8. 4 Copyright © 2013 Carlson, O’Bryan, & Joyner 86
I#3 c. Repeat parts (a) and (b) if instead of adding 3 more pounds of walnuts we i) add 2. 8 pounds of walnuts to the bag. a) ∆w = 2. 8 b) ∆c = 7(2. 8) or ∆c = 19. 6 ii) add 0. 65 pounds of walnuts to the bag. a) ∆w = 0. 65 b) ∆c = 7(0. 65) or ∆c = 4. 55 iii) remove 1. 2 pounds of walnuts from the bag. a) ∆w = – 1. 2 b) ∆c = 7(– 1. 2) or ∆c = – 8. 4 Copyright © 2013 Carlson, O’Bryan, & Joyner 86
 I#3 d. For any change in w, what happens to the change in c? Explain, then represent your thinking using ∆ notation. The change in total cost (in dollars) is always 7 times as large as the change in weight (in pounds). ∆c = 7(∆w) e. If your friend gives you $10 to purchase more walnuts, how many additional pounds of walnuts could you add to your bag? Approaches may vary. One example is given. Any change in 1 dollar spent on walnuts corresponds with a change of pounds of walnuts purchased. So if ∆c = 10, then You can purchase an additional 1. 43 pounds of walnuts. Copyright © 2013 Carlson, O’Bryan, & Joyner 87
I#3 d. For any change in w, what happens to the change in c? Explain, then represent your thinking using ∆ notation. The change in total cost (in dollars) is always 7 times as large as the change in weight (in pounds). ∆c = 7(∆w) e. If your friend gives you $10 to purchase more walnuts, how many additional pounds of walnuts could you add to your bag? Approaches may vary. One example is given. Any change in 1 dollar spent on walnuts corresponds with a change of pounds of walnuts purchased. So if ∆c = 10, then You can purchase an additional 1. 43 pounds of walnuts. Copyright © 2013 Carlson, O’Bryan, & Joyner 87
 I#3 13. Suppose we want to add some sand to a child’s sandbox, and that we know an 8 -liter bag of sand weighs 25. 6 pounds. Define variables to represent the quantities in this context, then represent the relationship described using ∆ notation. Answers may vary based on how we define our variables. Two possible answers are given. Method 1: Let b represent the volume of sand in the sandbox (in bags) and let w represent the weight of the sandbox (in pounds). Then ∆w = 25. 6(∆b). In other words, the change in the sandbox weight (in pounds) is always 25. 6 times as large as the change in volume of sand (in bags). Copyright © 2013 Carlson, O’Bryan, & Joyner 88
I#3 13. Suppose we want to add some sand to a child’s sandbox, and that we know an 8 -liter bag of sand weighs 25. 6 pounds. Define variables to represent the quantities in this context, then represent the relationship described using ∆ notation. Answers may vary based on how we define our variables. Two possible answers are given. Method 1: Let b represent the volume of sand in the sandbox (in bags) and let w represent the weight of the sandbox (in pounds). Then ∆w = 25. 6(∆b). In other words, the change in the sandbox weight (in pounds) is always 25. 6 times as large as the change in volume of sand (in bags). Copyright © 2013 Carlson, O’Bryan, & Joyner 88
 I#3 13. Suppose we want to add some sand to a child’s sandbox, and that we know an 8 -liter bag of sand weighs 25. 6 pounds. Define variables to represent the quantities in this context, then represent the relationship described using ∆ notation. Method 2: Let v represent the volume of sand in the sandbox (in liters) and let w represent the weight of the sandbox (in pounds). Then ∆w = 3. 2(∆v). In other words, the change in the sandbox weight (in pounds) is always 3. 2 times as large as the change in volume of sand (in liters). Copyright © 2013 Carlson, O’Bryan, & Joyner 89
I#3 13. Suppose we want to add some sand to a child’s sandbox, and that we know an 8 -liter bag of sand weighs 25. 6 pounds. Define variables to represent the quantities in this context, then represent the relationship described using ∆ notation. Method 2: Let v represent the volume of sand in the sandbox (in liters) and let w represent the weight of the sandbox (in pounds). Then ∆w = 3. 2(∆v). In other words, the change in the sandbox weight (in pounds) is always 3. 2 times as large as the change in volume of sand (in liters). Copyright © 2013 Carlson, O’Bryan, & Joyner 89
 Investigation #4
Investigation #4
 I#4 PRACTICE WITH CONSTANT RATE OF CHANGE 1. Jorge left his house to go for a jog this morning. Let d = Jorge’s distance (in miles) from his house. What’s the difference in meaning between d = 2 and ∆d = 2? d = 2 means that Jorge is 2 miles from his house. ∆d = 2 describes a change of 2 miles in the distance Jorge is from his house, such as the distance covered between the times he was 1 mile from his house (d = 1) and 3 miles from his house (d = 3). Copyright © 2013 Carlson, O’Bryan, & Joyner 91
I#4 PRACTICE WITH CONSTANT RATE OF CHANGE 1. Jorge left his house to go for a jog this morning. Let d = Jorge’s distance (in miles) from his house. What’s the difference in meaning between d = 2 and ∆d = 2? d = 2 means that Jorge is 2 miles from his house. ∆d = 2 describes a change of 2 miles in the distance Jorge is from his house, such as the distance covered between the times he was 1 mile from his house (d = 1) and 3 miles from his house (d = 3). Copyright © 2013 Carlson, O’Bryan, & Joyner 91
 I#4 2. Student Council is planning to rent a banquet hall for the post-graduation party this year. In addition to the rental costs, the hall charges $14 person for food. Let p represent the number of people who will attend the party and c represent the total cost of the party. a. What does the statement mean? The change in the total cost of the party (in dollars) is 14 times as large as the change in the number of people attending. b. If p changes by 7, by how much does c change? What does this represent? c changes by 98 since ∆p = 7 and ∆c = 14(∆p) = 14(7) = 98. If 7 additional people attend, the total cost of the party increases by $98 dollars. Copyright © 2013 Carlson, O’Bryan, & Joyner 92
I#4 2. Student Council is planning to rent a banquet hall for the post-graduation party this year. In addition to the rental costs, the hall charges $14 person for food. Let p represent the number of people who will attend the party and c represent the total cost of the party. a. What does the statement mean? The change in the total cost of the party (in dollars) is 14 times as large as the change in the number of people attending. b. If p changes by 7, by how much does c change? What does this represent? c changes by 98 since ∆p = 7 and ∆c = 14(∆p) = 14(7) = 98. If 7 additional people attend, the total cost of the party increases by $98 dollars. Copyright © 2013 Carlson, O’Bryan, & Joyner 92
 I#4 c. How much does c change by if p changes by – 5? What does this represent? c changes by – 70 since ∆p = – 5 and ∆c = 14(∆p) = 14(– 5) = – 70. If 5 fewer people decide to attend the party, the total cost will decrease by $70. d. If c changed by 182, by how much did p change? What does this represent? p changed by 13 since ∆c = 14(∆p) meaning that ∆p = (1/14)(∆c) = (1/14)(182) = 13. If the total cost of the party increased by $182, then it means 13 additional people must have decided to attend. Copyright © 2013 Carlson, O’Bryan, & Joyner 93
I#4 c. How much does c change by if p changes by – 5? What does this represent? c changes by – 70 since ∆p = – 5 and ∆c = 14(∆p) = 14(– 5) = – 70. If 5 fewer people decide to attend the party, the total cost will decrease by $70. d. If c changed by 182, by how much did p change? What does this represent? p changed by 13 since ∆c = 14(∆p) meaning that ∆p = (1/14)(∆c) = (1/14)(182) = 13. If the total cost of the party increased by $182, then it means 13 additional people must have decided to attend. Copyright © 2013 Carlson, O’Bryan, & Joyner 93
 I#4 3. Suppose we know that two variables (x and y) are related such that ∆y = – 3 ∙ ∆x. a. What does the statement ∆y = – 3 ∙ ∆x mean? The change in the value of y is always – 3 times as large as the change in the value of x. b. If x changes from x = 1 to x = 9, by how much does y change? c. How much does y change by if x changes from x = 4 to x = – 2? d. If y changes to y = 8 from y = 10, by how much does x change? Copyright © 2013 Carlson, O’Bryan, & Joyner 94
I#4 3. Suppose we know that two variables (x and y) are related such that ∆y = – 3 ∙ ∆x. a. What does the statement ∆y = – 3 ∙ ∆x mean? The change in the value of y is always – 3 times as large as the change in the value of x. b. If x changes from x = 1 to x = 9, by how much does y change? c. How much does y change by if x changes from x = 4 to x = – 2? d. If y changes to y = 8 from y = 10, by how much does x change? Copyright © 2013 Carlson, O’Bryan, & Joyner 94
 I#4 In Exercise #2 -3 we saw examples where the change in one variable always had to be some constant times as much as the change in a second variable. This is a very useful way of understanding constant rate of change. Constant Rate of Change as a Constant Multiple There exists a constant rate of change of Quantity B with respect to Quantity A if the following is always true. The constant is the number we use to describe the constant rate of change, and its value can be calculated as follows. Copyright © 2013 Carlson, O’Bryan, & Joyner 95
I#4 In Exercise #2 -3 we saw examples where the change in one variable always had to be some constant times as much as the change in a second variable. This is a very useful way of understanding constant rate of change. Constant Rate of Change as a Constant Multiple There exists a constant rate of change of Quantity B with respect to Quantity A if the following is always true. The constant is the number we use to describe the constant rate of change, and its value can be calculated as follows. Copyright © 2013 Carlson, O’Bryan, & Joyner 95
 I#4 Example 1: Suppose x is the value of quantity A and y is the value of quantity B. Then there is a constant rate of change of m between the quantities if where m is a constant, and Example 2: Each of the following represents a situation with a constant rate of change of one quantity with respect to another. Copyright © 2013 Carlson, O’Bryan, & Joyner 96
I#4 Example 1: Suppose x is the value of quantity A and y is the value of quantity B. Then there is a constant rate of change of m between the quantities if where m is a constant, and Example 2: Each of the following represents a situation with a constant rate of change of one quantity with respect to another. Copyright © 2013 Carlson, O’Bryan, & Joyner 96
 I#4 4. Use the following graphs and the given information to answer the questions that follow. a. For the graph on the left, if x changes from the given point to x = 0, by how much does y change if ? Copyright © 2013 Carlson, O’Bryan, & Joyner 97
I#4 4. Use the following graphs and the given information to answer the questions that follow. a. For the graph on the left, if x changes from the given point to x = 0, by how much does y change if ? Copyright © 2013 Carlson, O’Bryan, & Joyner 97
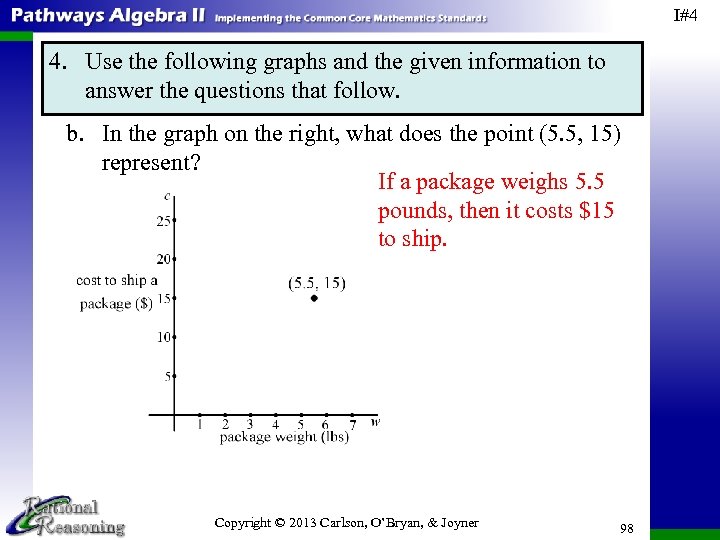 I#4 4. Use the following graphs and the given information to answer the questions that follow. b. In the graph on the right, what does the point (5. 5, 15) represent? If a package weighs 5. 5 pounds, then it costs $15 to ship. Copyright © 2013 Carlson, O’Bryan, & Joyner 98
I#4 4. Use the following graphs and the given information to answer the questions that follow. b. In the graph on the right, what does the point (5. 5, 15) represent? If a package weighs 5. 5 pounds, then it costs $15 to ship. Copyright © 2013 Carlson, O’Bryan, & Joyner 98
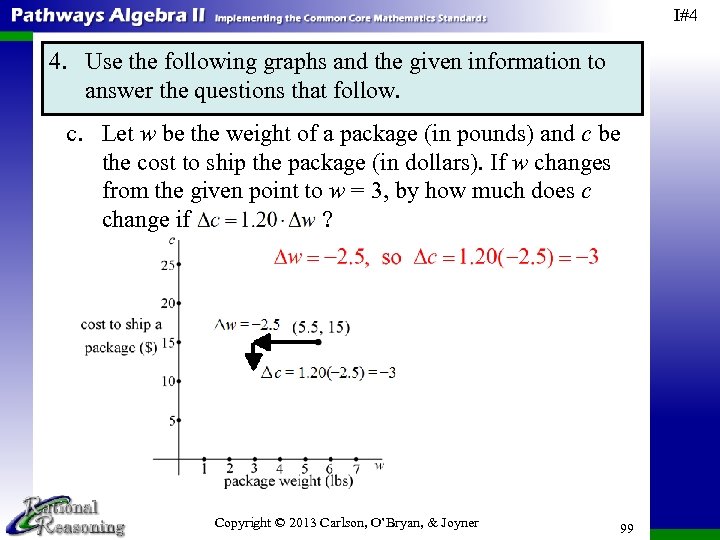 I#4 4. Use the following graphs and the given information to answer the questions that follow. c. Let w be the weight of a package (in pounds) and c be the cost to ship the package (in dollars). If w changes from the given point to w = 3, by how much does c change if ? Copyright © 2013 Carlson, O’Bryan, & Joyner 99
I#4 4. Use the following graphs and the given information to answer the questions that follow. c. Let w be the weight of a package (in pounds) and c be the cost to ship the package (in dollars). If w changes from the given point to w = 3, by how much does c change if ? Copyright © 2013 Carlson, O’Bryan, & Joyner 99
 I#4 4. Use the following graphs and the given information to answer the questions that follow. d. Explain the meaning of your answer to part (c). If we reduce the weight of the package by 2. 5 pounds, the cost to ship the package decreases by $3. Copyright © 2013 Carlson, O’Bryan, & Joyner 100
I#4 4. Use the following graphs and the given information to answer the questions that follow. d. Explain the meaning of your answer to part (c). If we reduce the weight of the package by 2. 5 pounds, the cost to ship the package decreases by $3. Copyright © 2013 Carlson, O’Bryan, & Joyner 100
 I#4 In Exercises #5 -6, explain why each context does not have a constant rate of change. (Hint: You should first identify what quantities are changing together. ) 5. When Marcus was born he was 19 inches tall. When he turned 16 he was 65 inches tall. Let h represent Marcus’s height (in inches) and let t represent his age (in years). Then ∆h is the change in Marcus’s height (in inches) and ∆t is the change in his age (in years). No constant rate of change exists in this context because, for uniform changes in his age, we do not expect to observe equal changes in his height. For example, we don’t expect his height to change the same from 1 to 4 years old as from 10 to 13 years old. Copyright © 2013 Carlson, O’Bryan, & Joyner 101
I#4 In Exercises #5 -6, explain why each context does not have a constant rate of change. (Hint: You should first identify what quantities are changing together. ) 5. When Marcus was born he was 19 inches tall. When he turned 16 he was 65 inches tall. Let h represent Marcus’s height (in inches) and let t represent his age (in years). Then ∆h is the change in Marcus’s height (in inches) and ∆t is the change in his age (in years). No constant rate of change exists in this context because, for uniform changes in his age, we do not expect to observe equal changes in his height. For example, we don’t expect his height to change the same from 1 to 4 years old as from 10 to 13 years old. Copyright © 2013 Carlson, O’Bryan, & Joyner 101
 I#4 6. The number of people following one celebrity’s Twitter feed doubled every day for a week after she appeared on Saturday Night Live. Let n represent the total number of people following the celebrity’s Twitter feed and let d be the number of days since she appeared on Saturday Night Live. Then ∆n is the change in the number of people following the celebrity’s Twitter feed and ∆d is the change in the number of days since she appeared on Saturday Night Live. Doubling does NOT produce a constant rate of change. For example, if she began with 1, 000 Twitter followers, her total number of followers after the next several days would be 2, 000 then 4, 000 then 8, 000, and it’s clear that ∆d isn’t constant for a given ∆d (such as ∆d = 1). Copyright © 2013 Carlson, O’Bryan, & Joyner 102
I#4 6. The number of people following one celebrity’s Twitter feed doubled every day for a week after she appeared on Saturday Night Live. Let n represent the total number of people following the celebrity’s Twitter feed and let d be the number of days since she appeared on Saturday Night Live. Then ∆n is the change in the number of people following the celebrity’s Twitter feed and ∆d is the change in the number of days since she appeared on Saturday Night Live. Doubling does NOT produce a constant rate of change. For example, if she began with 1, 000 Twitter followers, her total number of followers after the next several days would be 2, 000 then 4, 000 then 8, 000, and it’s clear that ∆d isn’t constant for a given ∆d (such as ∆d = 1). Copyright © 2013 Carlson, O’Bryan, & Joyner 102
 I#4 Describing a Constant Rate of Change Sometimes you might see a phrase like “There is a constant rate of change of y with respect to x. ” This just means that there is a constant m such that . 7. While performing a backup for her computer, Elise noticed that during a certain interval of time the computer was transferring data at a constant rate of 8 megabytes per second. Complete the following statement and explain what it tells us. where ∆t represents the change in the elapsed time for the backup and ∆n the change in the number of megabytes transferred. Copyright © 2013 Carlson, O’Bryan, & Joyner 103
I#4 Describing a Constant Rate of Change Sometimes you might see a phrase like “There is a constant rate of change of y with respect to x. ” This just means that there is a constant m such that . 7. While performing a backup for her computer, Elise noticed that during a certain interval of time the computer was transferring data at a constant rate of 8 megabytes per second. Complete the following statement and explain what it tells us. where ∆t represents the change in the elapsed time for the backup and ∆n the change in the number of megabytes transferred. Copyright © 2013 Carlson, O’Bryan, & Joyner 103
 I#4 7. While performing a backup for her computer, Elise noticed that during a certain interval of time the computer was transferring data at a constant rate of 8 megabytes per second. Complete the following statement and explain what it tells us. where ∆t represents the change in the elapsed time for the backup and ∆n the change in the number of megabytes transferred. The change in the total data transferred (in megabytes) was 8 times as large as the change in time (in seconds) during any portion of the given time period. Copyright © 2013 Carlson, O’Bryan, & Joyner 104
I#4 7. While performing a backup for her computer, Elise noticed that during a certain interval of time the computer was transferring data at a constant rate of 8 megabytes per second. Complete the following statement and explain what it tells us. where ∆t represents the change in the elapsed time for the backup and ∆n the change in the number of megabytes transferred. The change in the total data transferred (in megabytes) was 8 times as large as the change in time (in seconds) during any portion of the given time period. Copyright © 2013 Carlson, O’Bryan, & Joyner 104
 I#4 8. The cost of covering an area with a certain type of concrete paver increases at a constant rate of $4. 50 per square foot with respect to the size of the area covered. Complete the following statement and explain what it tells us. where ∆a represents the change in the size of the area covered (in square feet) and ∆c represents the change in the total cost of covering the area. Copyright © 2013 Carlson, O’Bryan, & Joyner 105
I#4 8. The cost of covering an area with a certain type of concrete paver increases at a constant rate of $4. 50 per square foot with respect to the size of the area covered. Complete the following statement and explain what it tells us. where ∆a represents the change in the size of the area covered (in square feet) and ∆c represents the change in the total cost of covering the area. Copyright © 2013 Carlson, O’Bryan, & Joyner 105
 I#4 8. The cost of covering an area with a certain type of concrete paver increases at a constant rate of $4. 50 per square foot with respect to the size of the area covered. Complete the following statement and explain what it tells us. where ∆a represents the change in the size of the area covered (in square feet) and ∆c represents the change in the total cost of covering the area. The change in the total cost of covering the area (in dollars) is 4. 50 times as large as the change in the area covered (in square feet). Copyright © 2013 Carlson, O’Bryan, & Joyner 106
I#4 8. The cost of covering an area with a certain type of concrete paver increases at a constant rate of $4. 50 per square foot with respect to the size of the area covered. Complete the following statement and explain what it tells us. where ∆a represents the change in the size of the area covered (in square feet) and ∆c represents the change in the total cost of covering the area. The change in the total cost of covering the area (in dollars) is 4. 50 times as large as the change in the area covered (in square feet). Copyright © 2013 Carlson, O’Bryan, & Joyner 106
 I#4 9. Suppose we know that for some constant m, and we are given the information in the following table. What is the value of m? x – 2 1 6 y 2 6. 5 14 We just need to take two entries in the table and calculate ∆x and ∆y. For example, suppose we select (– 2 , 2) and (6, 14). 14 26 Then and , so You will get the same result for any two points you choose because there is a constant rate of change. Copyright © 2013 Carlson, O’Bryan, & Joyner 107
I#4 9. Suppose we know that for some constant m, and we are given the information in the following table. What is the value of m? x – 2 1 6 y 2 6. 5 14 We just need to take two entries in the table and calculate ∆x and ∆y. For example, suppose we select (– 2 , 2) and (6, 14). 14 26 Then and , so You will get the same result for any two points you choose because there is a constant rate of change. Copyright © 2013 Carlson, O’Bryan, & Joyner 107
 I#4 10. Suppose we know that for some constant m, and we are given the information in the following graph. What is the value of m and what does it tell us about how x and y change together? We use the points on the graph to determine ∆x and ∆y. So and , and thus The change in the value of y is always – 0. 8 times as large as the change in the value of x. Copyright © 2013 Carlson, O’Bryan, & Joyner 108
I#4 10. Suppose we know that for some constant m, and we are given the information in the following graph. What is the value of m and what does it tell us about how x and y change together? We use the points on the graph to determine ∆x and ∆y. So and , and thus The change in the value of y is always – 0. 8 times as large as the change in the value of x. Copyright © 2013 Carlson, O’Bryan, & Joyner 108
 I#4 11. Suppose we know that for some constant m, and we know that two ordered pairs are (– 5, 1) and (– 3, 9). What is the value of m? We use the ordered pairs to determine ∆x and ∆y. So and , and thus The change in the value of y is always 4 times as large as the change in the value of x. Copyright © 2013 Carlson, O’Bryan, & Joyner 109
I#4 11. Suppose we know that for some constant m, and we know that two ordered pairs are (– 5, 1) and (– 3, 9). What is the value of m? We use the ordered pairs to determine ∆x and ∆y. So and , and thus The change in the value of y is always 4 times as large as the change in the value of x. Copyright © 2013 Carlson, O’Bryan, & Joyner 109
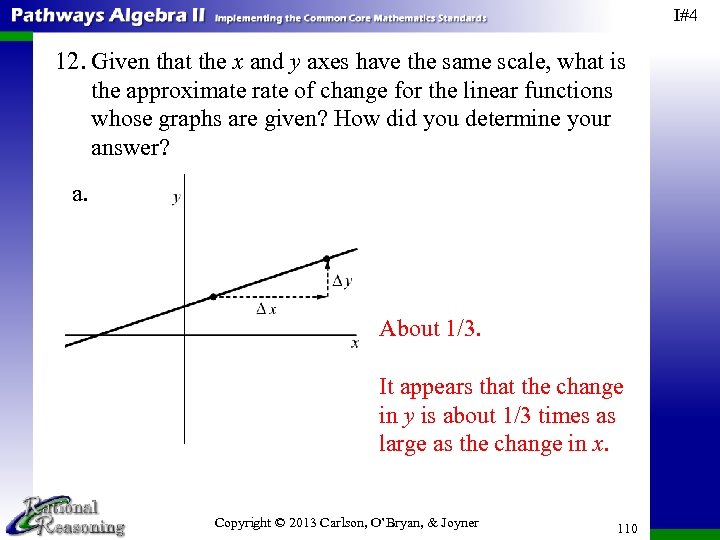 I#4 12. Given that the x and y axes have the same scale, what is the approximate rate of change for the linear functions whose graphs are given? How did you determine your answer? a. About 1/3. It appears that the change in y is about 1/3 times as large as the change in x. Copyright © 2013 Carlson, O’Bryan, & Joyner 110
I#4 12. Given that the x and y axes have the same scale, what is the approximate rate of change for the linear functions whose graphs are given? How did you determine your answer? a. About 1/3. It appears that the change in y is about 1/3 times as large as the change in x. Copyright © 2013 Carlson, O’Bryan, & Joyner 110
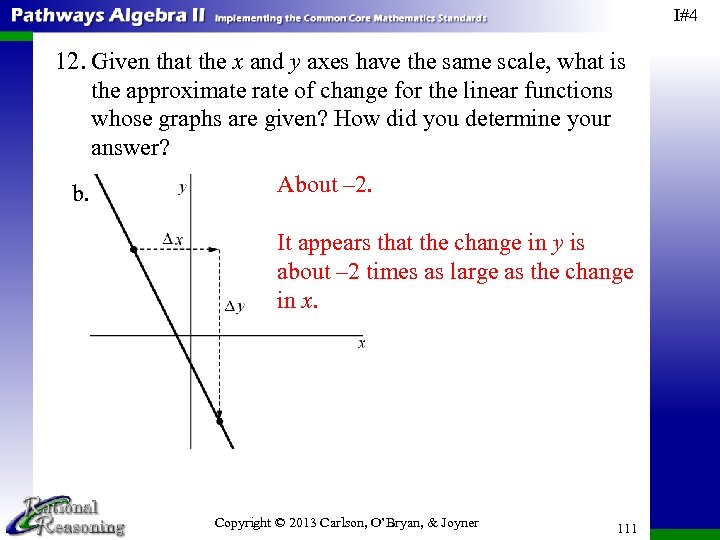 I#4 12. Given that the x and y axes have the same scale, what is the approximate rate of change for the linear functions whose graphs are given? How did you determine your answer? b. About – 2. It appears that the change in y is about – 2 times as large as the change in x. Copyright © 2013 Carlson, O’Bryan, & Joyner 111
I#4 12. Given that the x and y axes have the same scale, what is the approximate rate of change for the linear functions whose graphs are given? How did you determine your answer? b. About – 2. It appears that the change in y is about – 2 times as large as the change in x. Copyright © 2013 Carlson, O’Bryan, & Joyner 111
 Investigation #5
Investigation #5
 I#5 APPLYING CONSTANT RATE OF CHANGE TO FIND NEW VALUES 1. Suppose that we know that ∆y = m ∙ ∆x for some constant m, and we are given the information in the following table. What is the value of m and what does it tells us about how x and y change together? x – 7 – 4 1 y 15 9 – 17 We just need to take two entries in the table and calculate ∆x and ∆y. For example, suppose we select (– 4, 9) and (1, – 1). Then ∆x = 5 and ∆y = – 10, so The change in the value of y is always – 2 times as large as the change in the value of x. Copyright © 2013 Carlson, O’Bryan, & Joyner 113
I#5 APPLYING CONSTANT RATE OF CHANGE TO FIND NEW VALUES 1. Suppose that we know that ∆y = m ∙ ∆x for some constant m, and we are given the information in the following table. What is the value of m and what does it tells us about how x and y change together? x – 7 – 4 1 y 15 9 – 17 We just need to take two entries in the table and calculate ∆x and ∆y. For example, suppose we select (– 4, 9) and (1, – 1). Then ∆x = 5 and ∆y = – 10, so The change in the value of y is always – 2 times as large as the change in the value of x. Copyright © 2013 Carlson, O’Bryan, & Joyner 113
 I#5 For Exercises #2 -4, suppose we know that the changes in the values of two variables are related according to ∆y = 4 ∙ ∆x. 2 a. If we start off at x = 7 and let x change to be x = 10, what is the change in x? b. By how much does y change for the change in x you found in part (a)? c. Suppose we know that y = 15 when x = 7. What is the value of y when x = 10? How did you find this? We find this by adding the change in y to the starting value of y. Copyright © 2013 Carlson, O’Bryan, & Joyner 114
I#5 For Exercises #2 -4, suppose we know that the changes in the values of two variables are related according to ∆y = 4 ∙ ∆x. 2 a. If we start off at x = 7 and let x change to be x = 10, what is the change in x? b. By how much does y change for the change in x you found in part (a)? c. Suppose we know that y = 15 when x = 7. What is the value of y when x = 10? How did you find this? We find this by adding the change in y to the starting value of y. Copyright © 2013 Carlson, O’Bryan, & Joyner 114
 I#5 For Exercises #2 -4, suppose we know that the changes in the values of two variables are related according to ∆y = 4 ∙ ∆x. 3 a. If we end at x = 12 after starting at x = 7, what is the change in x? b. By how much does y change for the change in x you found in part (a)? c. Suppose we know that y = 15 when x = 7. What is the value of y when x = 12? Copyright © 2013 Carlson, O’Bryan, & Joyner 115
I#5 For Exercises #2 -4, suppose we know that the changes in the values of two variables are related according to ∆y = 4 ∙ ∆x. 3 a. If we end at x = 12 after starting at x = 7, what is the change in x? b. By how much does y change for the change in x you found in part (a)? c. Suppose we know that y = 15 when x = 7. What is the value of y when x = 12? Copyright © 2013 Carlson, O’Bryan, & Joyner 115
 I#5 For Exercises #2 -4, suppose we know that the changes in the values of two variables are related according to ∆y = 4 ∙ ∆x. 4 a. If we start off at x = 7 and let x change to be x = 4, what is the change in x? b. By how much does y change for the change in x you found in part (a)? c. Suppose we know that y = 15 when x = 7. What is the value of y when x = 4? Copyright © 2013 Carlson, O’Bryan, & Joyner 116
I#5 For Exercises #2 -4, suppose we know that the changes in the values of two variables are related according to ∆y = 4 ∙ ∆x. 4 a. If we start off at x = 7 and let x change to be x = 4, what is the change in x? b. By how much does y change for the change in x you found in part (a)? c. Suppose we know that y = 15 when x = 7. What is the value of y when x = 4? Copyright © 2013 Carlson, O’Bryan, & Joyner 116
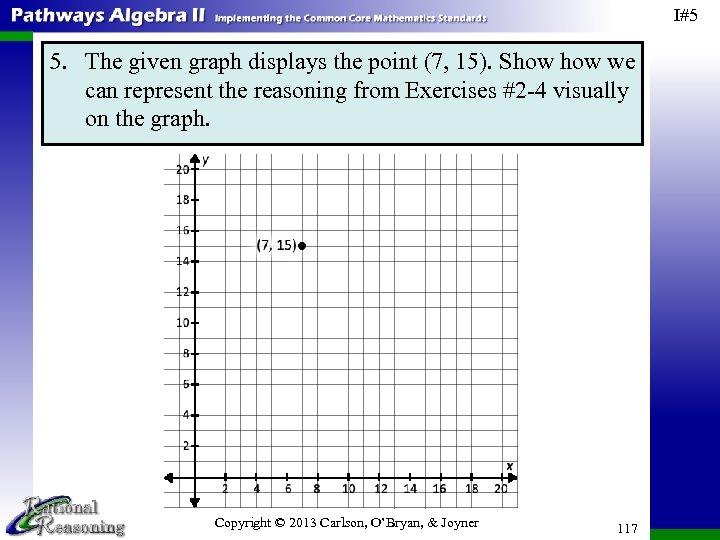 I#5 5. The given graph displays the point (7, 15). Show we can represent the reasoning from Exercises #2 -4 visually on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 117
I#5 5. The given graph displays the point (7, 15). Show we can represent the reasoning from Exercises #2 -4 visually on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 117
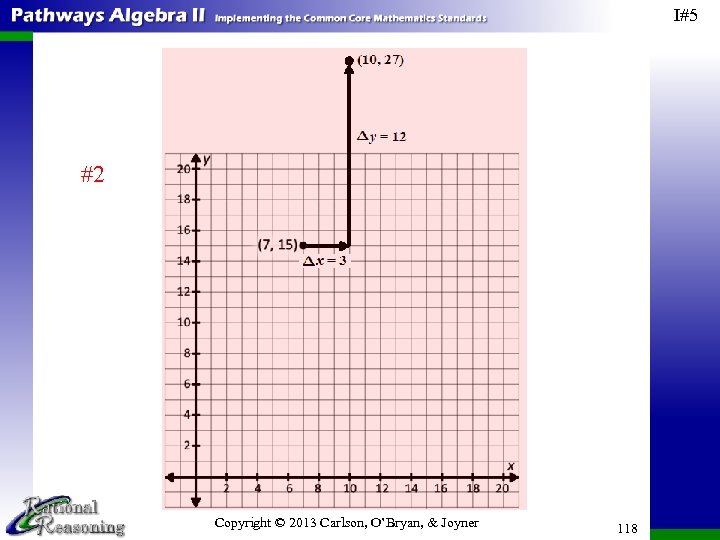 I#5 #2 Copyright © 2013 Carlson, O’Bryan, & Joyner 118
I#5 #2 Copyright © 2013 Carlson, O’Bryan, & Joyner 118
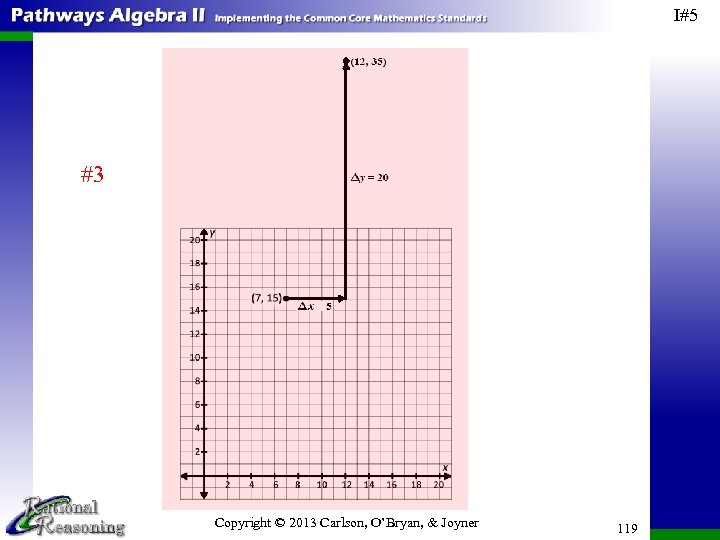 I#5 #3 Copyright © 2013 Carlson, O’Bryan, & Joyner 119
I#5 #3 Copyright © 2013 Carlson, O’Bryan, & Joyner 119
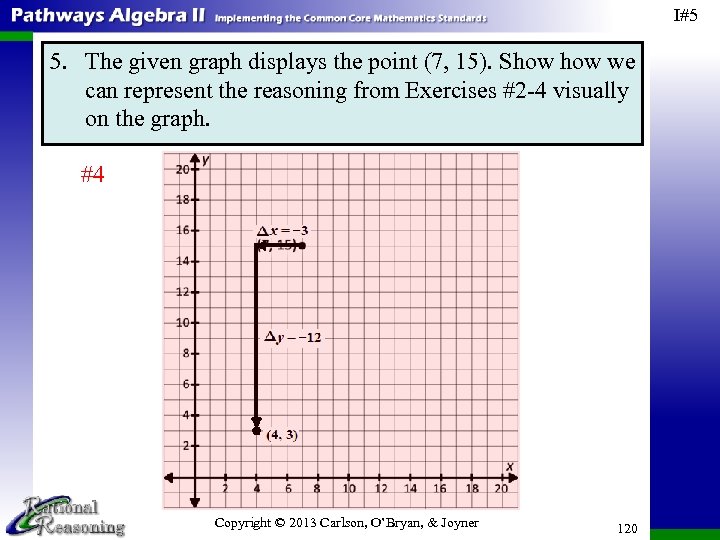 I#5 5. The given graph displays the point (7, 15). Show we can represent the reasoning from Exercises #2 -4 visually on the graph. #4 Copyright © 2013 Carlson, O’Bryan, & Joyner 120
I#5 5. The given graph displays the point (7, 15). Show we can represent the reasoning from Exercises #2 -4 visually on the graph. #4 Copyright © 2013 Carlson, O’Bryan, & Joyner 120
 I#5 6. Apply your understanding of constant rate of change to complete the following table of values given that ∆y = 4 ∙ ∆x. Hint: Your first step should be to determine the change in x from one value to another value. x – 2 5 7 9. 5 y For a given x-value, we find the change in x away from 7. 15 For example, to get from x = 7 to x = – 2 we must change x by – 9 (that is, ∆x = – 9). Then ∆y = 4 ∙ ∆x = 4 ∙ (– 9) = – 36, so we change y by – 36 from y = 15 to get y = – 21. Copyright © 2013 Carlson, O’Bryan, & Joyner 121
I#5 6. Apply your understanding of constant rate of change to complete the following table of values given that ∆y = 4 ∙ ∆x. Hint: Your first step should be to determine the change in x from one value to another value. x – 2 5 7 9. 5 y For a given x-value, we find the change in x away from 7. 15 For example, to get from x = 7 to x = – 2 we must change x by – 9 (that is, ∆x = – 9). Then ∆y = 4 ∙ ∆x = 4 ∙ (– 9) = – 36, so we change y by – 36 from y = 15 to get y = – 21. Copyright © 2013 Carlson, O’Bryan, & Joyner 121
 I#5 6. Apply your understanding of constant rate of change to complete the following table of values given that ∆y = 4 ∙ ∆x. Hint: Your first step should be to determine the change in x from one value to another value. x – 2 5 7 9. 5 y – 21 For a given x-value, we find the change in x away from 7. 15 For example, to get from x = 7 to x = – 2 we must change x by – 9 (that is, ∆x = – 9). Then ∆y = 4 ∙ ∆x = 4 ∙ (– 9) = – 36, so we change y by – 36 from y = 15 to get y = – 21. Copyright © 2013 Carlson, O’Bryan, & Joyner 122
I#5 6. Apply your understanding of constant rate of change to complete the following table of values given that ∆y = 4 ∙ ∆x. Hint: Your first step should be to determine the change in x from one value to another value. x – 2 5 7 9. 5 y – 21 For a given x-value, we find the change in x away from 7. 15 For example, to get from x = 7 to x = – 2 we must change x by – 9 (that is, ∆x = – 9). Then ∆y = 4 ∙ ∆x = 4 ∙ (– 9) = – 36, so we change y by – 36 from y = 15 to get y = – 21. Copyright © 2013 Carlson, O’Bryan, & Joyner 122
 I#5 6. Apply your understanding of constant rate of change to complete the following table of values given that ∆y = 4 ∙ ∆x. Hint: Your first step should be to determine the change in x from one value to another value. x – 2 5 7 y – 21 7 15 9. 5 25 For a given x-value, we find the change in x away from 7. For example, to get from x = 7 to x = – 2 we must change x by – 9 (that is, ∆x = – 9). Then ∆y = 4 ∙ ∆x = 4 ∙ (– 9) = – 36, so we change y by – 36 from y = 15 to get y = – 21. Repeat for all values of x in the table. Copyright © 2013 Carlson, O’Bryan, & Joyner 123
I#5 6. Apply your understanding of constant rate of change to complete the following table of values given that ∆y = 4 ∙ ∆x. Hint: Your first step should be to determine the change in x from one value to another value. x – 2 5 7 y – 21 7 15 9. 5 25 For a given x-value, we find the change in x away from 7. For example, to get from x = 7 to x = – 2 we must change x by – 9 (that is, ∆x = – 9). Then ∆y = 4 ∙ ∆x = 4 ∙ (– 9) = – 36, so we change y by – 36 from y = 15 to get y = – 21. Repeat for all values of x in the table. Copyright © 2013 Carlson, O’Bryan, & Joyner 123
 I#5 In Exercises #2 -6 we thought about how to find a new value for y by applying our understanding of constant rate of change. We started by finding a change in the value of x, then used our constant rate of change to determine the corresponding change in the value of y. Finally we used this change in y to find a final (new) value for y. Use this technique and reasoning to complete the remaining tasks in this investigation. Copyright © 2013 Carlson, O’Bryan, & Joyner 124
I#5 In Exercises #2 -6 we thought about how to find a new value for y by applying our understanding of constant rate of change. We started by finding a change in the value of x, then used our constant rate of change to determine the corresponding change in the value of y. Finally we used this change in y to find a final (new) value for y. Use this technique and reasoning to complete the remaining tasks in this investigation. Copyright © 2013 Carlson, O’Bryan, & Joyner 124
 I#5 7. Suppose you are considering shipping a package with a certain shipping company. Let w represent the weight of the package (in pounds) and let c represent the cost of shipping the package (in dollars). Furthermore, suppose c = 15 when w = 5. 5 and that ∆c = 1. 20 ∙ ∆w. a. What is the value of c when w = 7. 5? What does this tell us? ∆w = 2 from w = 5. 5 to w = 7. 5, so ∆c = 1. 20(2) = 2. 40, and thus c = 2. 40 + 15 = 17. 40 when w = 7. 5. The cost to ship a package weighing 7. 5 pounds is $17. 40. Copyright © 2013 Carlson, O’Bryan, & Joyner 125
I#5 7. Suppose you are considering shipping a package with a certain shipping company. Let w represent the weight of the package (in pounds) and let c represent the cost of shipping the package (in dollars). Furthermore, suppose c = 15 when w = 5. 5 and that ∆c = 1. 20 ∙ ∆w. a. What is the value of c when w = 7. 5? What does this tell us? ∆w = 2 from w = 5. 5 to w = 7. 5, so ∆c = 1. 20(2) = 2. 40, and thus c = 2. 40 + 15 = 17. 40 when w = 7. 5. The cost to ship a package weighing 7. 5 pounds is $17. 40. Copyright © 2013 Carlson, O’Bryan, & Joyner 125
 I#5 7. Suppose you are considering shipping a package with a certain shipping company. Let w represent the weight of the package (in pounds) and let c represent the cost of shipping the package (in dollars). Furthermore, suppose c = 15 when w = 5. 5 and that ∆c = 1. 20 ∙ ∆w. b. What is the value of c when w = 0? What does this tell us? ∆w = – 5. 5 from w = 5. 5 to w = 0, so ∆c = 1. 20(– 5. 5) = – 6. 60, and thus c = – 6. 60 + 15 = 8. 40 when w = 0. The fixed cost to ship a package (prior to determining the weight and adding the corresponding additional costs) is $8. 40. Copyright © 2013 Carlson, O’Bryan, & Joyner 126
I#5 7. Suppose you are considering shipping a package with a certain shipping company. Let w represent the weight of the package (in pounds) and let c represent the cost of shipping the package (in dollars). Furthermore, suppose c = 15 when w = 5. 5 and that ∆c = 1. 20 ∙ ∆w. b. What is the value of c when w = 0? What does this tell us? ∆w = – 5. 5 from w = 5. 5 to w = 0, so ∆c = 1. 20(– 5. 5) = – 6. 60, and thus c = – 6. 60 + 15 = 8. 40 when w = 0. The fixed cost to ship a package (prior to determining the weight and adding the corresponding additional costs) is $8. 40. Copyright © 2013 Carlson, O’Bryan, & Joyner 126
 I#5 6. Given that ∆r = – 1. 25 ∙ ∆h, complete the following table of values. h – 4 4 6 18 r 6 For a given h-value, we find the change in h away from 4. For example, to get from h = 4 to h = 6 we must change h by 2 (that is, ∆h = 2). Then ∆r = – 1. 25 ∙ ∆h = – 1. 25 ∙ (2) = – 2. 5, so we change r by – 2. 5 from r = 6 to get r = 3. 5. Copyright © 2013 Carlson, O’Bryan, & Joyner 127
I#5 6. Given that ∆r = – 1. 25 ∙ ∆h, complete the following table of values. h – 4 4 6 18 r 6 For a given h-value, we find the change in h away from 4. For example, to get from h = 4 to h = 6 we must change h by 2 (that is, ∆h = 2). Then ∆r = – 1. 25 ∙ ∆h = – 1. 25 ∙ (2) = – 2. 5, so we change r by – 2. 5 from r = 6 to get r = 3. 5. Copyright © 2013 Carlson, O’Bryan, & Joyner 127
 I#5 6. Given that ∆r = – 1. 25 ∙ ∆h, complete the following table of values. h – 4 4 6 18 r 6 3. 5 For a given h-value, we find the change in h away from 4. For example, to get from h = 4 to h = 6 we must change h by 2 (that is, ∆h = 2). Then ∆r = – 1. 25 ∙ ∆h = – 1. 25 ∙ (2) = – 2. 5, so we change r by – 2. 5 from r = 6 to get r = 3. 5. Copyright © 2013 Carlson, O’Bryan, & Joyner 128
I#5 6. Given that ∆r = – 1. 25 ∙ ∆h, complete the following table of values. h – 4 4 6 18 r 6 3. 5 For a given h-value, we find the change in h away from 4. For example, to get from h = 4 to h = 6 we must change h by 2 (that is, ∆h = 2). Then ∆r = – 1. 25 ∙ ∆h = – 1. 25 ∙ (2) = – 2. 5, so we change r by – 2. 5 from r = 6 to get r = 3. 5. Copyright © 2013 Carlson, O’Bryan, & Joyner 128
 I#5 6. Given that ∆r = – 1. 25 ∙ ∆h, complete the following table of values. h – 4 4 6 r 16 6 3. 5 18 – 11. 5 For a given h-value, we find the change in h away from 4. For example, to get from h = 4 to h = 6 we must change h by 2 (that is, ∆h = 2). Then ∆r = – 1. 25 ∙ ∆h = – 1. 25 ∙ (2) = – 2. 5, so we change r by – 2. 5 from r = 6 to get r = 3. 5. Repeat for all values of h in the table. Copyright © 2013 Carlson, O’Bryan, & Joyner 129
I#5 6. Given that ∆r = – 1. 25 ∙ ∆h, complete the following table of values. h – 4 4 6 r 16 6 3. 5 18 – 11. 5 For a given h-value, we find the change in h away from 4. For example, to get from h = 4 to h = 6 we must change h by 2 (that is, ∆h = 2). Then ∆r = – 1. 25 ∙ ∆h = – 1. 25 ∙ (2) = – 2. 5, so we change r by – 2. 5 from r = 6 to get r = 3. 5. Repeat for all values of h in the table. Copyright © 2013 Carlson, O’Bryan, & Joyner 129
 I#5 Linear Function If there is a constant rate of change of one quantity with respect to another quantity, then we say that the relationship is a linear function. Example 1: Suppose ∆y = 2 ∙ ∆x. Then we say that “y is a linear function of x. ” Example 2: Suppose a car is traveling at 50 mph. Let d represent the distance the car has traveled from some location (in miles) and t represent the corresponding elapsed time (in hours) since leaving the location, then ∆d = 50 ∙ ∆t. Then we say that “the distance traveled is a linear function of the time elapsed. ” Copyright © 2013 Carlson, O’Bryan, & Joyner 130
I#5 Linear Function If there is a constant rate of change of one quantity with respect to another quantity, then we say that the relationship is a linear function. Example 1: Suppose ∆y = 2 ∙ ∆x. Then we say that “y is a linear function of x. ” Example 2: Suppose a car is traveling at 50 mph. Let d represent the distance the car has traveled from some location (in miles) and t represent the corresponding elapsed time (in hours) since leaving the location, then ∆d = 50 ∙ ∆t. Then we say that “the distance traveled is a linear function of the time elapsed. ” Copyright © 2013 Carlson, O’Bryan, & Joyner 130
 I#5 9. Use the given graph to answer the questions that follow given that ∆y = ∆x. a. What is the value of y when x = 3. 5? Represent your reasoning on the graph. b. What is the value of y when x = – 4? Represent your reasoning on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 131
I#5 9. Use the given graph to answer the questions that follow given that ∆y = ∆x. a. What is the value of y when x = 3. 5? Represent your reasoning on the graph. b. What is the value of y when x = – 4? Represent your reasoning on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 131
 I#5 9. Use the given graph to answer the questions that follow given that ∆y = ∆x. a. What is the value of y when x = 3. 5? Represent your reasoning on the graph. From the reference point (1, 2), ∆x = 2. 5, so ∆y = 2. 5, and thus y = 2. 5 + 2 = 4. 5. b. What is the value of y when x = – 4? Represent your reasoning on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 132
I#5 9. Use the given graph to answer the questions that follow given that ∆y = ∆x. a. What is the value of y when x = 3. 5? Represent your reasoning on the graph. From the reference point (1, 2), ∆x = 2. 5, so ∆y = 2. 5, and thus y = 2. 5 + 2 = 4. 5. b. What is the value of y when x = – 4? Represent your reasoning on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 132
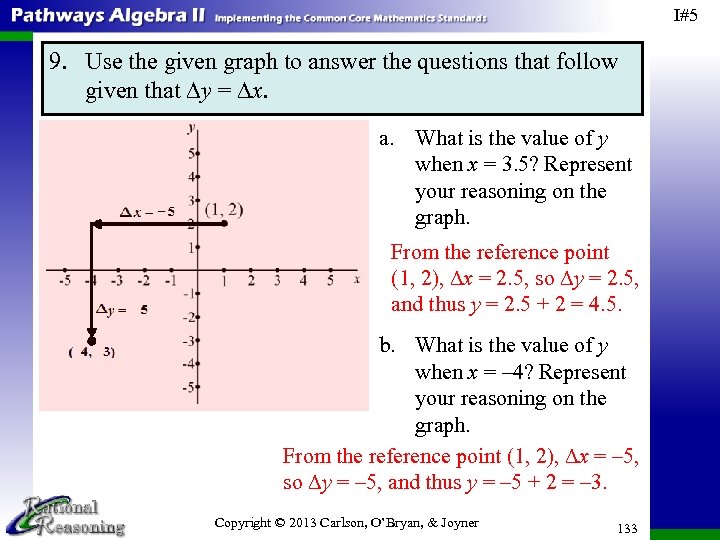 I#5 9. Use the given graph to answer the questions that follow given that ∆y = ∆x. a. What is the value of y when x = 3. 5? Represent your reasoning on the graph. From the reference point (1, 2), ∆x = 2. 5, so ∆y = 2. 5, and thus y = 2. 5 + 2 = 4. 5. b. What is the value of y when x = – 4? Represent your reasoning on the graph. From the reference point (1, 2), ∆x = – 5, so ∆y = – 5, and thus y = – 5 + 2 = – 3. Copyright © 2013 Carlson, O’Bryan, & Joyner 133
I#5 9. Use the given graph to answer the questions that follow given that ∆y = ∆x. a. What is the value of y when x = 3. 5? Represent your reasoning on the graph. From the reference point (1, 2), ∆x = 2. 5, so ∆y = 2. 5, and thus y = 2. 5 + 2 = 4. 5. b. What is the value of y when x = – 4? Represent your reasoning on the graph. From the reference point (1, 2), ∆x = – 5, so ∆y = – 5, and thus y = – 5 + 2 = – 3. Copyright © 2013 Carlson, O’Bryan, & Joyner 133
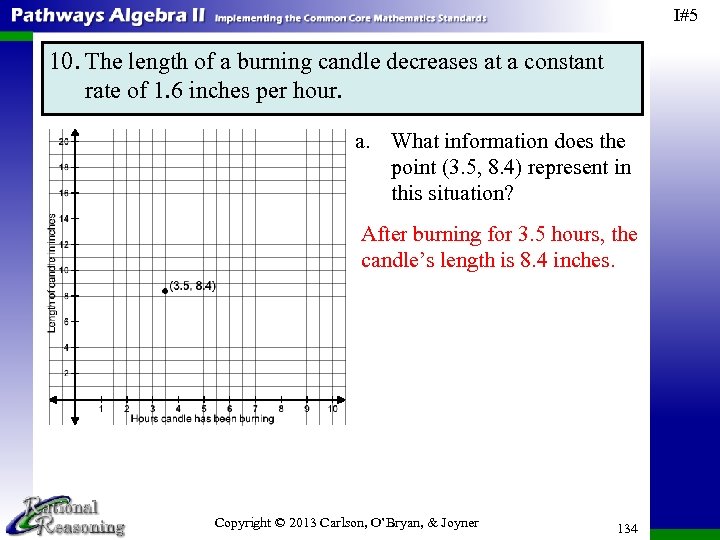 I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. a. What information does the point (3. 5, 8. 4) represent in this situation? After burning for 3. 5 hours, the candle’s length is 8. 4 inches. Copyright © 2013 Carlson, O’Bryan, & Joyner 134
I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. a. What information does the point (3. 5, 8. 4) represent in this situation? After burning for 3. 5 hours, the candle’s length is 8. 4 inches. Copyright © 2013 Carlson, O’Bryan, & Joyner 134
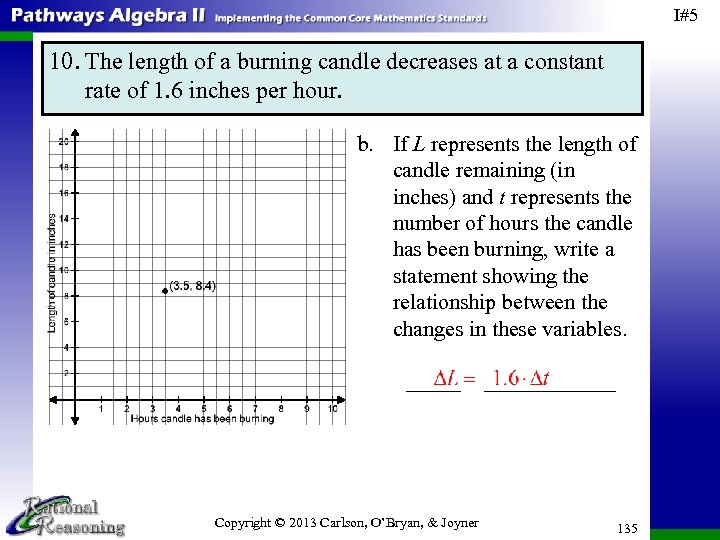 I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. b. If L represents the length of candle remaining (in inches) and t represents the number of hours the candle has been burning, write a statement showing the relationship between the changes in these variables. _____ = ______ Copyright © 2013 Carlson, O’Bryan, & Joyner 135
I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. b. If L represents the length of candle remaining (in inches) and t represents the number of hours the candle has been burning, write a statement showing the relationship between the changes in these variables. _____ = ______ Copyright © 2013 Carlson, O’Bryan, & Joyner 135
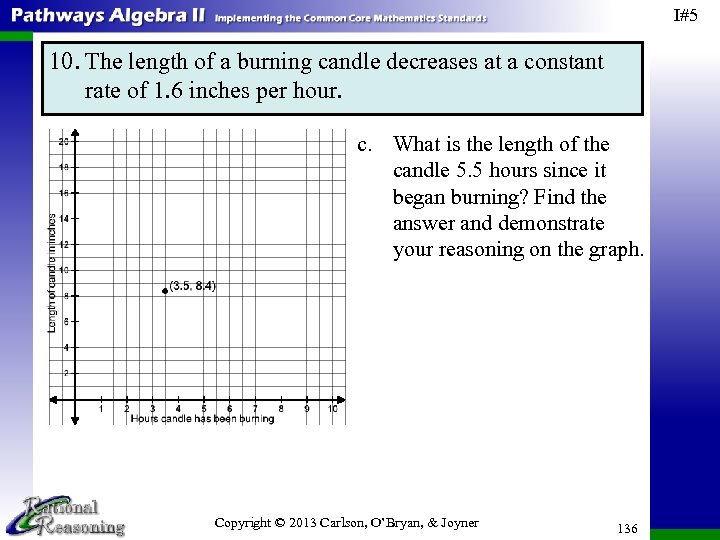 I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. c. What is the length of the candle 5. 5 hours since it began burning? Find the answer and demonstrate your reasoning on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 136
I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. c. What is the length of the candle 5. 5 hours since it began burning? Find the answer and demonstrate your reasoning on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 136
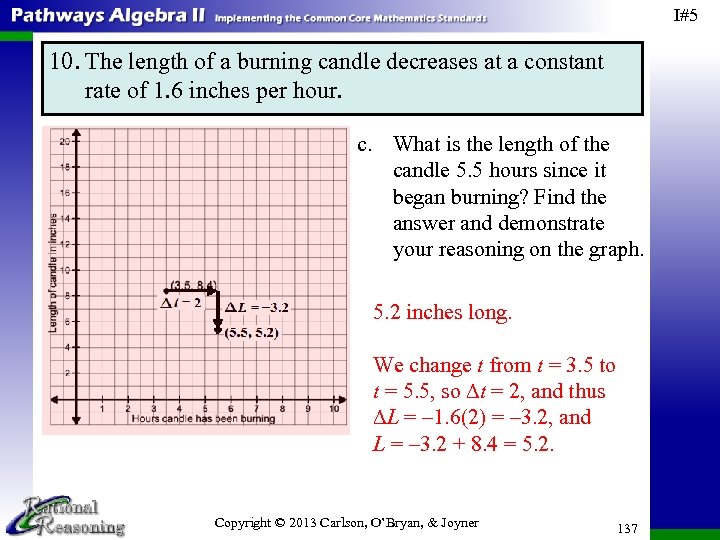 I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. c. What is the length of the candle 5. 5 hours since it began burning? Find the answer and demonstrate your reasoning on the graph. 5. 2 inches long. We change t from t = 3. 5 to t = 5. 5, so ∆t = 2, and thus ∆L = – 1. 6(2) = – 3. 2, and L = – 3. 2 + 8. 4 = 5. 2. Copyright © 2013 Carlson, O’Bryan, & Joyner 137
I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. c. What is the length of the candle 5. 5 hours since it began burning? Find the answer and demonstrate your reasoning on the graph. 5. 2 inches long. We change t from t = 3. 5 to t = 5. 5, so ∆t = 2, and thus ∆L = – 1. 6(2) = – 3. 2, and L = – 3. 2 + 8. 4 = 5. 2. Copyright © 2013 Carlson, O’Bryan, & Joyner 137
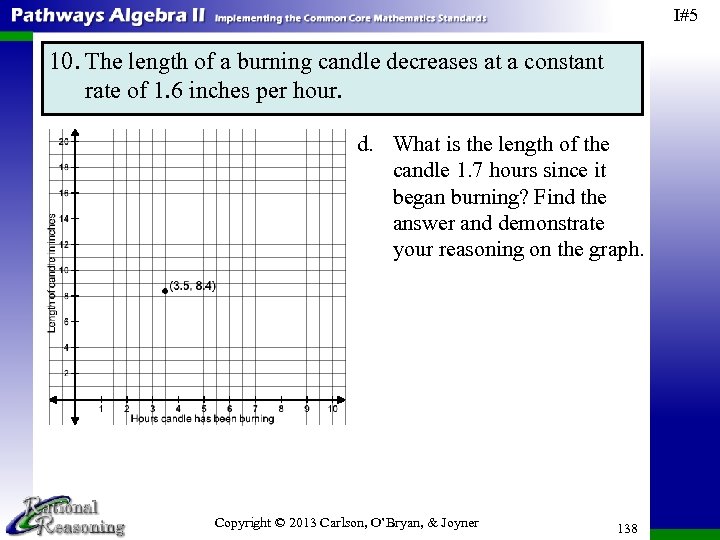 I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. d. What is the length of the candle 1. 7 hours since it began burning? Find the answer and demonstrate your reasoning on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 138
I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. d. What is the length of the candle 1. 7 hours since it began burning? Find the answer and demonstrate your reasoning on the graph. Copyright © 2013 Carlson, O’Bryan, & Joyner 138
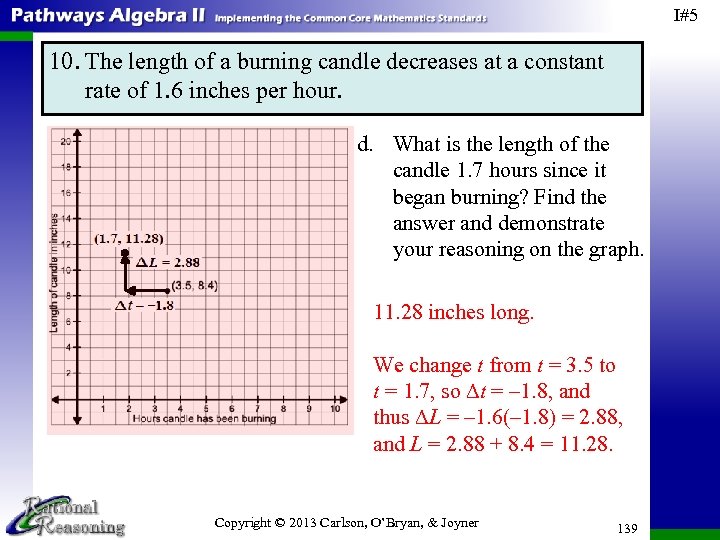 I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. d. What is the length of the candle 1. 7 hours since it began burning? Find the answer and demonstrate your reasoning on the graph. 11. 28 inches long. We change t from t = 3. 5 to t = 1. 7, so ∆t = – 1. 8, and thus ∆L = – 1. 6(– 1. 8) = 2. 88, and L = 2. 88 + 8. 4 = 11. 28. Copyright © 2013 Carlson, O’Bryan, & Joyner 139
I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. d. What is the length of the candle 1. 7 hours since it began burning? Find the answer and demonstrate your reasoning on the graph. 11. 28 inches long. We change t from t = 3. 5 to t = 1. 7, so ∆t = – 1. 8, and thus ∆L = – 1. 6(– 1. 8) = 2. 88, and L = 2. 88 + 8. 4 = 11. 28. Copyright © 2013 Carlson, O’Bryan, & Joyner 139
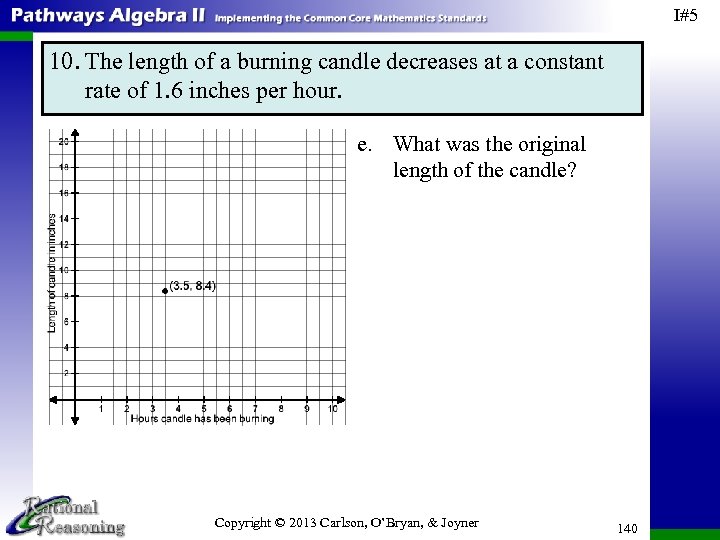 I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. e. What was the original length of the candle? Copyright © 2013 Carlson, O’Bryan, & Joyner 140
I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. e. What was the original length of the candle? Copyright © 2013 Carlson, O’Bryan, & Joyner 140
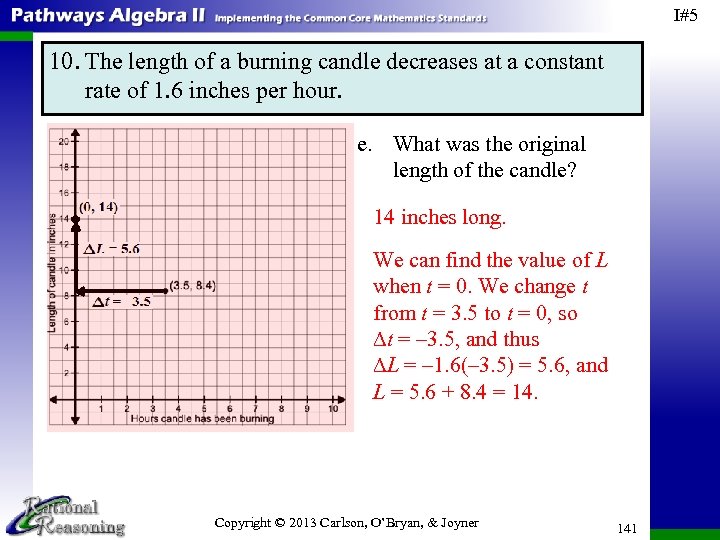 I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. e. What was the original length of the candle? 14 inches long. We can find the value of L when t = 0. We change t from t = 3. 5 to t = 0, so ∆t = – 3. 5, and thus ∆L = – 1. 6(– 3. 5) = 5. 6, and L = 5. 6 + 8. 4 = 14. Copyright © 2013 Carlson, O’Bryan, & Joyner 141
I#5 10. The length of a burning candle decreases at a constant rate of 1. 6 inches per hour. e. What was the original length of the candle? 14 inches long. We can find the value of L when t = 0. We change t from t = 3. 5 to t = 0, so ∆t = – 3. 5, and thus ∆L = – 1. 6(– 3. 5) = 5. 6, and L = 5. 6 + 8. 4 = 14. Copyright © 2013 Carlson, O’Bryan, & Joyner 141


