Modulated Unit Norm Tight Frames for Compressed Sensing

Modulated Unit Norm Tight Frames for Compressed Sensing Peng Zhang 1, Lu Gan 2, Sumei Sun 3 and Cong Ling 1 1 Department of Electrical and Electronic Engineering, Imperial College London 2 College of Engineering, Design and Physics Sciences Brunel University, United Kingdom 3 Institute for Infocomm Research, A*STAR, Singapore

Outline n Background n n n Proposed system n n n Performance bounds; Connection with existing systems; Applications in convolutional compressed sensing n n n Basics of compressed sensing; Structured random operators for compressed sensing; Compressive imaging; Sparse channel estimation in OFDM; Conclusions

Principles of Compressed Sensing (CS) n Sampling: linear, non-adaptive random projections [Candes-Romberg-Tao-2006]: y = x n n Sparsity: x has a sparse representation under a certain transform (DCT, wavelet); n n x: N× 1 signal vector; y: M× 1 sampling vector (M << N); : M×N measurement matrix; f = x can be well approximated with only K (K < M) non-zero coefficients; Reconstruction: nonlinear optimization; n n l 1 optimization; Iterative-based methods: OMP, subspace pursuit (SP) etc. ;

Principles of Compressed Sensing (CS) Restricted isometry property (RIP) [Candes-Romberg-Tao-2006]: An M×N matrix A= is said to satisfy the RIP with Parameters (K, ) if where represents the set of all length-N vectors with K non-zero coefficients.

Fully random sampling operators n : full random matrix with independent sub. Gaussian elements n n i, j follows the Gaussian or Bernoulli distributions; Optimal bound: Universal: applicable for any Limitations: n n n High computational cost in matrix multiplication; Huge buffer requirement; Difficult or even impossible to implement;

A wish-list for the sampling operator

Randomly subsampled orthonormal system n [Candes et al. -2006] S: Randomly sampling operator (choose M samples uniform at random): Q: N N Bounded unitary matrix with Example of Q: DCT, DFT, Walsh-Hadamard matrices 7

Structurally random matrices Do and Gan et al. 2008 [ICASSP], 2012 [TSP] n Random Sampling (choose M out of N) Fast transform FFT, WHT, DCT Random Sign Flipping ± 1 = ± 1 S Fast implementation ± 1 F D Universal Random sampling could be difficult! 8

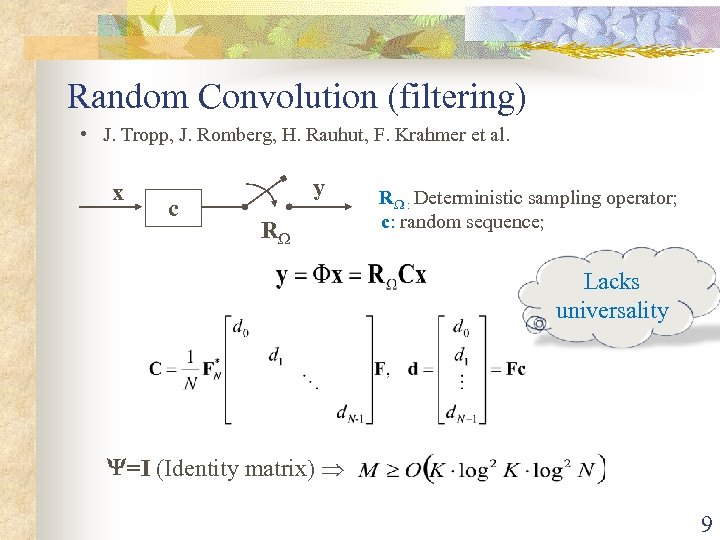Random Convolution (filtering) • J. Tropp, J. Romberg, H. Rauhut, F. Krahmer et al. x c y R R : Deterministic sampling operator; c: random sequence; Lacks universality =I (Identity matrix) 9

Outline n Background n n n Proposed system n n n Performance bounds; Connection with existing systems; Examples of potential applications n n n Basics of compressed sensing; Structured random operators for compressed sensing; Compressive imaging; Sparse channel estimation in OFDM; Conclusions

Unit-norm tight frame An M×N matrix U corresponds to a unit norm tight frame if n n Each column vector has a unit norm: The rows of form an orthonormal family;

Examples of unit norm tight frame n Partial FFT or WHT: U=R F or U=R W n Partial summation operator; U= n Cascading of identity or Fourier matrices; U=[I I … I] or U=[F F … F]

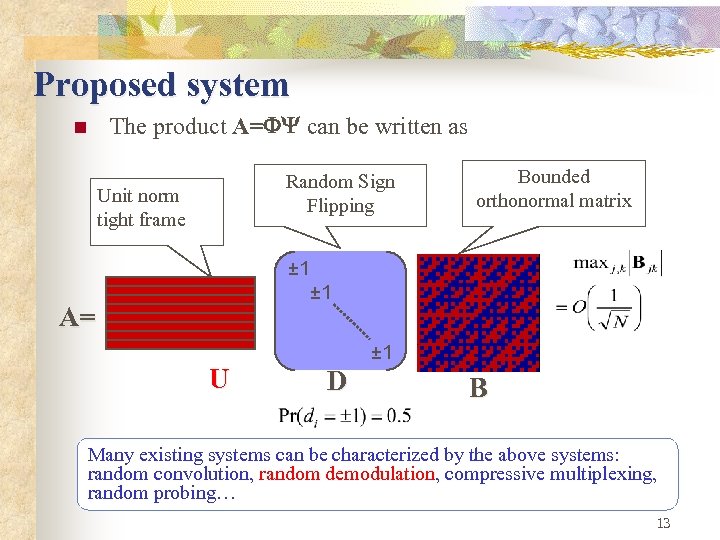Proposed system The product A= can be written as n Random Sign Flipping Unit norm tight frame Bounded orthonormal matrix ± 1 A= ± 1 U D B Many existing systems can be characterized by the above systems: random convolution, random demodulation, compressive multiplexing, random probing… 13

Performance bound n Main tools in the proof n n Suprema of chaos processes [Krahmer et al. - 2014] Variations and extensions n n The diagonal matrix D could be constructed from any sub-Gaussian variables; B could be a near-orthogonal (rectangular) matrix;

Example: Random demodulation [Tropp et al. -2010] 15

Random demodulation Sampling operator: =UD, U= Sparsifying transform : FFT matrix with column permutation Previous work [Tropp et al. 2010]: M≥ O(K log 6 N) Our bound: M ≥ O(K log 2 N)

Outline n Background n n n Proposed system n n n Performance bounds; Connection with existing systems; Applications in convolutional compressed sensing n n n Basics of compressed sensing; Structured random operators for compressed sensing; Compressive imaging; Sparse channel estimation in OFDM; Conclusions

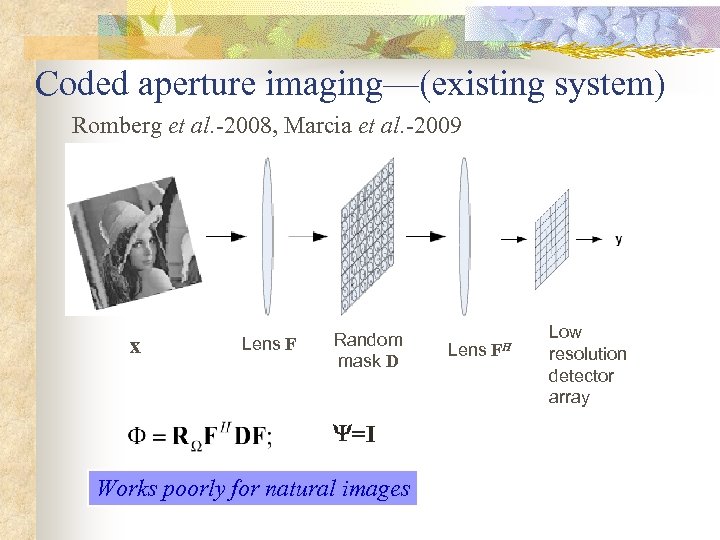Coded aperture imaging—(existing system) Romberg et al. -2008, Marcia et al. -2009 x Lens F Random mask D =I Works poorly for natural images Lens FH Low resolution detector array

Coded aperture imaging—(existing system) ü Spatially sparse, =I Fails for this one (spectrally sparse)

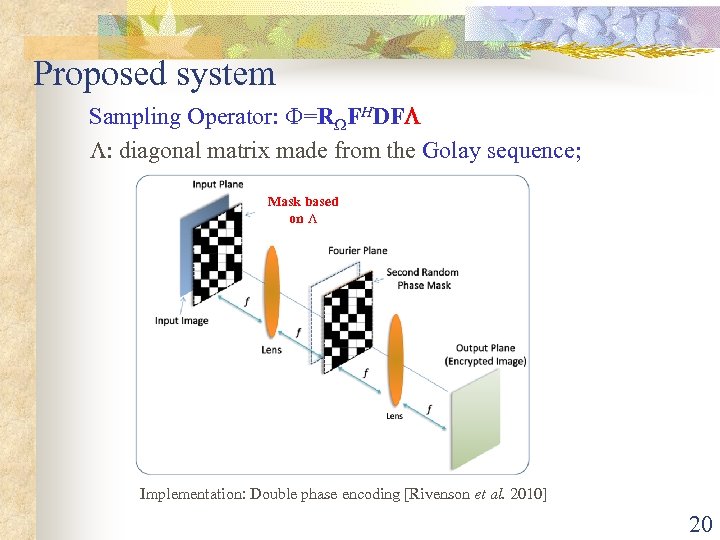Proposed system Sampling Operator: =R FHDF : diagonal matrix made from the Golay sequence; Mask based on Implementation: Double phase encoding [Rivenson et al. 2010] 20

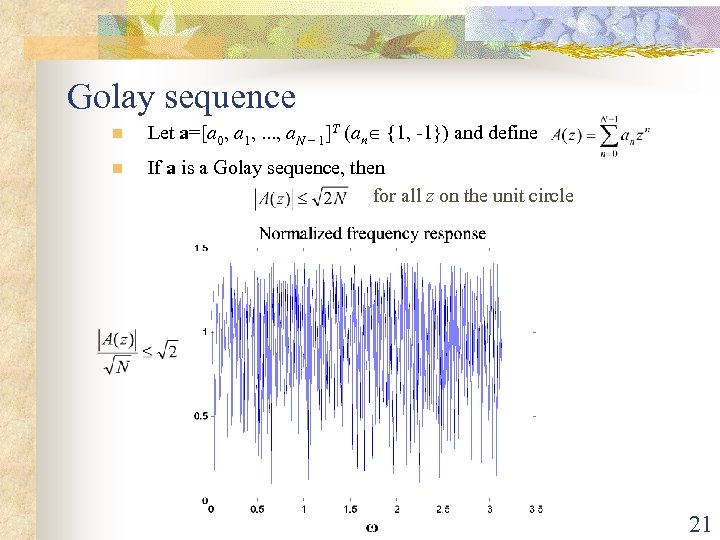Golay sequence n Let a=[a 0, a 1, . . . , a. N − 1]T (an {1, -1}) and define n If a is a Golay sequence, then for all z on the unit circle 21

Proposed system Sampling Operator: =R FHDF : diagonal matrix made from the Golay sequence; U=R FH B=F Sparsifying transform : Haar Wavelet, Fourier, (Block) DCT (popular for natural images) 22

Simulation results: Compressive imaging n Experimental setup n n n Test images: 256 Lena and Hall; Reconstruction: re-weighted BPDN [Carrillo et al. 2013] Sampling ratio M/N=0. 25

Simulation Results: Convolutional CS (a) (b) Reconstructed images of Lena. (a) Results from conventional compressive coded aperture imaging, SNR=11. 02 d. B; (b) Our proposed algorithm, SNR=29. 56 d. B;

Simulation Results (a) (b) Reconstructed images of Hall. (a) Results from conventional compressive coded aperture imaging, SNR=9. 21 d. B; (b) Our proposed system, SNR=24. 62 d. B;

Outline n Background n n n Proposed system n n n Performance bounds; Connection with existing systems; Applications in convolutional compressed sensing n n n Basics of compressed sensing; Structured random operators for compressed sensing; Compressive imaging; Sparse channel estimation in OFDM; Conclusions

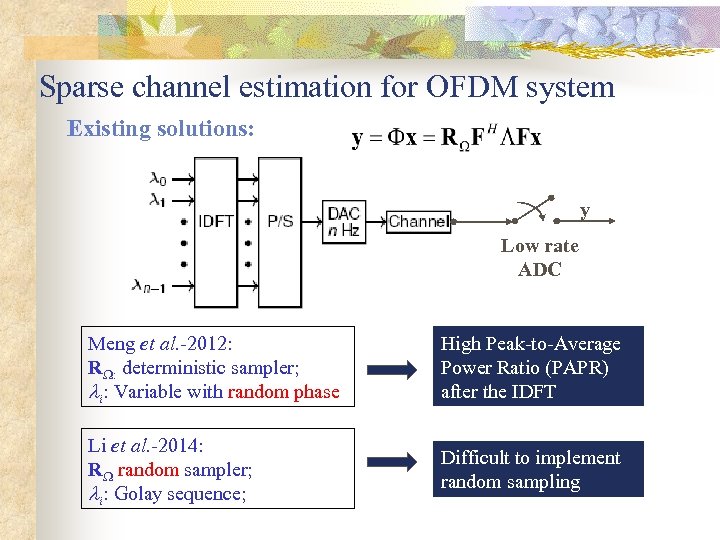Sparse channel estimation for OFDM system Existing solutions: y Low rate ADC Meng et al. -2012: R : deterministic sampler; i: Variable with random phase High Peak-to-Average Power Ratio (PAPR) after the IDFT Li et al. -2014: R random sampler; i: Golay sequence; Difficult to implement random sampling

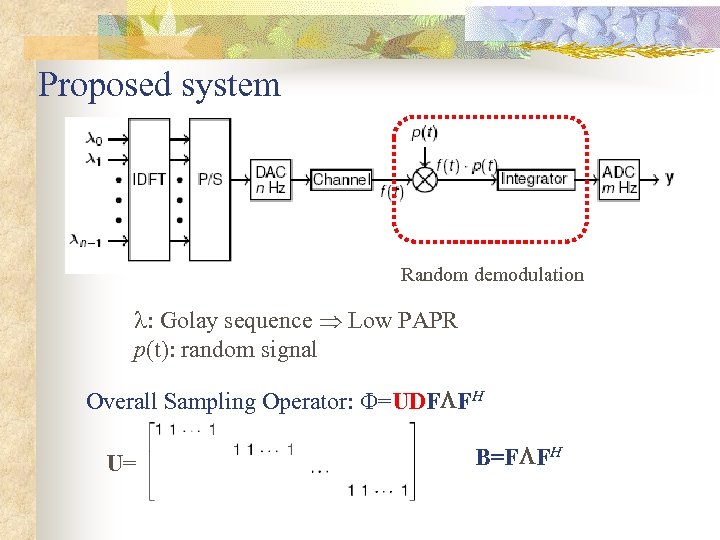Proposed system Random demodulation : Golay sequence Low PAPR p(t): random signal Overall Sampling Operator: =UDF FH U= B=F FH

Experimental setup (OFDM) n n N=1024, M=64; Channel model n ATTC (Advanced Television Technology Center) and the Grande Alliance DTV laboratory ensemble E model. n Channel impulse response n Input signal to noise ratio (SNR): 0 d. B to 30 d. B Reconstruction: subspace pursuit (Dai et al. -2009) n

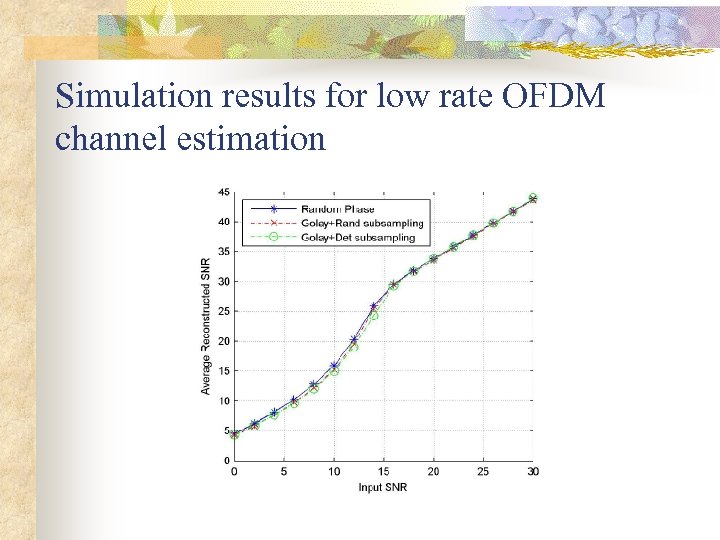Simulation results for low rate OFDM channel estimation

Conclusions n Proposed framework A= =UDB n n n U: unit norm tight frame, D: random diagonal matrix, B: bounded orthogonal matrix; M ≥ O(K log 2 N) Improved performance bound for existing system n Random demodulation, compressive multiplexing, random probing etc. n Novel compressive sensing framework n Compressive imaging; n Sparse channel estimation for OFDM systems;