MODULAR SYSTEMS COMBINATORIAL OPTIMIZATION based on course

MODULAR SYSTEMS & COMBINATORIAL OPTIMIZATION (based on course “System design”, 2004… 2008, MIPT) Mark Sh. Levin Inst. for Inform. Transmission Problems, Russian Acad. of Sci. Email: mslevin@acm. org Http: //www. mslevin. iitp. ru/ PLAN: 1. Preliminaries (about me, about you) 2. Modularity (applications, basic technological problem) 3. Decision cycle (problem, model, algorithm, computing, decisions) 4. Combinatorial optimization problems 5. Four-layer framework (basic combinatorial problems/models, composite models, framework of problems, applied layer) 6. Composite problems – research projects 7. Conclusion (about novelty) Dept. ‘Technology for Complex System Modeling”, Division of Applied Mathematics&Informatics, HSE, Moscow, Russia, Dec. 19, 2012

PRELIMINARIES GOALS: 1. Extending your thinking 2. Possible joint research 3. Usage of my materials About me: A. Education: (a) Radio Engineering (MTUSI, 1970) (b) Mehmat (MSU, 1975) (c) Faculty of Economics (Ph. D-studies, MSU)(1981) (d) Ph. D-engineering & CS (RAS) B. Works: (i) system design, (ii) software engineering: information software packages, (iii)management systems (iv)decision making + COMBINATORIAL OPTIMIZATION Applications: (a) special systems, (b) governmental organizations (c) manufacturing, (d) geology, (e) house-building, (f) machine-building, (g) communication C. Recent teaching: Moscow Univs. ; MIPT (2004. . 2008): “System Design” About you: 1. Your future objectives (i) Work in bank, consulting company, etc. (ii) Establishing new company (Google, Microsoft, Facebook, etc. ) (iii) Academic research & educational work: *BS level: 1. . . 3 conf. papers *MS level: 1… 3 conf. papers, 1… 3 journal articles (Wo. S) Ph. D level: 3… 5 conf. papers, 3… 5 journal articles (Wo. S) Assistant Prof. level: 8… 15 conf. papers, 5… 7, journal articles (Wo. S) Associate Prof. level: 30 journal articles (Wo. S), 30 conf. papers Full Prof. level: 60 journal articles (Wo. S), 60 conf. papers

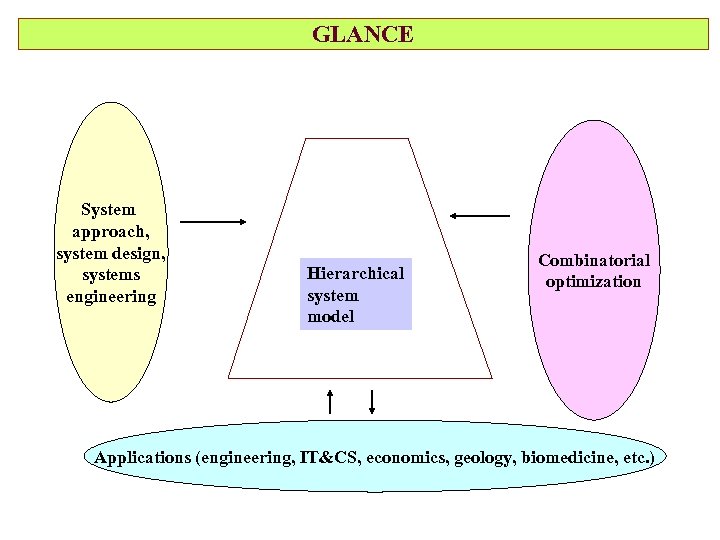
GLANCE System approach, system design, systems engineering Hierarchical system model Combinatorial optimization Applications (engineering, IT&CS, economics, geology, biomedicine, etc. )

MODULARITY APPLICATIONS: (1)House-building (2)Computers (3)Machine-building (4)Bioinformatics (5)Software, (6)Combinatorial chemistry, ETC BASIC EXAMPLE: linguistics (NB!) BASIC SYSTEM PROBLEMS: 1. System model (system hierarchy, architecture) 2. System design (system configuration) 3. System improvement/upgrade (adaptation, modification, reconfiguration) 4. Multi-stage system design (design of system trajectory) 5. Combinatorial system evolution (combinatorial modeling) 6. System forecasting SYSTEM: 1. Basic (e. g. , physical) system (e. g. , computer, machine/car, house, communication system, software, algorithm system, personnel) 2. Plan: medical treatment, plan of system improvement, economical plan, rules 3. Requirements (system of requirements) 4. Standard (standard as system, system of standard)

COMBINATORIAL OPTIMIZATION PROBLEMS COMBINATORIAL PROBLEMS (basic problems): There is a set of elements. Find: Basic Problem 1. Ordering of elements Basic Problem 2. Grouping of elements Basic Problem 3. Assignment of elements to certain “places” PROBLEMS: 1. Ordering/scheduling 2. Ranking 3. Knapsack problem 4. Multiple choice problem 5. Assignemnt/allocation/location problems (including marriage problem) 6. Clustering (grouping) 7. TSP 8. Graph coloring 9. Covering problems 10. Spanning trees (minimum spanning tree, Steiner tree) 11. SAT etc. BASIC ISSUES: 1. Complexity (Polynomial algorithm exists or does not exist) 2. Design of algorithms: (a) enumerative methods (B-A-B, dynamic programming) (b) polynomial algorithms (c) simple (e. g. , greedy) heuristics (c) heuristics (d) approximation algorithms (e) genetic algorithms (evolutionary optimization)

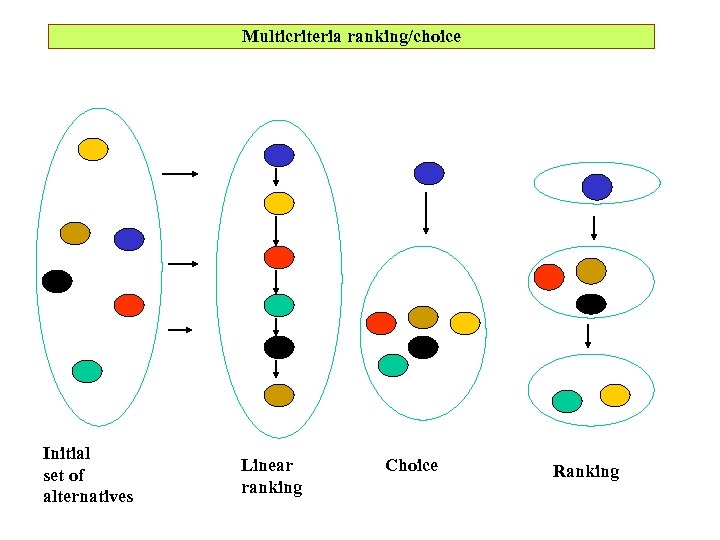
Multicriteria ranking/choice Initial set of alternatives Linear ranking Choice Ranking

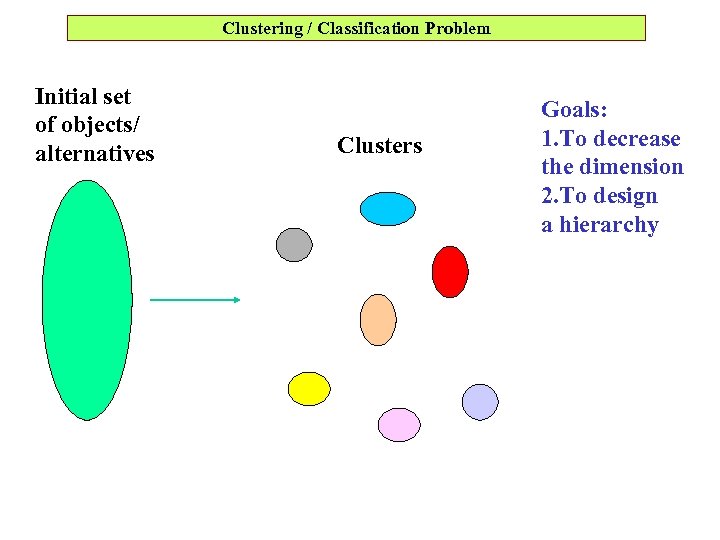
Clustering / Classification Problem Initial set of objects/ alternatives Clusters Goals: 1. To decrease the dimension 2. To design a hierarchy

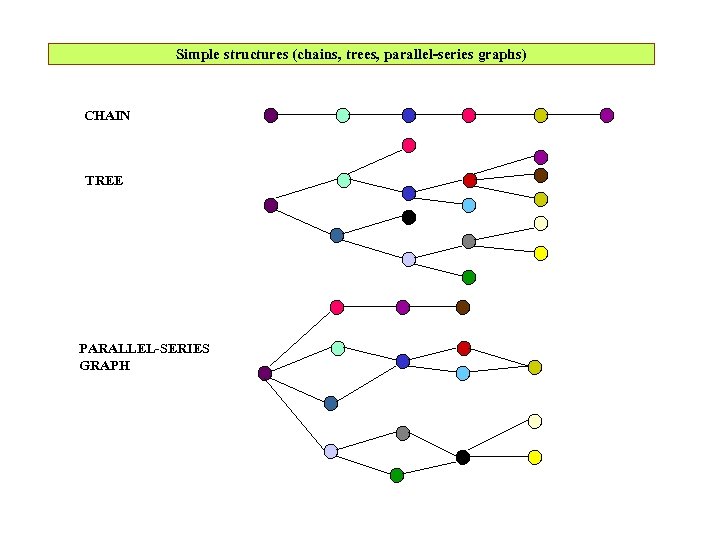
Simple structures (chains, trees, parallel-series graphs) CHAIN TREE PARALLEL-SERIES GRAPH

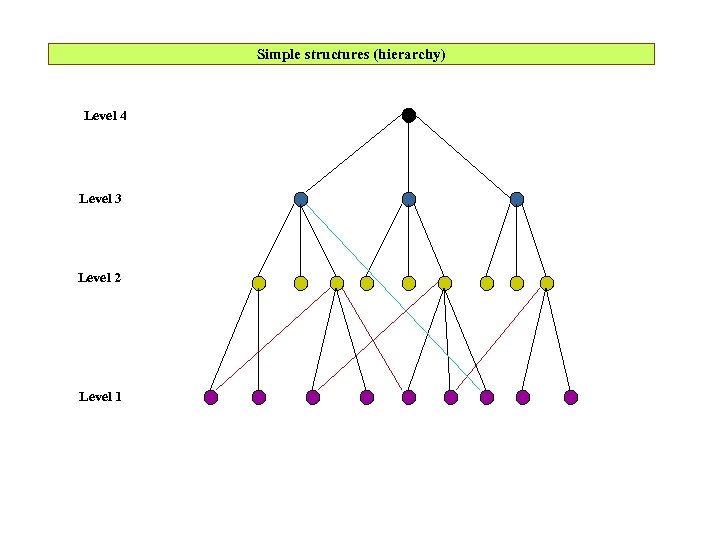
Simple structures (hierarchy) Level 4 Level 3 Level 2 Level 1

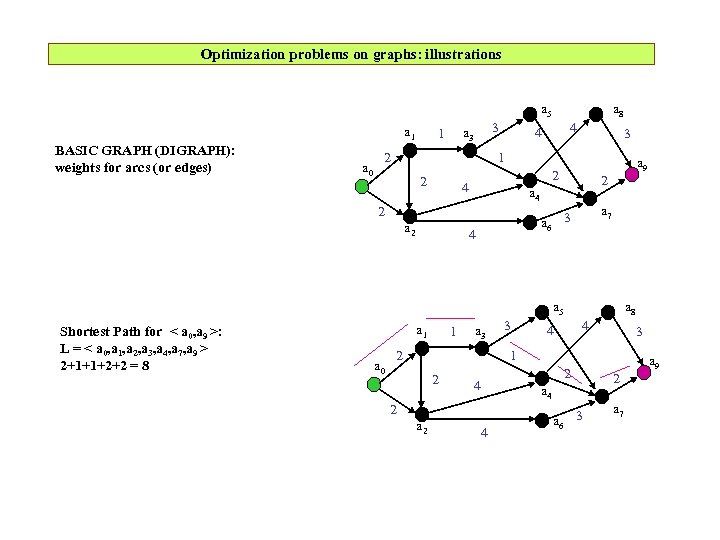
Optimization problems on graphs: illustrations a 5 a 1 BASIC GRAPH (DIGRAPH): weights for arcs (or edges) a 0 3 a 3 1 2 a 8 4 4 3 1 2 2 a 6 3 4 a 7 a 4 2 a 9 2 4 a 5 Shortest Path for < a 0, a 9 >: L = < a 0, a 1, a 2, a 3, a 4, a 7, a 9 > 2+1+1+2+2 = 8 a 1 a 0 1 a 3 2 3 a 8 4 4 3 1 2 4 2 a 6 3 a 7 a 4 2 a 9 2 4

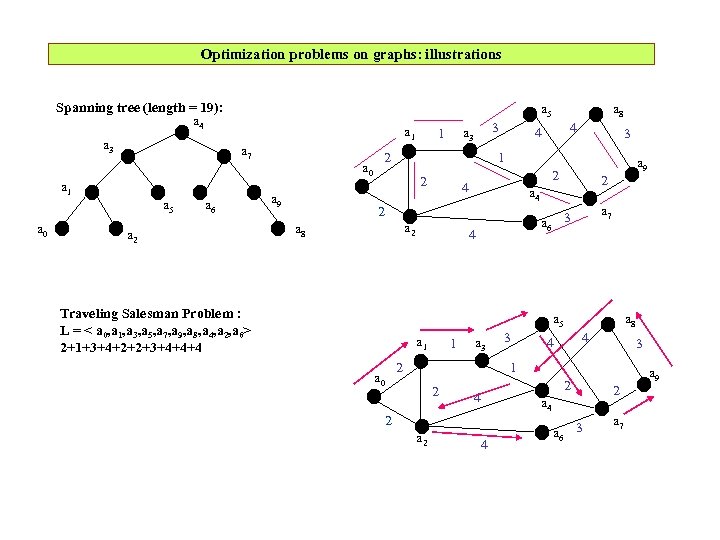
Optimization problems on graphs: illustrations Spanning tree (length = 19): a 4 a 3 a 5 a 1 a 7 a 1 a 5 a 0 a 6 a 2 a 0 a 9 3 a 3 1 2 a 8 4 4 3 1 2 a 2 Traveling Salesman Problem : L = < a 0, a 1, a 3, a 5, a 7, a 9, a 8, a 4, a 2, a 6> 2+1+3+4+2+2+3+4+4+4 2 a 6 3 4 a 7 a 4 2 a 8 a 9 2 4 a 5 a 1 a 0 1 a 3 2 3 a 8 4 4 3 1 2 4 2 a 6 3 a 7 a 4 2 a 9 2 4

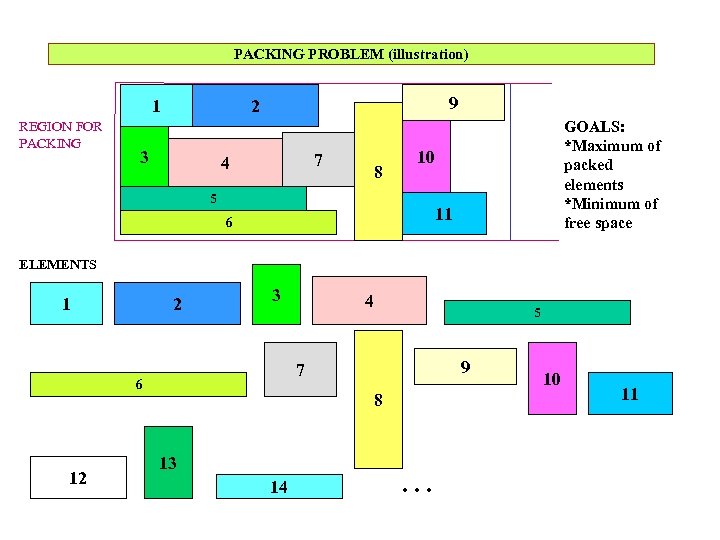
PACKING PROBLEM (illustration) 1 REGION FOR PACKING 9 2 3 7 4 8 GOALS: *Maximum of packed elements *Minimum of free space 10 5 11 6 ELEMENTS 1 2 3 5 9 7 6 12 4 8 13 14 . . . 10 11

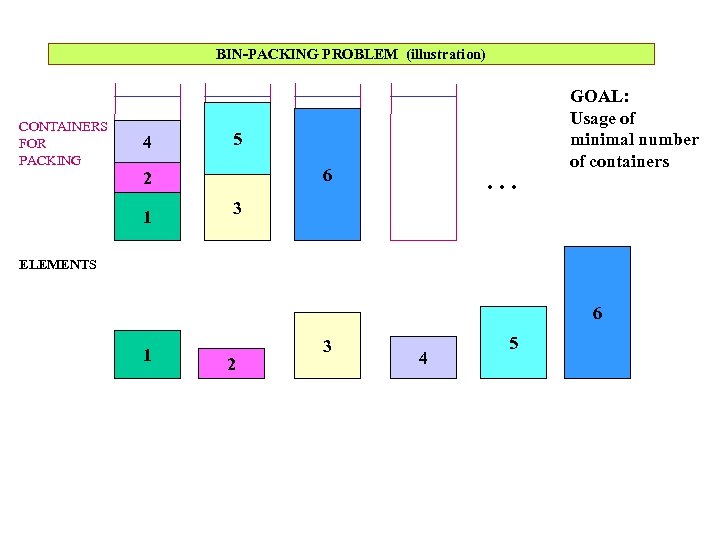
BIN-PACKING PROBLEM (illustration) CONTAINERS FOR PACKING 4 5 6 2 1 . . . GOAL: Usage of minimal number of containers 3 ELEMENTS 6 1 2 3 4 5

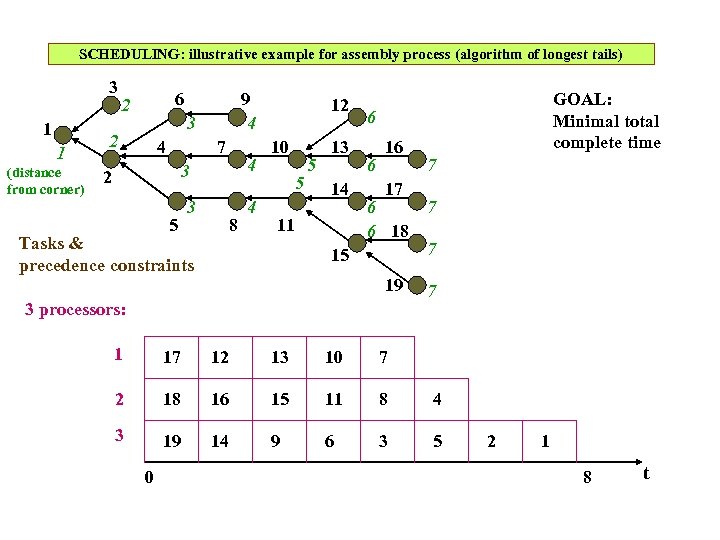
SCHEDULING: illustrative example for assembly process (algorithm of longest tails) 3 1 1 (distance from corner) 6 2 9 4 3 2 4 7 4 3 2 5 3 8 Tasks & precedence constraints 4 12 10 5 5 13 14 11 GOAL: Minimal total complete time 6 6 16 17 6 6 18 15 19 3 processors: 7 7 1 17 12 13 10 7 2 18 16 15 11 8 4 3 19 14 9 6 3 5 0 2 1 8 t

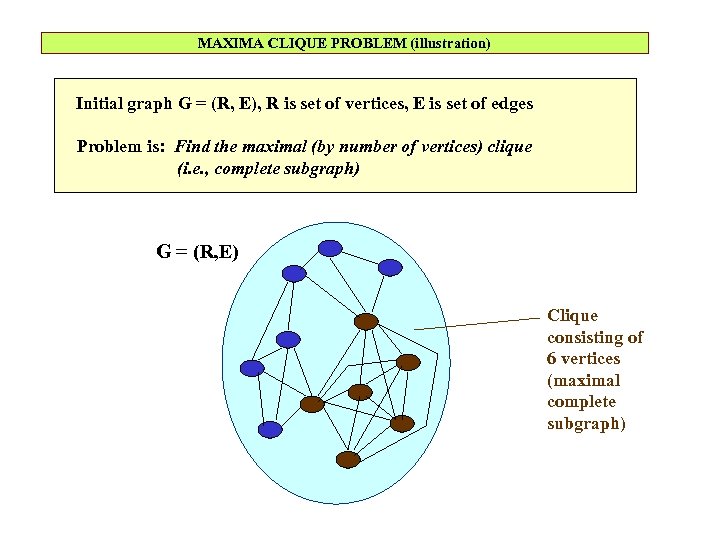
MAXIMA CLIQUE PROBLEM (illustration) Initial graph G = (R, E), R is set of vertices, E is set of edges Problem is: Find the maximal (by number of vertices) clique (i. e. , complete subgraph) G = (R, E) Clique consisting of 6 vertices (maximal complete subgraph)

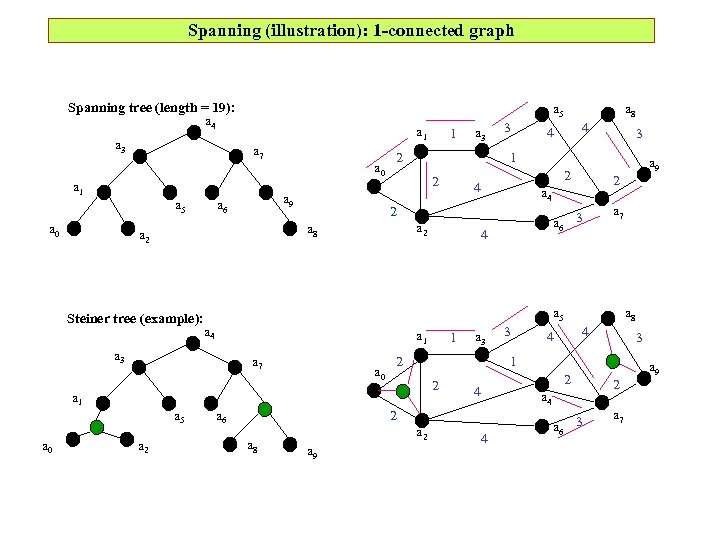
Spanning (illustration): 1 -connected graph Spanning tree (length = 19): a 4 a 3 a 5 a 1 a 7 a 1 a 5 a 0 a 9 a 6 Steiner tree (example): 3 2 2 a 6 3 4 a 2 a 9 2 a 7 a 4 2 a 4 4 a 1 a 7 a 2 4 4 1 a 0 a 6 1 a 3 2 2 a 9 4 4 3 a 9 2 4 2 a 6 3 a 7 a 4 2 a 8 3 a 8 1 a 0 3 a 5 a 3 2 a 8 a 2 1 a 8 4

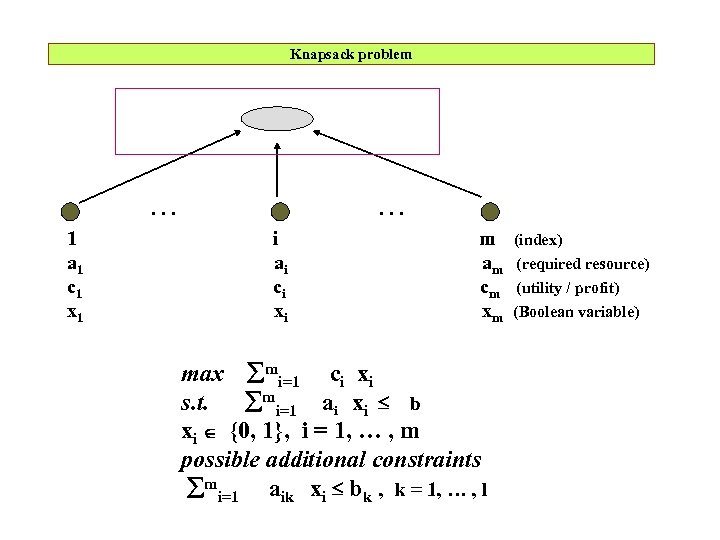
Knapsack problem . . . 1 a 1 c 1 x 1 . . . i ai ci xi m am cm xm max mi=1 ci xi s. t. mi=1 ai xi b xi {0, 1}, i = 1, … , m possible additional constraints mi=1 aik xi bk , k = 1, … , l (index) (required resource) (utility / profit) (Boolean variable)

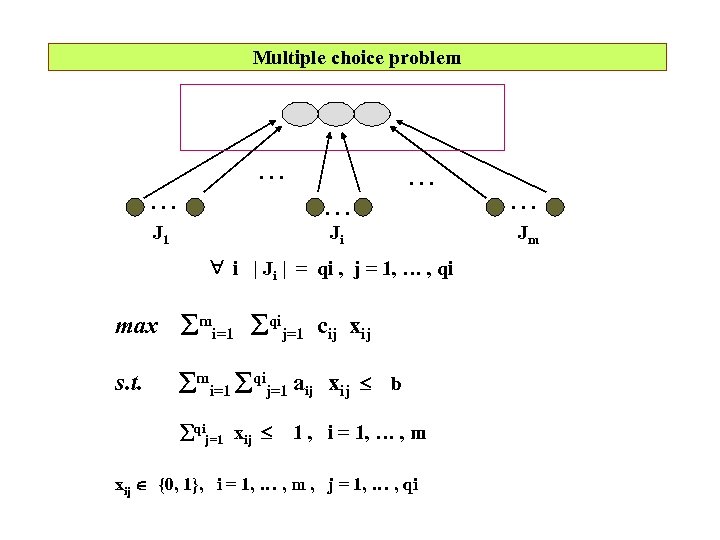
Multiple choice problem . . . J 1 . . . Ji i | Ji | = qi , j = 1, … , qi max mi=1 qij=1 cij xij s. t. mi=1 qij=1 aij xij b qij=1 xij 1 , i = 1, … , m xij {0, 1}, i = 1, … , m , j = 1, … , qi . . . Jm

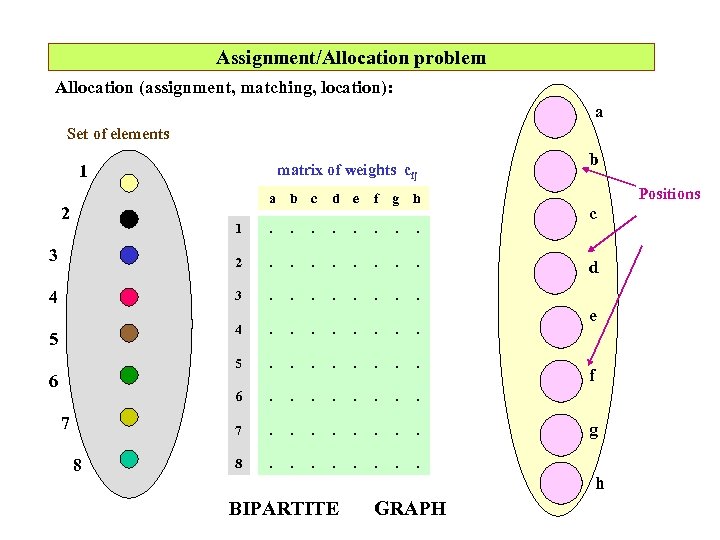
Assignment/Allocation problem Allocation (assignment, matching, location): a Set of elements matrix of weights cij 1 a b c d e f g h 1 . . . . 3 2 . . . . 4 3 . . . . 5 . . . . 6 . . . . 7 . . . . 8 . . . . Positions . 4 b . 2 5 6 7 8 c d e f g h BIPARTITE GRAPH

Assignment/allocation problem a 1 a 2 ELEMENTS b 1 b 2 b 3 a 3 POSITIONS . . . an bm FORMULATION (algebraic): Set of elements: A = { a 1 , … , ai , … , an } Set of positions: B = { b 1 , … , bj , …. bm } (now let n = m) Effectiveness of pair ai and bj is: c ( ai , bj ) xij = 1 if ai is located into position bj and 0 otherwise ( xij { 0, 1 } ) The problem is: max ni=1 nj=1 cij xij s. t. ni=1 xij = 1 nj=1 xij = 1 j i

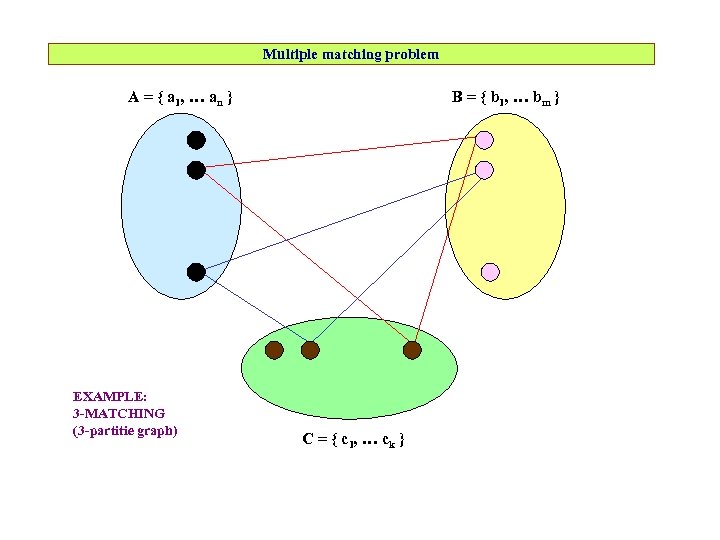
Multiple matching problem A = { a 1, … an } EXAMPLE: 3 -MATCHING (3 -partitie graph) B = { b 1, … bm } C = { c 1, … ck }

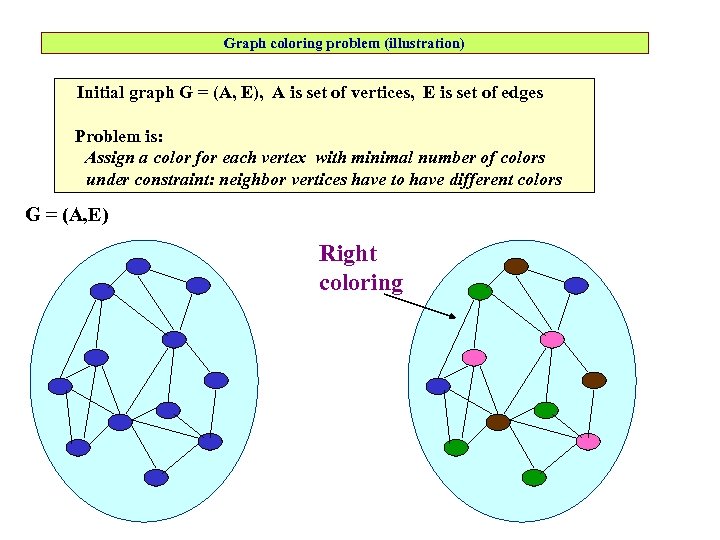
Graph coloring problem (illustration) Initial graph G = (A, E), A is set of vertices, E is set of edges Problem is: Assign a color for each vertex with minimal number of colors under constraint: neighbor vertices have to have different colors G = (A, E) Right coloring

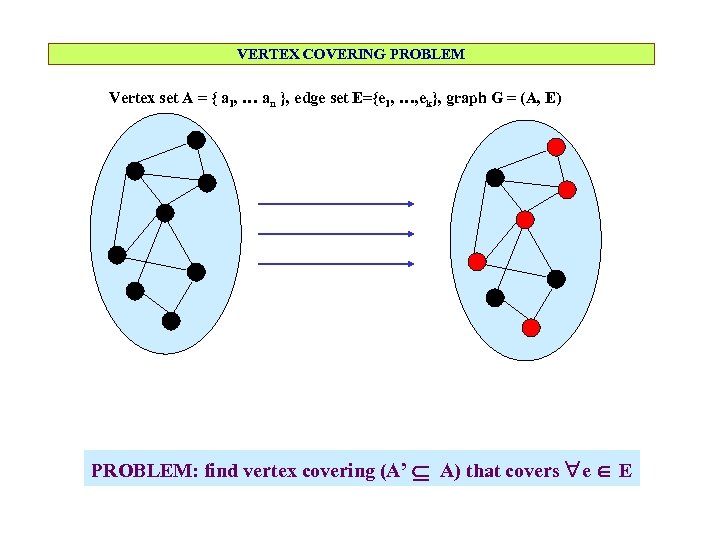
VERTEX COVERING PROBLEM Vertex set A = { a 1, … an }, edge set E={e 1, …, ek}, graph G = (A, E) PROBLEM: find vertex covering (A’ A) that covers e E

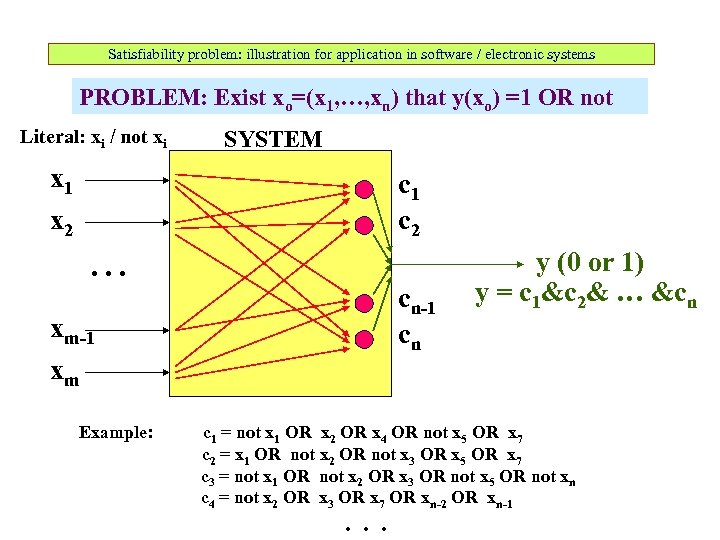
Satisfiability problem: illustration for application in software / electronic systems PROBLEM: Exist xo=(x 1, …, xn) that y(xo) =1 OR not Literal: xi / not xi SYSTEM x 1 x 2 c 1 c 2. . . cn-1 cn xm-1 xm Example: y (0 or 1) y = c 1&c 2& … &cn c 1 = not x 1 OR x 2 OR x 4 OR not x 5 OR x 7 c 2 = x 1 OR not x 2 OR not x 3 OR x 5 OR x 7 c 3 = not x 1 OR not x 2 OR x 3 OR not x 5 OR not xn c 4 = not x 2 OR x 3 OR x 7 OR xn-2 OR xn-1 . . .

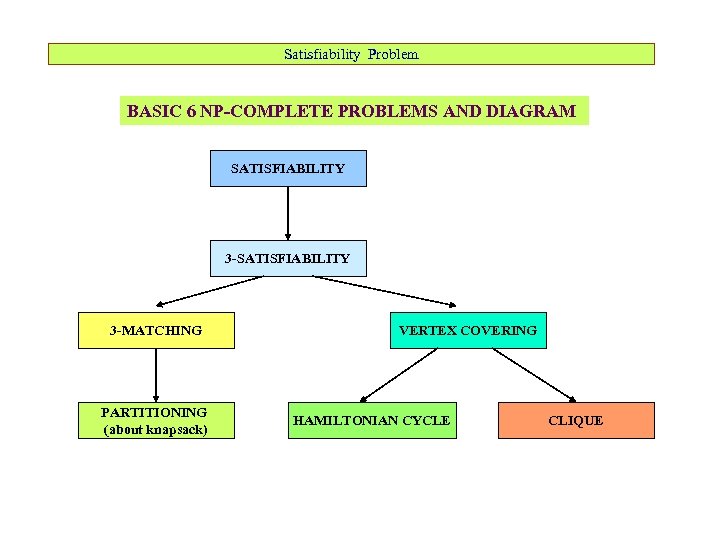
Satisfiability Problem BASIC 6 NP-COMPLETE PROBLEMS AND DIAGRAM SATISFIABILITY 3 -MATCHING PARTITIONING (about knapsack) VERTEX COVERING HAMILTONIAN CYCLE CLIQUE

Alignment (illustration) CASE OF 2 WORDS: Word 1 A B A A D D C X Word 2 A B A A B D Z X D A X C X Z Superstructure A B D C X Z

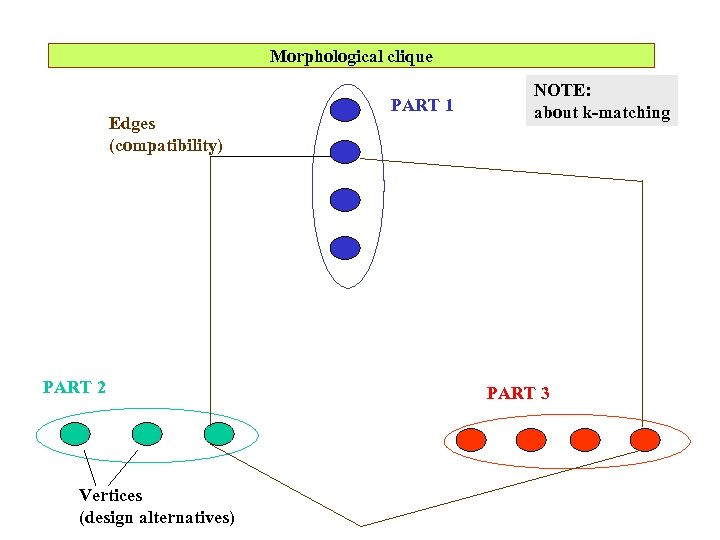
Morphological clique Edges (compatibility) PART 2 Vertices (design alternatives) PART 1 NOTE: about k-matching PART 3

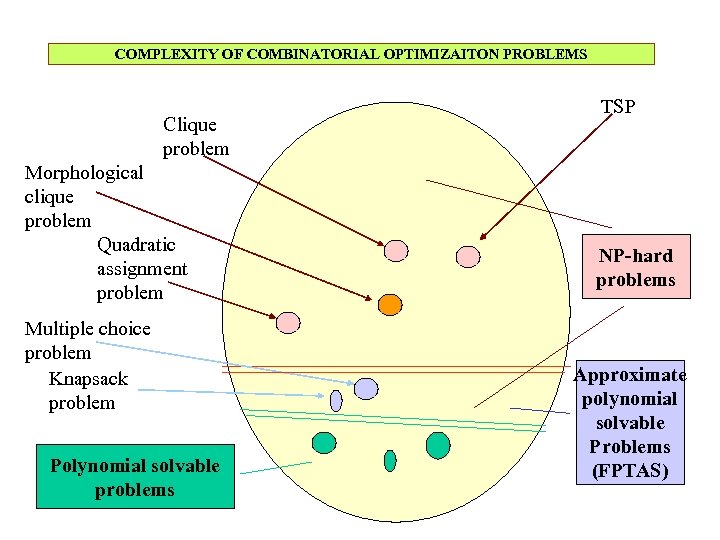
COMPLEXITY OF COMBINATORIAL OPTIMIZAITON PROBLEMS Clique problem Morphological clique problem Quadratic assignment problem Multiple choice problem Knapsack problem Polynomial solvable problems TSP NP-hard problems Approximate polynomial solvable Problems (FPTAS)

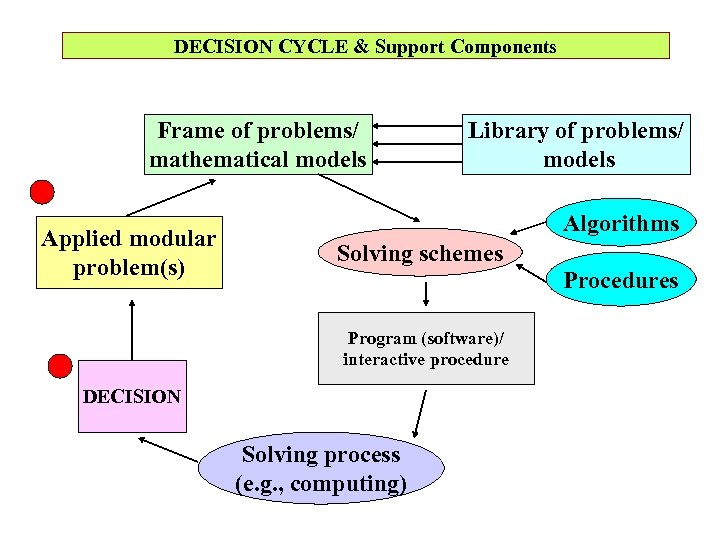
DECISION CYCLE & Support Components Frame of problems/ mathematical models Applied modular problem(s) Library of problems/ models Algorithms Solving schemes Procedures Program (software)/ interactive procedure DECISION Solving process (e. g. , computing)

Four-layer Framework Layer 4: Domain-oriented frameworks Design of Design/ Planning Improve- Evolution Modular Informamarke- planning of of ment of ETC design of tion ting of mainte- medical of requiresoftware retrieval strategy testing nance treatment network ments Layer 3: Basic (typical) solving framework Hierarchical System Four-stage morpho- upgrade/ Multistage ETC evolution/ composite design logical improveforecasting framework design ment Layer 2: Composite models/procedures Multicriteria Multi. Morpholo- Design of hierarchy Multimultiple criteria gical (clustering, criteria choice assignment/ clique multicriteria knapsack problem allocation (synthesis) spanning) ETC Layer 1: Basic problems/models Multicriteria Knapsack ranking problem Multiple Span- Steiner Shortest Cluste- Assignment/ ETC choice ning tree path ring allocation problem tree problem

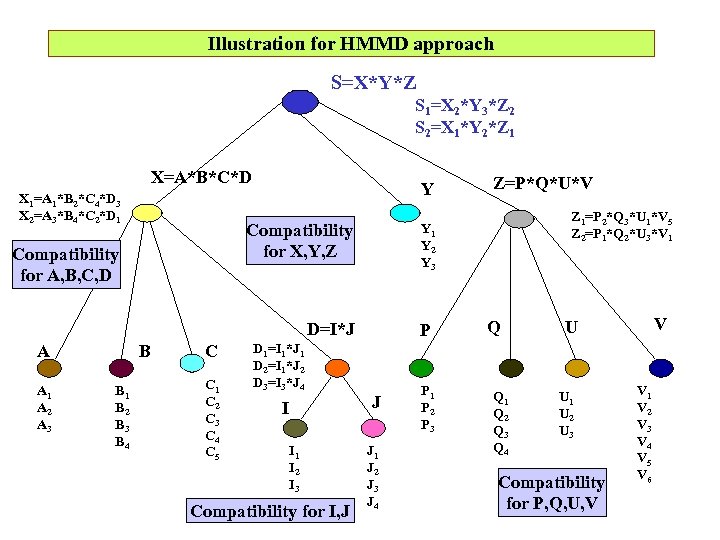
Illustration for HMMD approach S=X*Y*Z S 1=X 2*Y 3*Z 2 S 2=X 1*Y 2*Z 1 X=A*B*C*D X 1=A 1*B 2*C 4*D 3 X 2=A 3*B 4*C 2*D 1 Y Compatibility for X, Y, Z Compatibility for A, B, C, D A 1 A 2 A 3 B B 1 B 2 B 3 B 4 C C 1 C 2 C 3 C 4 C 5 D 1=I 1*J 1 D 2=I 1*J 2 D 3=I 3*J 4 I I 1 I 2 I 3 Compatibility for I, J Z 1=P 2*Q 3*U 1*V 5 Z 2=P 1*Q 2*U 3*V 1 Y 2 Y 3 D=I*J A Z=P*Q*U*V P J J 1 J 2 J 3 J 4 P 1 P 2 P 3 Q Q 1 Q 2 Q 3 Q 4 V U U 1 U 2 U 3 Compatibility for P, Q, U, V V 1 V 2 V 3 V 4 V 5 V 6

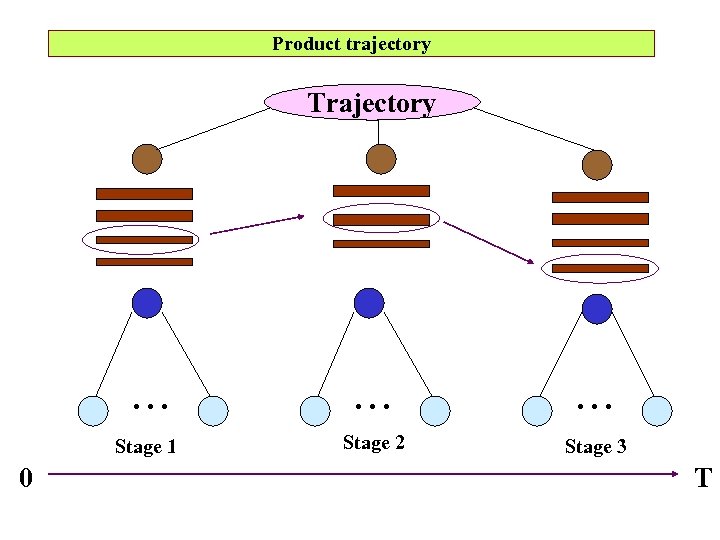
Product trajectory Trajectory . . . Stage 1 0 . . . Stage 2 Stage 3 T

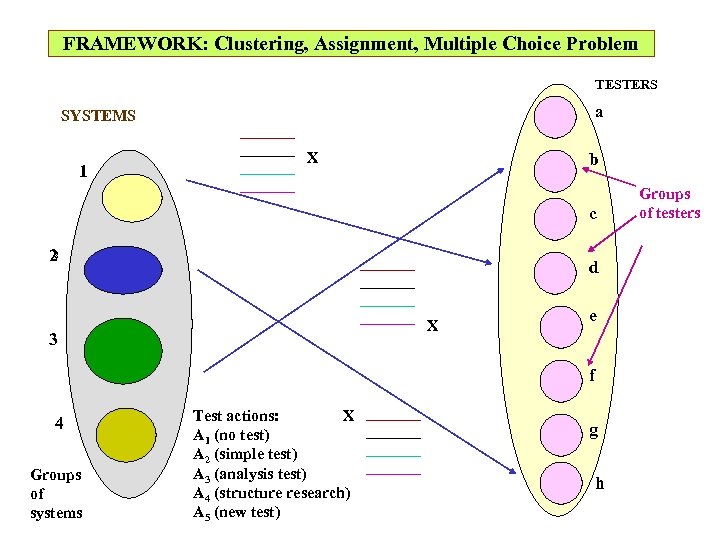
FRAMEWORK: Clustering, Assignment, Multiple Choice Problem TESTERS a SYSTEMS 1 X b c 2 2 d X 3 e f 4 Groups of systems Test actions: X A 1 (no test) A 2 (simple test) A 3 (analysis test) A 4 (structure research) A 5 (new test) g h Groups of testers

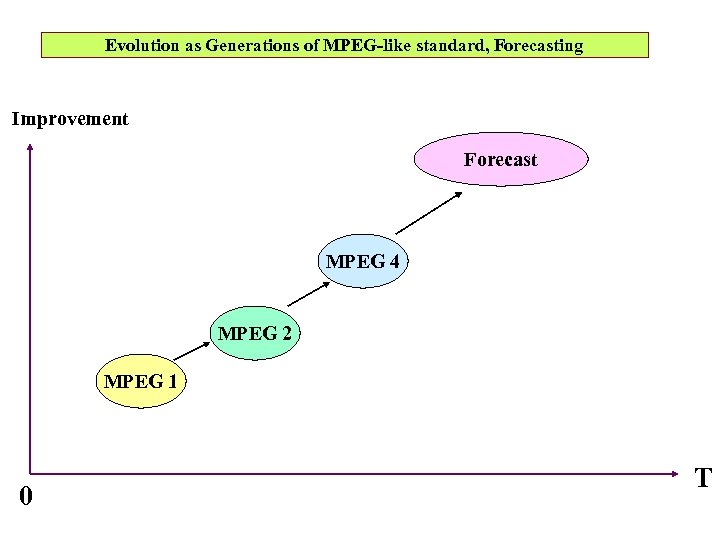
Evolution as Generations of MPEG-like standard, Forecasting Improvement Forecast MPEG 4 MPEG 2 MPEG 1 0 T

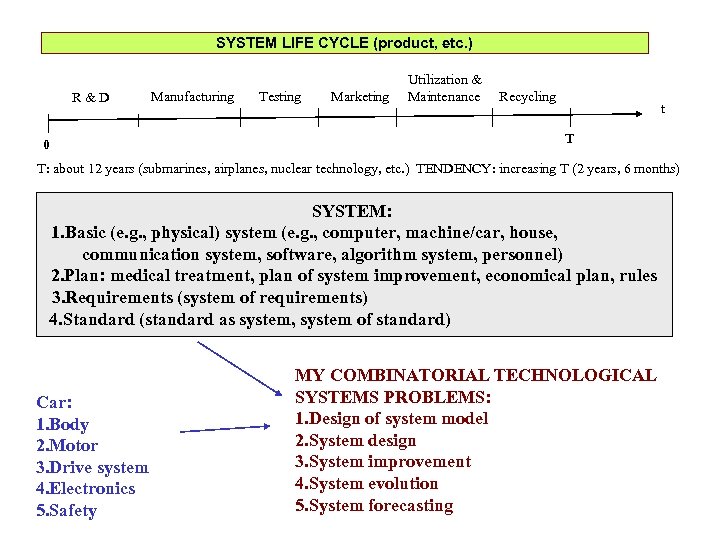
SYSTEM LIFE CYCLE (product, etc. ) R&D 0 Manufacturing Testing Marketing Utilization & Maintenance Recycling t T T: about 12 years (submarines, airplanes, nuclear technology, etc. ) TENDENCY: increasing T (2 years, 6 months) SYSTEM: 1. Basic (e. g. , physical) system (e. g. , computer, machine/car, house, communication system, software, algorithm system, personnel) 2. Plan: medical treatment, plan of system improvement, economical plan, rules 3. Requirements (system of requirements) 4. Standard (standard as system, system of standard) Car: 1. Body 2. Motor 3. Drive system 4. Electronics 5. Safety MY COMBINATORIAL TECHNOLOGICAL SYSTEMS PROBLEMS: 1. Design of system model 2. System design 3. System improvement 4. System evolution 5. System forecasting

Research Opportunity (with Novelty) Novelty: new approach at each level/for each component: 1. Applied problem (engineering, CS, economics) 2. Model/Model framework 3. Algorithm / algorithm framework 4. Software (program, program package) EXAMPLES OF STUDENT RESEARCH PROJECTS: ABOUT 30 PUBLISHED PAPERS (my site) EXAMPLES OF MY RESEARCH PROJECTS: MY PUBLISHED PAPERS (my site)

That’s All Thanks! http: //www. mslevin. iitp. ru/ Mark Sh. Levin