Modular Static Analysis with Sets and Relations for

Modular Static Analysis with Sets and Relations for Verifying Data Structure Consistency Viktor Kuncak Computer Science and Artificial Intelligence Lab MIT Joint work with: Martin Rinard Andreas Podelski Daniel Jackson Patrick Lam Thomas Wies Karen Zee Huu Hai Nguyen Peter Schmitt Suhabe Bugrara

Program analysis and verification Discover/verify properties of software systems Practical relevance: programmer productivity – performance: compiler optimizations – reliability: discovering and preventing errors – maintainability: understanding code Broader implications – automated analysis of formal artifacts (implications for XML documents, formal proofs)

Spectrum of analysis techniques Broad research area, many dimensions – bug finding versus bug prevention – control-intensive versus data-intensive systems – generic versus application-specific properties Original ideal: full program verification Reality: verify partial correctness properties – success story: type systems – active area: temporal properties (typestate) trend: towards complex properties

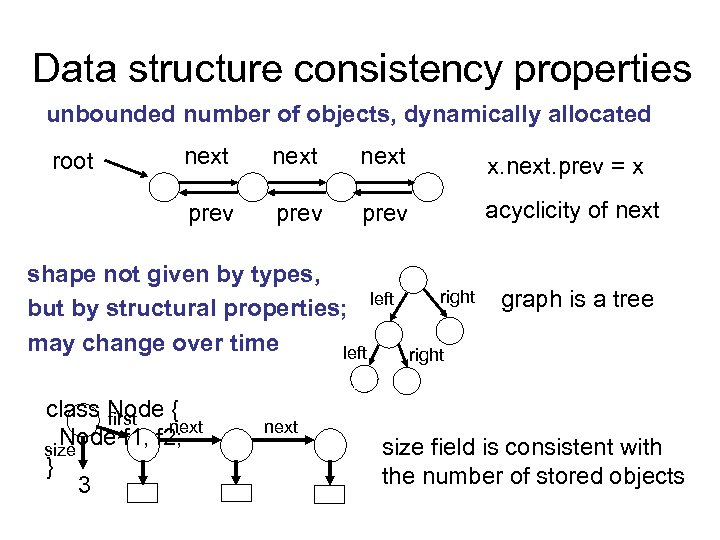Data structure consistency properties unbounded number of objects, dynamically allocated next x. next. prev = x prev root prev acyclicity of next shape not given by types, but by structural properties; left may change over time left class Node { first next Node f 1, f 2; size } 3 next right graph is a tree right size field is consistent with the number of stored objects

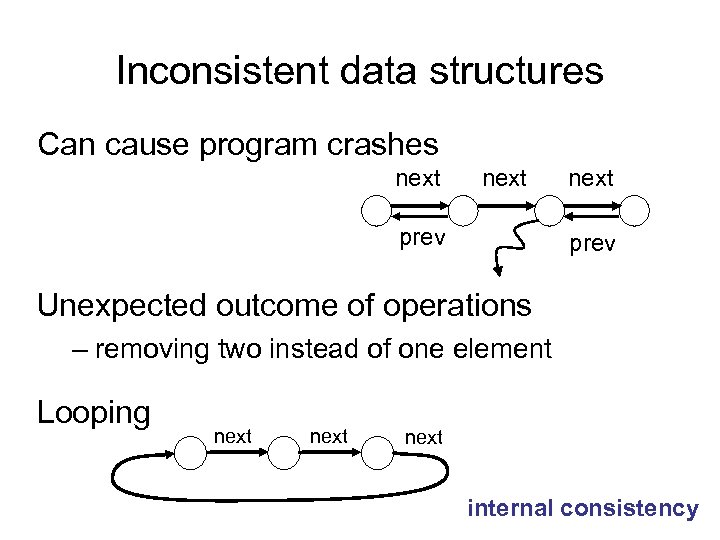Inconsistent data structures Can cause program crashes next prev Unexpected outcome of operations – removing two instead of one element Looping next internal consistency

External data structure consistency Person [0. . 1] If a person has borrowed a book, then – person is registered with library, and – book is in the catalog Two persons cannot borrow the same book borrows [0. . 4] Book A person can borrow at most 4 books at a time - correlate different data structures - global - meaningful to users of the system - capture design constraints (object models) - inconsistency can lead to policy violations relies on internal consistency to be even meaningful

Goal Prove data structure consistency – for all program executions (sound) – with high level of automation – both internal and external consistency – both implementation and use of data structures

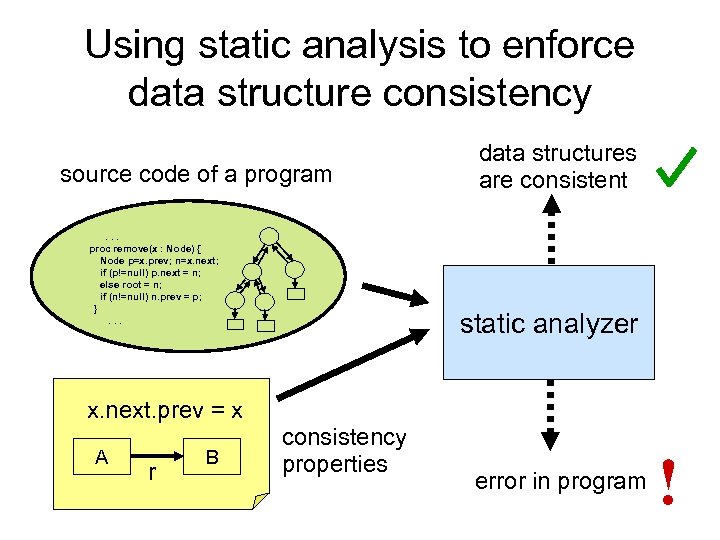Using static analysis to enforce data structure consistency source code of a program. . . proc remove(x : Node) { Node p=x. prev; n=x. next; if (p!=null) p. next = n; else root = n; if (n!=null) n. prev = p; }. . . data structures are consistent static analyzer x. next. prev = x A r B consistency properties error in program !

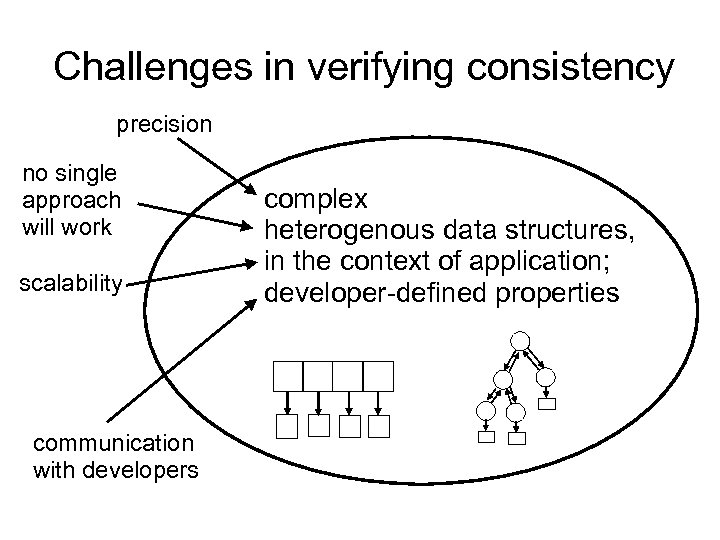Challenges in verifying consistency precision no single approach will work scalability communication with developers complex heterogenous data structures, in the context of application; developer-defined properties

Outline Goal: verify data structure consistency Our approach through an example Bohne: one of the analyses in our system Current status and ongoing work Future work

Example: Minesweeper Game (actual screenshot) Analyzed using our system (based on Java version)

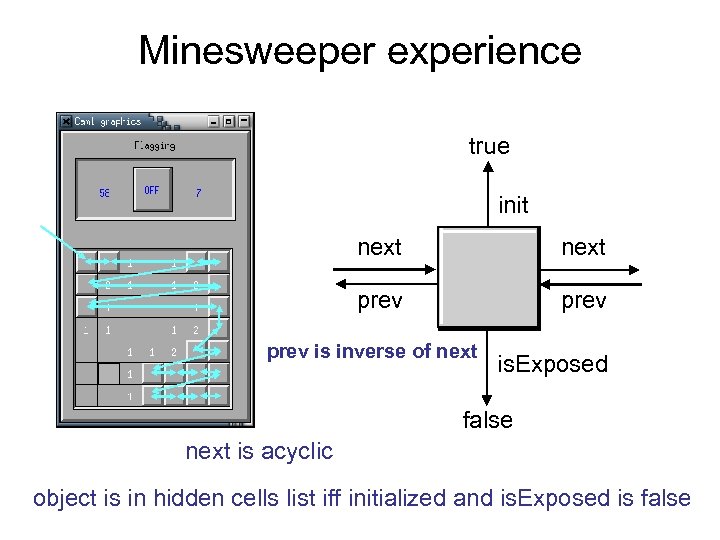
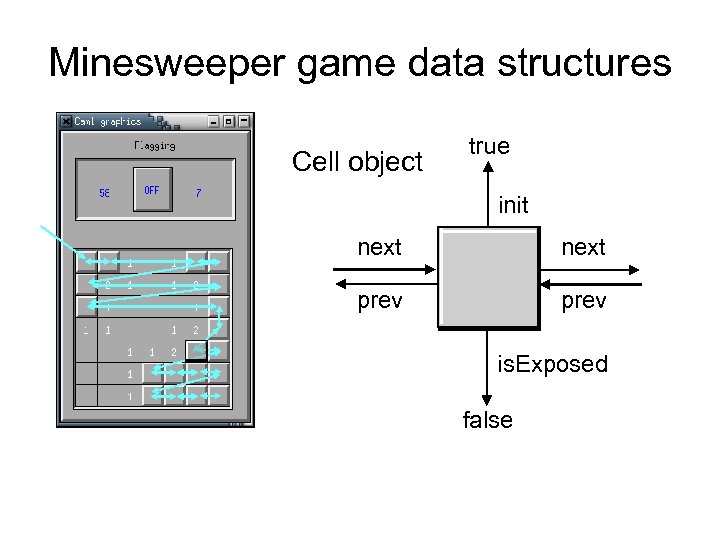Minesweeper game data structures Cell object true init next prev is. Exposed false

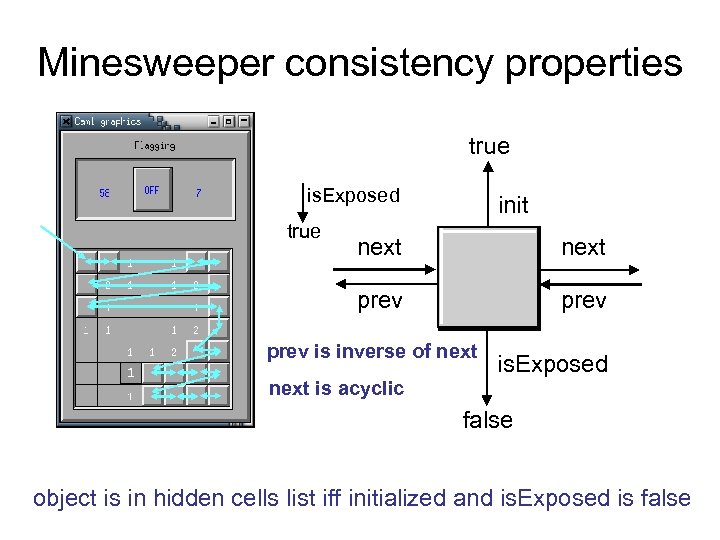Minesweeper consistency properties true is. Exposed true init next prev is inverse of next 1 next is acyclic is. Exposed false object is in hidden cells list iff initialized and is. Exposed is false

Complex consistency properties object is in hidden cells list iff its init flag is true and its is. Exposed flag is false Formalization as an invariant {x | next*(Hidden. List. Root, x) } = expression that is true whenever program reaches certain points {x | x. init & ! x. is. Exposed } Difficulties – need to track exact reachability properties – correlate linking information with stored data Need a way to deal with complexity

Towards factoring out complexity object is in hidden cells list iff its init flag is true and its is. Exposed flag is false Formalization as an invariant {x | next*(Hidden. List. Root, x) } = List. Content {x | x. init & !Unexposed. Cells x. is. Exposed } abstract reasoning in terms of sets List. Content = Unexposed. Cells = How to enable such reasoning in our program?

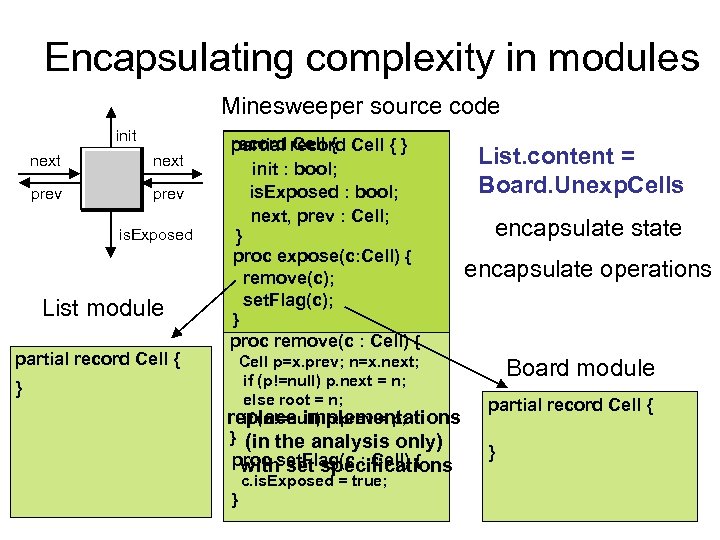Encapsulating complexity in modules Minesweeper source code init next prev is. Exposed List module partial record Cell { } record Cell { partial record Cell { } init : bool; is. Exposed : bool; next, prev : Cell; } proc expose(c: Cell) { remove(c); set. Flag(c); List. content = Board. Unexp. Cells encapsulate state encapsulate operations } proc remove(c : Cell) { Cell p=x. prev; n=x. next; if (p!=null) p. next = n; else root = n; if (n!=null) n. prev = p; replace implementations } (in the analysis only) proc set. Flag(c : Cell) { with set specifications c. is. Exposed = true; } Board module partial record Cell { }

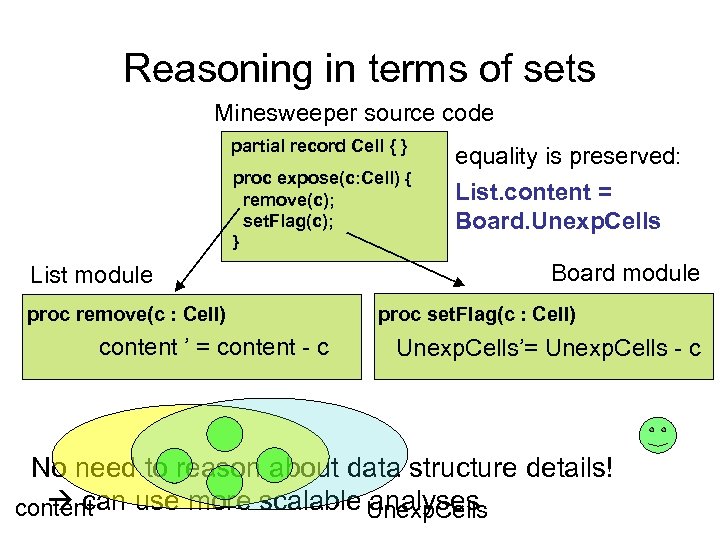Reasoning in terms of sets Minesweeper source code partial record Cell { } proc expose(c: Cell) { remove(c); set. Flag(c); } List module proc remove(c : Cell) content ’ = content - c equality is preserved: List. content = Board. Unexp. Cells Board module proc set. Flag(c : Cell) Unexp. Cells’= Unexp. Cells - c No need to reason about data structure details! can use more scalable Unexp. Cells analyses content

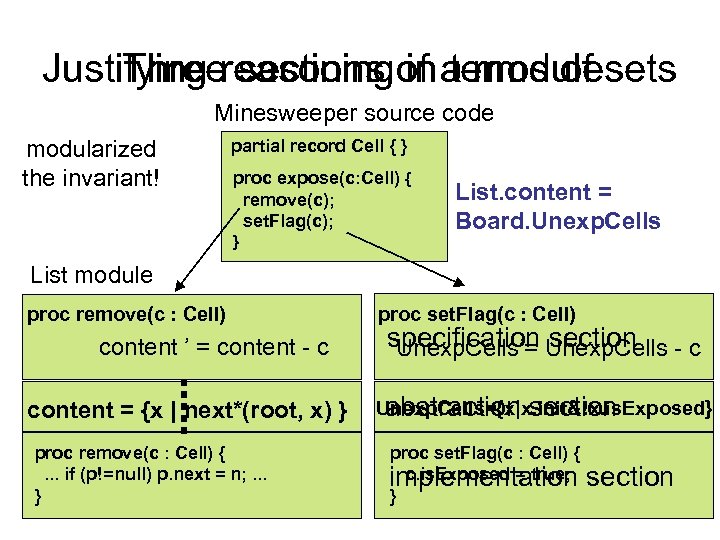Justifying reasoningof a modulesets Three sections in terms of Minesweeper source code modularized the invariant! partial record Cell { } proc expose(c: Cell) { remove(c); set. Flag(c); } List. content = Board. Unexp. Cells List module proc remove(c : Cell) content ’ = content - c content = {x | next*(root, x) } proc remove(c : Cell) {. . . if (p!=null) p. next = n; . . . } proc set. Flag(c : Cell) specification Unexp. Cells - c Unexp. Cells’= section Unexp. Cells={x|x. init&!x. is. Exposed} abstraction section proc set. Flag(c : Cell) { c. is. Exposed = true; implementation } section

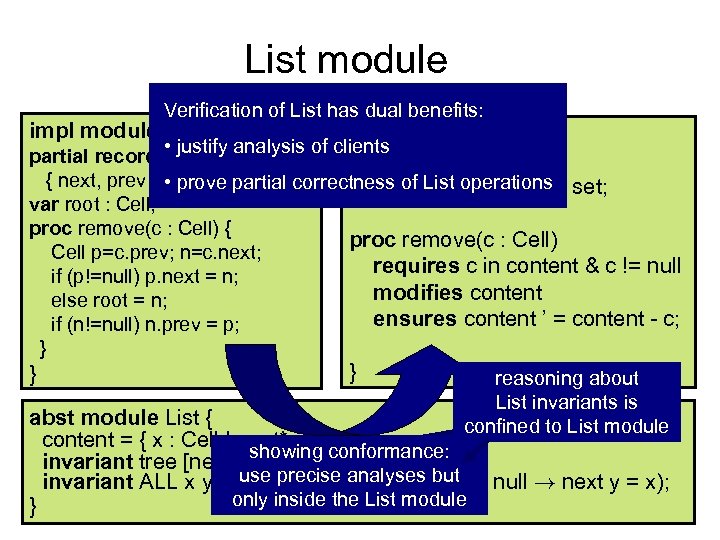List module Verification of List has dual benefits: impl module List { spec module List { • justify analysis of clients partial record Cell { next, prev : Cell; } partial correctness of List operations set; • prove specvar content : Cell var root : Cell; proc remove(c : Cell) { proc remove(c : Cell) Cell p=c. prev; n=c. next; requires c in content & c != null if (p!=null) p. next = n; modifies content else root = n; ensures content ’ = content - c; if (n!=null) n. prev = p; } } } reasoning about List invariants is abst module List { confined to List module content = { x : Cell | next* root x} ; invariant tree [next]; showing conformance: use precise (x null Æ invariant ALL x y. prev x = y !analyses buty null ! next y = x); only inside the List module }

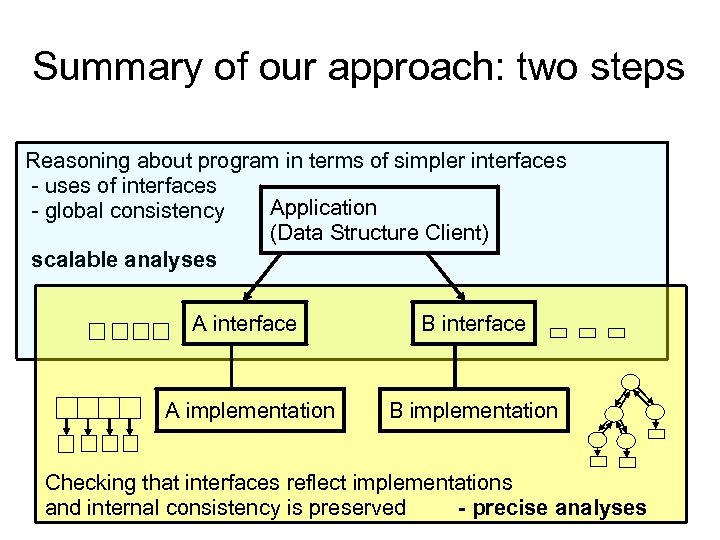Summary of our approach: two steps Reasoning about program in terms of simpler interfaces - uses of interfaces Application - global consistency (Data Structure Client) scalable analyses A interface B interface A implementation B implementation Checking that interfaces reflect implementations and internal consistency is preserved - precise analyses

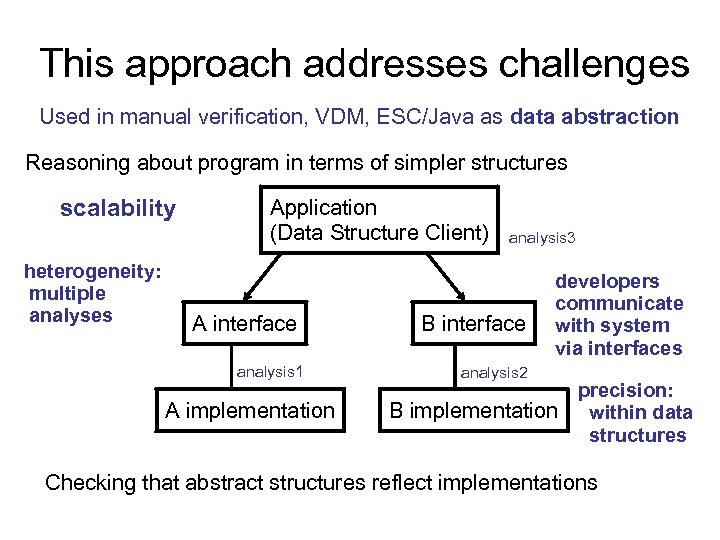This approach addresses challenges Used in manual verification, VDM, ESC/Java as data abstraction Reasoning about program in terms of simpler structures scalability heterogeneity: multiple analyses Application (Data Structure Client) A interface analysis 1 A implementation analysis 3 B interface developers communicate with system via interfaces analysis 2 precision: B implementation within data structures Checking that abstract structures reflect implementations

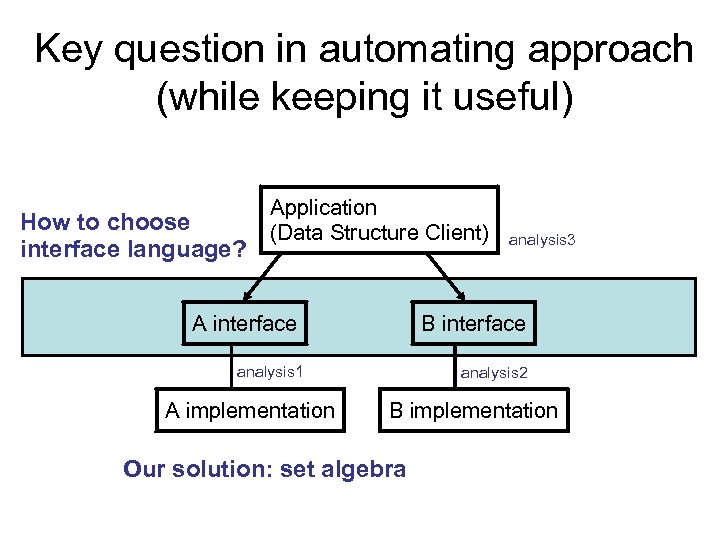Key question in automating approach (while keeping it useful) How to choose interface language? Application (Data Structure Client) A interface B interface analysis 1 A implementation analysis 3 analysis 2 B implementation Our solution: set algebra

Set algebra as interface language Useful: express key data structure properties – disjointness (A Å B = ; ), inclusion (A µ B) – insertion (S’ = S [ x), removal (S’ = S x) – conceptual object state • initialization, sequencing of API operations • symbolic notations for hierarchical state charts Verifiable: on both sides of set abstraction – typestate techniques for interface uses – shape analyses for interface implementations

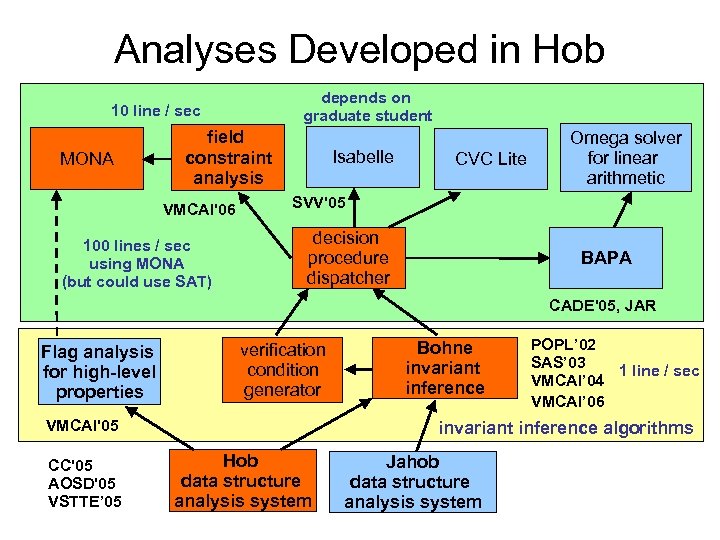
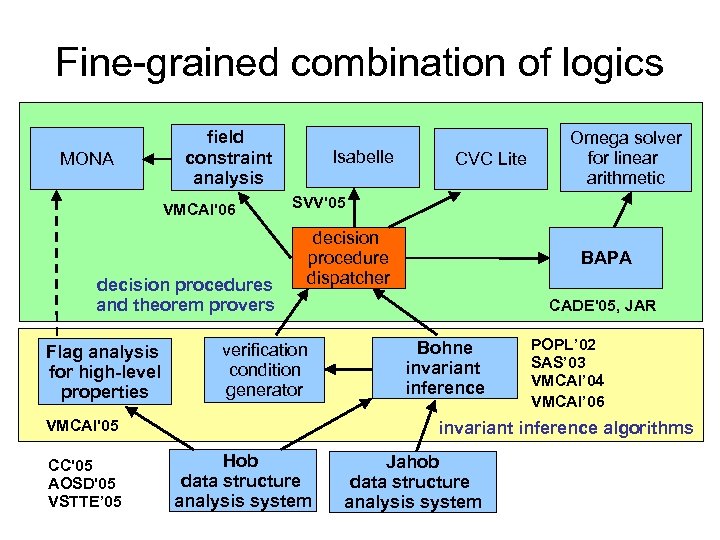
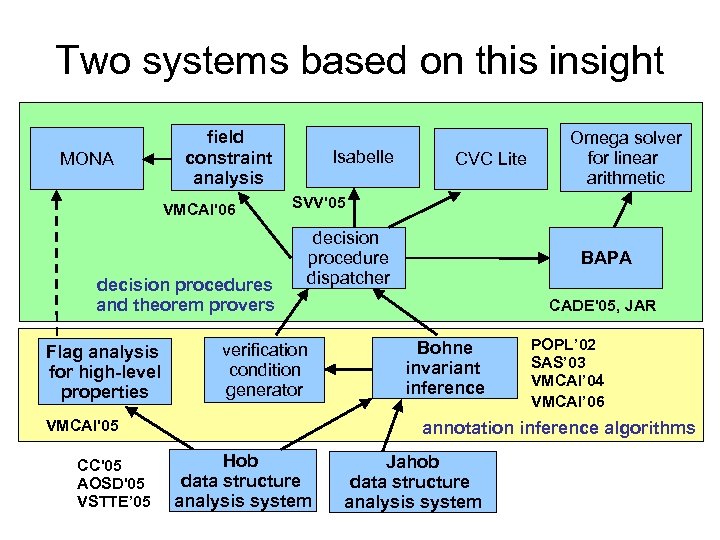Two systems based on this insight MONA field constraint analysis VMCAI'06 decision procedures and theorem provers Flag analysis for high-level properties Isabelle SVV'05 decision procedure dispatcher verification condition generator VMCAI'05 CC'05 AOSD'05 VSTTE’ 05 CVC Lite Omega solver for linear arithmetic BAPA CADE'05, JAR Bohne invariant inference POPL’ 02 SAS’ 03 VMCAI’ 04 VMCAI’ 06 annotation inference algorithms Hob data structure analysis system Jahob data structure analysis system

Outline Goal: verify data structure consistency Our approach through an example Bohne: one of the analyses in our system Current status and ongoing work Future work

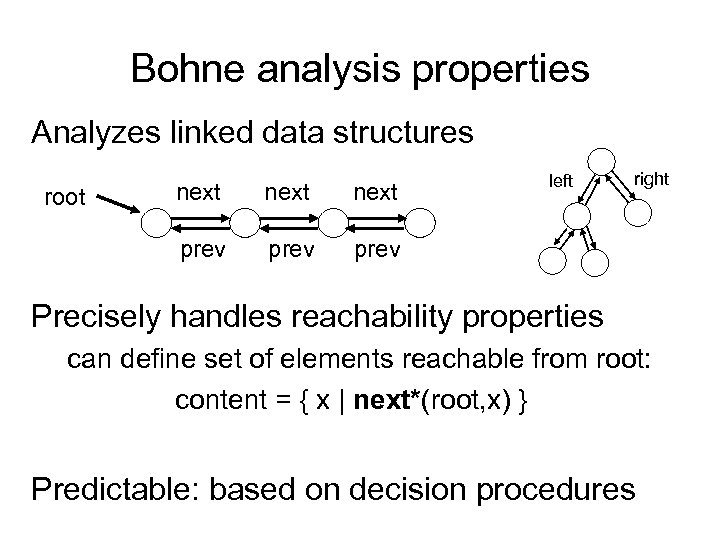Bohne analysis properties Analyzes linked data structures next prev root prev left right prev Precisely handles reachability properties can define set of elements reachable from root: content = { x | next*(root, x) } Predictable: based on decision procedures

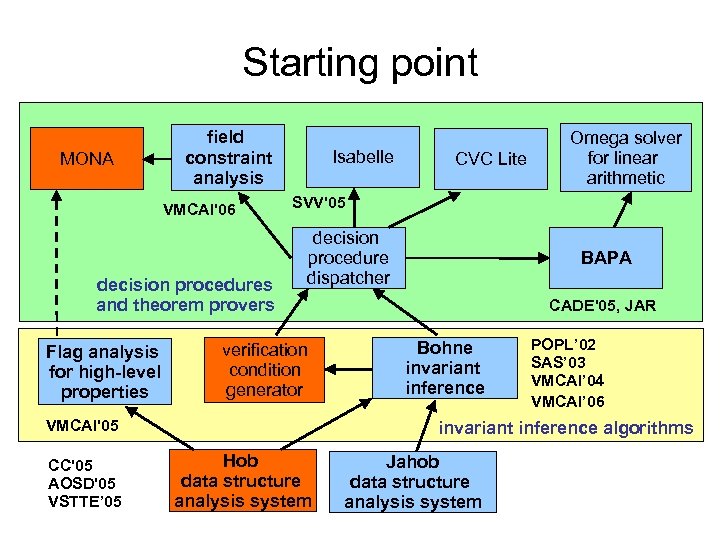Starting point MONA field constraint analysis VMCAI'06 decision procedures and theorem provers Flag analysis for high-level properties Isabelle SVV'05 decision procedure dispatcher verification condition generator VMCAI'05 CC'05 AOSD'05 VSTTE’ 05 CVC Lite Omega solver for linear arithmetic BAPA CADE'05, JAR Bohne invariant inference POPL’ 02 SAS’ 03 VMCAI’ 04 VMCAI’ 06 invariant inference algorithms Hob data structure analysis system Jahob data structure analysis system

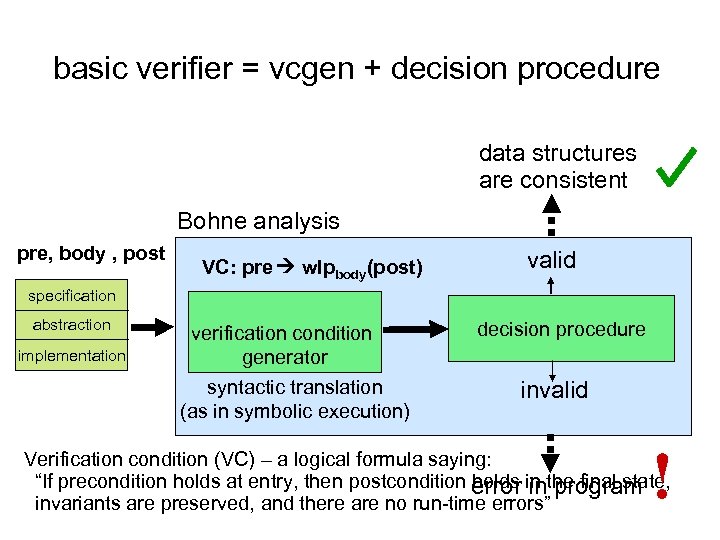basic verifier = vcgen + decision procedure data structures are consistent Bohne analysis pre, body , post VC: pre wlpbody(post) valid specification abstraction implementation verification condition generator syntactic translation (as in symbolic execution) decision procedure invalid ! Verification condition (VC) – a logical formula saying: “If precondition holds at entry, then postcondition error in the final state, holds in program invariants are preserved, and there are no run-time errors”

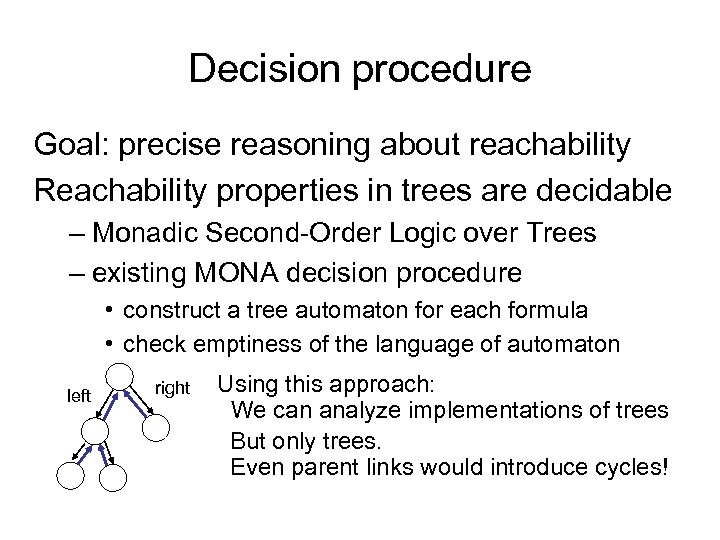Decision procedure Goal: precise reasoning about reachability Reachability properties in trees are decidable – Monadic Second-Order Logic over Trees – existing MONA decision procedure • construct a tree automaton for each formula • check emptiness of the language of automaton left right Using this approach: We can analyze implementations of trees But only trees. Even parent links would introduce cycles!

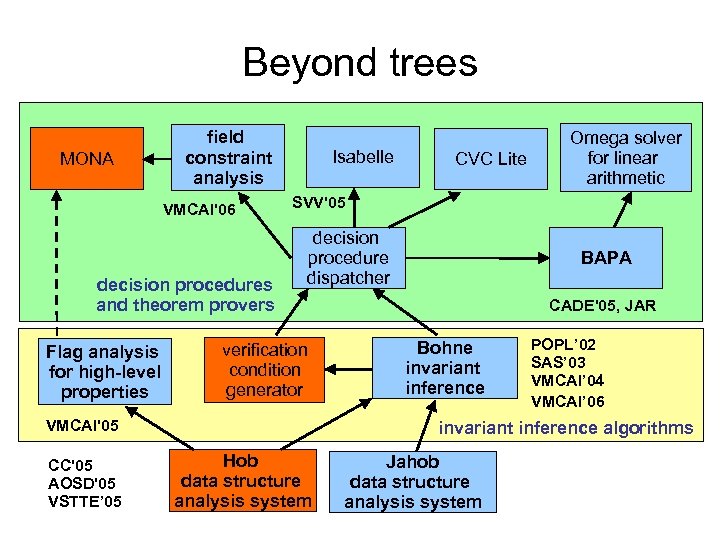Beyond trees MONA field constraint analysis VMCAI'06 decision procedures and theorem provers Flag analysis for high-level properties Isabelle SVV'05 decision procedure dispatcher verification condition generator VMCAI'05 CC'05 AOSD'05 VSTTE’ 05 CVC Lite Omega solver for linear arithmetic BAPA CADE'05, JAR Bohne invariant inference POPL’ 02 SAS’ 03 VMCAI’ 04 VMCAI’ 06 invariant inference algorithms Hob data structure analysis system Jahob data structure analysis system

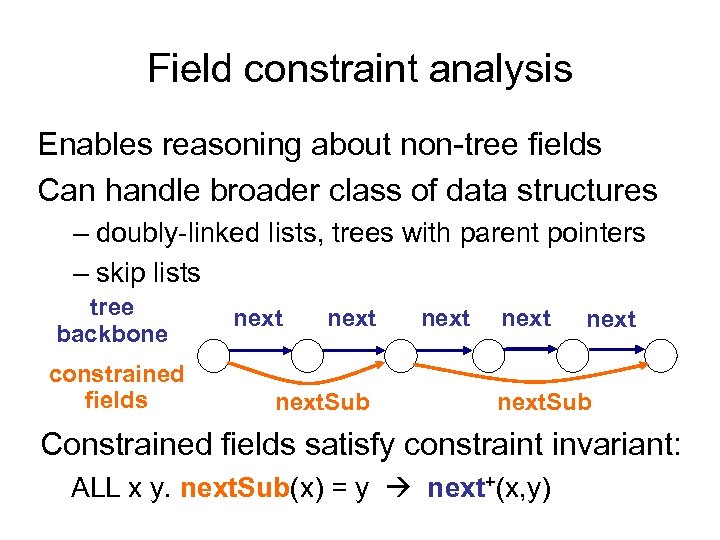Field constraint analysis Enables reasoning about non-tree fields Can handle broader class of data structures – doubly-linked lists, trees with parent pointers – skip lists tree backbone constrained fields next next. Sub Constrained fields satisfy constraint invariant: ALL x y. next. Sub(x) = y next+(x, y)

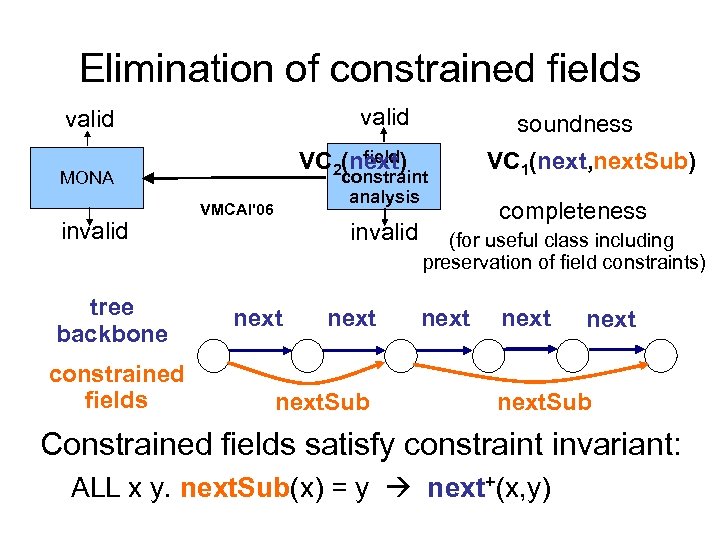Elimination of constrained fields valid field VC 2(next) constraint analysis MONA invalid tree backbone constrained fields soundness VMCAI'06 invalid next. Sub VC 1(next, next. Sub) completeness (for useful class including preservation of field constraints) next. Sub Constrained fields satisfy constraint invariant: ALL x y. next. Sub(x) = y next+(x, y)

Elimination of constrained fields Previous approaches – constraining formula must be deterministic We allow arbitrary constraint formulas – fields need not be uniquely given by backbone tree backbone constrained fields next next. Sub Constrained fields satisfy constraint invariant: ALL x y. next. Sub(x) = y next+(x, y)

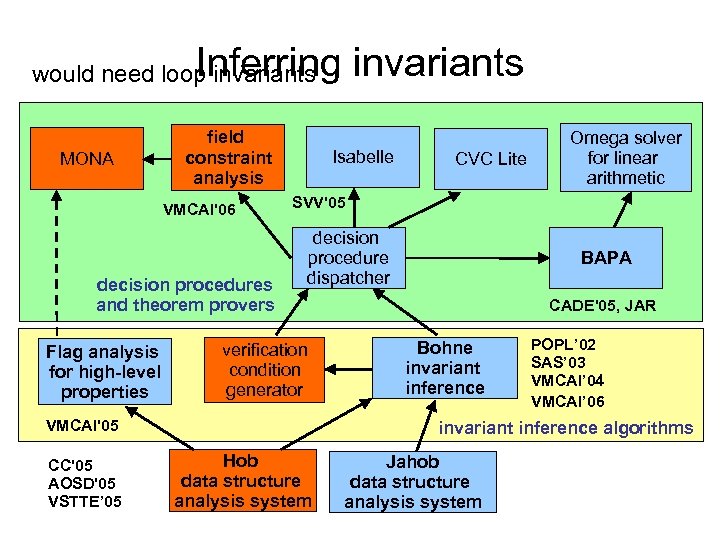Inferring invariants would need loop invariants MONA field constraint analysis VMCAI'06 decision procedures and theorem provers Flag analysis for high-level properties Isabelle SVV'05 decision procedure dispatcher verification condition generator VMCAI'05 CC'05 AOSD'05 VSTTE’ 05 CVC Lite Omega solver for linear arithmetic BAPA CADE'05, JAR Bohne invariant inference POPL’ 02 SAS’ 03 VMCAI’ 04 VMCAI’ 06 invariant inference algorithms Hob data structure analysis system Jahob data structure analysis system

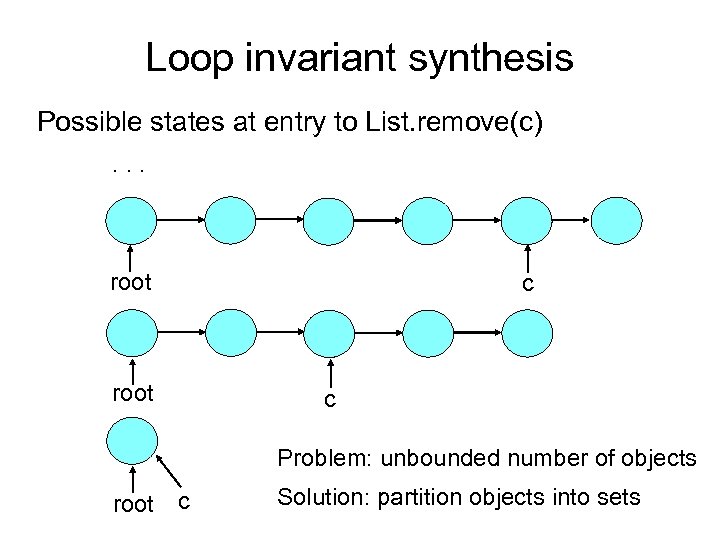Loop invariant synthesis Possible states at entry to List. remove(c). . . root c Problem: unbounded number of objects root c Solution: partition objects into sets

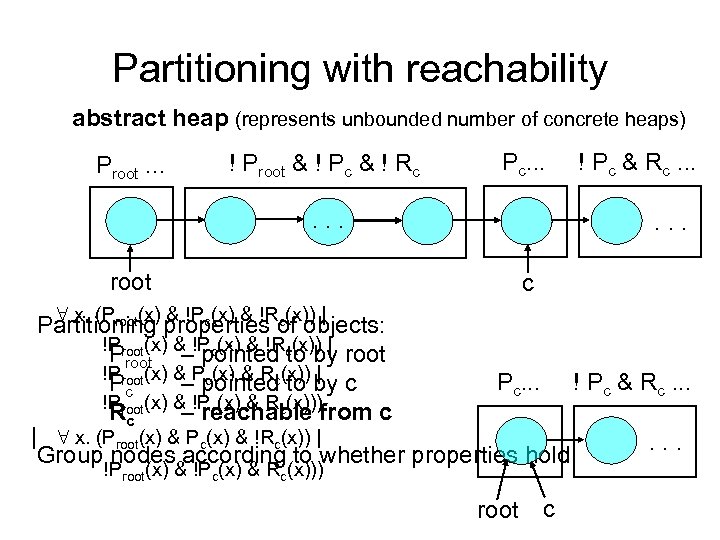Partitioning with reachability abstract heap (represents unbounded number of concrete heaps) Proot. . . ! Proot & ! Pc & ! Rc Pc. . root 8 x. (P ! Pc & Rc. . . c (x) & !P (x) & !R (x)) | root c c Partitioning properties of objects: !Proot(x) & !Pc(x) & !Rc(x)) | Proot – pointed to by root !Proot(x) & Pc(x) & Rc(x)) | Pc. . . ! Pc & Rc. . . Pc – pointed to by c !Proot(x) & !Pc(x) & Rc(x))) Rc – reachable from c | 8 x. (Proot(x) & Pc(x) & !Rc(x)) |. . . Group nodes according to whether properties hold !Proot(x) & !Pc(x) & Rc(x))) root c

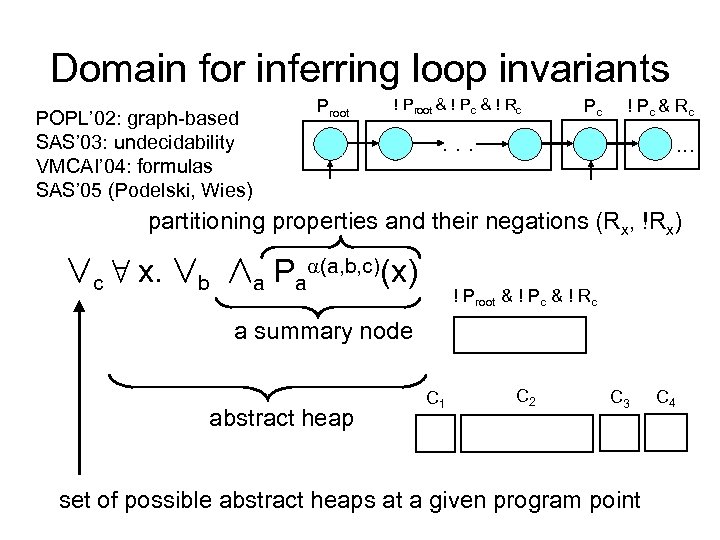Domain for inferring loop invariants POPL’ 02: graph-based SAS’ 03: undecidability VMCAI’ 04: formulas SAS’ 05 (Podelski, Wies) Proot ! Proot & ! Pc & ! Rc Pc ! P c & Rc . . . partitioning properties and their negations (Rx, !Rx) Çc 8 x. Çb Æa Pa (a, b, c)(x) ! Proot & ! Pc & ! Rc a summary node abstract heap C 1 C 2 C 3 set of possible abstract heaps at a given program point C 4

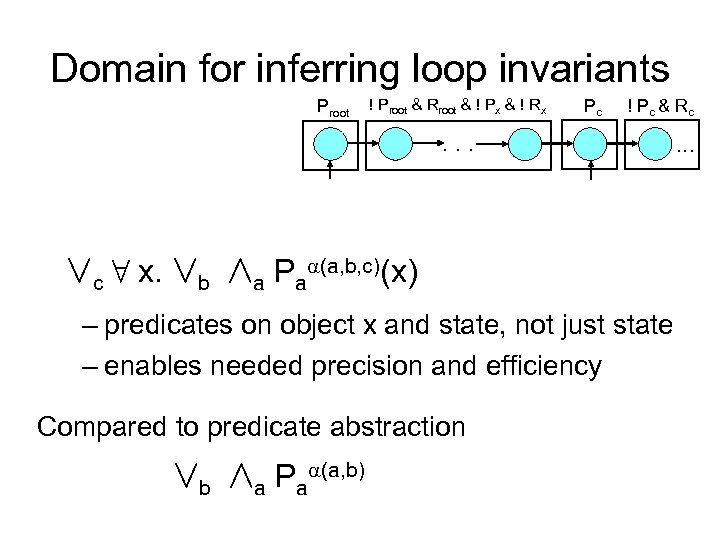Domain for inferring loop invariants Proot ! Proot & Rroot & ! Px & ! Rx Pc ! P c & Rc . . . Çc 8 x. Çb Æa Pa (a, b, c)(x) – predicates on object x and state, not just state – enables needed precision and efficiency Compared to predicate abstraction Çb Æa Pa (a, b) . . .

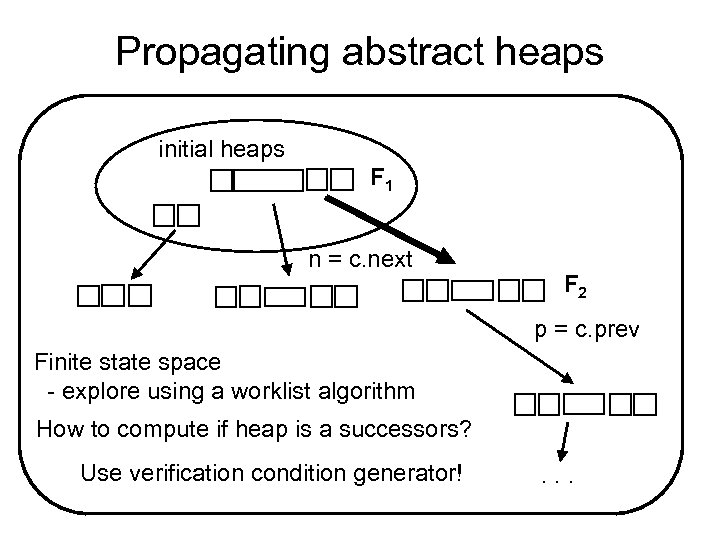Propagating abstract heaps initial heaps F 1 n = c. next F 2 p = c. prev Finite state space - explore using a worklist algorithm How to compute if heap is a successors? Use verification condition generator! . . .

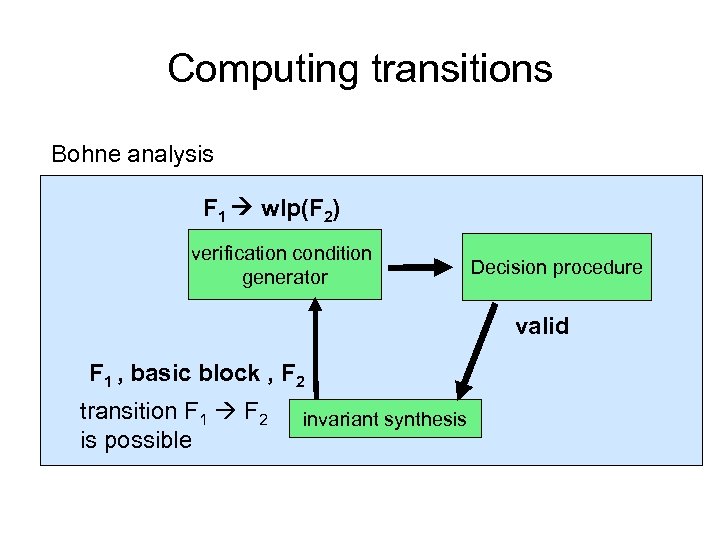Computing transitions Bohne analysis F 1 wlp(F 2) verification condition generator Decision procedure valid F 1 , basic block , F 2 transition F 1 F 2 is possible invariant synthesis

Making invariant synthesis feasible Naive algorithm: 2^2 n queries Reducing number of queries – transform each summary node independently (Cartesian abstraction) – avoid recomputation • precompute abstractions of transitions (generalization of Boolean programs) • precompute unsatisfiable conjunctions • ‘semantic’ caching of queries – auxiliary analysis to propagate true conjuncts Improvements crucial for making analysis feasible

Analyses Developed in Hob depends on graduate student 10 line / sec MONA field constraint analysis VMCAI'06 100 lines / sec using MONA (but could use SAT) Isabelle CVC Lite Omega solver for linear arithmetic SVV'05 decision procedure dispatcher BAPA CADE'05, JAR Flag analysis for high-level properties verification condition generator VMCAI'05 CC'05 AOSD'05 VSTTE’ 05 Bohne invariant inference POPL’ 02 SAS’ 03 1 line / sec VMCAI’ 04 VMCAI’ 06 invariant inference algorithms Hob data structure analysis system Jahob data structure analysis system

Outline Goal: verify data structure consistency Our approach through an example Bohne: one of the analyses in our system Current status – analyzed programs – ongoing work Future work

Minesweeper experience true init next prev is inverse of next is. Exposed false next is acyclic object is in hidden cells list iff initialized and is. Exposed is false

Verified properties meaningful to designers and end users disjoint(Hidden. content, Exposed. content) “A cell is never both hidden and exposed” – consistency needed to understand the game ! disjoint(Mined. content, Exposed. content) => game. Over “If a mined cell is exposed, the game is over” – defining property of the game

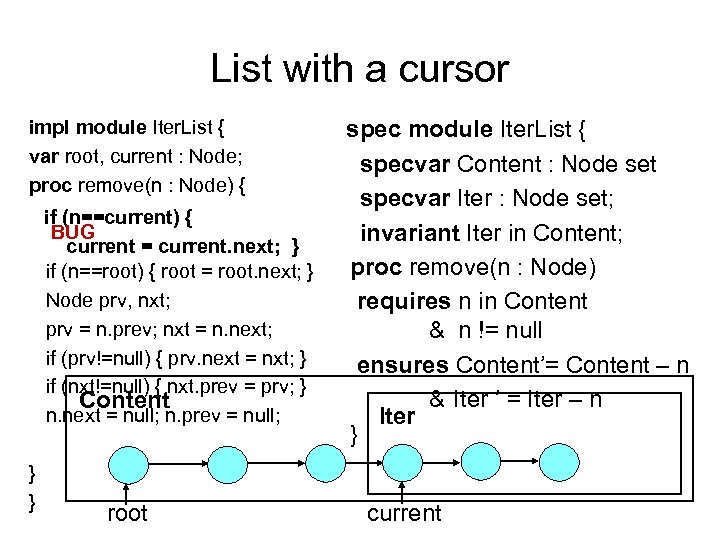List with a cursor impl module Iter. List { var root, current : Node; proc remove(n : Node) { if (n==current) { BUG current = current. next; } if (n==root) { root = root. next; } Node prv, nxt; prv = n. prev; nxt = n. next; if (prv!=null) { prv. next = nxt; } if (nxt!=null) { nxt. prev = prv; } Content n. next = null; n. prev = null; } } root spec module Iter. List { specvar Content : Node set specvar Iter : Node set; invariant Iter in Content; proc remove(n : Node) requires n in Content & n != null ensures Content’= Content – n & Iter ’ = Iter – n Iter } current

Verifying use of cursors List. open. Iter(); bool b = List. is. Last. Iter(); while (!b) { c = List. next. Iter(); View. draw. Cell(c); b = List. is. Last. Iter(); } iterator initialized before use no iteration past the end each cell visited exactly once spec module Iter. List { specvar Content, Iter : Node set; invariant Iter in Content; proc is. Last. Iter() returns b : bool ensures b' <=> (Iter ' = {}); proc next. Iter() returns n : Node requires Iter != { } modifies Iter ensures (n != null) & (n in Iter) & (Iter ' = Iter - n) & (n in Content); }

Further analyzed programs Water particle simulation: ordering of computation phases Web server: initialization, ordering, data structures – serving http: //hob. csail. mit. edu High-level properties – relationships between different data structures – none of individual analysis could handle alone Individual data structures: – trees (w/ parents), doubly-linked lists (w/ cursors) – skip lists, lists with cross pointers, array, priority queue Ongoing work: – turn-based strategy game, collection classes – operating system data structures

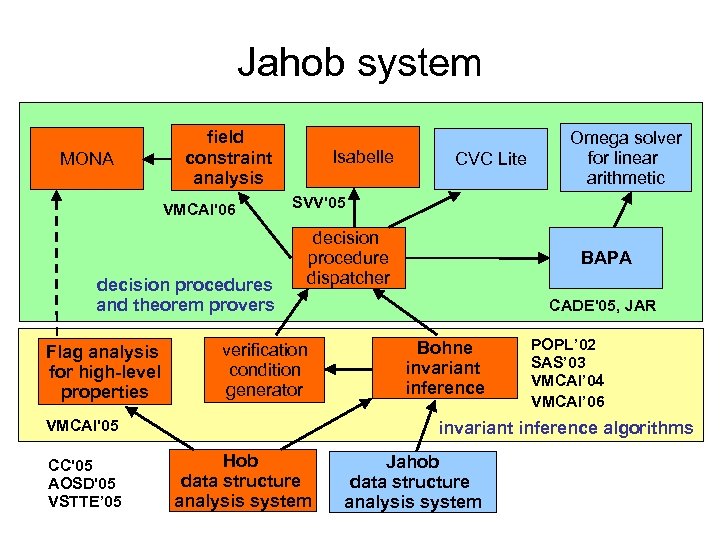Jahob system MONA field constraint analysis VMCAI'06 decision procedures and theorem provers Flag analysis for high-level properties Isabelle SVV'05 decision procedure dispatcher verification condition generator VMCAI'05 CC'05 AOSD'05 VSTTE’ 05 CVC Lite Omega solver for linear arithmetic BAPA CADE'05, JAR Bohne invariant inference POPL’ 02 SAS’ 03 VMCAI’ 04 VMCAI’ 06 invariant inference algorithms Hob data structure analysis system Jahob data structure analysis system

Jahob system Successor to Hob Goal: check data structures in more scenarios – richer interfaces and invariants • maps to specify association lists, hash tables • relations to specify unbounded number of instances • symbolic cardinality constraints on sets – future extension to other properties Implementation language: Java subset Specification language: Isabelle subset New specialized decision procedures

Fine-grained combination of logics MONA field constraint analysis VMCAI'06 decision procedures and theorem provers Flag analysis for high-level properties Isabelle SVV'05 decision procedure dispatcher verification condition generator VMCAI'05 CC'05 AOSD'05 VSTTE’ 05 CVC Lite Omega solver for linear arithmetic BAPA CADE'05, JAR Bohne invariant inference POPL’ 02 SAS’ 03 VMCAI’ 04 VMCAI’ 06 invariant inference algorithms Hob data structure analysis system Jahob data structure analysis system

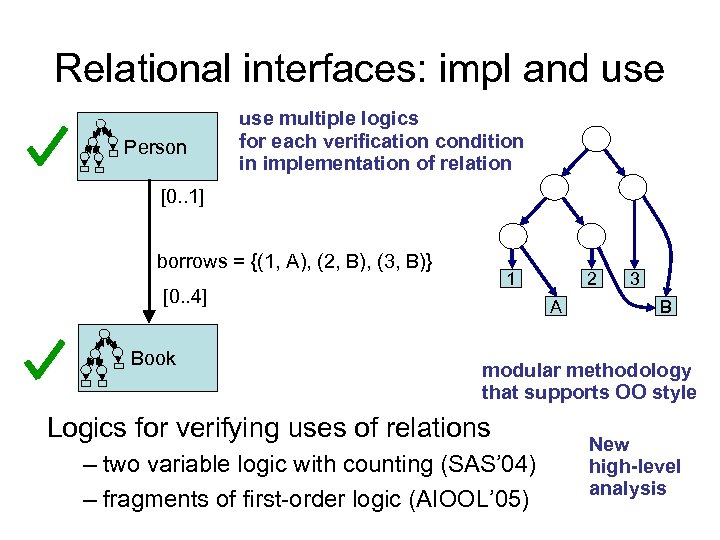Relational interfaces: impl and use Person use multiple logics for each verification condition in implementation of relation [0. . 1] borrows = {(1, A), (2, B), (3, B)} 1 [0. . 4] Book 2 A 3 B modular methodology that supports OO style Logics for verifying uses of relations – two variable logic with counting (SAS’ 04) – fragments of first-order logic (AIOOL’ 05) New high-level analysis

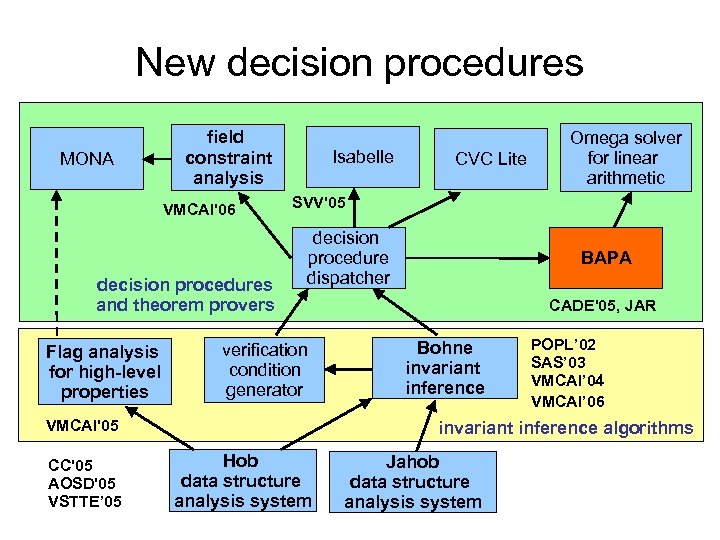New decision procedures MONA field constraint analysis VMCAI'06 decision procedures and theorem provers Flag analysis for high-level properties Isabelle SVV'05 decision procedure dispatcher verification condition generator VMCAI'05 CC'05 AOSD'05 VSTTE’ 05 CVC Lite Omega solver for linear arithmetic BAPA CADE'05, JAR Bohne invariant inference POPL’ 02 SAS’ 03 VMCAI’ 04 VMCAI’ 06 invariant inference algorithms Hob data structure analysis system Jahob data structure analysis system

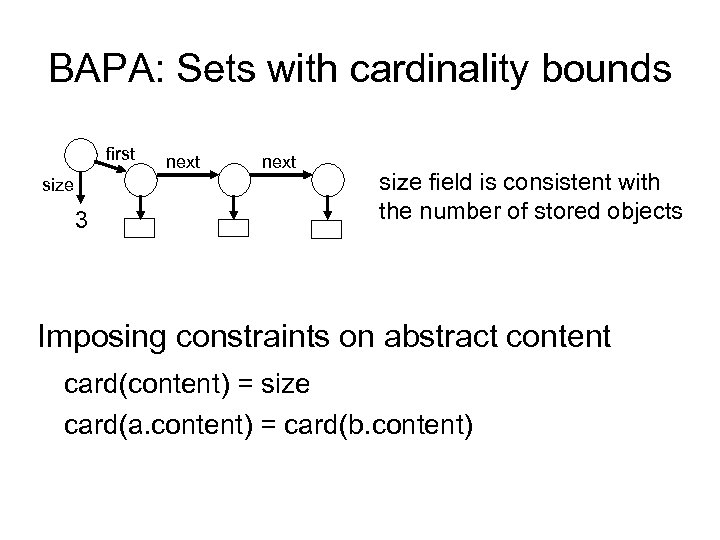BAPA: Sets with cardinality bounds first size 3 next size field is consistent with the number of stored objects Imposing constraints on abstract content card(content) = size card(a. content) = card(b. content)

Boolean Algebra with Presburger Arithmetic S : : = V | S 1 [ S 2 | S 1 Å S 2 | S 1 n S 2 T : : = k | C | T 1 + T 2 | T 1 – T 2 | C¢T | card(S) A : : = S 1 = S 2 | S 1 µ S 2 | T 1 = T 2 | T 1 < T 2 F : : = A | F 1 Æ F 2 | F 1 Ç F 2 | : F | 9 S. F | 9 k. F Not widely known, but natural extension of BAs Gave first complexity bound (CADE'05, JAR) – quantifier elimination algorithm (as in LICS’ 03) Recent results (see technical report, submissions): – first PSPACE algorithm for quantifier-free fragment – identified new useful polynomial-time fragment

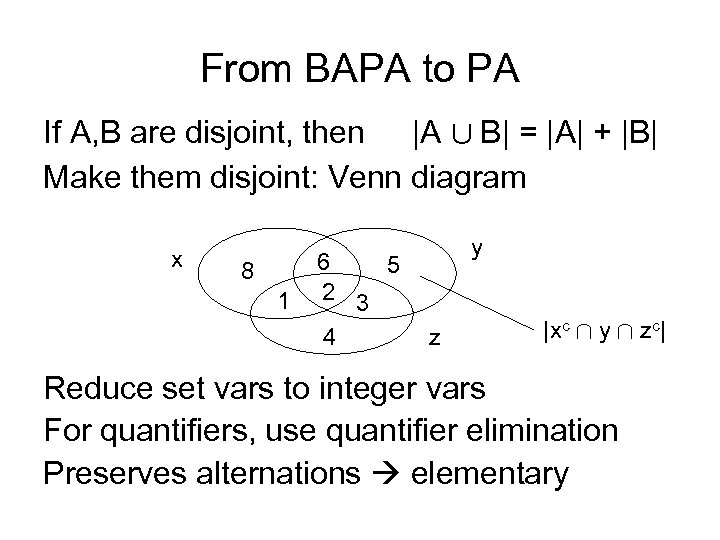From BAPA to PA If A, B are disjoint, then |A [ B| = |A| + |B| Make them disjoint: Venn diagram x 8 1 6 5 2 3 4 y z |xc Å y Å zc| Reduce set vars to integer vars For quantifiers, use quantifier elimination Preserves alternations elementary

Quantifier-free BAPA Previous technique gives NEXPTIME Can do it in PSPACE: – analyze resulting equations exponentially many variables polynomially many equations finite model property: solutions singly exp. – guess sizes of sets – use alternating PTIME algorithm to check them Also identified a tree-like fragment, in PTIME

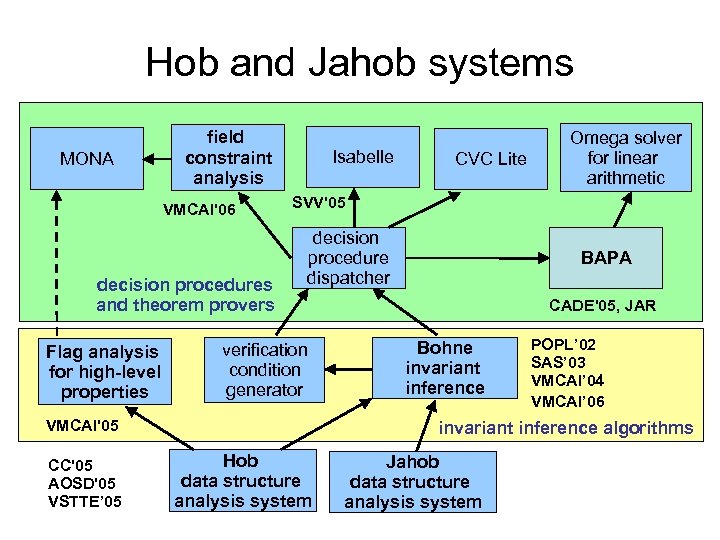Hob and Jahob systems MONA field constraint analysis VMCAI'06 decision procedures and theorem provers Flag analysis for high-level properties Isabelle SVV'05 decision procedure dispatcher verification condition generator VMCAI'05 CC'05 AOSD'05 VSTTE’ 05 CVC Lite Omega solver for linear arithmetic BAPA CADE'05, JAR Bohne invariant inference POPL’ 02 SAS’ 03 VMCAI’ 04 VMCAI’ 06 invariant inference algorithms Hob data structure analysis system Jahob data structure analysis system

Future work: roadmap So far: conformance of code to model (specification) Next: address the construction of models – counterexamples for models (Alloy, FSE’ 05) – testing, run-time checking of specifications – efficient execution of declarative specifications Fostering adoption of specifications – inference, syntax, quantifiers, defaults, templates Deploy within software development environments Integrate domain-specific knowledge – operating systems, games, embedded systems

Related work Comparison to modular set-based analysis – we are similarly • modular (but contracts: mutation, heap vs higher-order) • use sets and relations (of objects, not terms) note: LICS’ 03 – we also have • • data abstraction: public and private contracts, abst funs flow sensitivity, mutation: typestate shape properties: relationships between typestates different analyses in different modules – but so far no: higher order functions, contract inference, two-level constraints, IDE

Related work Shape analysis – Jones, Muchnik ’ 79: memory optimizations – Larus, Hilfinger’ 88: detecting conflicts in memory accesses – Hendren, Nicolau ’ 90: parallelization, connection analysis – Chase, Wegman, Zadeck’ 90: allocation-site model – Klarlund, Schwartzbach’ 93: graph types – Deutsch ’ 94: symbolic bounds on paths – Fradet, Metayer ’ 97: graph-grammars – Sagiv, Reps, Wilhelm ’ 99: 3 -valued framework – Lev-Ami, Sagiv ’ 00: TVLA implementation – Moeller, Schwartzbach ’ 01: PALE based on MONA – Yorsh, Reps, Sagiv ’ 04: assume/guarantee reasoning for 3 VL – Mc. Peak, Necula ’ 05: local pointer properties – Rugina, Hacket’ 05: region-based – Lee, Yang, Yi’ 05: combining three-valued and grammar-based

Related work Model checking: – Holzmann ’ 97: SPIN – Burch, Clarke, Long, Mc. Millan, Dill ’ 92: SMV – Pisman, Pnueli ’ 01: non-regular infinite state systems Predicate abstraction – extracting models – Graf, Saidi ’ 97: using PVS – Ball, Podelski ’ 01: Cartesian abstraction – Ball, Majumdar, Millstein, Rajamani ’ 01: SLAM – Henzinger, Jhala, Sutre’ 02: BLAST – Flanagan, Qadeer ’ 02: use of Skolem constants – Lahiri, Seshia, Bryant ’ 04: UCLID, indexed predicates – Balaban, Pnueli, Zuck ’ 05: small models for lists – Bingham, Rakamaric’ 06: abstraction of lists – Lahiri, Qadeer ’ 06: lists and data properties

Related work Decision procedures and theorem provers – Barrett, Berezin’ 04: CVC Lite – Detlef, Nelson, Saxe’ 03: Simplify – Ball, Lahiri, Musuvathi ’ 05: Zap – Thatcher, Wright’ 68: MSOL over finite trees – Klarlund, Moeller, Schwartzbach’ 00: MONA – Yorsh, Rabinovich, Sagiv, Meyer, Bouajjani’ 06: reachability logic – BAPA: Feferman, Vaught’ 59; Zarba’ 04, ’ 05 – Voronkov’ 95: Vampire, Weidenbach’ 01: Spass – Gordon’ 85: HOL, Pfenning’ 91: LF, Coquand, Huet’ 85: Coq – Constable, Allen, Bromley, Cleaveland, Cremer, Harper, Howe, Knoblock, Mendler, Panangaden, Sasaki, Smith’ 86: Nu. PRL – Gray, Hickey, Nogin, Tapus: Meta. PRL – Kaufmann, Manolios, Moore ’ 00: ACL 2 – Nipkow, Paulson, Wenzel’ 02: Isabelle

Related work Program verification systems – King ’ 70, Deutsch’ 73, Suzuki’ 73, Nelson’ 81, Guttag, Horning’ 93 – Good, Akers, Smith ’ 86: Gypsy – Jones’ 86: VDM – Abrial, Lee, Neilson, Scharbach, Soerensen’ 91: B method – Owre, Shankar, Rushby, Stringer-Calvert: PVS – Ahrendt, Baar, Beckert, Giese, Habermalz, Haehnle, Menzel, Schmitt’ 00: Ke. Y – Foulger, King’ 01: SPARK Ada – Flanagan, Leino, Lilibridge, Nelson, Saxe, Stata‘ 02: ESC/Java – Marche, Paulin-Mohring, Urbain’ 03: Krakatoa – Breunesse, Poll’ 05: model fields in JML – Barnett, De. Line, Jacobs, Fähndrich, Leino, Schulte, Venter’ 05: Spec# – Leino, Mueller’ 06: model fields in Spec#

Conclusions Goal: statically verify data structure consistency Hob system: language, framework, analyses – specification language based on sets – new shape analysis, new high-level analysis – analyzed minesweeper, water, web server • detailed data structure properties: trees, arrays, . . . • properties meaningful to users of the system Jahob system – richer specification language with relations – new decision procedures and analyses

Related work Array bounds checking – Bodik, Gupta, Sarkar ’ 00: demand-driven – Rugina, Rinard ’ 00: bounds and region analysis Pointer analyses – Steensgaard ’ 96: points-to in almost linear time – Andersen’ 94: inclusion constraints – Fähndrich, Rehof, Das ’ 00: instantiation constraints – Salcianu, Rinard ’ 05: side-effect analysis – Sridharan, Gopan, Shan, Bodik ’ 05: demand-driven – Sridharan, Bodik ’ 06: refinement-based

Cost of analyzing data structures Doubly exponential state space Non-elementary decision procedure Mutable reversal of list using a loop content ’ = content, structure remains acyclic list 5 seconds 2 -level skip list insertion content ’ = content [ {x}, structure remains skip list 35 seconds Insertion into parent tree content ’ = content [ {x} , structure remains parent tree 83 seconds

Related work Type systems – – Freeman, Pfenning ’ 91: refinement types Xi, Pfenning ’ 99: dependent ML Harren, Necula’ 05: dependent types in typed assembly Smith, Walker, Morrisett ’ 00: alias types Typestate systems – – Strom, Yemini ’ 86: typestate for initialization Fahndrich, De. Line ’ 01 ’ 04: finite state protocols Das, Lerner, Seigle ’ 02: typestate inference Ramalingam, Warshavsky, Field, Goyal, Sagiv ’ 02

Related work Bug finding and dynamic specification synthesis – Jackson, Vaziri ’ 00: finding bugs in code with Alloy – Taghdiri ’ 04: counterexample-driven refinement – Xie, Aiken ’ 05: Saturn – Evans ’ 94: LCLint – Engler, Musuvathi’ 00: metacompilation – Hovemeyer, Pugh ’ 04: Find. Bugs – Boyapati, Khurshid, Marinov ’ 02: Korat – Sen, Marinov, Agha: CUTE – Ernst, Czeisler, Griswold, Notkin’ 00: dynamic invariant inference – Ammons, Bodik, Larus ’ 02: dynamic finite state inference

Additional details and topics High-level analysis using set algebra Boolean algebra with Presburger arithmetic Relational reasoning about datatypes Decidability of structural subtyping Two-variable logic and spatial conjunction