Modular Information Aggregation with Combinatorial Prediction Markets Robin

Modular Information Aggregation with Combinatorial Prediction Markets Robin Hanson Department of Economics George Mason University

Weather Forecasting • • A Canonical Forecasting Arena Many public standardized forecasts Fast feedback, so lots of stats Forecasting analysis pioneer – methods, validation, aggregation, etc. • Place to try out forecasting innovations?

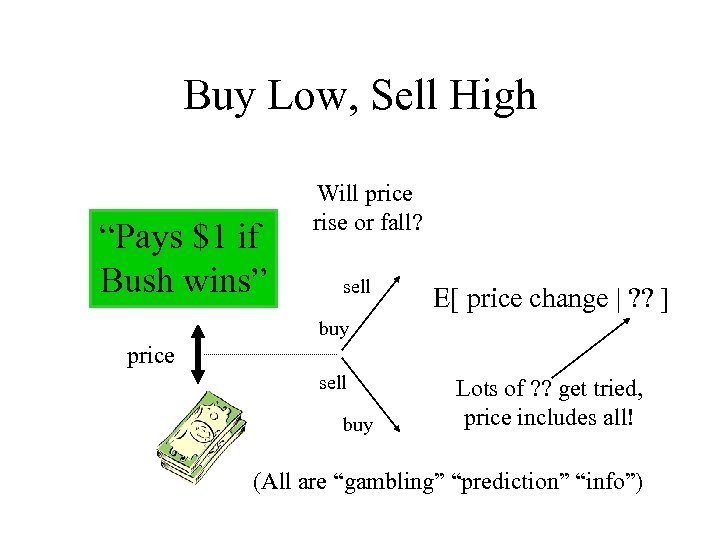
Buy Low, Sell High “Pays $1 if Bush wins” Will price rise or fall? sell E[ price change | ? ? ] buy price sell buy Lots of ? ? get tried, price includes all! (All are “gambling” “prediction” “info”)

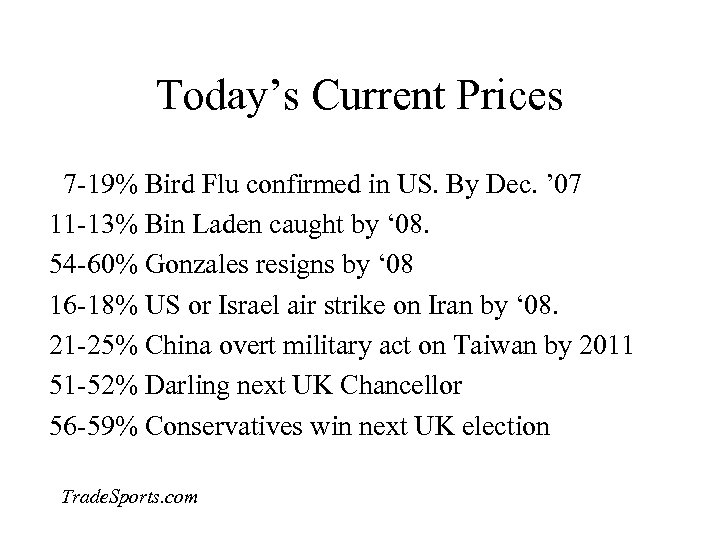
Today’s Current Prices 7 -19% Bird Flu confirmed in US. By Dec. ’ 07 11 -13% Bin Laden caught by ‘ 08. 54 -60% Gonzales resigns by ‘ 08 16 -18% US or Israel air strike on Iran by ‘ 08. 21 -25% China overt military act on Taiwan by 2011 51 -52% Darling next UK Chancellor 56 -59% Conservatives win next UK election Trade. Sports. com

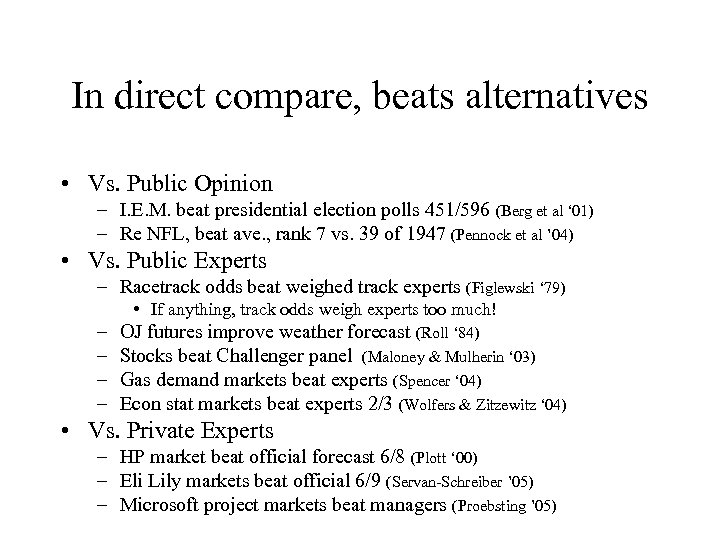
In direct compare, beats alternatives • Vs. Public Opinion – I. E. M. beat presidential election polls 451/596 (Berg et al ‘ 01) – Re NFL, beat ave. , rank 7 vs. 39 of 1947 (Pennock et al ’ 04) • Vs. Public Experts – Racetrack odds beat weighed track experts (Figlewski ‘ 79) • If anything, track odds weigh experts too much! – – OJ futures improve weather forecast (Roll ‘ 84) Stocks beat Challenger panel (Maloney & Mulherin ‘ 03) Gas demand markets beat experts (Spencer ‘ 04) Econ stat markets beat experts 2/3 (Wolfers & Zitzewitz ‘ 04) • Vs. Private Experts – HP market beat official forecast 6/8 (Plott ‘ 00) – Eli Lily markets beat official 6/9 (Servan-Schreiber ’ 05) – Microsoft project markets beat managers (Proebsting ’ 05)

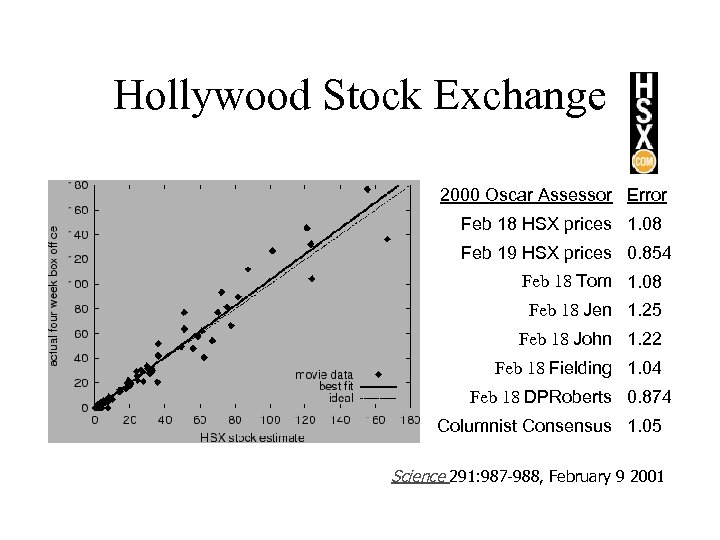
Hollywood Stock Exchange 2000 Oscar Assessor Error Feb 18 HSX prices 1. 08 Feb 19 HSX prices 0. 854 Feb 18 Tom 1. 08 Feb 18 Jen 1. 25 Feb 18 John 1. 22 Feb 18 Fielding 1. 04 Feb 18 DPRoberts 0. 874 Columnist Consensus 1. 05 Science 291: 987 -988, February 9 2001

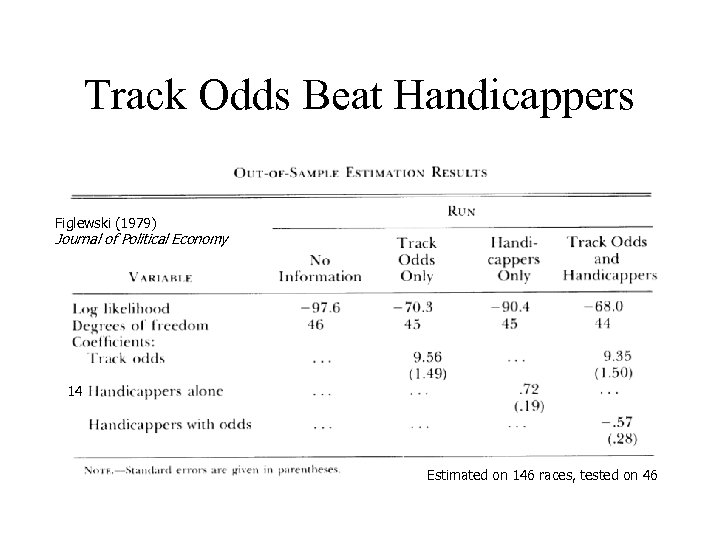
Track Odds Beat Handicappers Figlewski (1979) Journal of Political Economy 14 Estimated on 146 races, tested on 46

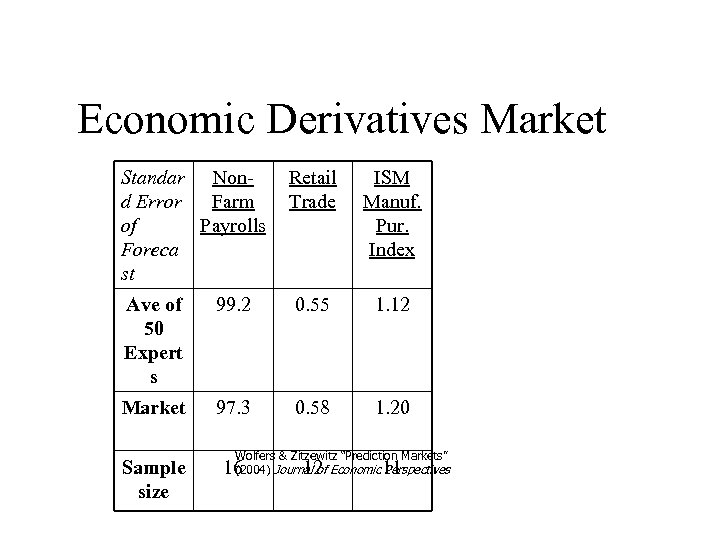
Economic Derivatives Market Standar Nond Error Farm of Payrolls Foreca st Retail Trade ISM Manuf. Pur. Index Ave of 50 Expert s 99. 2 0. 55 1. 12 Market 97. 3 0. 58 1. 20 Sample size Wolfers & Zitzewitz “Prediction Markets” (2004) Journal of Economic Perspectives 16 12 11

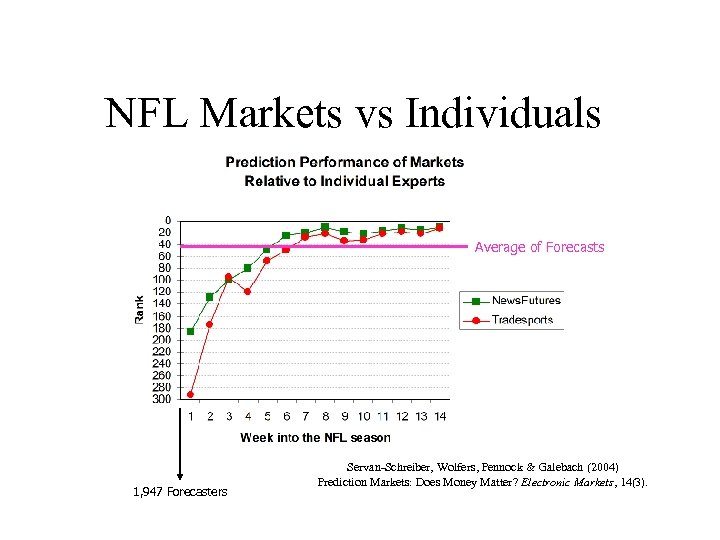
NFL Markets vs Individuals Average of Forecasts 1, 947 Forecasters Servan-Schreiber, Wolfers, Pennock & Galebach (2004) Prediction Markets: Does Money Matter? Electronic Markets, 14(3).

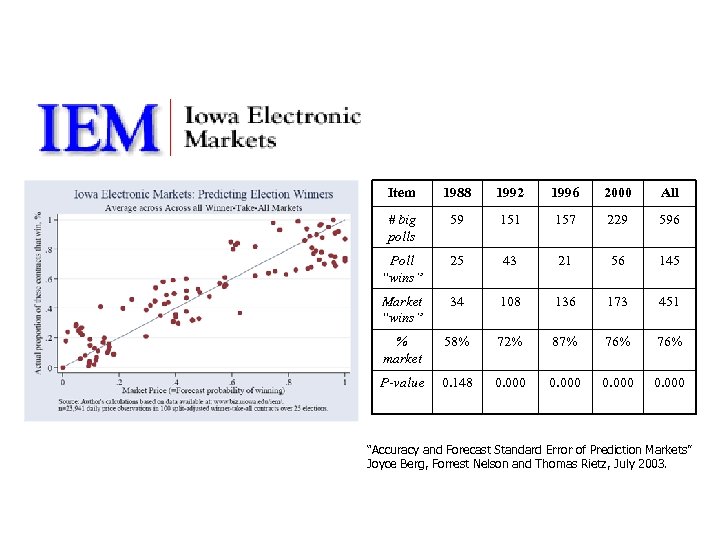
Item 1988 1992 1996 2000 All # big polls 59 151 157 229 596 Poll “wins” 25 43 21 56 145 Market “wins” 34 108 136 173 451 % market 58% 72% 87% 76% P-value 0. 148 0. 000 “Accuracy and Forecast Standard Error of Prediction Markets” Joyce Berg, Forrest Nelson and Thomas Rietz, July 2003.

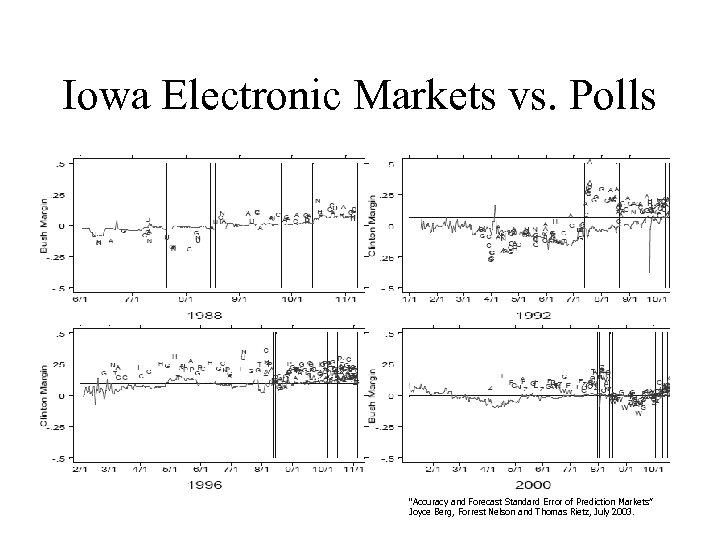
Iowa Electronic Markets vs. Polls “Accuracy and Forecast Standard Error of Prediction Markets” Joyce Berg, Forrest Nelson and Thomas Rietz, July 2003.

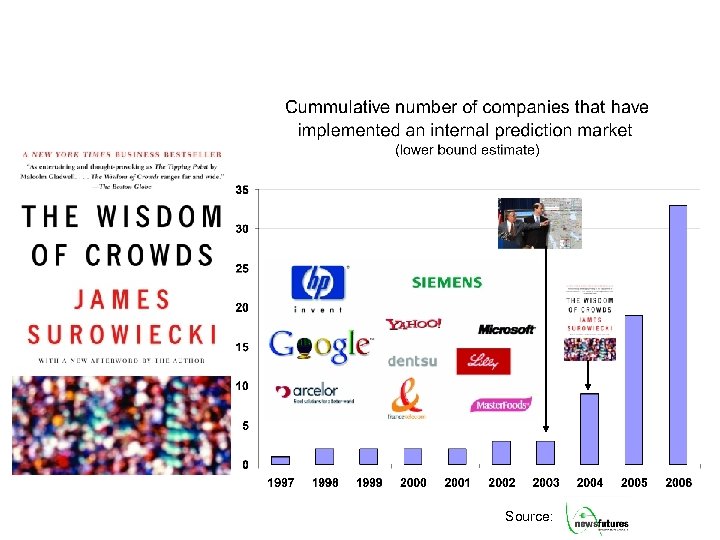
Source:

Prediction Markets Inputs For Same Status Quo Institution Outputs Compare!

Not Experts vs. Amateurs • Forecasting Institution Goal: – Given same participants, resources, topic – Want most accurate institution forecasts • Separate question: who let participate? – Can limit who can trade in market • Markets have low penalty for add fools – Hope: get more info from amateurs?

Advantages • • • Numerically precise Consistent across many issues Frequently updated Hard to manipulate Need not say who how expert on what At least as accurate as alternatives

Old Tech Meets New • To gain info, elicit probs p = {pi}i , Ep[x |A] (Let verify state i later, N/Q = people/questions) • Old tech (~1950+): Proper Scoring Rules N/Q 1: works well, N/Q 1: hard to combine • New tech (~1990+): Info/Predict Markets N/Q 1: works well, N/Q 1: thin markets • The best of both: Market Scoring Rules – modular, lab tests, compute issues, …

Old Tech: Proper Scoring Rules • When report r, state is i, reward is si(r) p = argmaxr i pi si(r), i pi si(p) 0 • Quadratic (G. Brier 1950) si 2 ri – k rk 2 • Logarithmic (I. Good ‘ 52) si log(ri) – Unique: reward = likelihood (R. Winkler 1969) • Offers info effort incentive (R. Clemen ‘ 02) – Stronger for simul. pick: pivot mech. (T. Page ‘ 88) • In principle, can elicit complex joint distributions • Long used in forecasting, test scoring, lab expers

Old Tech Issues Problems • Incentives • Number shy • Cognitive bias • Non risk-neutral • State-dependent utility • Combo explosion • Disagreements Solutions • Proper scoring rules • Prob wheel, word menu • Corrections • Lottery payoffs • Insurance game • Dependence network • Dictator per Q, ? ?

Opinion Pool “Impossibile” • Task: pool prob. T(A) from opinions pn(A) • Any 2 of IPP, MP, EB dictator (T= pd ) ! IPP = if A, B indep. in all pn , are indep. in T EB = commutes: pool, update on info MP = commutes: pool, coarsen states ( -field) (MP T = n=0 wn pn , with wn indep. of A) • Really want pool via belief origin theory – General solution: let best traders figure it out?

New Tech Issues Problems • Incentives • Shy, complex utility • Combo explosion • Who expert on what • Cognitive bias, pooling • Thin markets (N/Q <~1) • What is independent Solutions • Bet with each other • Same solutions • Self-select • Specialist traders • Market scoring rules • ? ?

Thin Market, No-Trade Problems • Trade requires coordination – In Time: waiting offers suffer adverse selection – In Assets: far more possible assets than trades • combo match call markets help some, but matching is NP-hard for all or nothing orders – If expect traders rare, don’t bother to offer • Most possible markets do not exist (also illegal) • No-trade among rational, info-motivated – Need fools, risk-hedgers, or outside subsidy

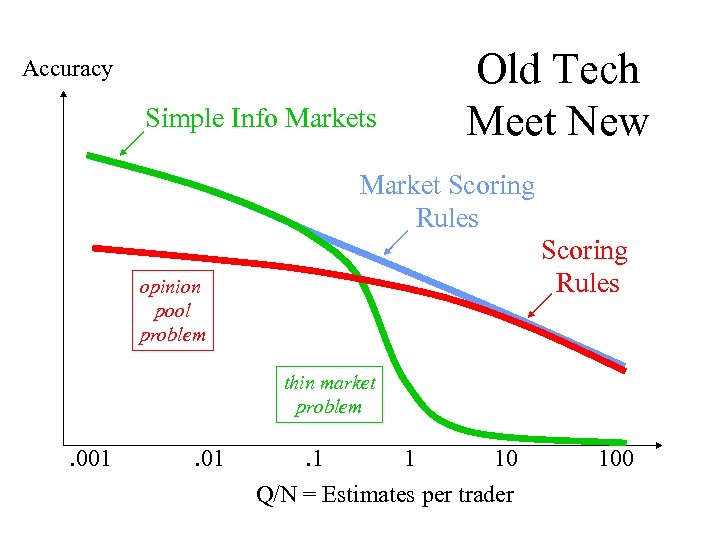
Accuracy Simple Info Markets opinion pool problem Old Tech Meet New Market Scoring Rules thin market problem . 001 . 1 1 10 Q/N = Estimates per trader 100

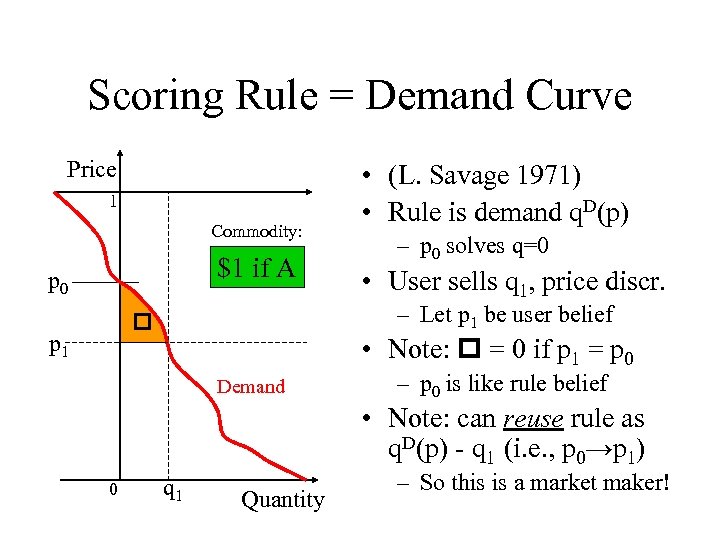
Scoring Rule = Demand Curve Price 1 Commodity: $1 if A p 0 – p 0 solves q=0 • User sells q 1, price discr. – Let p 1 be user belief p 1 • (L. Savage 1971) • Rule is demand q. D(p) • Note: = 0 if p 1 = p 0 Demand – p 0 is like rule belief • Note: can reuse rule as q. D(p) - q 1 (i. e. , p 0→p 1) 0 q 1 Quantity – So this is a market maker!

Market Scoring Rule (MSR) • MSRs act as scoring rules and info market makers – are sequentially reused combinatorial scoring rules • Score rule: user t faces $ rule: Dsi = si(pt) - si(pt-1) “Anyone can use scoring rule if pay off last user” • Automated market maker: price from net sales s $ ei if i – Tiny sale fee: pi(s) ei (si si+ei) $ s(1)-s(0) – Big sale fee: 01 i pi(s(t)) si´(t) dt – Log score rule gives: pi(s) = exp( si) / k exp( sk)

MSR Usage Concept • User browses current probabilities, expectations – Can set assumptions, browse other values given them – Can see market value of portfolio given assumptions • Upon finding an “odd” current value E(x|A) – Can see value’s price/trade history – Can see how far long/short are from past trades • User proposes new value to replace old – Told exact “bet” required to implement change – Can accept, and/or make book orders & trading agents

The Vision • Detailed consensus forecasts always visible re many locations, times, conditions, etc. • Authorized traders can change any estimates. – Possibly conditional on many other estimates. – Could write program to change many estimates. – At least until their account runs out. • Win if moved estimate closer to truth. • Consistent winners gain more resources. • Could even privatize, and/or let public try.

Laboratory Tests • Joint work with John Ledyard (Caltech), Takashi Ishida (Net Exchange) • Caltech students, get ~$30/session • 6 periods/session, 12 -15 minutes each • Trained in 3 var session, return for 8 var • Metric: Kulback-Leibler i qi log(pi /qi) distance from market prices to Bayesian beliefs given all group info

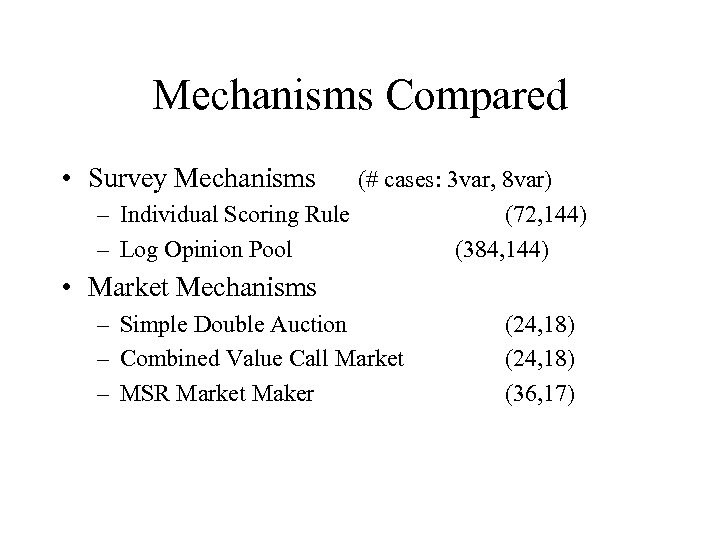
Mechanisms Compared • Survey Mechanisms (# cases: 3 var, 8 var) – Individual Scoring Rule (72, 144) – Log Opinion Pool (384, 144) • Market Mechanisms – Simple Double Auction – Combined Value Call Market – MSR Market Maker (24, 18) (36, 17)

Environments: Goals, Training • Want in Environment: – – – Many vars, few related, guess which Use both theory and data Few people, specialize in variable sets Can compute rational group estimates Explainable, fast, neutral • Training Environment: – – 3 binary variables X, Y, Z, 23 = 8 combos P(X=0) =. 3, P(X=Y) =. 2, P(Z=1)=. 5 3 people, see 10 cases of: AB, BC, AC Random map XYZ to ABC (Actually: X Z Y) Case 1 2 3 4 5 6 7 8 9 10 A 1 1 1 1 1 0 B - C 1 0 0 1 1 0 0 0 Sum: 9 - 3 B ---- C 4 --- Same A A -B -C --

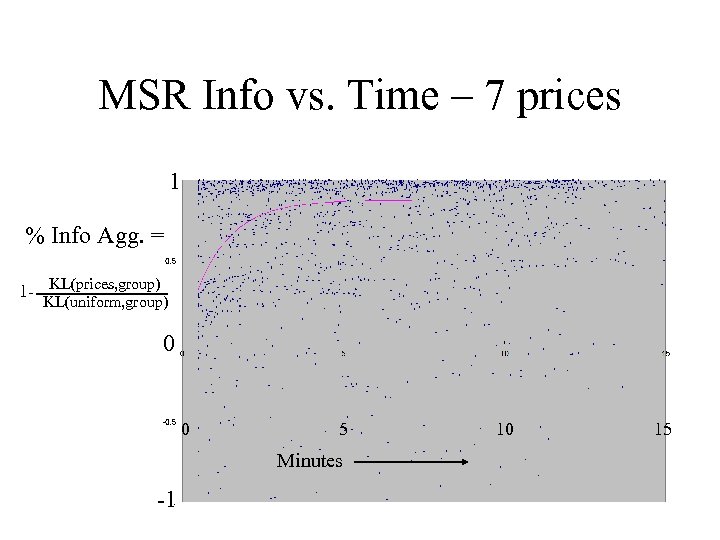
MSR Info vs. Time – 7 prices 1 % Info Agg. = 1 - KL(prices, group) KL(uniform, group) 0 0 5 10 15 Minutes -1

Experiment Environment (Really: W • 8 binary vars: STUVWXYZ Case A 1 0 8 = 256 combinations 2 1 • 2 3 0 • 20% = P(S=0) = P(S=T) 4 1 5 0 = P(T=U) = P(U=V) = … 6 1 7 0 = P(X=Y) = P(Y=Z) 8 1 9 1 • 6 people, each see 10 cases: 10 1 ABCD, EFGH, ABEF, Sum 6 CDGH, ACEG, BDFH Same A A - • random map STUVWXYZ B -C -to ABCDEFGH D -… V X S U Z Y T) B 1 0 0 0 C 0 0 1 1 1 0 0 0 D 1 1 1 1 1 E - F - G - H - 3 4 10 - - B 1 ---- C D 2 6 7 3 -4 -- -- E ----- F ----- G ----- H -----

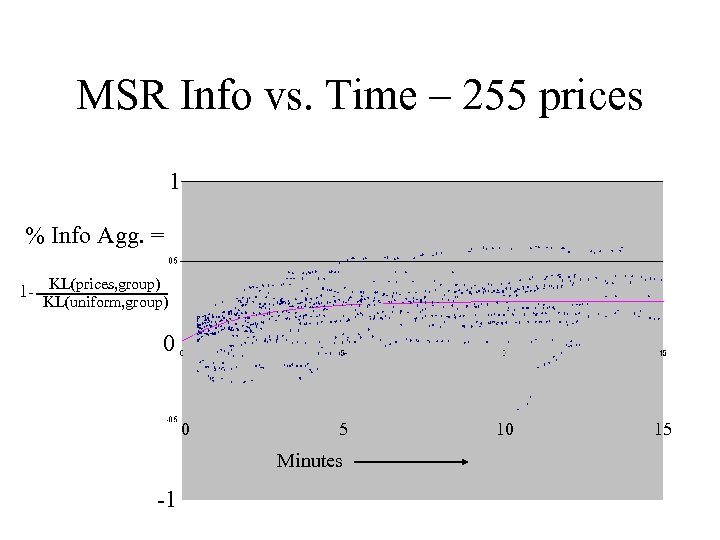
MSR Info vs. Time – 255 prices 1 % Info Agg. = 1 - KL(prices, group) KL(uniform, group) 0 0 5 10 15 Minutes -1

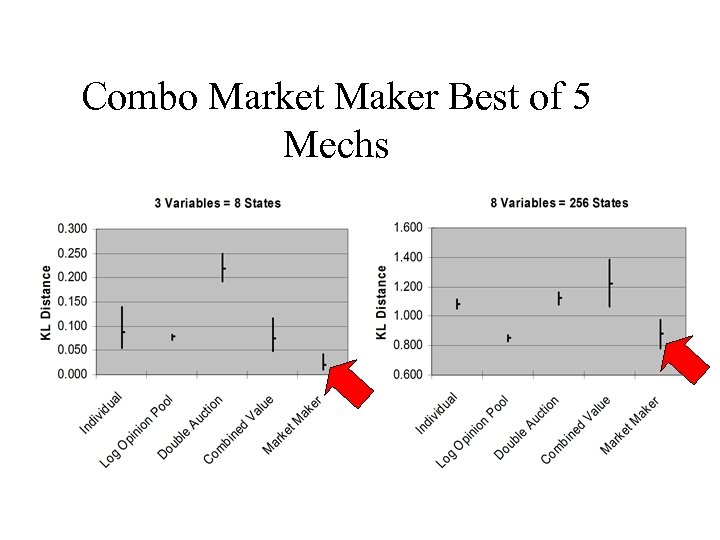
Combo Market Maker Best of 5 Mechs

Experiment Conclusions • Experiments on complex info problems – Bayesian estimates far too high a standard • 7 indep. prices from 3 people in < 4 minutes – Simple DA < Indiv. Score Rule ~ Opinion Pool ~ Combined Value < Market Scoring Rule • 255 indep. prices from 6 people in < 4 min. – Combined Value ~ Simple DA ~ Indiv. Score Rule < Opinion Pool ~ Market Scoring Rule

Log Rule is Modular p(A|B) $1 if B • Consider bet: $1 if A&B • Changes p(A|B); only log rule keeps p(B) • Also keeps p(C|A&B), p(C| B), I(A, B, C ), I(B, A, C ), I(C, A, B ), I(C, B, A ) – A is var, one of whose values is A, etc. – I(A, B, C ) iff p(A|B&C) = p(A|B) for all values • Log rule uniquely keeps changes modular

No Cost For Combos! • Total cost: C = si true(pfinal) - si true(pinitial) • Expected cost: Ep[C] i i (si(1 i) - si(p)) • For log MSR: = S(p) = - i i log( i) – Let state i = combination of base var values vi – S(pall) var S(pvar), for pvar = { var value v}v – So compared to cost of log rule for each var, all var/value combos cost no more!

How Compute? • Simple: – – Can integrate book orders store 2 N probs, asset values A D C F B • Feasible: overlapping var patches G E H – With simple MSR per patch, is Markov field – Allow trade only if all vars in same patch • How pick/change patch structure? • Arbitrage to make patches agree?

Arbitrage Is Not Modular A A B 1. 2. 3. 4. C E H D F G H Everyone agrees on prices Expert on A gets new info, trades Arbitrage updates all prices Expert on H has no new info, but must trade to restore old info!

Bayesian/Markov Networks • Local info trades not require distant corrections if updates follow Bayes’ rule • Bayesian/Markov net tech does this – Off the shelf exact tech if net forms a tree – Many approx. techs made for non-trees • Some development needed – Must update user assets as well as prices – Need robust to gaming on errors – stochastic?

Summary • How elicit informed estimates? – Scoring rules if N/Q 1, info/predict markets if 1 • Market scoring rules do both: – Key insight … reused scoring rules are market makers – Browse billions of estimates, change ones want via bets – Lab tests confirm ability; are growing # groups using • Log rule has many advantages – If bet on p(A|B), keeps p(B), I(A, B, C ), I(B, A, C ) … – Noisy choices easier to interpret – Costs no more for all var/value combos – Computation simplified, but still issues to explore