Модуль и его приложения Содержание Понятие модуля

Модуль и его приложения

Содержание: Понятие модуля Свойства модуля 1°– 5° Свойства модуля 6°– 10° Геометрическая интерпретация модуля Примеры Решение уравнений вида | f(x)|= a Решение уравнений вида | f(x)|= g(x) Решение уравнений вида |f(x)| = |g(x)|

Понятие модуля Абсолютной величиной (модулем) действительного числа а называется само число а, если оно неотрицательное, и число, противоположное а, если а – отрицательное. |а|= а, если а ≥ 0 – а, если а < 0

Свойства модуля 1° |а|=|– а| 2° |а ∙ b|=|а|∙|b| a |a| 3° = |b| , где b ≠ 0 b 4° |а + b|=|а|+|b| если а≥ 0 иb≥ 0 5° |а|+|b|= а + b если а≥ 0 иb≥ 0

Свойства модуля 6° |а – b|=|а|+|b| если а∙b ≤ 0 7° |а|2 = а 2 8° |а|–|b|≥ 0 если а 2 – b 2 ≥ 0 9° √а 2 = |а| 10° |а 1 + a 2 +…+ an|≤ |а 1|+|a 2|+ +…+|an|

Геометрическая интерпретация модуля |а| |-а| -а 0 а х Это расстояние от начала отсчета до точки, изображающей число.

Примеры Раскрыть модули: 1) 2) 3) 6) 7) 8) 4) 5) 9)

Решение уравнений вида |f(x)|= a f(x) = – a Пример: |x – 8|= 5 x– 8=– 5 ⇔ x = 13 x=3 Ответ: 3; 13.

Решите уравнения вида |f(x)|= a |2 x – 3|= 4 |5 x + 6|= 7 |9 – 3 x |= 6 |4 x + 2|= – 1 |8 – 2 x|= 0 |10 x + 3|= 16 |24 – 3 x|= 12 |2 x + 30|= 48 x 1 = 3, 5; x 1 = 0, 2; x 1 = 1; x Ø x=4 x 1 = 1, 3; x 1 = 12; x 1 = 9; x 2 = – 0, 5 x 2 = – 2, 6 x 2 = 5 x 2 = – 1, 9 x 2 = 4 x 2 = – 39

Решение уравнений вида |f(x)|= g(x) f(х) = g(х) ≥ 0 f(х) = – g(х) ≥ 0

Пример: |3 х – 10| = х – 2 3 x – 10 = x – 2 x– 2≥ 0 3 x – 10 = 2 – x x– 2≥ 0 ⇔ x=4 x=3 ⇔ 2 x = 8 x≥ 2 4 x = 12 x≥ 2 Ответ: 3; 4. ⇔

Решение уравнений вида |f(x)| = |g(x)| f(х) = g(х) f(х) = – g(х) Пример: |x – 2| = |3 – х| х– 2 =3–х ⇔ х– 2=– 3+х х = 2, 5 2 х = 5 ⇔ х Ø – 2=– 3 Ответ: 2, 5.

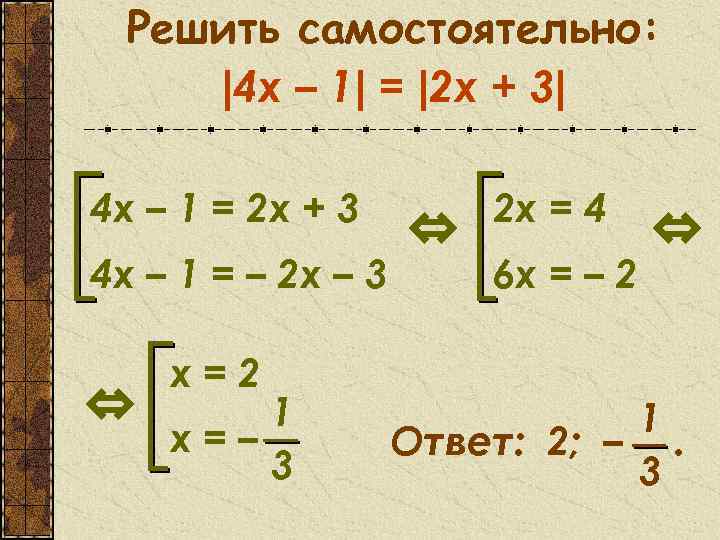Решить самостоятельно: |4 x – 1| = |2 х + 3| 4 х – 1 = 2 x + 3 4 х – 1 = – 2 x – 3 ⇔ х=2 1 х=– 3 ⇔ 2 х = 4 6 x = – 2 ⇔ 1 Ответ: 2; –. 3

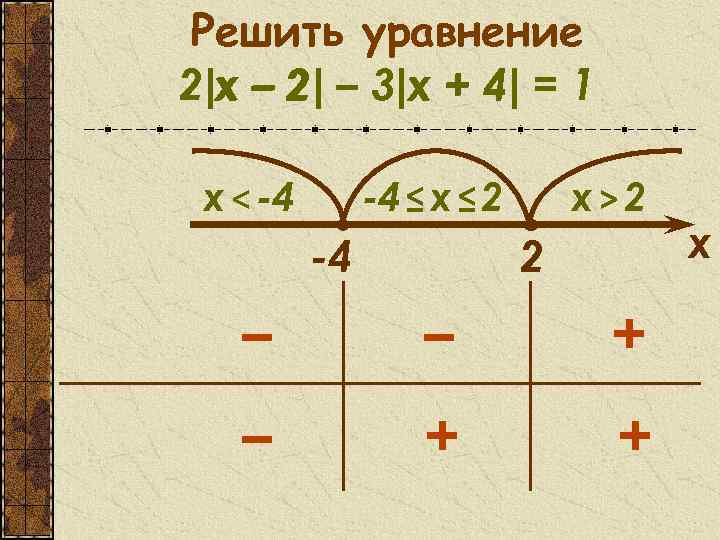Решить уравнение 2|x – 2 – 3|х + 4 = 1 x 2| x 4| x < -4 -4 ≤ x ≤ 2 -4 x>2 2 – – + + х

Решить уравнение 2|x – 2| – 3|х + 4| = 1 x<– 4 2(– x + 2) – 3(– x – 4) =1 x<– 4 – 4≤x≤ 2 2(– x + 2) – 3(x + 4) =1 – 4≤x≤ 2 x = – 15 ⇔ x = – 1, 8 x>2 2(x – 2) – 3(x + 4) =1 x = – 17 Ответ: – 15; – 1, 8.

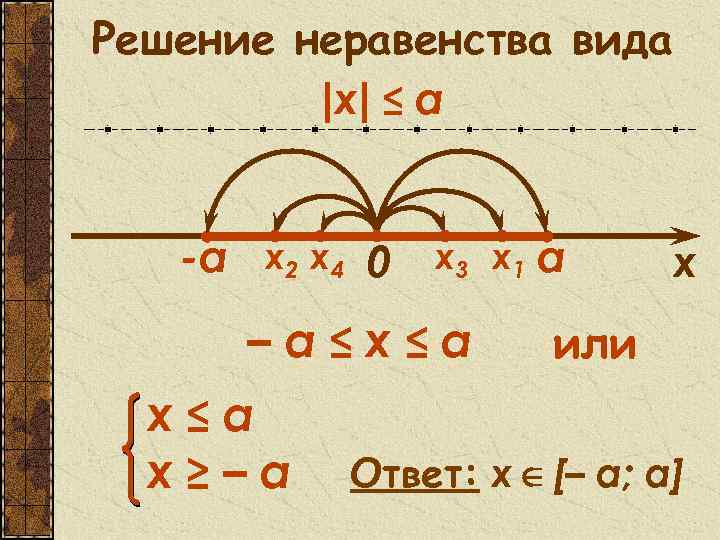Решение неравенства вида |x| ≤ а -а х2 х4 0 х3 х1 а –а≤x≤а х≥–а х или Ответ: x [– а; a]

Решение неравенства вида |f(x)| ≤ а – а ≤ f(x) ≤ а Пример: |x – 5| ≤ 7 – 7≤x– 5≤ 7 +5 – 7+5≤x– 5+5≤ 7+5 – 2 ≤ x ≤ 12 Ответ: [ – 2; 12]

Решите самостоятельно: |5 x + 8| < 12 – 12 < 5 x + 8 < 12 – 8 – 12 – 8 < 5 x + 8 – 8 < 12 – 8 – 20 < 5 x < 4 : 5 – 20 : 5 < 5 x : 5 < 4 : 5 – 4 < x < 0, 8 Ответ: (– 4; 0, 8)

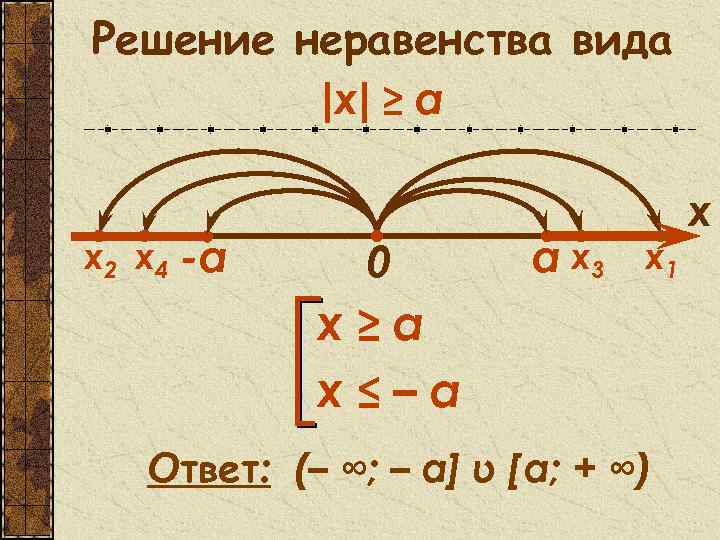Решение неравенства вида |x| ≥ а х2 х4 -а 0 а х3 х1 х≥а х≤–а Ответ: (– ∞; – a] υ [ a; + ∞) х

Решение неравенства вида |f(x)| ≥ а f(x) ≤ – а |x + 4| ≥ 6 x+4≥ 6 x≥ 2 ⇔ x ≤ – 10 x+4≤– 6 Пример: Ответ: (– ∞; – 10] U [ 2; + ∞)

Решите самостоятельно: |10 x – 7 | > 19 10 x – 7 < – 19 ⇔ ⇔ 10 x > 26 10 x < – 12 x > 2, 6 x < – 1, 2 Ответ: (– ∞; – 1, 2) U (2, 6; + ∞) ⇔

Примеры |2 x + 8|–|x – 5|= 12 |x 2 + 3 x|= 2(x + 1) |x – 6|=|x 2 – 5 x + 9|

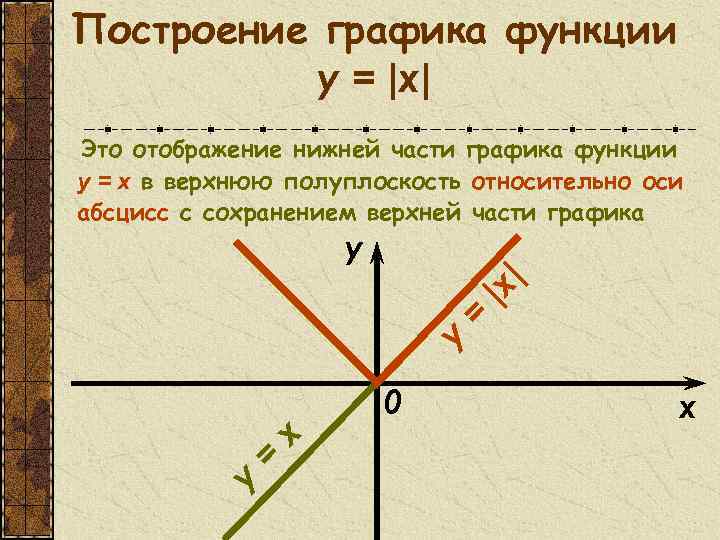Построение графика функции y = |x| Это отображение нижней части графика функции y = x в верхнюю полуплоскость относительно оси абсцисс с сохранением верхней части графика y = |x | y y = x 0 x

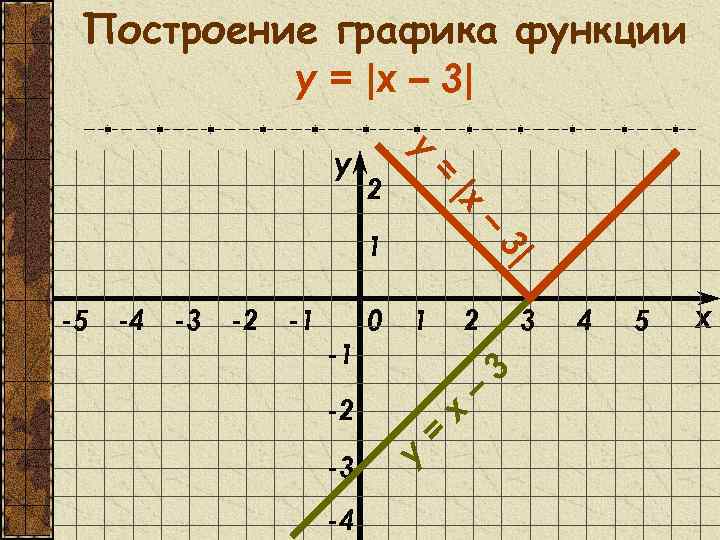Построение графика функции y = |x – 3| y = y |x 2 – -1 -2 0 1 2 3 -1 – -2 x -3 = -4 -3 -4 y -5 3| 1 3 4 5 x

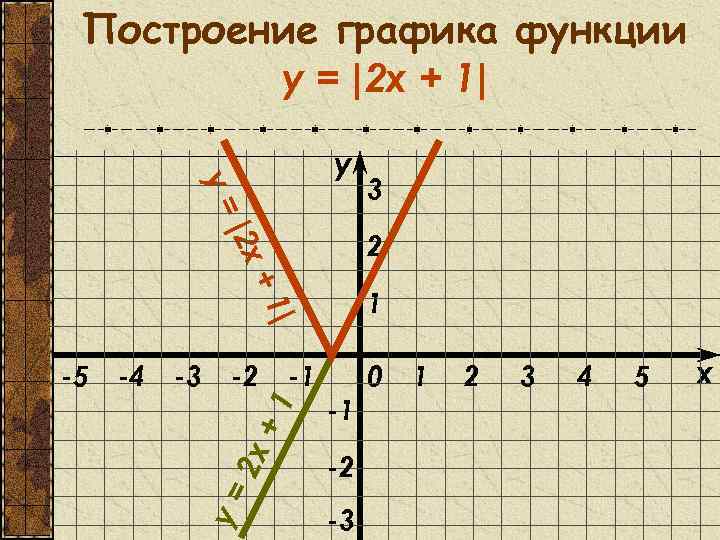Построение графика функции y = |2 x + 1| y= y | 2 x 2 +1 1 | -2 -1 +1 -3 2 x -4 y= -5 3 -1 -2 -3 0 1 2 3 4 5 x

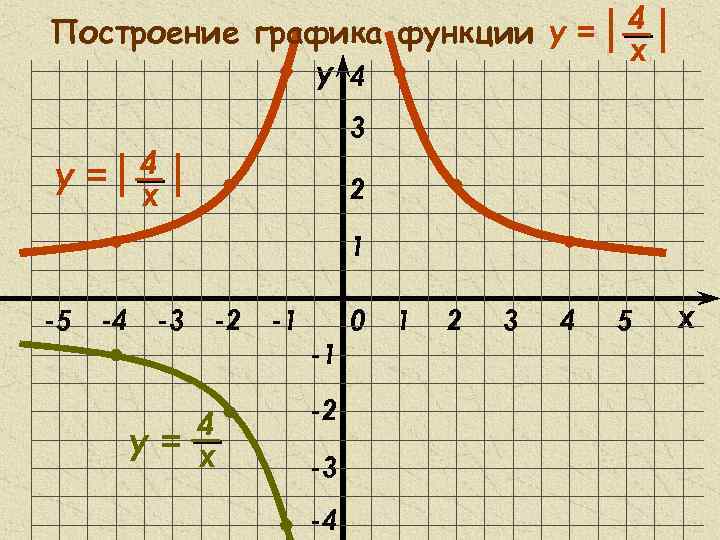Построение графика функции y = | 4 х y 4 | 3 y =| 4 | 2 х 1 -5 -4 -3 -2 4 y= х -1 -1 -2 -3 -4 0 1 2 3 4 5 x

Построение графика функции y = |x + 2| – |x – 3| x < -2 -2 ≤ x ≤ 3 -2 x>3 x 3 x+2 – + + x– 3 – – +

Построение графика функции y = |x + 2| – |x – 3| x<– 2 у=–x– 2+x– 3 x<– 2 – 2≤x≤ 3 у=x+2+x– 3 – 2≤x≤ 3 у=– 5 ⇔ у = 2 х – 1 x>3 у=x+2–x+3 у=5

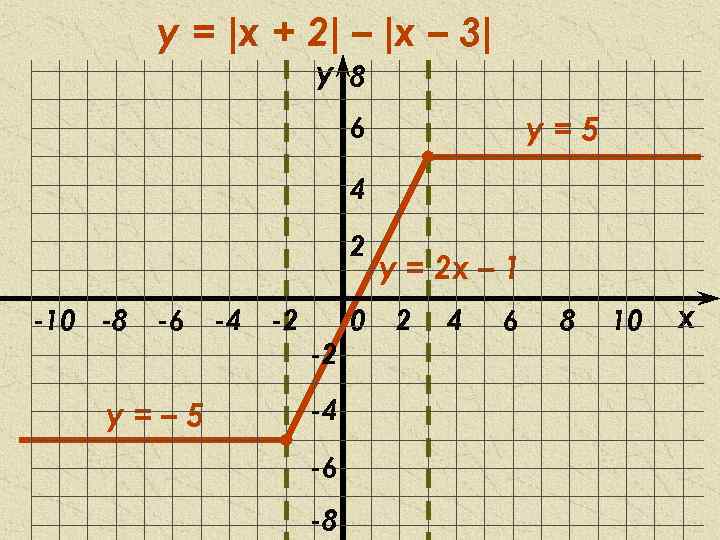y = |x + 2| – |x – 3| y 8 у=5 6 4 2 -10 -8 -6 у=– 5 -4 -2 -2 -4 -6 -8 0 у = 2 х – 1 2 4 6 8 10 x

Построение графика функции y = |x + 1| + |x – 4| x < -1 -1 ≤ x ≤ 4 -1 x> 4 x+1 – + + x– 4 – – +

Построение графика функции y = |x + 1| + |x – 4| x<– 1 у=–x– 1–x+4 x<– 1 – 1≤x≤ 4 у=x+1–x+4 – 1≤x≤ 4 у = – 2 х + 3 ⇔ у=5 x>4 у=x+1+x– 4 у = 2 х – 3

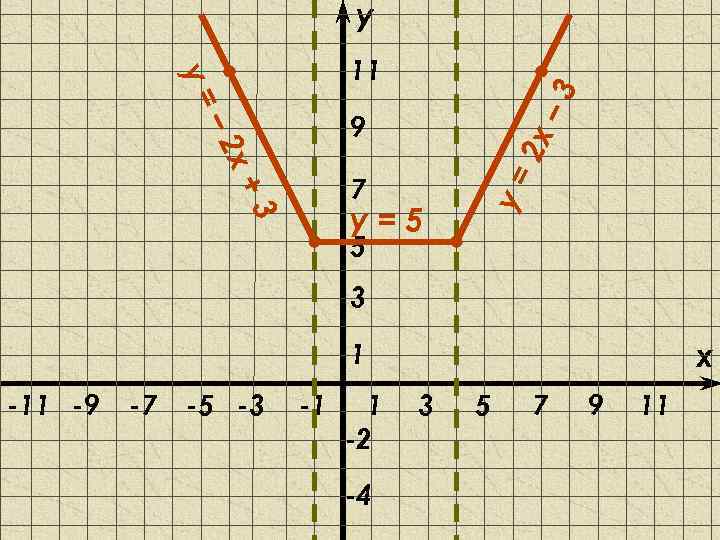y 3 у= 11 2 х – 7 3 у=5 у= х+ – 2 9 5 3 x 1 -11 -9 -7 -5 -3 -1 1 -2 -4 3 5 7 9 11