Модуль 2 Размерные эффекты в
































![Магнитное поле в присутствии вещества Напряженность МП H [A/m] Магнитное поле в присутствии вещества Напряженность МП H [A/m]](https://present5.com/presentation/3/176394115_349362760.pdf-img/176394115_349362760.pdf-49.jpg)















 Модуль 2 Размерные эффекты в наноструктурах
Модуль 2 Размерные эффекты в наноструктурах
 Традиционная цепочка (триада) • Химический состав • Атомно-молекулярная структура • Физико-химические свойства
Традиционная цепочка (триада) • Химический состав • Атомно-молекулярная структура • Физико-химические свойства
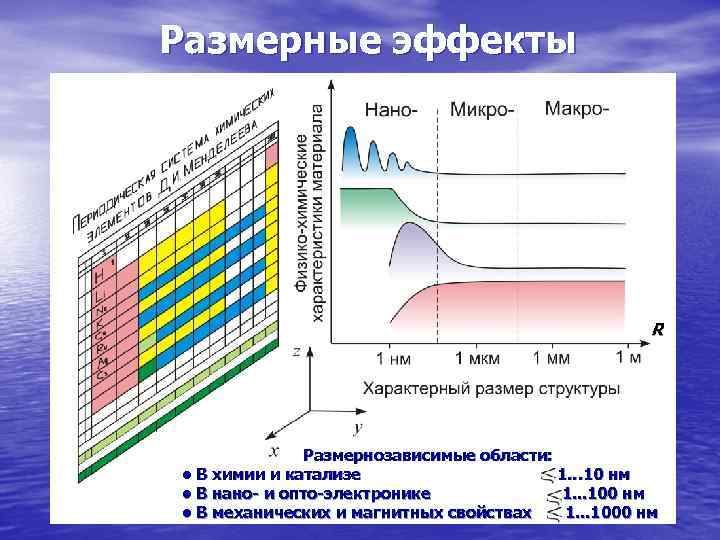
 Размерные эффекты R Размернозависимые области: • В химии и катализе 1… 10 нм • В нано- и опто-электронике 1. . . 100 нм • В механических и магнитных свойствах 1. . . 1000 нм
Размерные эффекты R Размернозависимые области: • В химии и катализе 1… 10 нм • В нано- и опто-электронике 1. . . 100 нм • В механических и магнитных свойствах 1. . . 1000 нм
 Размерные эффекты (РЭ) – значительные изменения физико- химических характеристик объекта при неизменном химическом составе в результате варьирования: • его внешних размеров • размеров морфологических size effects или структурных единиц • формы и размерности dimension effects В области малых размеров они могут иметь весьма разнообразную природу и приводить к сильным изменениям всех физико-химических свойств вещества без изменения его состава. Эти изменения могут носить различный характер и происходить для разных свойств в различных интервалах характерных размеров (даже для одного и того же вещества). Именно поэтому невозможно указать точно границы нанообласти без дополнительных уточнений. Образно говоря, свойства веществ (даже одноэлементных) зависят не только от положения элементов в периодической таблице Д. И. Менделеева, но и характерных размеров образца, т. е. R может играть роль третьей координаты в ней.
Размерные эффекты (РЭ) – значительные изменения физико- химических характеристик объекта при неизменном химическом составе в результате варьирования: • его внешних размеров • размеров морфологических size effects или структурных единиц • формы и размерности dimension effects В области малых размеров они могут иметь весьма разнообразную природу и приводить к сильным изменениям всех физико-химических свойств вещества без изменения его состава. Эти изменения могут носить различный характер и происходить для разных свойств в различных интервалах характерных размеров (даже для одного и того же вещества). Именно поэтому невозможно указать точно границы нанообласти без дополнительных уточнений. Образно говоря, свойства веществ (даже одноэлементных) зависят не только от положения элементов в периодической таблице Д. И. Менделеева, но и характерных размеров образца, т. е. R может играть роль третьей координаты в ней.
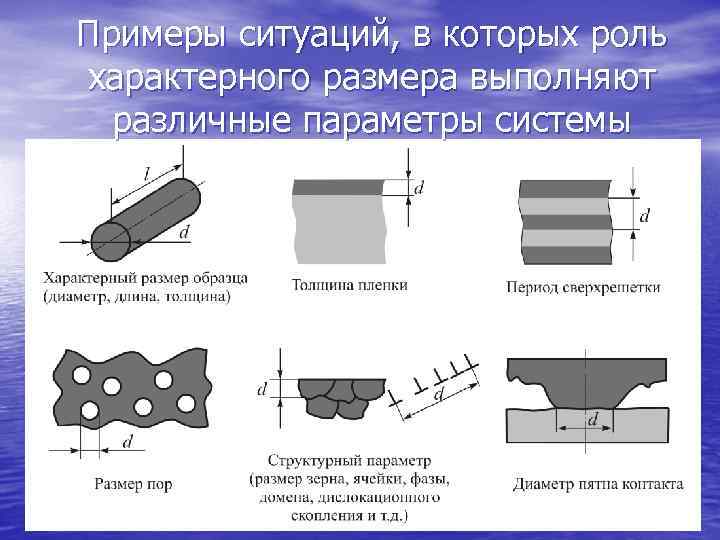
 Примеры ситуаций, в которых роль характерного размера выполняют различные параметры системы
Примеры ситуаций, в которых роль характерного размера выполняют различные параметры системы
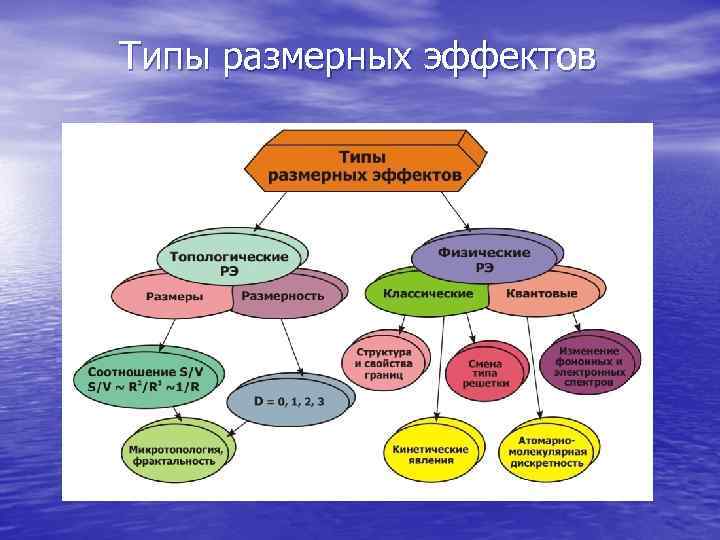
 Типы размерных эффектов
Типы размерных эффектов
 Типы размерных эффектов • РЭ можно классифицировать различным образом, принимая во внимание разные признаки. Так, на слайде показано деление на «геометрические» и «физические» РЭ. Последние могут иметь классическую или квантовую природу/объяснение и возникать из-за того, что при уменьшении размеров объекта они начинают приближаться (сравниваться) с длинами свободного пробега носителей или волн Де Бройля, корреляционными радиусами, критическими размерами зародыша новой фазы или домена, размерами атомов/молекул и т. п. • Так или иначе, возникновение РЭ приводит к тому, что интенсивные характеристики вещества (плотность, электро- и теплопроводность, коэффициент диффузии и др. ), которые не зависят от размеров или объема объекта в макрошкале, переходят в разряд экстенсивных, т. е. зависящих от размера системы и перестают совпадать с макроскопическими.
Типы размерных эффектов • РЭ можно классифицировать различным образом, принимая во внимание разные признаки. Так, на слайде показано деление на «геометрические» и «физические» РЭ. Последние могут иметь классическую или квантовую природу/объяснение и возникать из-за того, что при уменьшении размеров объекта они начинают приближаться (сравниваться) с длинами свободного пробега носителей или волн Де Бройля, корреляционными радиусами, критическими размерами зародыша новой фазы или домена, размерами атомов/молекул и т. п. • Так или иначе, возникновение РЭ приводит к тому, что интенсивные характеристики вещества (плотность, электро- и теплопроводность, коэффициент диффузии и др. ), которые не зависят от размеров или объема объекта в макрошкале, переходят в разряд экстенсивных, т. е. зависящих от размера системы и перестают совпадать с макроскопическими.
 Конституционные и революционные РЭ • Условно все РЭ можно разбить на два класса по признаку следования определенным скейлинговым соотношениям, согласующимся с некоторой моделью явления (эволюционные или конституционные РЭ), или, напротив, резкого отклонения от этого следования, т. е. аномального, не укладывающегося в данную модель поведения (революционные РЭ), при уменьшении характерных размеров системы ниже критических. • Примерами первых может служить монотонный рост лапласовского давления, отношения площади поверхности наночастиц (НЧ) к их объему (и соответствующее увеличение роли приповерхностных состояний и процессов) при уменьшении размеров НЧ, а вторых – проявления атомно- молекулярной дискретности, возникновение размерного (вторичного) квантования, квантового туннелирования, баллистического режима переноса при уменьшении наименьшего размера НЧ ниже некоторого критического.
Конституционные и революционные РЭ • Условно все РЭ можно разбить на два класса по признаку следования определенным скейлинговым соотношениям, согласующимся с некоторой моделью явления (эволюционные или конституционные РЭ), или, напротив, резкого отклонения от этого следования, т. е. аномального, не укладывающегося в данную модель поведения (революционные РЭ), при уменьшении характерных размеров системы ниже критических. • Примерами первых может служить монотонный рост лапласовского давления, отношения площади поверхности наночастиц (НЧ) к их объему (и соответствующее увеличение роли приповерхностных состояний и процессов) при уменьшении размеров НЧ, а вторых – проявления атомно- молекулярной дискретности, возникновение размерного (вторичного) квантования, квантового туннелирования, баллистического режима переноса при уменьшении наименьшего размера НЧ ниже некоторого критического.
 Причины РЭ (классическое приближение) БОЛЬШАЯ ДОЛЯ ПРИПОВЕРХНОСТНЫХ ИЛИ ЗЕРНОГРАНИЧНЫХ АТОМОВ ПО ОТНОШЕНИЮ К ОБЪЕМНЫМ НИЗКИЕ КООРДИНАТНЫЕ ЧИСЛА АТОМОВ НА ПОВЕРХНОСТИ, В УГЛАХ СТУПЕНЕК, УСТУПОВ, МАГИЧЕСКИЕ ЧИСЛА И Т. Д. ОЧИСТКА ОБЪЕМА ОТ ДЕФЕКТОВ СИЛАМИ ИЗОБРАЖЕНИЯ, ЛИНЕЙНОГО И ПОВЕРХНОСТНОГО НАПРЯДЕНИЯ РАЗМЕРНЫЕ ЭФФЕКТЫ, ОБУСЛОВЛЕННЫЕ РАССЕЯНИЕМ, РЕКОМБИНАЦИЕЙ И ОТРАЖЕНИЕМ НА ГРАНИЦАХ, БАЛЛИСТИЧЕСКИЙ РЕЖИМ ХАРАКТЕРНЫЙ РАЗМЕР НАНОЧАСТИЦЫ R СОПОСТАВИМ ИЛИ МЕНЬШЕ КРИТИЧЕСКОГО РАЗМЕРА ЗАРОДЫША Rn НОВОЙ ФАЗЫ, ДОМЕНА, ДИСЛОКАЦИОННОЙ ПЕТЛИ И Т. П.
Причины РЭ (классическое приближение) БОЛЬШАЯ ДОЛЯ ПРИПОВЕРХНОСТНЫХ ИЛИ ЗЕРНОГРАНИЧНЫХ АТОМОВ ПО ОТНОШЕНИЮ К ОБЪЕМНЫМ НИЗКИЕ КООРДИНАТНЫЕ ЧИСЛА АТОМОВ НА ПОВЕРХНОСТИ, В УГЛАХ СТУПЕНЕК, УСТУПОВ, МАГИЧЕСКИЕ ЧИСЛА И Т. Д. ОЧИСТКА ОБЪЕМА ОТ ДЕФЕКТОВ СИЛАМИ ИЗОБРАЖЕНИЯ, ЛИНЕЙНОГО И ПОВЕРХНОСТНОГО НАПРЯДЕНИЯ РАЗМЕРНЫЕ ЭФФЕКТЫ, ОБУСЛОВЛЕННЫЕ РАССЕЯНИЕМ, РЕКОМБИНАЦИЕЙ И ОТРАЖЕНИЕМ НА ГРАНИЦАХ, БАЛЛИСТИЧЕСКИЙ РЕЖИМ ХАРАКТЕРНЫЙ РАЗМЕР НАНОЧАСТИЦЫ R СОПОСТАВИМ ИЛИ МЕНЬШЕ КРИТИЧЕСКОГО РАЗМЕРА ЗАРОДЫША Rn НОВОЙ ФАЗЫ, ДОМЕНА, ДИСЛОКАЦИОННОЙ ПЕТЛИ И Т. П.
 Причины РЭ квантовой природы • Изменение электронных и фононных спектров; • Туннелирование; • Изменение роли обменного взаимодействия; • Приповерхностные состояния • «Обеднение» статистики ввиду уменьшения числа атомов в системе.
Причины РЭ квантовой природы • Изменение электронных и фононных спектров; • Туннелирование; • Изменение роли обменного взаимодействия; • Приповерхностные состояния • «Обеднение» статистики ввиду уменьшения числа атомов в системе.
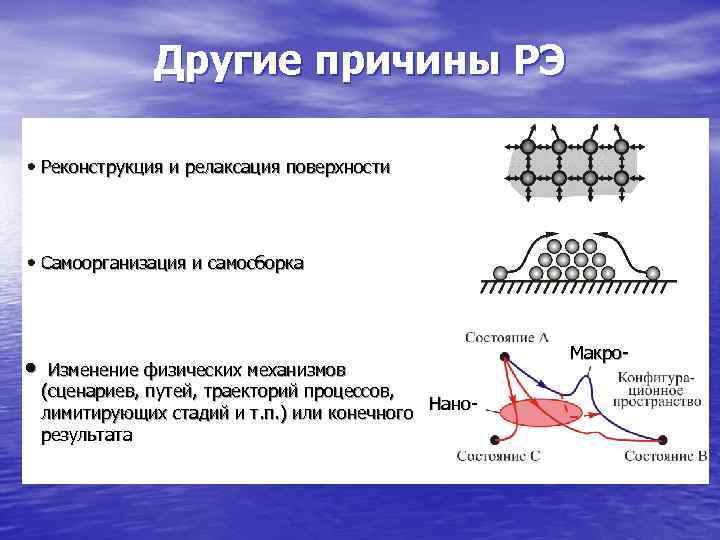
 Другие причины РЭ Реконструкция и релаксация поверхности Самоорганизация и самосборка Макро- • Изменение физических механизмов (сценариев, путей, траекторий процессов, Нано- лимитирующих стадий и т. п. ) или конечного результата
Другие причины РЭ Реконструкция и релаксация поверхности Самоорганизация и самосборка Макро- • Изменение физических механизмов (сценариев, путей, траекторий процессов, Нано- лимитирующих стадий и т. п. ) или конечного результата
 Физическая наномеханика • Динамика наночастиц и наносистем • Нанофлюидика • Пластичность и прочность материалов • Нанотрибология
Физическая наномеханика • Динамика наночастиц и наносистем • Нанофлюидика • Пластичность и прочность материалов • Нанотрибология
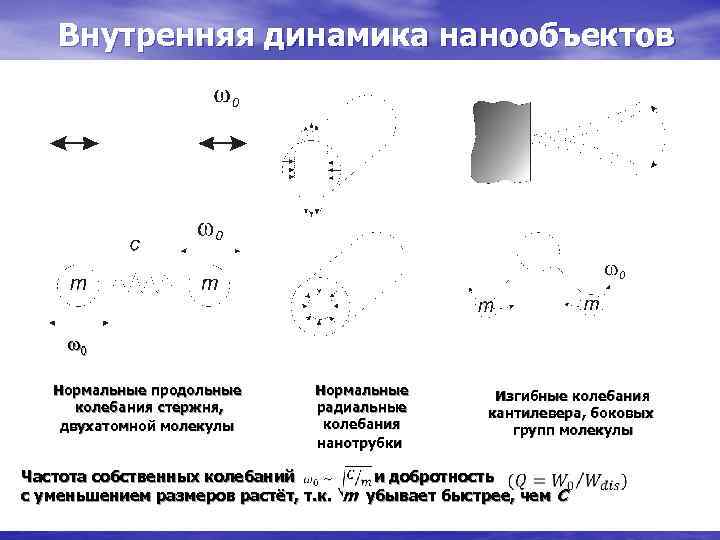
 Внутренняя динамика нанообъектов 0 Нормальные продольные Нормальные Изгибные колебания стержня, радиальные кантилевера, боковых двухатомной молекулы колебания групп молекулы нанотрубки Частота собственных колебаний и добротность с уменьшением размеров растёт, т. к. m убывает быстрее, чем С
Внутренняя динамика нанообъектов 0 Нормальные продольные Нормальные Изгибные колебания стержня, радиальные кантилевера, боковых двухатомной молекулы колебания групп молекулы нанотрубки Частота собственных колебаний и добротность с уменьшением размеров растёт, т. к. m убывает быстрее, чем С
 Особенности механического поведения нанообъектов При уменьшении размеров деталей, компонентов гибридных устройств, отдельных частиц происходит следующее: § Растет частота их собственных колебаний, а следовательно, возможное быстродействие устройства. Так, при соблюдении геометрического подобия в стержнеобразном объекте длиной L и поперечным сечением S, в котором возбуждаются колебания типа осевого растяжения-сжатия, собственная частота 0 зависит от L как . В условиях геометрического подобия для консольной балочки прямоугольного сечения длиной L, шириной b и толщиной h (их широко используют в атомно- силовой микроскопии, сенсорах, актуаторах) . В устройствах нанометровых размеров 0 109 -1011 с-1, а молекулярных – 0 ~ 1012… 1014 с-1. § Роль поверхностных сил (трения, адгезии, капиллярных, кулоновских) и их вклад в динамику растут по отношению к объемным (гравитационным, магнитным, инерционным) как L-1, поскольку S/V ~ L-1. При L 100 нм механическое поведение наночастиц целиком зависит от поверхностных сил. § Роль термических флуктуаций нарастает.
Особенности механического поведения нанообъектов При уменьшении размеров деталей, компонентов гибридных устройств, отдельных частиц происходит следующее: § Растет частота их собственных колебаний, а следовательно, возможное быстродействие устройства. Так, при соблюдении геометрического подобия в стержнеобразном объекте длиной L и поперечным сечением S, в котором возбуждаются колебания типа осевого растяжения-сжатия, собственная частота 0 зависит от L как . В условиях геометрического подобия для консольной балочки прямоугольного сечения длиной L, шириной b и толщиной h (их широко используют в атомно- силовой микроскопии, сенсорах, актуаторах) . В устройствах нанометровых размеров 0 109 -1011 с-1, а молекулярных – 0 ~ 1012… 1014 с-1. § Роль поверхностных сил (трения, адгезии, капиллярных, кулоновских) и их вклад в динамику растут по отношению к объемным (гравитационным, магнитным, инерционным) как L-1, поскольку S/V ~ L-1. При L 100 нм механическое поведение наночастиц целиком зависит от поверхностных сил. § Роль термических флуктуаций нарастает.
 Схематическое изображение зависимости механических характеристик твердых тел от определяющего размера объекта I – плохо исследованная область с R*≤ 10 нм; I +II – наномасштабная область; III – микромасштабная область действия закона Холла – Петча; IV – область проявления статистических масштабных эффектов, согласующаяся с теорией Вейбулла; E – модуль Юнга; s и t - нормальные и сдвиговые напряжения соответственно.
Схематическое изображение зависимости механических характеристик твердых тел от определяющего размера объекта I – плохо исследованная область с R*≤ 10 нм; I +II – наномасштабная область; III – микромасштабная область действия закона Холла – Петча; IV – область проявления статистических масштабных эффектов, согласующаяся с теорией Вейбулла; E – модуль Юнга; s и t - нормальные и сдвиговые напряжения соответственно.
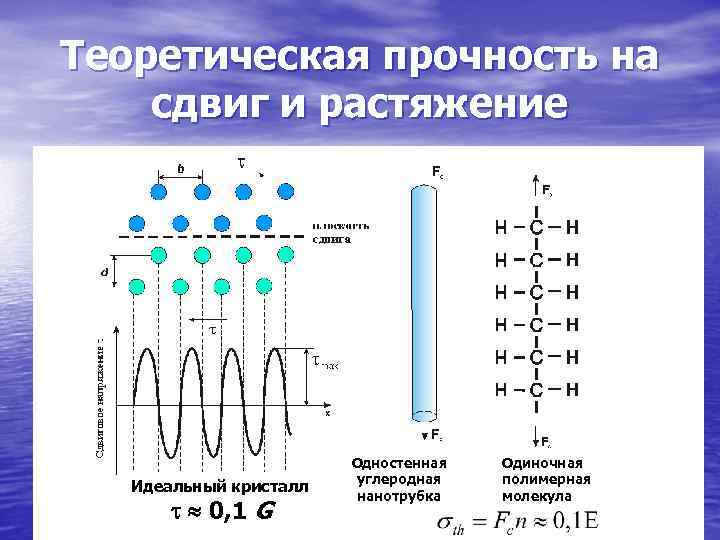
 Теоретическая прочность на сдвиг и растяжение Одностенная Одиночная углеродная полимерная Идеальный кристалл нанотрубка молекула 0, 1 G
Теоретическая прочность на сдвиг и растяжение Одностенная Одиночная углеродная полимерная Идеальный кристалл нанотрубка молекула 0, 1 G
 Прочность в наношкале Прочность кристаллической решетки на разрыв и на сдвиг определяется в первую очередь силами связи атомов в решетке. (Необратимый сдвиг приводит к пластическому течению, искажающему форму детали, что в большинстве случаев делает её непригодной к дальнейшей эксплуатации. Поэтому такую ситуацию и определяют как прочность на сдвиг). Предельные напряжения, которые вызывают потерю упругой устойчивости идеальной (бездефектной) кристаллической решетки называют теоретическим пределом прочности на растяжение th и сдвиг th при действии нормальных и касательных напряжений соответственно. Дадим простейшую оценку этих величин в рамках классической модели твердого тела. Положим, что межатомные силы при сдвиге одной кристаллической плоскости относительно другой меняются по гармоническому закону: (х)= max Sin(2 x/b). Для малых смещений x действует закон Гука (х)= Gx/d (G – модуль сдвига, d – расстояние между соседними плоскостями) и Sinx x. Тогда (при b d). Впервые такую оценку сделал Я. И. Френкель в 20 - е годы прошлого века. Другие, более строгие модели (в том числе и квантовые) также дают th 0, 1 G. Аналогично для растягивающих напряжений th 0, 1 Е (где Е – модуль th Юнга). Значения th и th превышают прочность реальных конструкционных материалов от 10 до 1000 раз, что говорит о наличии большого резерва упрочнения. Одним из перспективных способов является уменьшение структурных единиц материала (зерен, фаз, доменов) или самих изделий до нанометровых размеров. Их прочность приближается к теоретическим пределам за счет уменьшения числа и мощности присутствующих структурных дефектов, резко понижающих прочность традиционных материалов (более подробно см. Модуль 8).
Прочность в наношкале Прочность кристаллической решетки на разрыв и на сдвиг определяется в первую очередь силами связи атомов в решетке. (Необратимый сдвиг приводит к пластическому течению, искажающему форму детали, что в большинстве случаев делает её непригодной к дальнейшей эксплуатации. Поэтому такую ситуацию и определяют как прочность на сдвиг). Предельные напряжения, которые вызывают потерю упругой устойчивости идеальной (бездефектной) кристаллической решетки называют теоретическим пределом прочности на растяжение th и сдвиг th при действии нормальных и касательных напряжений соответственно. Дадим простейшую оценку этих величин в рамках классической модели твердого тела. Положим, что межатомные силы при сдвиге одной кристаллической плоскости относительно другой меняются по гармоническому закону: (х)= max Sin(2 x/b). Для малых смещений x действует закон Гука (х)= Gx/d (G – модуль сдвига, d – расстояние между соседними плоскостями) и Sinx x. Тогда (при b d). Впервые такую оценку сделал Я. И. Френкель в 20 - е годы прошлого века. Другие, более строгие модели (в том числе и квантовые) также дают th 0, 1 G. Аналогично для растягивающих напряжений th 0, 1 Е (где Е – модуль th Юнга). Значения th и th превышают прочность реальных конструкционных материалов от 10 до 1000 раз, что говорит о наличии большого резерва упрочнения. Одним из перспективных способов является уменьшение структурных единиц материала (зерен, фаз, доменов) или самих изделий до нанометровых размеров. Их прочность приближается к теоретическим пределам за счет уменьшения числа и мощности присутствующих структурных дефектов, резко понижающих прочность традиционных материалов (более подробно см. Модуль 8).
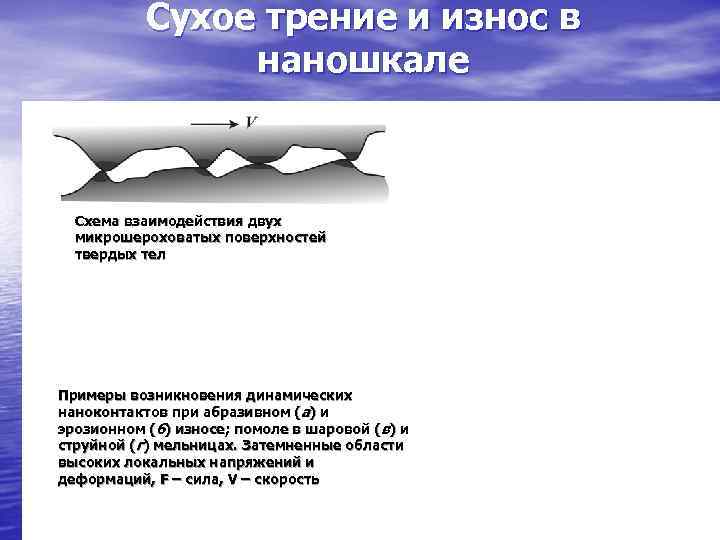
 Сухое трение и износ в наношкале Схема взаимодействия двух микрошероховатых поверхностей твердых тел Примеры возникновения динамических наноконтактов при абразивном (а) и эрозионном (б) износе; помоле в шаровой (в) и струйной (г) мельницах. Затемненные области высоких локальных напряжений и деформаций, F – сила, V – скорость
Сухое трение и износ в наношкале Схема взаимодействия двух микрошероховатых поверхностей твердых тел Примеры возникновения динамических наноконтактов при абразивном (а) и эрозионном (б) износе; помоле в шаровой (в) и струйной (г) мельницах. Затемненные области высоких локальных напряжений и деформаций, F – сила, V – скорость
 Сухое трение, абразивный и эрозионный износ имеют колоссальное значение для практики. Они происходят не по всей видимой контактирующей поверхности, а на микро-, субмикро- и нановыступах (обычное соотношение реальной площади контакта с кажущейся может составлять 0, 1 – 0, 001). Наноконтакты – это типичные нанообъеткы, свойства материала в которых существенно отличаются от объемных макроскопических. Так, предел текучести, твердость, хрупкость, вязкость разрушения в них могут во много раз отличаться от табличных макроскопических. Следует также учесть, что трение и износ – не есть чисто механические процессы. Большую роль в их механизмах играют физико-химические процессы в контактных пятнах, адгезионные, тепловые и электромагнитные явления. В неподвижных и скользящих наноконтактах возникают сложные электронные процессы, зачастую с проявлением размерного квантования. Весь этот комплекс наноконтактных процессов изучает недавно начавшая формироваться наука – нанотрибология. Её основная задача – вывести известные феноменологические законы трения и износа из «первых принципов» , т. е. фундаментальных принципов физики.
Сухое трение, абразивный и эрозионный износ имеют колоссальное значение для практики. Они происходят не по всей видимой контактирующей поверхности, а на микро-, субмикро- и нановыступах (обычное соотношение реальной площади контакта с кажущейся может составлять 0, 1 – 0, 001). Наноконтакты – это типичные нанообъеткы, свойства материала в которых существенно отличаются от объемных макроскопических. Так, предел текучести, твердость, хрупкость, вязкость разрушения в них могут во много раз отличаться от табличных макроскопических. Следует также учесть, что трение и износ – не есть чисто механические процессы. Большую роль в их механизмах играют физико-химические процессы в контактных пятнах, адгезионные, тепловые и электромагнитные явления. В неподвижных и скользящих наноконтактах возникают сложные электронные процессы, зачастую с проявлением размерного квантования. Весь этот комплекс наноконтактных процессов изучает недавно начавшая формироваться наука – нанотрибология. Её основная задача – вывести известные феноменологические законы трения и износа из «первых принципов» , т. е. фундаментальных принципов физики.
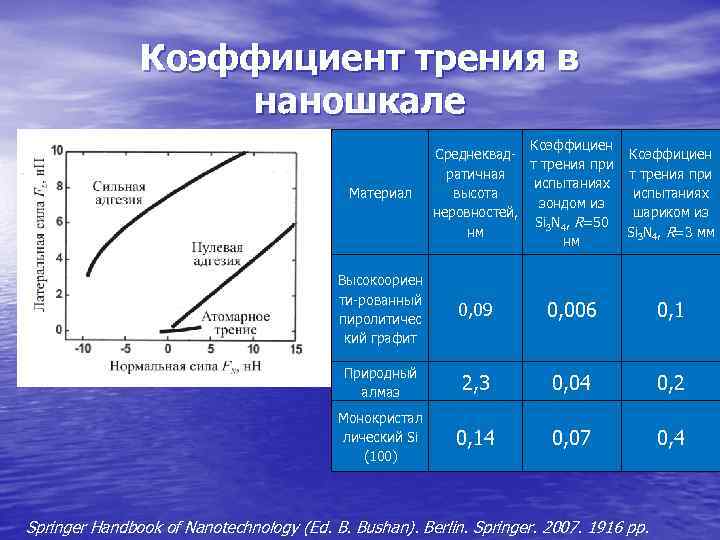
 Коэффициент трения в наношкале Коэффициен Среднеквад- Коэффициен т трения при ратичная т трения при испытаниях Материал высота испытаниях зондом из неровностей, шариком из Si 3 N 4, R=50 нм Si 3 N 4, R=3 мм нм Высокоориен ти-рованный пиролитичес 0, 09 0, 006 0, 1 кий графит Природный алмаз 2, 3 0, 04 0, 2 Монокристал лический Si 0, 14 0, 07 0, 4 (100) Springer Handbook of Nanotechnology (Ed. B. Bushan). Berlin. Springer. 2007. 1916 pp.
Коэффициент трения в наношкале Коэффициен Среднеквад- Коэффициен т трения при ратичная т трения при испытаниях Материал высота испытаниях зондом из неровностей, шариком из Si 3 N 4, R=50 нм Si 3 N 4, R=3 мм нм Высокоориен ти-рованный пиролитичес 0, 09 0, 006 0, 1 кий графит Природный алмаз 2, 3 0, 04 0, 2 Монокристал лический Si 0, 14 0, 07 0, 4 (100) Springer Handbook of Nanotechnology (Ed. B. Bushan). Berlin. Springer. 2007. 1916 pp.
 На слайде показана зависимость силы трения от величины нормальной силы для наноконтакта. Видно, адгезия, добавляющая силу прижатия к приложенной извне, увеличивает трение. Тем не менее, обычно сухое трение в наношкале намного меньше, чем макромасштабное (некоторые примеры даны в таблице).
На слайде показана зависимость силы трения от величины нормальной силы для наноконтакта. Видно, адгезия, добавляющая силу прижатия к приложенной извне, увеличивает трение. Тем не менее, обычно сухое трение в наношкале намного меньше, чем макромасштабное (некоторые примеры даны в таблице).
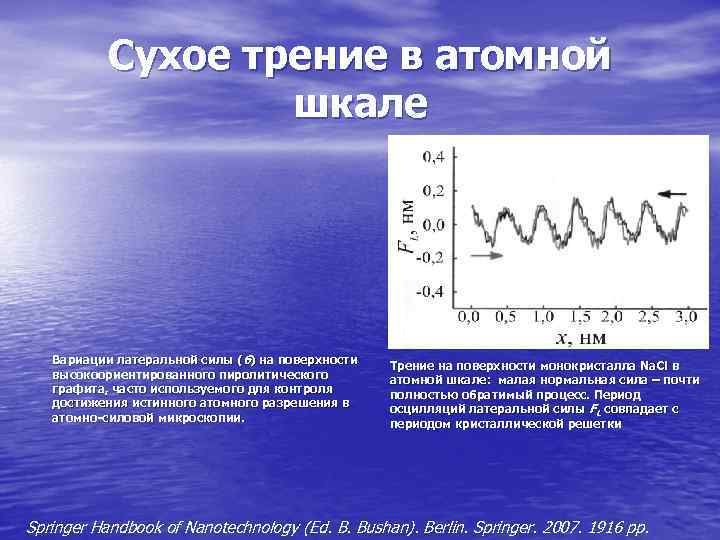
 Сухое трение в атомной шкале Вариации латеральной силы (б) на поверхности Трение на поверхности монокристалла Na. Cl в высокоориентированного пиролитического атомной шкале: малая нормальная сила – почти графита, часто используемого для контроля полностью обратимый процесс. Период достижения истинного атомного разрешения в осцилляций латеральной силы FL совпадает с атомно-силовой микроскопии. периодом кристаллической решетки Springer Handbook of Nanotechnology (Ed. B. Bushan). Berlin. Springer. 2007. 1916 pp.
Сухое трение в атомной шкале Вариации латеральной силы (б) на поверхности Трение на поверхности монокристалла Na. Cl в высокоориентированного пиролитического атомной шкале: малая нормальная сила – почти графита, часто используемого для контроля полностью обратимый процесс. Период достижения истинного атомного разрешения в осцилляций латеральной силы FL совпадает с атомно-силовой микроскопии. периодом кристаллической решетки Springer Handbook of Nanotechnology (Ed. B. Bushan). Berlin. Springer. 2007. 1916 pp.
 Наиболее фундаментальный уровень в изучении любого явления в наномире может быть достигнут при рассмотрении его электронно- спиновом и атомно-молекулярном уровне. На ряде материалов (чистых монокристаллических металлах, ионных и полупроводниковых кристаллах, пиролитическом графите, соединении Mo. S 2 и др. ) достигнуто атомное разрешение в регистрации сил трения при движении иглы атомно-силового микроскопа (см. Модуль 5) в режиме регистрации латеральных сил. Видно, что сила взаимодействия зонда с поверхностью модулируется с периодичностью кристаллической решетки. Для некоторых режимов сканирования можно добиться полной обратимости движения и равенства нулю средней величины силы трения. Основная причина диссипации энергии на атомарном уровне - неравномерность движения отдельных атомов, принадлежащих двум контактирующим поверхностям. При надлежащем выборе кристаллографического направления (обычно с большими индексами Миллера) и малой скорости движения небольшой группы атомов вдоль неподвижной поверхности экспериментально достигается «сверхскольжение» (аналог сверхпроводимости и сверхтекучести жидкого гелия), т. е. скольжение с нулевым трением. При не столь тщательно соблюдаемых условиях можно добиться снижения сухого трения в наномасштабе во много раз по сравнению с макроскопическим
Наиболее фундаментальный уровень в изучении любого явления в наномире может быть достигнут при рассмотрении его электронно- спиновом и атомно-молекулярном уровне. На ряде материалов (чистых монокристаллических металлах, ионных и полупроводниковых кристаллах, пиролитическом графите, соединении Mo. S 2 и др. ) достигнуто атомное разрешение в регистрации сил трения при движении иглы атомно-силового микроскопа (см. Модуль 5) в режиме регистрации латеральных сил. Видно, что сила взаимодействия зонда с поверхностью модулируется с периодичностью кристаллической решетки. Для некоторых режимов сканирования можно добиться полной обратимости движения и равенства нулю средней величины силы трения. Основная причина диссипации энергии на атомарном уровне - неравномерность движения отдельных атомов, принадлежащих двум контактирующим поверхностям. При надлежащем выборе кристаллографического направления (обычно с большими индексами Миллера) и малой скорости движения небольшой группы атомов вдоль неподвижной поверхности экспериментально достигается «сверхскольжение» (аналог сверхпроводимости и сверхтекучести жидкого гелия), т. е. скольжение с нулевым трением. При не столь тщательно соблюдаемых условиях можно добиться снижения сухого трения в наномасштабе во много раз по сравнению с макроскопическим
 Поведение взвесей, суспензий, эмульсий нанообъектов в гравитационном поле М Крупные Средние Мелкие Распределение частицы Больцмана В гравитационном поле U=mgh=V gh Распределение частиц по высоте V( - 0)gh k. T V( - 0)gh<
Поведение взвесей, суспензий, эмульсий нанообъектов в гравитационном поле М Крупные Средние Мелкие Распределение частицы Больцмана В гравитационном поле U=mgh=V gh Распределение частиц по высоте V( - 0)gh k. T V( - 0)gh<
 Рассмотрим ансамбль не взаимодействующих между собой классических частиц массой m (модель идеального газа) в гравитационном поле g =9, 81 м 2/с. Эти частицы обладают в поле потенциальной энергией U=mgh и подчиняется статистике Больцмана, в соответствии с которой распределяются по высоте h (вследствие броуновского движения ) так, что в равновесии установится зависимость их концентрации n от h в виде . Здесь n 0=n при h=0 и учтено, что на частицы объемом V и плотностью в среде с плотностью 0 действует выталкивающая сила Архимеда FA=V 0 g. Для численной оценки рассмотрим конкретную суспензию сферических частиц серебра радиусом R в воде, помещенной в пробирку высотой H=0, 1 м при комнатной температуре (Т≈300 K). Тогда - 0≈ 104 кг/м 3, V = 4/3 R 3 и для частиц с R=5 нм n/n 0≈0, 95, для R=10 нм n/n 0≈0, 37, а для R=20 нм n/n 0≈10 -4. Отсюда следует, что ввиду экспоненциально сильной зависимости n/n 0 от V вблизи R=Rc≈10 нм происходит фактически скачок от равномерного распределения частиц по высоте (при R Rc) к их оседанию на дне сосуда (при R Rc). Частицы более легкие, чем жидкость, например, капельки жира в молоке), будут не оседать, а всплывать. Частицы достаточно большого размера будут оседать (при > 0) или всплывать (при < 0) в жидкости.
Рассмотрим ансамбль не взаимодействующих между собой классических частиц массой m (модель идеального газа) в гравитационном поле g =9, 81 м 2/с. Эти частицы обладают в поле потенциальной энергией U=mgh и подчиняется статистике Больцмана, в соответствии с которой распределяются по высоте h (вследствие броуновского движения ) так, что в равновесии установится зависимость их концентрации n от h в виде . Здесь n 0=n при h=0 и учтено, что на частицы объемом V и плотностью в среде с плотностью 0 действует выталкивающая сила Архимеда FA=V 0 g. Для численной оценки рассмотрим конкретную суспензию сферических частиц серебра радиусом R в воде, помещенной в пробирку высотой H=0, 1 м при комнатной температуре (Т≈300 K). Тогда - 0≈ 104 кг/м 3, V = 4/3 R 3 и для частиц с R=5 нм n/n 0≈0, 95, для R=10 нм n/n 0≈0, 37, а для R=20 нм n/n 0≈10 -4. Отсюда следует, что ввиду экспоненциально сильной зависимости n/n 0 от V вблизи R=Rc≈10 нм происходит фактически скачок от равномерного распределения частиц по высоте (при R Rc) к их оседанию на дне сосуда (при R Rc). Частицы более легкие, чем жидкость, например, капельки жира в молоке), будут не оседать, а всплывать. Частицы достаточно большого размера будут оседать (при > 0) или всплывать (при < 0) в жидкости.
 Характерное время расслоения суспензии или эмульсии зависит от R, - 0 и вязкости жидкости . В приведенном примере для наночастиц серебра с R = 20 нм Даже в воздухе с гораздо меньшей вязкостью, чем в воде, эта взвесь будет оседать около двух суток (в совершенно спокойных условиях). Средняя скорость конвективных потоков в жидкости, а тем более в воздухе в обычных условиях гораздо выше 10 -6 м/с. Для ускорения седиментационных процессов применяют центрифугирование, которое создает ускорение до 106 раз превышающее g, что резко сокращает продолжительность процесса.
Характерное время расслоения суспензии или эмульсии зависит от R, - 0 и вязкости жидкости . В приведенном примере для наночастиц серебра с R = 20 нм Даже в воздухе с гораздо меньшей вязкостью, чем в воде, эта взвесь будет оседать около двух суток (в совершенно спокойных условиях). Средняя скорость конвективных потоков в жидкости, а тем более в воздухе в обычных условиях гораздо выше 10 -6 м/с. Для ускорения седиментационных процессов применяют центрифугирование, которое создает ускорение до 106 раз превышающее g, что резко сокращает продолжительность процесса.
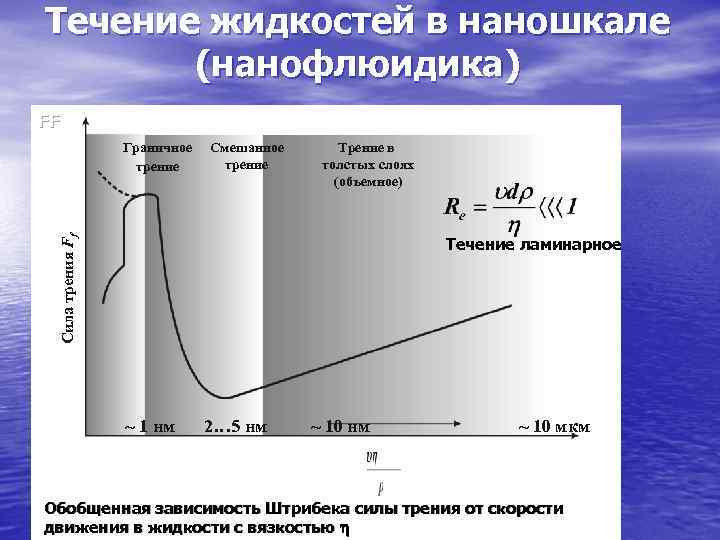
 Течение жидкостей в наношкале (нанофлюидика) FF Граничное Смешанное Трение в трение толстых слоях (объемное) Сила трения Ff Течение ламинарное ~ 1 нм 2… 5 нм ~ 10 нм ~ 10 мкм Обобщенная зависимость Штрибека силы трения от скорости движения в жидкости с вязкостью
Течение жидкостей в наношкале (нанофлюидика) FF Граничное Смешанное Трение в трение толстых слоях (объемное) Сила трения Ff Течение ламинарное ~ 1 нм 2… 5 нм ~ 10 нм ~ 10 мкм Обобщенная зависимость Штрибека силы трения от скорости движения в жидкости с вязкостью
 Движение жидкостей (особенно содержащих высокомолекулярные соединения, наночастицы) в наноразмерных каналах, порах, мембранах, нанопористых средах сильно отличается от макроскопического. Для краткости всю специфику подобных ситуаций обозначают термином «наножидкости» или «нанофлюидика» . Ясно, что когда размер канала становится соизмеримым с размером движущихся по нему молекул или наночастиц, свойства жидкости сильно изменятся по сравнению с объемными. Это отражает обобщенная зависимость Штрибека.
Движение жидкостей (особенно содержащих высокомолекулярные соединения, наночастицы) в наноразмерных каналах, порах, мембранах, нанопористых средах сильно отличается от макроскопического. Для краткости всю специфику подобных ситуаций обозначают термином «наножидкости» или «нанофлюидика» . Ясно, что когда размер канала становится соизмеримым с размером движущихся по нему молекул или наночастиц, свойства жидкости сильно изменятся по сравнению с объемными. Это отражает обобщенная зависимость Штрибека.
 Важнейшими особенностями движения жидкостей в наношкале можно считать: 1. Ламинарный (безвихревой) характер течения при любых реальных условиях, поскольку в наносистемах оно всегда характеризуется очень малыми значениями безразмерного числа Рейнольдса (физически оно означает отношение сил инерции к силам вязкости в жидкости) (здесь - скорость течения, d – эффективный поперечный размер канала или движущегося тела, и - плотность и вязкость жидкости соответственно). В этих условиях уравнение Навье-Стокса упростится до , имеющего известные решения для всех простых случаев (напомним, что переход к турбулентному течению 3
Важнейшими особенностями движения жидкостей в наношкале можно считать: 1. Ламинарный (безвихревой) характер течения при любых реальных условиях, поскольку в наносистемах оно всегда характеризуется очень малыми значениями безразмерного числа Рейнольдса (физически оно означает отношение сил инерции к силам вязкости в жидкости) (здесь - скорость течения, d – эффективный поперечный размер канала или движущегося тела, и - плотность и вязкость жидкости соответственно). В этих условиях уравнение Навье-Стокса упростится до , имеющего известные решения для всех простых случаев (напомним, что переход к турбулентному течению 3
 Продолжение 2. В большинстве случаев движение наножидкости по каналу приводит к образованию двойного электрического слоя в пристеночных слоях. Вследствие наличия зарядов в жидкости наложение внешнего электрического поля Е вызывает электроосмос – её движение вдоль канала со скоростью = Е/ (здесь - диэлектрическая проницаемость жидкости, - приповерхностный потенциал), т. е. реализуется нанонасос. 3. Движение жидкости в канале, обтекание препятствия и т. п. сопровождается образованием заторможенного приповерхностного (граничного слоя жидкости). Обычно он имеет толщину в несколько молекул, что составляет единицы (для высокомолекулярных жидкостей – до десятка) нанометров. Все процессы массо- и теплопереноса в этом слое происходят намного медленнее, чем в подвижных слоях. Если характерный размер гидродинамической задачи (например, диаметр капилляра или движущейся в потоке наночастицы)) приблизится к , все характеристики жидкости и процессов в ней резко изменятся, что и отражает эмпирическая кривая Штрибека для гидравлического сопротивления в области малых размеров.
Продолжение 2. В большинстве случаев движение наножидкости по каналу приводит к образованию двойного электрического слоя в пристеночных слоях. Вследствие наличия зарядов в жидкости наложение внешнего электрического поля Е вызывает электроосмос – её движение вдоль канала со скоростью = Е/ (здесь - диэлектрическая проницаемость жидкости, - приповерхностный потенциал), т. е. реализуется нанонасос. 3. Движение жидкости в канале, обтекание препятствия и т. п. сопровождается образованием заторможенного приповерхностного (граничного слоя жидкости). Обычно он имеет толщину в несколько молекул, что составляет единицы (для высокомолекулярных жидкостей – до десятка) нанометров. Все процессы массо- и теплопереноса в этом слое происходят намного медленнее, чем в подвижных слоях. Если характерный размер гидродинамической задачи (например, диаметр капилляра или движущейся в потоке наночастицы)) приблизится к , все характеристики жидкости и процессов в ней резко изменятся, что и отражает эмпирическая кривая Штрибека для гидравлического сопротивления в области малых размеров.
 Капиллярные явления в наношкале
Капиллярные явления в наношкале
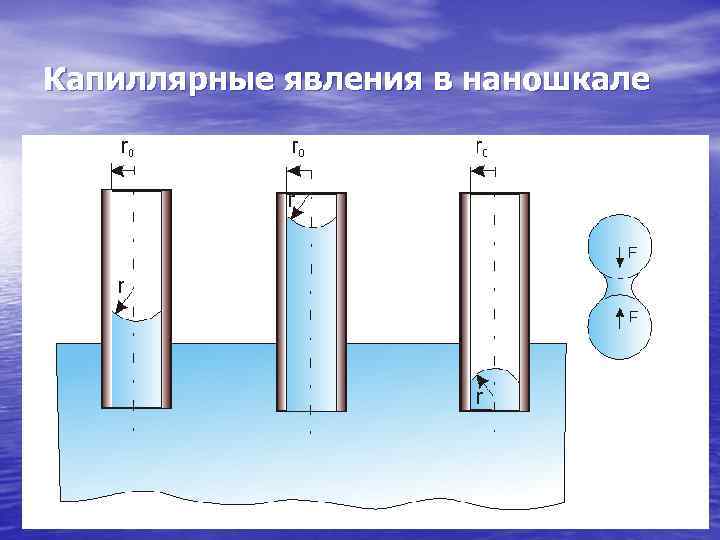
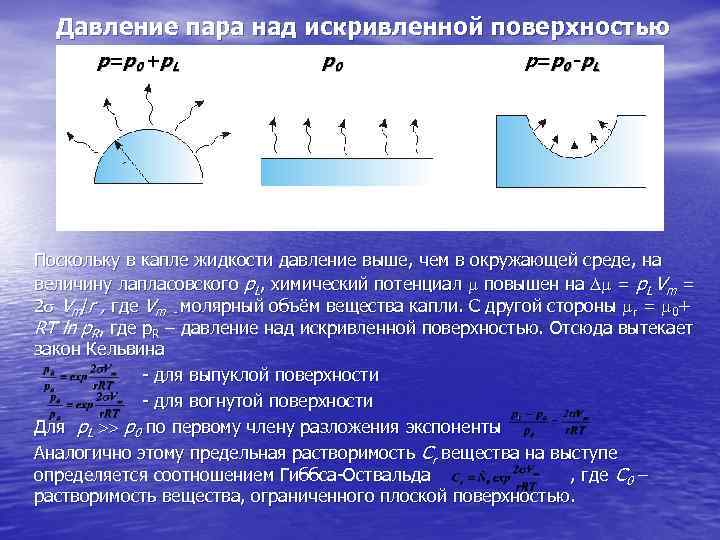
 Капиллярные явления есть частный случай поверхностных явлений с участием искривленных поверхностей контактирующих тел, одно из которых жидкое. Из самого названия следует, что оно ярко проявляется в узких каналах, порах, капиллярах. Искривленная поверхность жидкости или твердого тела создает дополнительное (лапласовское) давление р. L, зависящее от величины и знака кривизны поверхности р. L = ± (1/r 1+1/r 2), где - поверхностное натяжение, r 1 и r 2 - главные радиусы кривизны в двух взаимно перпендикулярных направлениях. Если r 1=r 2=r, то р. L = ± 2 /r. Выпуклая поверхность создает положительное давление, а вогнутая – отрицательное (оба направлены к центру кривизны). При больших значениях и малых r лапласовское давление может достигать значительных величин. Так, например, для капельки воды ( = 0, 075 Дж/м 2) диаметром 2 r = 3 нм р. L = 108 Па, т. е. в 1000 раз больше атмосферного, а для такой же капельки ртути ( = 0, 45 Дж/м 2) еще в 6 раз выше. Закон Лапласа сформулирован в макроскопических терминах, поэтому справедлив для r а, где а – характерный размер действия молекулярных сил (~ несколько нанометров). Капиллярные силы заставляют подниматься жидкость в тонких капиллярах (при смачивании стенок) и притягиваться смоченные наночастицы друг к другу.
Капиллярные явления есть частный случай поверхностных явлений с участием искривленных поверхностей контактирующих тел, одно из которых жидкое. Из самого названия следует, что оно ярко проявляется в узких каналах, порах, капиллярах. Искривленная поверхность жидкости или твердого тела создает дополнительное (лапласовское) давление р. L, зависящее от величины и знака кривизны поверхности р. L = ± (1/r 1+1/r 2), где - поверхностное натяжение, r 1 и r 2 - главные радиусы кривизны в двух взаимно перпендикулярных направлениях. Если r 1=r 2=r, то р. L = ± 2 /r. Выпуклая поверхность создает положительное давление, а вогнутая – отрицательное (оба направлены к центру кривизны). При больших значениях и малых r лапласовское давление может достигать значительных величин. Так, например, для капельки воды ( = 0, 075 Дж/м 2) диаметром 2 r = 3 нм р. L = 108 Па, т. е. в 1000 раз больше атмосферного, а для такой же капельки ртути ( = 0, 45 Дж/м 2) еще в 6 раз выше. Закон Лапласа сформулирован в макроскопических терминах, поэтому справедлив для r а, где а – характерный размер действия молекулярных сил (~ несколько нанометров). Капиллярные силы заставляют подниматься жидкость в тонких капиллярах (при смачивании стенок) и притягиваться смоченные наночастицы друг к другу.
 Давление пара над искривленной поверхностью р=р0 +р. L р0 р = р 0 -р L Поскольку в капле жидкости давление выше, чем в окружающей среде, на величину лапласовского p. L, химический потенциал повышен на = p. L Vm = 2 Vm/r , где Vm - молярный объём вещества капли. С другой стороны r = 0+ RT ln p. R, где р. R – давление над искривленной поверхностью. Отсюда вытекает закон Кельвина - для выпуклой поверхности - для вогнутой поверхности Для р. L р0 по первому члену разложения экспоненты Аналогично этому предельная растворимость Сr вещества на выступе определяется соотношением Гиббса-Оствальда , где С 0 – растворимость вещества, ограниченного плоской поверхностью.
Давление пара над искривленной поверхностью р=р0 +р. L р0 р = р 0 -р L Поскольку в капле жидкости давление выше, чем в окружающей среде, на величину лапласовского p. L, химический потенциал повышен на = p. L Vm = 2 Vm/r , где Vm - молярный объём вещества капли. С другой стороны r = 0+ RT ln p. R, где р. R – давление над искривленной поверхностью. Отсюда вытекает закон Кельвина - для выпуклой поверхности - для вогнутой поверхности Для р. L р0 по первому члену разложения экспоненты Аналогично этому предельная растворимость Сr вещества на выступе определяется соотношением Гиббса-Оствальда , где С 0 – растворимость вещества, ограниченного плоской поверхностью.
 Явления переноса в наноструктурах • Электрический ток – перенос заряда • Диффузия – перенос массы • Теплопроводность – перенос теплоты • Вязкость – перенос импульса Обобщенная формула для всех: I=-K grad U
Явления переноса в наноструктурах • Электрический ток – перенос заряда • Диффузия – перенос массы • Теплопроводность – перенос теплоты • Вязкость – перенос импульса Обобщенная формула для всех: I=-K grad U
 Большая группа явлений (наиболее известные и значимые представители которых поименованы выше) называется в физике явлениями переноса и может быть рассмотрена с общих позиций. Все они реализуются под действием градиента какого- либо термодинамического потенциала в ходе неравновесного процесса, осуществляющего перенос в направлении, противоположном этому градиенту. При малых отклонениях системы от термодинамического равновесия поток некоторой величины I (количественной меры переноса заряда, массы, энергии, импульса, энтропии и т. д. через единицу площади в единицу времени) связан с обобщенной силой – градиентом обобщенного потенциала U (электрического , концентрации С, температуры Т, скорости потока и т. д. ) простым феноменологическим уравнением Ii = - Ki grad U, где Ki – коэффициент переноса. Термодинамика неравновесных процессов дает общую феноменологическую теорию таких процессов, а физическая кинетика позволяет вычислять кинетические коэффициенты в рамках той или иной микроскопической модели путем решения соответствующих кинетических уравнений.
Большая группа явлений (наиболее известные и значимые представители которых поименованы выше) называется в физике явлениями переноса и может быть рассмотрена с общих позиций. Все они реализуются под действием градиента какого- либо термодинамического потенциала в ходе неравновесного процесса, осуществляющего перенос в направлении, противоположном этому градиенту. При малых отклонениях системы от термодинамического равновесия поток некоторой величины I (количественной меры переноса заряда, массы, энергии, импульса, энтропии и т. д. через единицу площади в единицу времени) связан с обобщенной силой – градиентом обобщенного потенциала U (электрического , концентрации С, температуры Т, скорости потока и т. д. ) простым феноменологическим уравнением Ii = - Ki grad U, где Ki – коэффициент переноса. Термодинамика неравновесных процессов дает общую феноменологическую теорию таких процессов, а физическая кинетика позволяет вычислять кинетические коэффициенты в рамках той или иной микроскопической модели путем решения соответствующих кинетических уравнений.
 Легко видеть, что простейшие физические законы, описывающие явления переноса (закон Ома, 1 -ый закон Фика, 1 -ый закон Фурье, формула Пуазейля, см. ниже), являются частными случаями обобщенного уравнения переноса. Закон Ома [Кл/м 2 с], 1 -ый закон Фика [кг/м 2 с], 1 -ый закон Фурье [Дж/м 2 с] , формула Пуазейля [ м 3 /м 2 с ]. Рассмотрим теперь на примере закона Ома микроскопические подходы к интерпретации и количественному определению соответствующего коэффициента переноса – удельной электропроводности . Легко показать, что в рамках классического рассмотрения = е n , где е – заряд носителя (электрона, иона, куперовской пары и др. ), n - концентрация носителей, - их подвижность (средняя скорость в единичном поле). Заметим, что - пропорциональна длине свободного пробега носителя между соударениями с рассеивающими центрами. Аналогичные соотношения между характеристиками ансамбля микроскопических объектов –носителей и макрокинетическим коэффициентом переноса можно ввести и для других кинетических явлений (более подробно см. учебники физики).
Легко видеть, что простейшие физические законы, описывающие явления переноса (закон Ома, 1 -ый закон Фика, 1 -ый закон Фурье, формула Пуазейля, см. ниже), являются частными случаями обобщенного уравнения переноса. Закон Ома [Кл/м 2 с], 1 -ый закон Фика [кг/м 2 с], 1 -ый закон Фурье [Дж/м 2 с] , формула Пуазейля [ м 3 /м 2 с ]. Рассмотрим теперь на примере закона Ома микроскопические подходы к интерпретации и количественному определению соответствующего коэффициента переноса – удельной электропроводности . Легко показать, что в рамках классического рассмотрения = е n , где е – заряд носителя (электрона, иона, куперовской пары и др. ), n - концентрация носителей, - их подвижность (средняя скорость в единичном поле). Заметим, что - пропорциональна длине свободного пробега носителя между соударениями с рассеивающими центрами. Аналогичные соотношения между характеристиками ансамбля микроскопических объектов –носителей и макрокинетическим коэффициентом переноса можно ввести и для других кинетических явлений (более подробно см. учебники физики).
 Особенности диффузии в наноструктурах Наряду с диффузией, вызванной разностью концентраций в соседних микробъёмах, существует и диффузия под действием других движущих сил (электрического поля, упругих деформаций, разности температур, химических потенциалов и др. ). Она также происходит в результате почти случайного блуждания частиц, но имеет предпочтительное направление, задаваемое градиентом внешнего поля. В этом случае процесс правильнее называть миграцией. Диффузионный поток будет тогда определяться обобщенным законом Фика Учитывая, что при малых размерах объекта grad U может быть очень большим (в одномерном случае ) миграционные потоки могут стать очень значительными по отношению к чисто диффузионным. Другой важный момент определяется квадратичной зависимостью характерного времени диффузии от расстояния R, на которое распространяется диффузионный фронт: =АR 2/D, где А – безразмерный коэффициент ~ 1. Ясно, что при уменьшении R от макромасштабов до нано – величина упадет на много порядков величин.
Особенности диффузии в наноструктурах Наряду с диффузией, вызванной разностью концентраций в соседних микробъёмах, существует и диффузия под действием других движущих сил (электрического поля, упругих деформаций, разности температур, химических потенциалов и др. ). Она также происходит в результате почти случайного блуждания частиц, но имеет предпочтительное направление, задаваемое градиентом внешнего поля. В этом случае процесс правильнее называть миграцией. Диффузионный поток будет тогда определяться обобщенным законом Фика Учитывая, что при малых размерах объекта grad U может быть очень большим (в одномерном случае ) миграционные потоки могут стать очень значительными по отношению к чисто диффузионным. Другой важный момент определяется квадратичной зависимостью характерного времени диффузии от расстояния R, на которое распространяется диффузионный фронт: =АR 2/D, где А – безразмерный коэффициент ~ 1. Ясно, что при уменьшении R от макромасштабов до нано – величина упадет на много порядков величин.
 Диффузия по свободным поверхностям и границам зерен Сравнение поверхностной, параллельной межзеренным границам и объемной диффузии тория в вольфраме при равных D 0 Физико-химические основы материаловедения / Готтштайн Г. ; пер. с англ. К. Н. Золотовой, Д. О. Чаркина; под ред. В. П. Зломанова. – М. : БИНОМ. Лаборатория знаний, 2009. – 400 с.
Диффузия по свободным поверхностям и границам зерен Сравнение поверхностной, параллельной межзеренным границам и объемной диффузии тория в вольфраме при равных D 0 Физико-химические основы материаловедения / Готтштайн Г. ; пер. с англ. К. Н. Золотовой, Д. О. Чаркина; под ред. В. П. Зломанова. – М. : БИНОМ. Лаборатория знаний, 2009. – 400 с.
 Теплоперенос в наношкале • Существует 3 вида теплопереноса, способных идти параллельно: Qсуммарная = Q теплопров. + Q конвект. + Q излучен. 1. Теплопроводность (в твердых телах, гелях, заторможенных слоях жидкости и т. п. ); 2. Конвекция (в движущихся слоях газов и жидкостей) 3. Излучение (путем обмена энергией с помощью электромагнитных волн преимущественно инфракрасного диапазона). Ввиду очень сильной зависимости интенсивности излучательного теплообмена от температуры (по четвертой степени от нее), она не имеет определяющего значения для биохимических реакций в живых организмах.
Теплоперенос в наношкале • Существует 3 вида теплопереноса, способных идти параллельно: Qсуммарная = Q теплопров. + Q конвект. + Q излучен. 1. Теплопроводность (в твердых телах, гелях, заторможенных слоях жидкости и т. п. ); 2. Конвекция (в движущихся слоях газов и жидкостей) 3. Излучение (путем обмена энергией с помощью электромагнитных волн преимущественно инфракрасного диапазона). Ввиду очень сильной зависимости интенсивности излучательного теплообмена от температуры (по четвертой степени от нее), она не имеет определяющего значения для биохимических реакций в живых организмах.
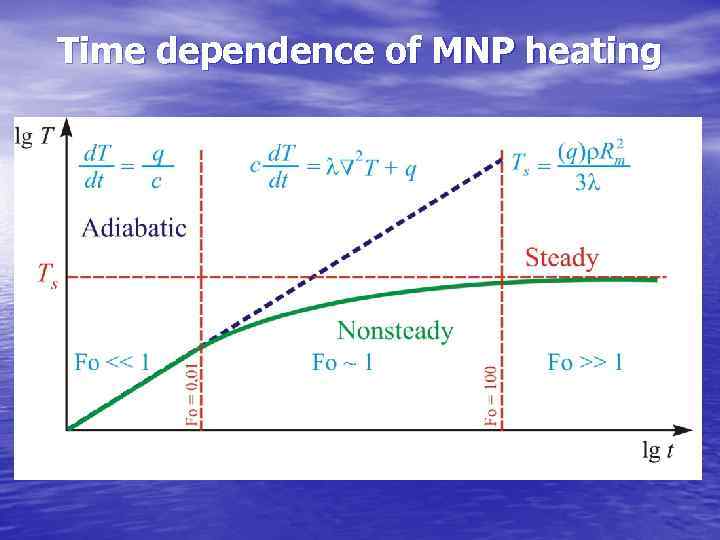
 Некоторые особенности теплопереноса в наношкале • Интенсивность стационарного теплопереноса при теплопроводности и конвекции определяется разностью температур и коэффициентами теплопроводности или теплоотдачи соответственно. Первый может отличаться в наношкале от макроскопического из-за изменений фононного спектра в наноструктурах, а второй – из-за сопоставимости толщины заторможенного граничного слоя теплоностителя с характерными размерами наноструктуры. • Режим нестационарной (неустановившейся) теплопроводности определяется величиной критерия Фурье (безразмерного времени) Fo = t/tc , где tc = R 2/K-характерное время термической диффузии, K – коэффициент температуропроводности. • При Fo значительно меньше 1 реализуется адиабатический режим, при Fo гораздо больше 1 – режим с интенсивным теплообменом и сильным снижением градиента температуры (по сравнению с адиабатическим). • Из-за малости R в наноструктурах безразмерное время течет для них быстро. Так, для частиц с R=10 нм, взвешенных в воде или водном растворе, Fo=1 соответствует реальному промежутку времени порядка 1 нс.
Некоторые особенности теплопереноса в наношкале • Интенсивность стационарного теплопереноса при теплопроводности и конвекции определяется разностью температур и коэффициентами теплопроводности или теплоотдачи соответственно. Первый может отличаться в наношкале от макроскопического из-за изменений фононного спектра в наноструктурах, а второй – из-за сопоставимости толщины заторможенного граничного слоя теплоностителя с характерными размерами наноструктуры. • Режим нестационарной (неустановившейся) теплопроводности определяется величиной критерия Фурье (безразмерного времени) Fo = t/tc , где tc = R 2/K-характерное время термической диффузии, K – коэффициент температуропроводности. • При Fo значительно меньше 1 реализуется адиабатический режим, при Fo гораздо больше 1 – режим с интенсивным теплообменом и сильным снижением градиента температуры (по сравнению с адиабатическим). • Из-за малости R в наноструктурах безразмерное время течет для них быстро. Так, для частиц с R=10 нм, взвешенных в воде или водном растворе, Fo=1 соответствует реальному промежутку времени порядка 1 нс.
 Time dependence of MNP heating
Time dependence of MNP heating
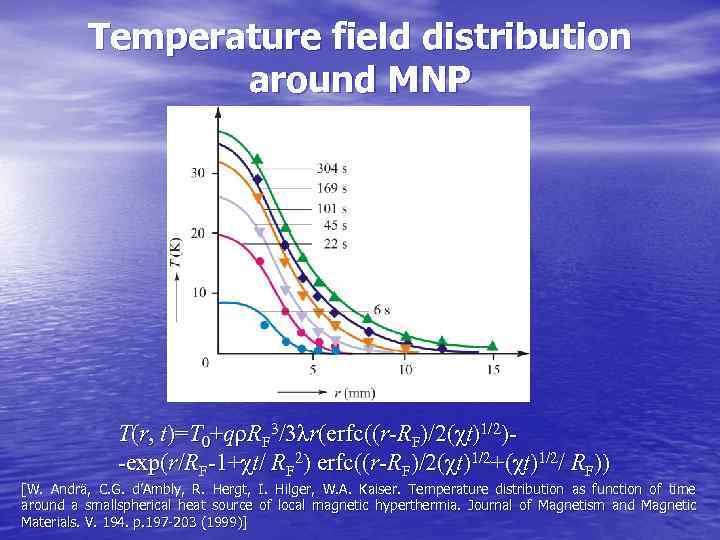
 Temperature field distribution around MNP T(r, t)=T 0+qρRF 3/3λr(erfc((r-RF)/2(χt)1/2)- -exp(r/RF-1+χt/ RF 2) erfc((r-RF)/2(χt)1/2+(χt)1/2/ RF)) [W. Andrä, C. G. d’Ambly, R. Hergt, I. Hilger, W. A. Kaiser. Temperature distribution as function of time around a smallspherical heat source of local magnetic hyperthermia. Journal of Magnetism and Magnetic Materials. V. 194. p. 197 -203 (1999)]
Temperature field distribution around MNP T(r, t)=T 0+qρRF 3/3λr(erfc((r-RF)/2(χt)1/2)- -exp(r/RF-1+χt/ RF 2) erfc((r-RF)/2(χt)1/2+(χt)1/2/ RF)) [W. Andrä, C. G. d’Ambly, R. Hergt, I. Hilger, W. A. Kaiser. Temperature distribution as function of time around a smallspherical heat source of local magnetic hyperthermia. Journal of Magnetism and Magnetic Materials. V. 194. p. 197 -203 (1999)]
 Размерные эффекты в магнетизме
Размерные эффекты в магнетизме
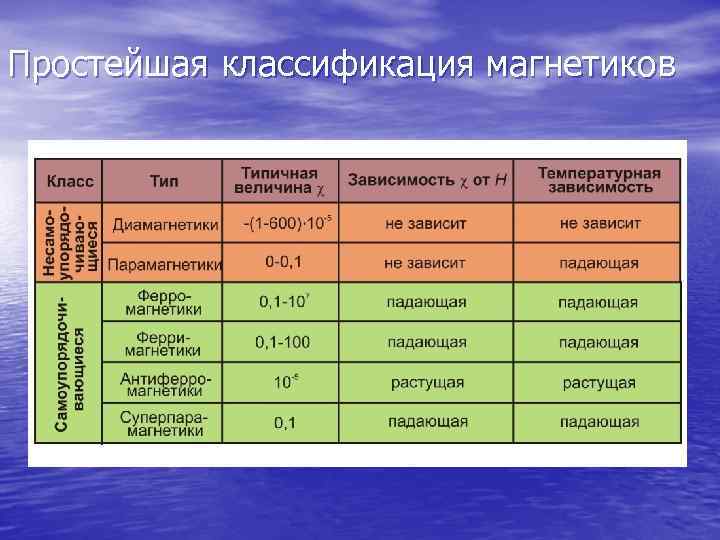
 Простейшая классификация магнетиков
Простейшая классификация магнетиков
 Задолго до установления микроскопической природы магнитных свойств веществ их классифицировали по микроскопическим характеристикам – величине магнитной проницаемости, поведению в магнитном поле, температурным зависимостям и др. Основные типы веществ согласно такой феноменологической классификации приведены в таблице. До последней трети прошлого века размерные эффекты в магнитных свойствах веществ систематически не исследовались. Результаты, полученные в последние десятилетия свидетельствуют, что уменьшение характерных размеров структуры может сильно (иногда драматически) повлиять на магнитные свойства как неупорядочивающихся, так и самоупорядочивающихся (по магнитным моментам) материалов. Некоторые примеры такого поведения будут даны ниже.
Задолго до установления микроскопической природы магнитных свойств веществ их классифицировали по микроскопическим характеристикам – величине магнитной проницаемости, поведению в магнитном поле, температурным зависимостям и др. Основные типы веществ согласно такой феноменологической классификации приведены в таблице. До последней трети прошлого века размерные эффекты в магнитных свойствах веществ систематически не исследовались. Результаты, полученные в последние десятилетия свидетельствуют, что уменьшение характерных размеров структуры может сильно (иногда драматически) повлиять на магнитные свойства как неупорядочивающихся, так и самоупорядочивающихся (по магнитным моментам) материалов. Некоторые примеры такого поведения будут даны ниже.
 Некоторые определения Магнитный момент Намагниченность
Некоторые определения Магнитный момент Намагниченность
 Магнетики Все вещества в той или иной степени магнитны и взаимодействуют с внешним магнитным полем (МП). Одна из основных характеристик магнетика – магнитный момент единицы объема: Магнитный момент Намагниченность Объем – магнитная восприимчивость (тензор 2 -го ранга) Суммарное магнитное поле в присутствии вещества: – относительная магнитная проницаемость вещества
Магнетики Все вещества в той или иной степени магнитны и взаимодействуют с внешним магнитным полем (МП). Одна из основных характеристик магнетика – магнитный момент единицы объема: Магнитный момент Намагниченность Объем – магнитная восприимчивость (тензор 2 -го ранга) Суммарное магнитное поле в присутствии вещества: – относительная магнитная проницаемость вещества
![> Магнитное поле в присутствии вещества Напряженность МП H [A/m] > Магнитное поле в присутствии вещества Напряженность МП H [A/m]](https://present5.com/presentation/3/176394115_349362760.pdf-img/176394115_349362760.pdf-49.jpg) Магнитное поле в присутствии вещества Напряженность МП H [A/m] всегда пропорциональна намагничивающему току I Индукция МП В есть сумма допустим, что - Магнитная восприимчивость материала - Магнитная проницаемость; Система СГС , , а , при 1 Тл = 104 гс; при µ = 1 1 Тл = 104 Э
Магнитное поле в присутствии вещества Напряженность МП H [A/m] всегда пропорциональна намагничивающему току I Индукция МП В есть сумма допустим, что - Магнитная восприимчивость материала - Магнитная проницаемость; Система СГС , , а , при 1 Тл = 104 гс; при µ = 1 1 Тл = 104 Э
 Поведение вещества в магнитном поле можно рассматривать с макроскопических позиций, используя известные феноменологические закономерности и опираясь на уравнения Максвелла и законы термодинамики. Более глубокие представления о природе магнитных свойств можно получить на основе квантовой механики и статистики. В макроскопическом подходе важную роль играет намагниченность – векторная сумма магнитных моментов элементов структуры , нормированная на объём V (скаляр): Вектор можно связать с приложенным магнитным полем через магнитную восприимчивость материала (тензор второго ранга): В отсутствие магнитного поля отдельные магнитные моменты электронов, атомов, молекул, наночастиц и т. д. Могут быть хаотизированы по направлениям (вследствие тепловых флуктуаций, стремления к росту энтропии и понижению свободной энергии Гиббса), а в некоторых (довольно редких) случаях – самоупорядочены в пределах некоторой области, называемой магнитным доменом. Самоупорядочивающиеся по магнитным моментам вещества называются ферромагнетиками (независимо от того, содержат ли они в своем составе атомы железа или нет). В присутствии вещества индукция магнитного поля складывается (векторно!) из двух составляющих: намагничивающего поля в вакууме и поля магнитных моментов атомов : где – относительная магнитная проницаемость вещества (тензор второго ранга).
Поведение вещества в магнитном поле можно рассматривать с макроскопических позиций, используя известные феноменологические закономерности и опираясь на уравнения Максвелла и законы термодинамики. Более глубокие представления о природе магнитных свойств можно получить на основе квантовой механики и статистики. В макроскопическом подходе важную роль играет намагниченность – векторная сумма магнитных моментов элементов структуры , нормированная на объём V (скаляр): Вектор можно связать с приложенным магнитным полем через магнитную восприимчивость материала (тензор второго ранга): В отсутствие магнитного поля отдельные магнитные моменты электронов, атомов, молекул, наночастиц и т. д. Могут быть хаотизированы по направлениям (вследствие тепловых флуктуаций, стремления к росту энтропии и понижению свободной энергии Гиббса), а в некоторых (довольно редких) случаях – самоупорядочены в пределах некоторой области, называемой магнитным доменом. Самоупорядочивающиеся по магнитным моментам вещества называются ферромагнетиками (независимо от того, содержат ли они в своем составе атомы железа или нет). В присутствии вещества индукция магнитного поля складывается (векторно!) из двух составляющих: намагничивающего поля в вакууме и поля магнитных моментов атомов : где – относительная магнитная проницаемость вещества (тензор второго ранга).
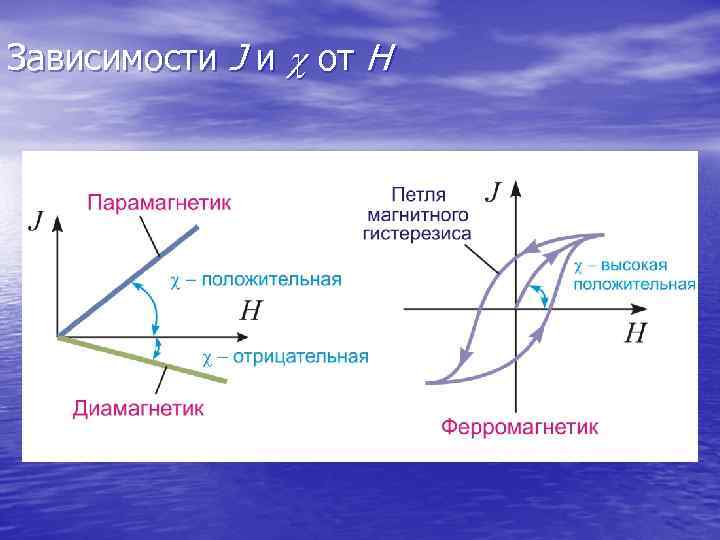
 Зависимости J и c от H
Зависимости J и c от H
 Behavior of Dia-, Para-, Ferro- and Superparamagnetics in MF Dia- Para- Ferro- Superpara- [Q. A. Pankhurst, J. Connolly, S. K. Jones, J. Dobson. Applications of magnetic nanoparticles in biomedicine. J. Phys. D: Appl. Phys. V. 36. p. R 167–R 181 (2003)]
Behavior of Dia-, Para-, Ferro- and Superparamagnetics in MF Dia- Para- Ferro- Superpara- [Q. A. Pankhurst, J. Connolly, S. K. Jones, J. Dobson. Applications of magnetic nanoparticles in biomedicine. J. Phys. D: Appl. Phys. V. 36. p. R 167–R 181 (2003)]
 Одним из отличительных признаков различной магнитной структуры вещества являются зависимости их J и от Н. У магниторазупорядоченных материалов J меняется с Н линейно (вплоть до очень сильных полей, не достижимых в лабораторных условиях). Этому соответствуют постоянные значения и . Вещества, у которых положительны и 1 называются парамагнетиками (от латинского «возле» , «около» ), а отрицательны и 1 – диамагнетиками. Типичная величина у парамагнетиков ~10 -3, а диамагнетиков ~10 - 5. Самоупорядочивающиеся вещества называют ферромагнитными (в технике только такие материалы называют «магнитными» , а пара- и диамагнетики считаются немагнитными). К них и сильно зависят от приложенного магнитного поля и магнитной предыстории и могут достигать многих тысяч. Фактически за счет этого достигается «бесплатное» увеличение внешнего магнитного поля во много раз. В неоднородных магнитных полях пара- и ферромегнетики втягиваются в область более сильного поля, а диамагнетики – выталкиваются. Эти различия дают возможность классифицировать вещества на разные типы по их поведению во внешних магнитных полях. Температурные и размерные зависимости у них также ведут себя по-разному.
Одним из отличительных признаков различной магнитной структуры вещества являются зависимости их J и от Н. У магниторазупорядоченных материалов J меняется с Н линейно (вплоть до очень сильных полей, не достижимых в лабораторных условиях). Этому соответствуют постоянные значения и . Вещества, у которых положительны и 1 называются парамагнетиками (от латинского «возле» , «около» ), а отрицательны и 1 – диамагнетиками. Типичная величина у парамагнетиков ~10 -3, а диамагнетиков ~10 - 5. Самоупорядочивающиеся вещества называют ферромагнитными (в технике только такие материалы называют «магнитными» , а пара- и диамагнетики считаются немагнитными). К них и сильно зависят от приложенного магнитного поля и магнитной предыстории и могут достигать многих тысяч. Фактически за счет этого достигается «бесплатное» увеличение внешнего магнитного поля во много раз. В неоднородных магнитных полях пара- и ферромегнетики втягиваются в область более сильного поля, а диамагнетики – выталкиваются. Эти различия дают возможность классифицировать вещества на разные типы по их поведению во внешних магнитных полях. Температурные и размерные зависимости у них также ведут себя по-разному.
 Природа атомного магнетизма – магнетон Бора – квант магнитного момента
Природа атомного магнетизма – магнетон Бора – квант магнитного момента
 Природа магнетизма на атомарном уровне определяется наличием у элементарных частиц собственных магнитных моментов той или иной величины, а у электронов в атоме – еще и орбитальным магнитным моментом (в частном случае s-электронов он может быть равен нулю). Таким образом, магнитный момент атома является векторной суммой ядерных магнитных моментов всех нуклонов и электронных магнитных моментов. Учитывая, что ядерные магнитные моменты более чем в 1000 раз уступают по величине электронным, в первом приближении ими можно пренебречь. Естественной мерой атомных магнитных моментов является собственный магнитный момент электрона, равный магнетону Бора: Магнитный момент любого многоэлектронного атома, даже находящегося в конце Периодической таблицы Менделеева, никогда не превышает нескольких В , поскольку для уменьшения магнитной энергии атома элементарные магнитные моменты электронов стремятся установить свои вектора магнитных моментов попарно противоположно, что компенсирует их внешнее поле.
Природа магнетизма на атомарном уровне определяется наличием у элементарных частиц собственных магнитных моментов той или иной величины, а у электронов в атоме – еще и орбитальным магнитным моментом (в частном случае s-электронов он может быть равен нулю). Таким образом, магнитный момент атома является векторной суммой ядерных магнитных моментов всех нуклонов и электронных магнитных моментов. Учитывая, что ядерные магнитные моменты более чем в 1000 раз уступают по величине электронным, в первом приближении ими можно пренебречь. Естественной мерой атомных магнитных моментов является собственный магнитный момент электрона, равный магнетону Бора: Магнитный момент любого многоэлектронного атома, даже находящегося в конце Периодической таблицы Менделеева, никогда не превышает нескольких В , поскольку для уменьшения магнитной энергии атома элементарные магнитные моменты электронов стремятся установить свои вектора магнитных моментов попарно противоположно, что компенсирует их внешнее поле.
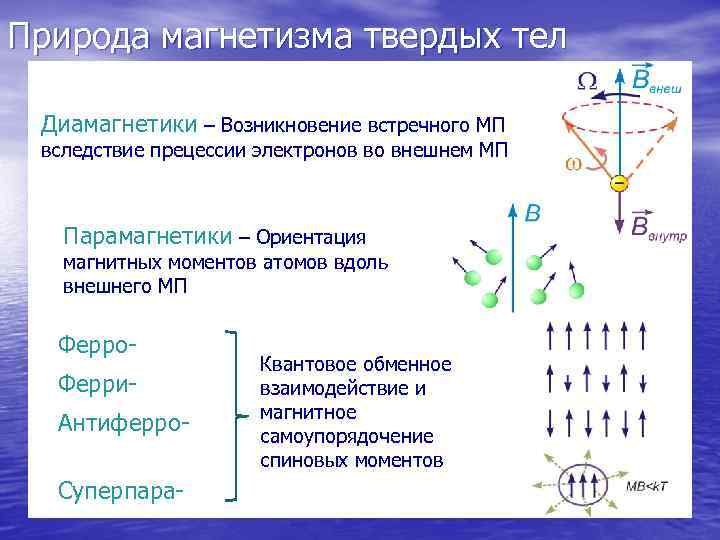
 Природа магнетизма твердых тел Диамагнетики – Возникновение встречного МП вследствие прецессии электронов во внешнем МП Парамагнетики – Ориентация магнитных моментов атомов вдоль внешнего МП Ферро- Квантовое обменное Ферри- взаимодействие и магнитное Антиферро- самоупорядочение спиновых моментов Суперпара-
Природа магнетизма твердых тел Диамагнетики – Возникновение встречного МП вследствие прецессии электронов во внешнем МП Парамагнетики – Ориентация магнитных моментов атомов вдоль внешнего МП Ферро- Квантовое обменное Ферри- взаимодействие и магнитное Антиферро- самоупорядочение спиновых моментов Суперпара-
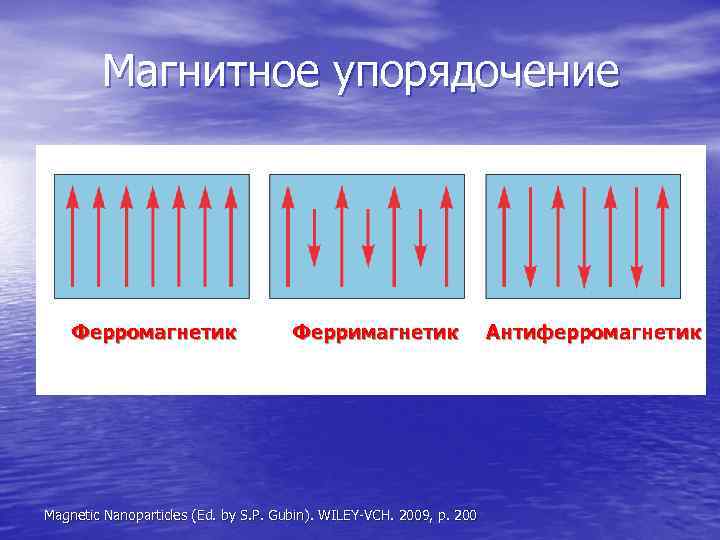
 Магнитное упорядочение Ферромагнетик Ферримагнетик Антиферромагнетик Magnetic Nanoparticles (Ed. by S. P. Gubin). WILEY-VCH. 2009, p. 200
Магнитное упорядочение Ферромагнетик Ферримагнетик Антиферромагнетик Magnetic Nanoparticles (Ed. by S. P. Gubin). WILEY-VCH. 2009, p. 200
 Одна из общих причин проявления диамагнетизма (но не единственная) – возникновение прецессии атомных магнитных моментов их вращению вокруг вектора внешнего магнитного поля. Это приводит к появлению встречного магнитного поля. Этот эффект действует всегда, но он мал и при наличии других перекрывается ими. Парамагнетизм возникает благодаря ориентации магнитных моментов атомов (если они не равны нулю в отсутствии поля) вдоль внешнего поля, что приводит к его увеличению. Все эффекты самоупорядочения обязаны сильному обменному взаимодействию электронов в соседних атомах (оно же вызывает образование прочных ковалентных связей). В ферромагнетиках выигрыш от обменного взаимодействия превышает проигрыш от понижения энтропии при упорядочении (при температурах ниже некоторой критической). Различные разновидности ферромагнетиков отличаются типом магнитного упорядочения. В ферромагнетиках две подрешетки имеют противоположную магнитную поляризацию, но не компенсируют друга, а в антиферромагнетиках компенсируют полностью. В ферромагнитных частицах достаточно малых размеров их энергия во внешнем магнитном поле может стать меньше тепловой энергии, в результате чего они, не утрачивая внутренней самоупорядоченности начинают хаотически менять направление вектора суммарной намагниченности. Ансамбль таких наночастиц будет восприниматься внешним наблюдателем как парамагнитная среда с повышенной восприимчивостью. Вследствие этого такое состояние называют суперпарамагнитным.
Одна из общих причин проявления диамагнетизма (но не единственная) – возникновение прецессии атомных магнитных моментов их вращению вокруг вектора внешнего магнитного поля. Это приводит к появлению встречного магнитного поля. Этот эффект действует всегда, но он мал и при наличии других перекрывается ими. Парамагнетизм возникает благодаря ориентации магнитных моментов атомов (если они не равны нулю в отсутствии поля) вдоль внешнего поля, что приводит к его увеличению. Все эффекты самоупорядочения обязаны сильному обменному взаимодействию электронов в соседних атомах (оно же вызывает образование прочных ковалентных связей). В ферромагнетиках выигрыш от обменного взаимодействия превышает проигрыш от понижения энтропии при упорядочении (при температурах ниже некоторой критической). Различные разновидности ферромагнетиков отличаются типом магнитного упорядочения. В ферромагнетиках две подрешетки имеют противоположную магнитную поляризацию, но не компенсируют друга, а в антиферромагнетиках компенсируют полностью. В ферромагнитных частицах достаточно малых размеров их энергия во внешнем магнитном поле может стать меньше тепловой энергии, в результате чего они, не утрачивая внутренней самоупорядоченности начинают хаотически менять направление вектора суммарной намагниченности. Ансамбль таких наночастиц будет восприниматься внешним наблюдателем как парамагнитная среда с повышенной восприимчивостью. Вследствие этого такое состояние называют суперпарамагнитным.
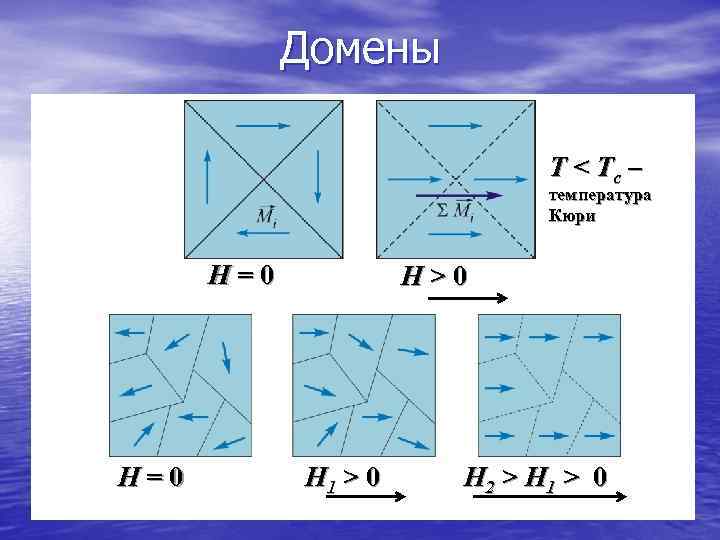
 Домены T < Tc – температура Кюри H=0 H>0 H=0 H 1 > 0 H 2 > H 1 > 0
Домены T < Tc – температура Кюри H=0 H>0 H=0 H 1 > 0 H 2 > H 1 > 0
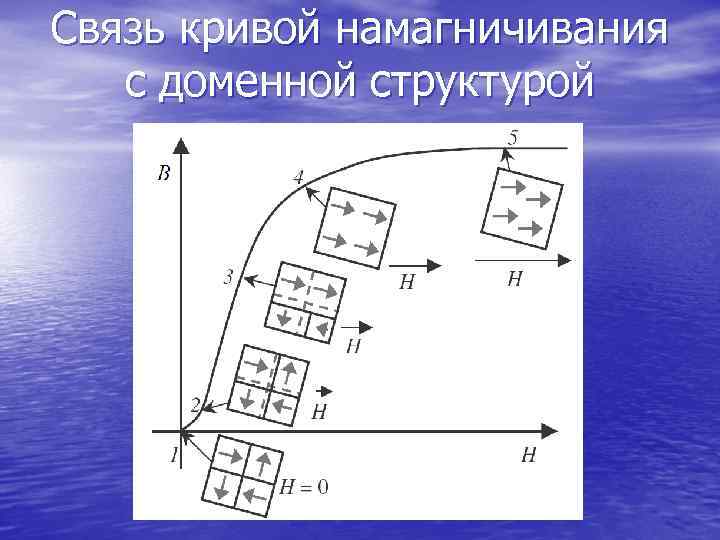
 Связь кривой намагничивания с доменной структурой
Связь кривой намагничивания с доменной структурой
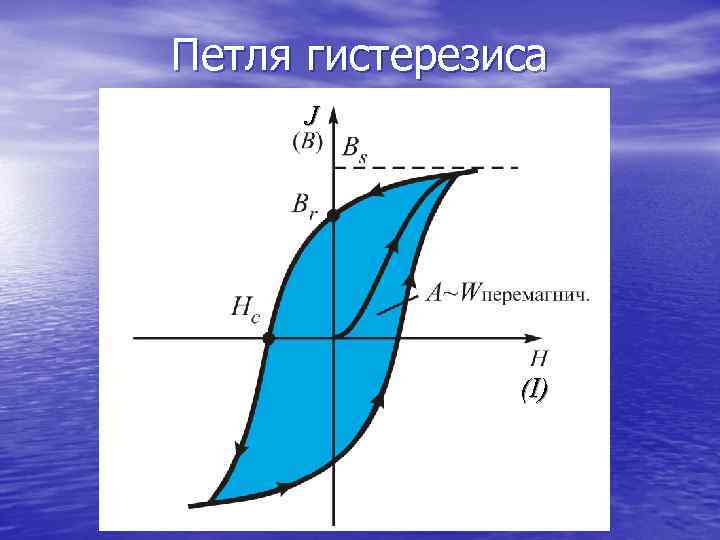
 Петля гистерезиса J (I)
Петля гистерезиса J (I)
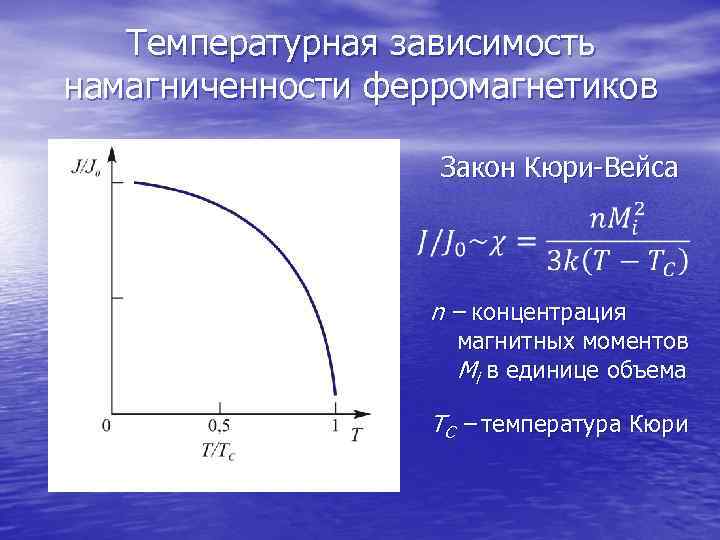
 Температурная зависимость намагниченности ферромагнетиков Закон Кюри-Вейса n – концентрация магнитных моментов Mi в единице объема TC – температура Кюри
Температурная зависимость намагниченности ферромагнетиков Закон Кюри-Вейса n – концентрация магнитных моментов Mi в единице объема TC – температура Кюри
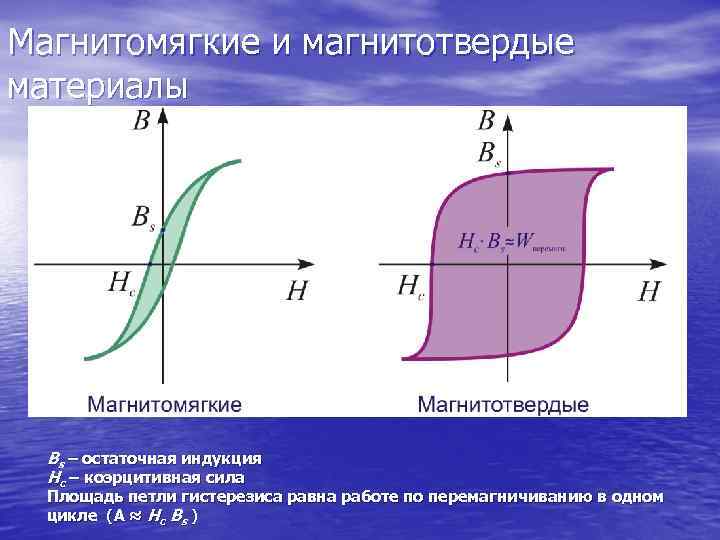
 Магнитомягкие и магнитотвердые материалы Bs – остаточная индукция Hc – коэрцитивная сила Площадь петли гистерезиса равна работе по перемагничиванию в одном цикле (А ≈ Hc Bs )
Магнитомягкие и магнитотвердые материалы Bs – остаточная индукция Hc – коэрцитивная сила Площадь петли гистерезиса равна работе по перемагничиванию в одном цикле (А ≈ Hc Bs )
 Ферромагнитные материалы принято подразделять на магнитомягкие и магнитотвердые. Первые характеризуются малой площадью петли гистерезиса S и низкими значениями характерных точек на ней: остаточной индукцией Вs и коэрцитивной силой Нс. Величина S численно равна работе А по перемагничиванию единицы объёма материала в одном цикле (А ≈ Нс Вs). Магнитомягкие материалы используют для изготовления сердечников катушек, трансформаторов, статоров и роторов электродвигателей. Чем меньше в них Нс и Вs, тем меньше потери энергии и нагрев устройства. В материалах магнитных носителей информации , постоянных магнитов и т. п. , напротив, чем больше Нс и Вs , тем выше запасаемая энергия при намагничивании. Поэтому для таких приложений стремятся сделать материалы с петлей как можно более широкой и прямоугольной.
Ферромагнитные материалы принято подразделять на магнитомягкие и магнитотвердые. Первые характеризуются малой площадью петли гистерезиса S и низкими значениями характерных точек на ней: остаточной индукцией Вs и коэрцитивной силой Нс. Величина S численно равна работе А по перемагничиванию единицы объёма материала в одном цикле (А ≈ Нс Вs). Магнитомягкие материалы используют для изготовления сердечников катушек, трансформаторов, статоров и роторов электродвигателей. Чем меньше в них Нс и Вs, тем меньше потери энергии и нагрев устройства. В материалах магнитных носителей информации , постоянных магнитов и т. п. , напротив, чем больше Нс и Вs , тем выше запасаемая энергия при намагничивании. Поэтому для таких приложений стремятся сделать материалы с петлей как можно более широкой и прямоугольной.
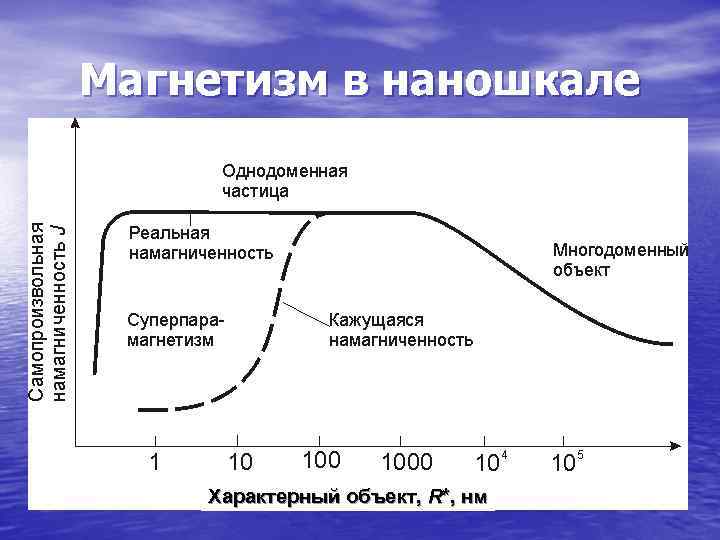
 Магнетизм в наношкале Наиболее интересны для практического применения самоупорядочивающиеся по магнитному моменту вещества (ферромагнетики: Fe, Co, Ni, Gd и их сплавы). В макрообъёмах они имеют многодоменную магнитную структуру, в которой соседние домены (самопроизвольно намагниченные области) имеют противоположную намагниченность. При уменьшении характерных размеров объекта R* до единиц микрометров обычно остается всего один домен, намагниченность которого достигает предельного насыщения (для данного материала и температуры). При очень маленьких R* ( 1 нм) величина начинает падать и магнитный порядок может исчезнуть совсем. Но еще раньше (при R* 20… 50 нм) магнитная энергия домена (или однодоменной наночастицы) становится сопоставимой или меньшей, чем её тепловая энергия (~ k. T). В результате вектор начинает хаотически переориентироваться , что для внешнего наблюдателя будет выражаться в сильном уменьшении кажущейся намагниченности среды. Такое состояние называют суперпарамагнитным. В некоторых парамагнитных материалах, напротив, уменьшение R* в области 10 нм приводит к увеличению магнитной восприимчивости. Более подробно о магнетизме в наношкале речь пойдет в модуле 9.
Магнетизм в наношкале Наиболее интересны для практического применения самоупорядочивающиеся по магнитному моменту вещества (ферромагнетики: Fe, Co, Ni, Gd и их сплавы). В макрообъёмах они имеют многодоменную магнитную структуру, в которой соседние домены (самопроизвольно намагниченные области) имеют противоположную намагниченность. При уменьшении характерных размеров объекта R* до единиц микрометров обычно остается всего один домен, намагниченность которого достигает предельного насыщения (для данного материала и температуры). При очень маленьких R* ( 1 нм) величина начинает падать и магнитный порядок может исчезнуть совсем. Но еще раньше (при R* 20… 50 нм) магнитная энергия домена (или однодоменной наночастицы) становится сопоставимой или меньшей, чем её тепловая энергия (~ k. T). В результате вектор начинает хаотически переориентироваться , что для внешнего наблюдателя будет выражаться в сильном уменьшении кажущейся намагниченности среды. Такое состояние называют суперпарамагнитным. В некоторых парамагнитных материалах, напротив, уменьшение R* в области 10 нм приводит к увеличению магнитной восприимчивости. Более подробно о магнетизме в наношкале речь пойдет в модуле 9.
 Магнетизм в наношкале Характерный объект, R*, нм
Магнетизм в наношкале Характерный объект, R*, нм
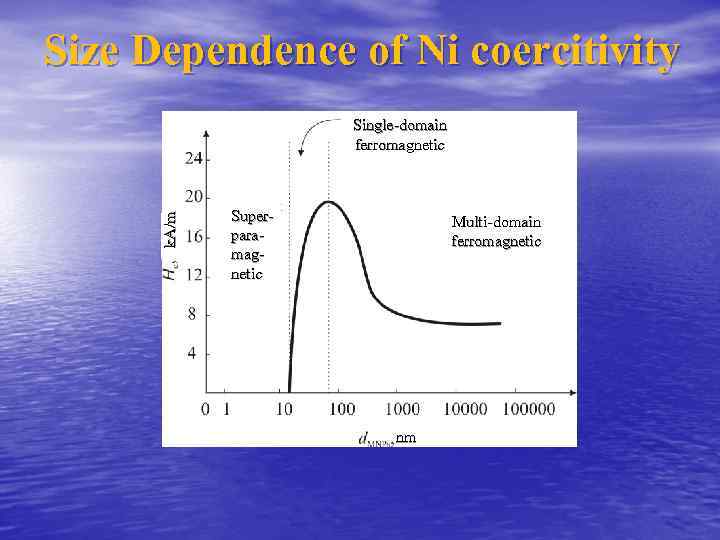
 Size Dependence of Ni coercitivity Single-domain ferromagnetic Super- k. A/m Multi-domain para- ferromagnetic mag- netic nm
Size Dependence of Ni coercitivity Single-domain ferromagnetic Super- k. A/m Multi-domain para- ferromagnetic mag- netic nm
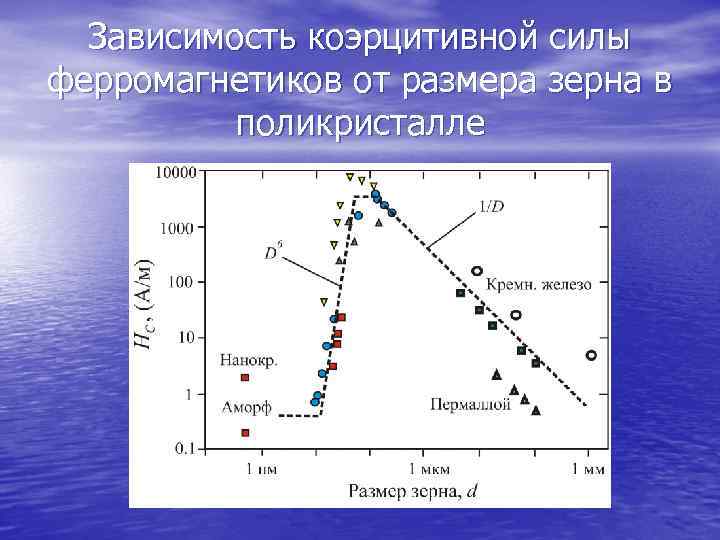
 Зависимость коэрцитивной силы ферромагнетиков от размера зерна в поликристалле
Зависимость коэрцитивной силы ферромагнетиков от размера зерна в поликристалле
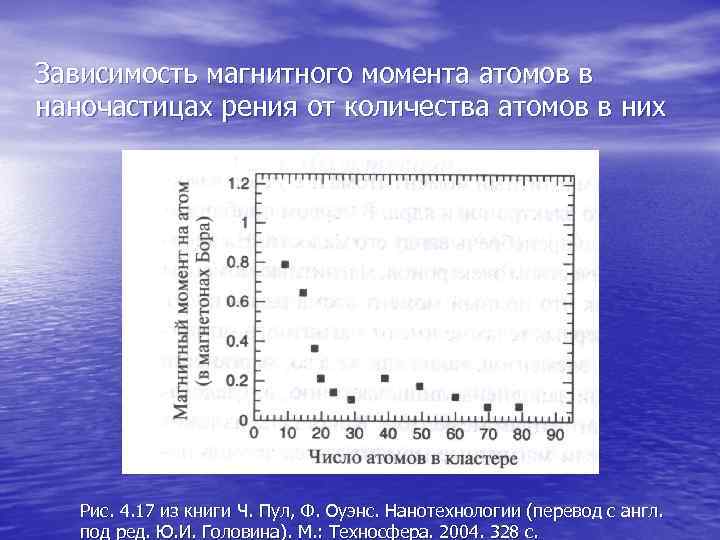
 Зависимость магнитного момента атомов в наночастицах рения от количества атомов в них Рис. 4. 17 из книги Ч. Пул, Ф. Оуэнс. Нанотехнологии (перевод с англ. под ред. Ю. И. Головина). М. : Техносфера. 2004. 328 с.
Зависимость магнитного момента атомов в наночастицах рения от количества атомов в них Рис. 4. 17 из книги Ч. Пул, Ф. Оуэнс. Нанотехнологии (перевод с англ. под ред. Ю. И. Головина). М. : Техносфера. 2004. 328 с.
 Контрольные вопросы по магнетизму • 1. Поведение вещества в магнитном поле (феноменология). Диа-, пара-, ферро- магнетики. • 2. Напряженность и индукция магнитного поля, их физ. смысл • 3. Что такое магнитный момент? Намагниченность? • 4. Какие объекты обладают магнитным моментом (макро-, микро-)?
Контрольные вопросы по магнетизму • 1. Поведение вещества в магнитном поле (феноменология). Диа-, пара-, ферро- магнетики. • 2. Напряженность и индукция магнитного поля, их физ. смысл • 3. Что такое магнитный момент? Намагниченность? • 4. Какие объекты обладают магнитным моментом (макро-, микро-)?
 Продолжение… • Взаимодействия в ансамбле магнитных частиц, свободная энергия (классическое и квантовое приближение) • Соотношение магн. моментов ядерных частиц (ядра), электронов (спиновый и орбитальный ММ) и атомов. • Природа диа- и пара- магнетизма • Самопроизвольное магнитное упорядочение, виды магнитного порядка и соответствующие классы веществ
Продолжение… • Взаимодействия в ансамбле магнитных частиц, свободная энергия (классическое и квантовое приближение) • Соотношение магн. моментов ядерных частиц (ядра), электронов (спиновый и орбитальный ММ) и атомов. • Природа диа- и пара- магнетизма • Самопроизвольное магнитное упорядочение, виды магнитного порядка и соответствующие классы веществ
 Продолжение… • Магнитный домен, однодоменное состояние наночастиц • Кривая намагничивания ферромагнетика. Что она характеризует? • 3 характеристики петли гистерезиса: намагниченность насыщения, остаточная намагниченность, коэрцитивная сила • Магнитомягкие и магнитотвердые материалы. Энергия потерь при перемагничивании
Продолжение… • Магнитный домен, однодоменное состояние наночастиц • Кривая намагничивания ферромагнетика. Что она характеризует? • 3 характеристики петли гистерезиса: намагниченность насыщения, остаточная намагниченность, коэрцитивная сила • Магнитомягкие и магнитотвердые материалы. Энергия потерь при перемагничивании
 Продолжение… • Суперпарамагнетизм. Соотношение магнитной и тепловой энергии частицы. Поведение во внешнем магнитном поле • Релаксация магнитного момента по Неелю и по Брауну • Размерные эффекты в магнетизме (частица, порошок, суспензия, объемный материал)
Продолжение… • Суперпарамагнетизм. Соотношение магнитной и тепловой энергии частицы. Поведение во внешнем магнитном поле • Релаксация магнитного момента по Неелю и по Брауну • Размерные эффекты в магнетизме (частица, порошок, суспензия, объемный материал)
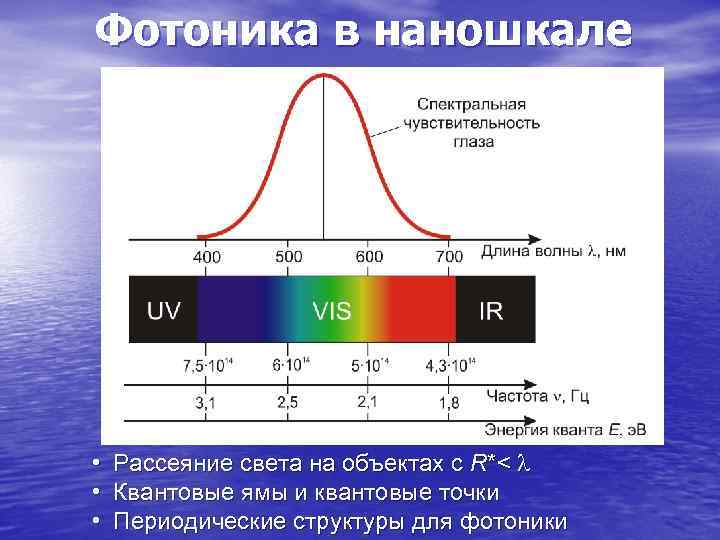
 Фотоника в наношкале • Рассеяние света на объектах с R*< • Квантовые ямы и квантовые точки • Периодические структуры для фотоники
Фотоника в наношкале • Рассеяние света на объектах с R*< • Квантовые ямы и квантовые точки • Периодические структуры для фотоники
 Важнейшей особенностью наноструктур (R* 100 нм) с точки зрения их взаимодействия со световой волной является их малость по сравнению с длиной волны как видимого света, так и ближнего ультрафиолета (не говоря уже об ИК-излучении). Это делает такие структуры в принципе неразрешимыми в самом лучшем оптическом микроскопе. Правда, это и не запрещает наблюдать отдельно расположенные центры рассеяния с R* << в прозрачных средах в темном поле (под большим углом к направлению падающего пучка), а также в переизлученном этими нанообъектами свете (в результате фотолюминесценции). Сечение рассеяния (т. е. интенсивность рассеянного света) при R* << дается формулой Релея = А(R*)6/ 4, где А – коэффициент, зависящий от диэлектрической проницаемости частицы и окружающей среды. Низкоразмерные системы, образующие квантовые проволочки, ямы (колодцы) и квантовые точки, имеют электронные дискретные спектры, зависящие от их размеров. Они широко используются для создания высокоэффективных лазеров и фотоприемников. В этих случаях эксплуатируют квантовые свойства света. Периодические структуры с шагом порядка используют в фотонике для управления световыми пучками. В этих приложениях эксплуатируют волновые свойства света.
Важнейшей особенностью наноструктур (R* 100 нм) с точки зрения их взаимодействия со световой волной является их малость по сравнению с длиной волны как видимого света, так и ближнего ультрафиолета (не говоря уже об ИК-излучении). Это делает такие структуры в принципе неразрешимыми в самом лучшем оптическом микроскопе. Правда, это и не запрещает наблюдать отдельно расположенные центры рассеяния с R* << в прозрачных средах в темном поле (под большим углом к направлению падающего пучка), а также в переизлученном этими нанообъектами свете (в результате фотолюминесценции). Сечение рассеяния (т. е. интенсивность рассеянного света) при R* << дается формулой Релея = А(R*)6/ 4, где А – коэффициент, зависящий от диэлектрической проницаемости частицы и окружающей среды. Низкоразмерные системы, образующие квантовые проволочки, ямы (колодцы) и квантовые точки, имеют электронные дискретные спектры, зависящие от их размеров. Они широко используются для создания высокоэффективных лазеров и фотоприемников. В этих случаях эксплуатируют квантовые свойства света. Периодические структуры с шагом порядка используют в фотонике для управления световыми пучками. В этих приложениях эксплуатируют волновые свойства света.
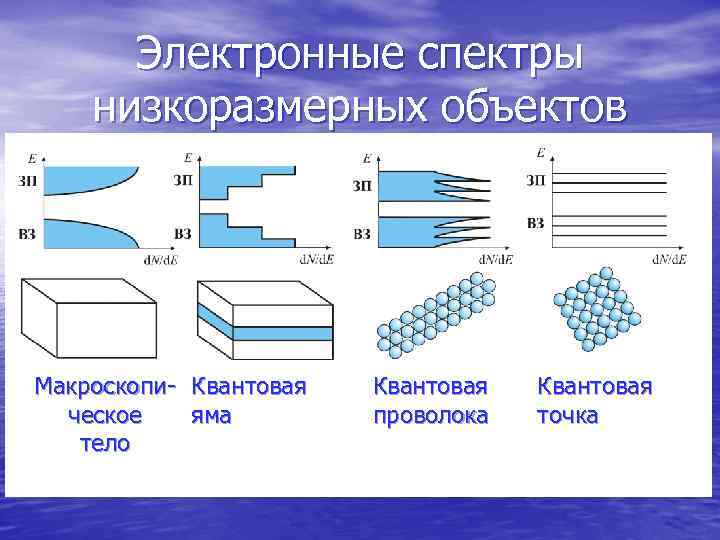
 Электронные спектры низкоразмерных объектов Макроскопи- Квантовая ческое яма проволока точка тело
Электронные спектры низкоразмерных объектов Макроскопи- Квантовая ческое яма проволока точка тело
 Примеры размерных эффектов в химии
Примеры размерных эффектов в химии
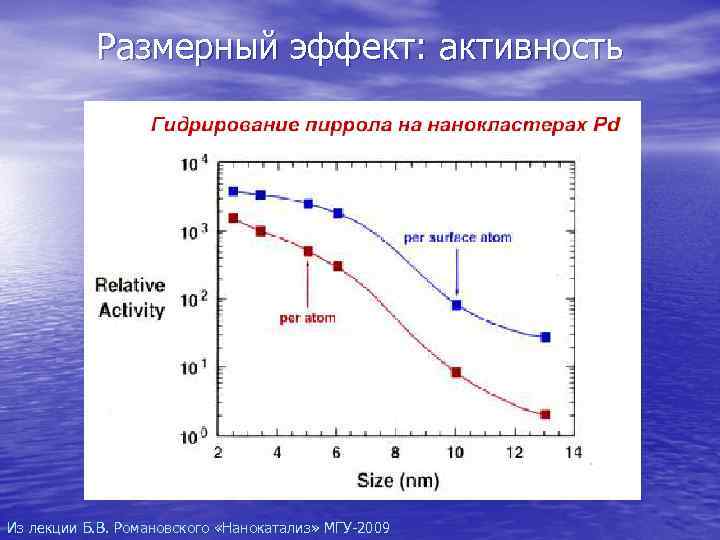
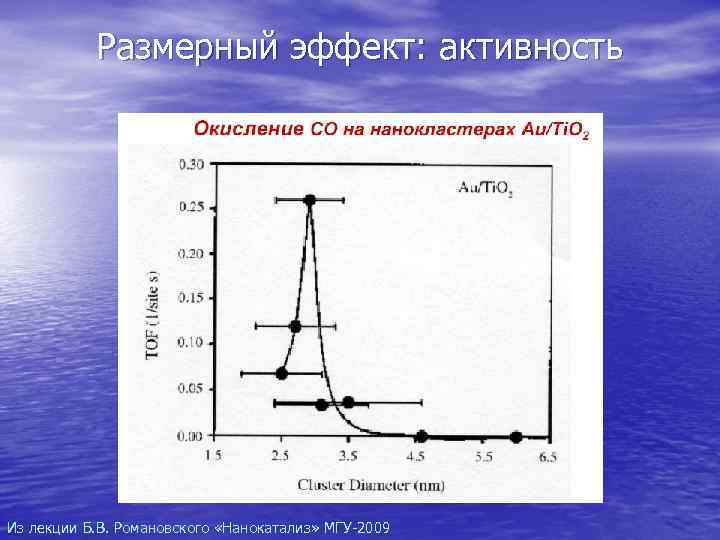
 Размерный эффект: активность Из лекции Б. В. Романовского «Нанокатализ» МГУ-2009
Размерный эффект: активность Из лекции Б. В. Романовского «Нанокатализ» МГУ-2009
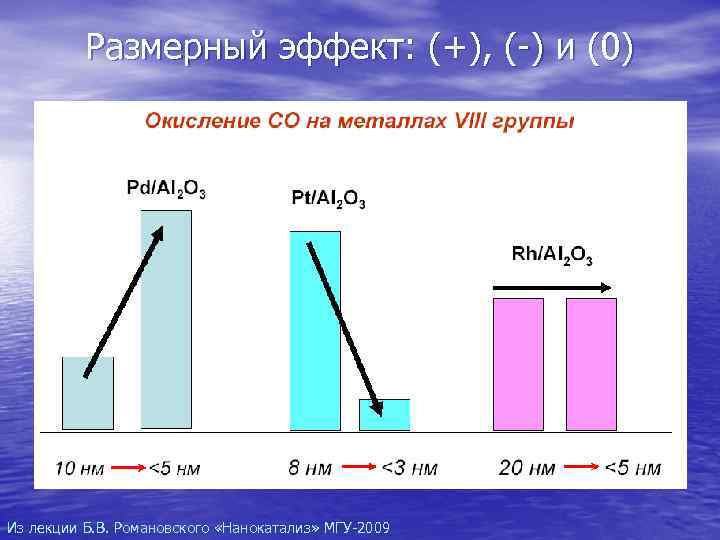
 Размерный эффект: (+), (-) и (0) Из лекции Б. В. Романовского «Нанокатализ» МГУ-2009
Размерный эффект: (+), (-) и (0) Из лекции Б. В. Романовского «Нанокатализ» МГУ-2009
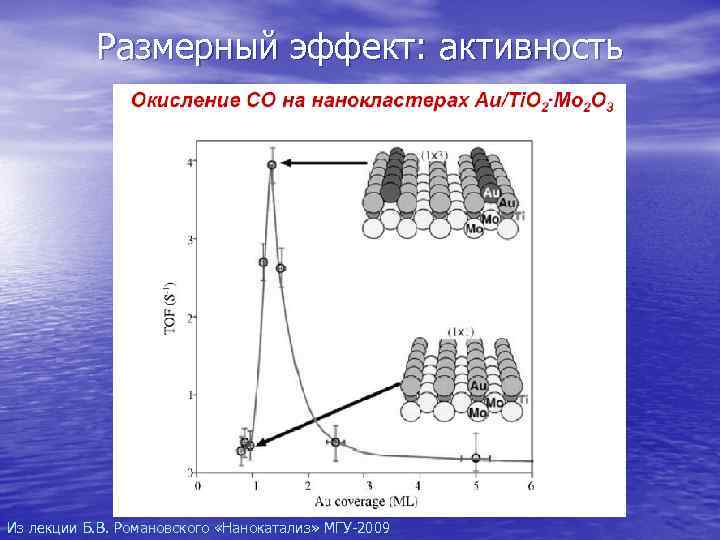
 Размерный эффект: активность Из лекции Б. В. Романовского «Нанокатализ» МГУ-2009
Размерный эффект: активность Из лекции Б. В. Романовского «Нанокатализ» МГУ-2009
 Размерный эффект: активность Из лекции Б. В. Романовского «Нанокатализ» МГУ-2009
Размерный эффект: активность Из лекции Б. В. Романовского «Нанокатализ» МГУ-2009
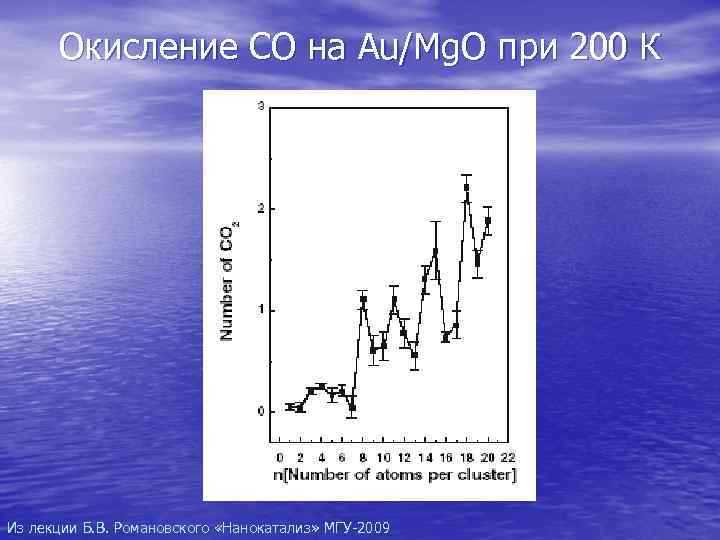
 Окисление CO на Au/Mg. O при 200 К Из лекции Б. В. Романовского «Нанокатализ» МГУ-2009
Окисление CO на Au/Mg. O при 200 К Из лекции Б. В. Романовского «Нанокатализ» МГУ-2009
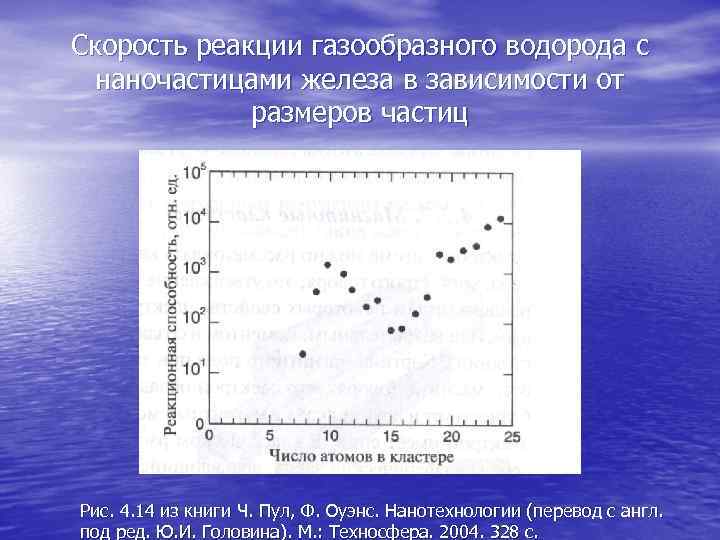
 Скорость реакции газообразного водорода с наночастицами железа в зависимости от размеров частиц Рис. 4. 14 из книги Ч. Пул, Ф. Оуэнс. Нанотехнологии (перевод с англ. под ред. Ю. И. Головина). М. : Техносфера. 2004. 328 с.
Скорость реакции газообразного водорода с наночастицами железа в зависимости от размеров частиц Рис. 4. 14 из книги Ч. Пул, Ф. Оуэнс. Нанотехнологии (перевод с англ. под ред. Ю. И. Головина). М. : Техносфера. 2004. 328 с.
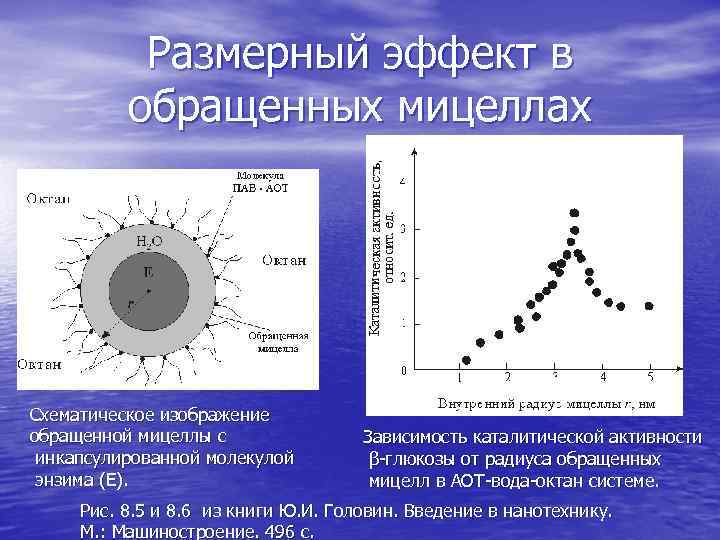
 Размерный эффект в обращенных мицеллах Схематическое изображение обращенной мицеллы с Зависимость каталитической активности инкапсулированной молекулой β-глюкозы от радиуса обращенных энзима (Е). мицелл в АОТ-вода-октан системе. Рис. 8. 5 и 8. 6 из книги Ю. И. Головин. Введение в нанотехнику. М. : Машиностроение. 496 с.
Размерный эффект в обращенных мицеллах Схематическое изображение обращенной мицеллы с Зависимость каталитической активности инкапсулированной молекулой β-глюкозы от радиуса обращенных энзима (Е). мицелл в АОТ-вода-октан системе. Рис. 8. 5 и 8. 6 из книги Ю. И. Головин. Введение в нанотехнику. М. : Машиностроение. 496 с.
 Литература 1. Ч. Пул, Ф. Оуэнс. Нанотехнологии (перевод с англ. под ред. Ю. И. Головина). М. : Техносфера. 2004. 328 с. 2. Ю. И. Головин. Основы нанотехнологий. М. : Машиностроение. 2012. 496 с. 3. Н. Г. Рамбиди, А. В. Березкин. Физические и химические основы нанотехнологии. М. : Физматлит. 2008. 456 с. 4. И. П. Суздалев. Нанотехнологии: физико-химия нанокластеров, наноструктур и наноматериалов. М. : Ком. Книга. 2006. 596 с. 5. Г. Б. Сергеев. Нанохимия. М. : Изд-во МГУ. 2003. 288 с. 6. Р. А. Андриевский, А. В. Рагуля. Наноструктурные материалы. М. : Академия. 2005. 192 с. 7. А. Л. Бучаченко. Нанохимия – прямой путь к высоким технологиям нового века. Успехи химии. 2003. 419 с. 8. Ю. Д. Третьяков, Е. А. Гудилин. Основные направления фундаментальных и ориентированных исследований в области наноматериалов. Успехи химии. 2009. Т. 78. № 9. С. 867 -888.
Литература 1. Ч. Пул, Ф. Оуэнс. Нанотехнологии (перевод с англ. под ред. Ю. И. Головина). М. : Техносфера. 2004. 328 с. 2. Ю. И. Головин. Основы нанотехнологий. М. : Машиностроение. 2012. 496 с. 3. Н. Г. Рамбиди, А. В. Березкин. Физические и химические основы нанотехнологии. М. : Физматлит. 2008. 456 с. 4. И. П. Суздалев. Нанотехнологии: физико-химия нанокластеров, наноструктур и наноматериалов. М. : Ком. Книга. 2006. 596 с. 5. Г. Б. Сергеев. Нанохимия. М. : Изд-во МГУ. 2003. 288 с. 6. Р. А. Андриевский, А. В. Рагуля. Наноструктурные материалы. М. : Академия. 2005. 192 с. 7. А. Л. Бучаченко. Нанохимия – прямой путь к высоким технологиям нового века. Успехи химии. 2003. 419 с. 8. Ю. Д. Третьяков, Е. А. Гудилин. Основные направления фундаментальных и ориентированных исследований в области наноматериалов. Успехи химии. 2009. Т. 78. № 9. С. 867 -888.

