МОДУЛЬ 1 Передача інформації в інформаційних системах Тема

МОДУЛЬ 1 Передача інформації в інформаційних системах Тема 1. Сучасні системи передавання інформації в телекомунікаційних системах 1. 1. Цифрова система передавання дискретних повідомлень 1. 2 Поняття про типові перетворення сигналів у радіотехнічних колах, пристроях, системах 1. 3 Структурна схема системи радіопередавання 1. 4 Перетворення інформації у комп’ютерній мережі

1. 1 ЦИФРОВА СИСТЕМА ПЕРЕДАВАННЯ ДИСКРЕТНИХ ПОВІДОМЛЕНЬ У сучасних телекомунікаційних системах широко використовуються цифрові методи передавання інформації. Інтенсивне впровадження зумовлено перевагами цифрових технологій над аналоговими. Цифрові системи (ЦС) мають більш високу пропускну здатність при умові застосування ефективних методів модуляції, кодування й реалізації оптимальних методів приймання. У ЦС є можливість більш повного використання статистичних характеристик передаваних повідомлень. Подання інформації в універсальній цифровій формі забезпечує велику гнучкість реалізації алгоритмів формування, опрацювання й мультиплексування сигналів, широкі можливості сполучення мереж різних типів. досягнення мікроелектроніки й обчислювальної техніки припускають реалізацію усе більш складних цифрових алгоритмів.

Телекомунікаційна система – складний комплекс, основним завданням якого є передавання інформації із заданою точністю і швидкістю. Основні особливості процесів формування й опрацювання сигналів, що відбуваються в ЦС, розглянуто на прикладі спрощеної структурної схеми, поданої на рис. 1. 1.

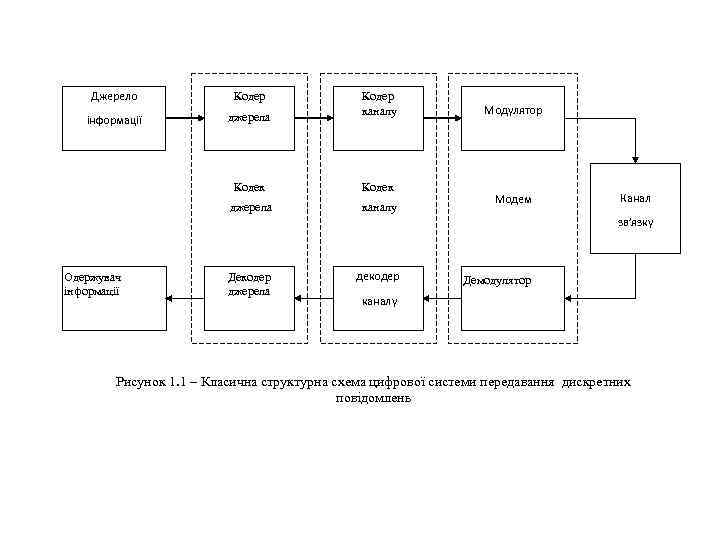Джерело Кодер інформації джерела Кодер каналу Кодек джерела каналу Модулятор Модем Канал зв’язку Одержувач інформації Декодер джерела декодер Демодулятор каналу Рисунок 1. 1 – Класична структурна схема цифрової системи передавання дискретних повідомлень

Джерело інформації формує повідомлення, що підлягають передаванню каналом зв’язку. Це можуть бути послідовності дискретних символів (дані, телеграфні повідомлення) чи неперервні повідомлення (мовлення, телебачення, результати телевимірювань тощо), перетворені в цифрову форму. Реальні повідомлення містять надлишковість, і для їхнього передавання в цифровому вигляді необхідне істотне збільшення пропускної здатності каналу. Для усунення значної частини надлишковості й узгодження джерела інформації з цифровою системою передавання використовується кодер джерела. При кодуванні враховуються статистичні властивості переданих повідомлень, що дозволяє істотно зменшити необхідну швидкість цифрового потоку. Кодер разом з декодером утворюють кодек джерела.

Неперервний канал зв'язку містить у собі лінію зв'язку, передавач і приймач сигналів. У залежності від типу лінії зв'язку (волоконно-оптичний кабель чи кабель з мідними жилами, простір між передавальною і приймальною антенами при використанні радіозв'язку і т. д. ) структура приймально-передавальних пристроїв змінюється. Відмінність прийнятого сигналу від переданого зумовлена дією завад і спотворень у каналі зв’язку. У модуляторі формуються сигнали-переносники, форми яких повинні задовольняти вимогам до завадостійкості, смуги займаних частот, швидкості передавання та стійкості до спотворень у лінії зв'язку. Джерело й одержувач повідомлень оперують, як правило, з двійковими символами, тоді як часто в каналах використовують недвійкові (багатопозіційні) ансамблі сигналів. У цьому разі узгодження первинного сигналу з каналом зв’язку є також функцією модема, до складу якого входить як модулятор, так і демодулятор.

Завадостійке кодування є ефективним засобом підвищення достовірності переданої інформації. Це зумовило широке використання кодів у цифрових телекомунікаційних системах. Можливість виявляти й виправляти помилки в прийнятій інформації виникає за рахунок уведення надлишковості при кодуванні. Відповідно до теорії, можливе є яке завгодно велике підвищення правильності передачі інформації, якщо швидкість надходження інформації від джерела не перевищує пропускної здатності каналу. Досягається це застосуванням досить довгих завадостійких кодів. У реальних умовах довжина коду є обмежена припустимою складністю пристроїв кодування і, насамперед, декодування. Тому основна задача теорії кодування полягає у розробці таких завадостійких кодів, які забезпечують за кінцевої довжини і припустимої надлишковості коду необхідну достовірність передавання.

Сучасні системи передавання інформації, як правило, є багатоканальні, що зумовлює їх поєднання в телекомунікаційні мережі. При цьому виникають проблеми розподілення сигналів різних каналів і множинного доступу різних користувачів до спільних ресурсів мереж. Використання ефективних методів модуляції дозволяє розв’язувати й такі задачі.

1. 2 Поняття про типові перетворення сигналів у радіотехнічних колах, пристроях, системах Типовими перетвореннями сигналів у процесі їх передавання радіоканалами є: - перетворення повідомлення-сигнал (сигнал-повідомлення) – перевагою електричних сигналів є швидкість і дальність їх розповсюдження, але сприйняття електричних сигналів людиною неможливо, окрім того, у багатьох випадках вихідні повідомлення мають не електричну природу, отже, необхідністю є перетворень повідомлення-сигнал (мікрофон, електронно-променева трубка, сканер та інше) і сигналповідомлення (динамік, електронно-променева трубка, принтер та інше); вважається, що зазначені перетворення здійснюються джерелом повідомлення і одержувачем повідомлення; сигнал на виході джерела повідомлення b(t) називається первинним;

ü генерування високочастотних гармонічних коливань – для того, щоб передавати сигнали радіоканалами необхідно перенести їх спектр у смугу пропускання каналу, для чого використовується високочастотне гармонічне коливання, яке називають переносником або несівною; ü модуляція – процес перетворення первинного сигналу у радіосигнал, який придатний для передавання радіоканалами; сигнал на виході модулятора називається вторинним (модульованим); ü підсилення; ü фільтрація; ü детектування (демодуляція) – процес зворотний модуляції, тобто відновлення первинного сигналу з модульованого; цьому процесу заважають завади, що діють у радіоканалі у процесі розповсюдження сигналу; основною завадою у радіоканалах є теплові шуми.

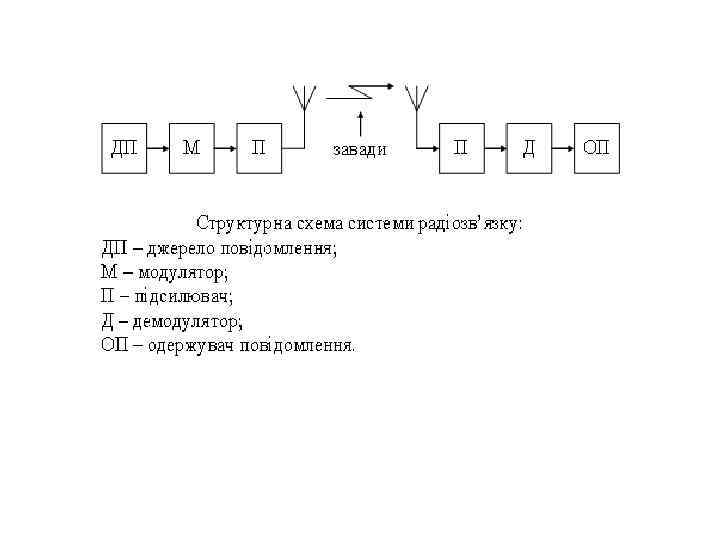
1. 3 Структурна схема системи радіопередавання Системи, в яких радіосигнали формуються, розповсюджуються відкритим повітряним простором та приймаються називаються радіотехнічними системами. Системи радіозв’язку або системи радіопередавання відносяться до радіотехнічних систем, в яких електричні сигнали використовуються для передавання інформації на відстань від джерела до одержувача повідомлення. До радіотехнічних систем також відносяться системи радіолокації, радіонавігації, радіотелеметрії, радіокерування та інші.

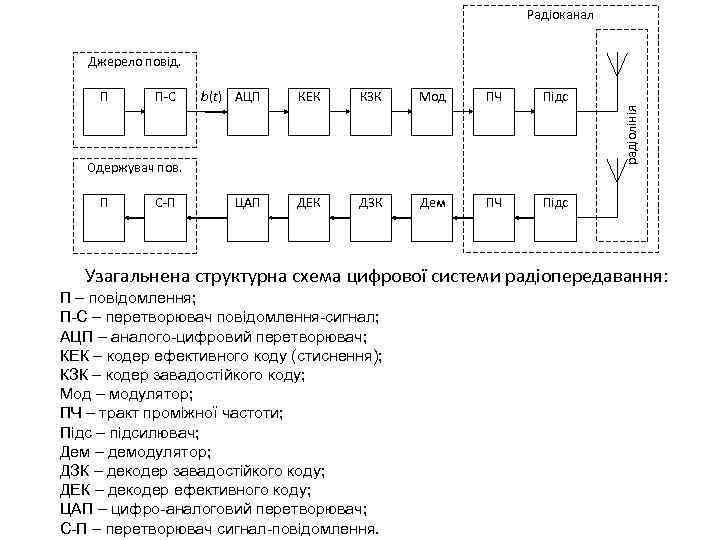Радіоканал Джерело повід. П-С b(t) АЦП КЕК КЗК Мод ПЧ Підс ЦАП ДЕК ДЗК Дем ПЧ Підс радіолінія П Одержувач пов. П С-П Узагальнена структурна схема цифрової системи радіопередавання: П – повідомлення; П-С – перетворювач повідомлення-сигнал; АЦП – аналого-цифровий перетворювач; КЕК – кодер ефективного коду (стиснення); КЗК – кодер завадостійкого коду; Мод – модулятор; ПЧ – тракт проміжної частоти; Підс – підсилювач; Дем – демодулятор; ДЗК – декодер завадостійкого коду; ДЕК – декодер ефективного коду; ЦАП – цифро-аналоговий перетворювач; С-П – перетворювач сигнал-повідомлення.

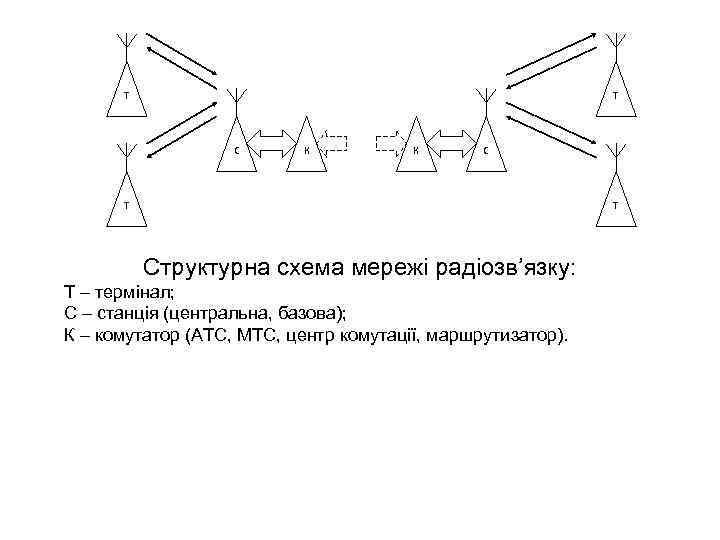Т Т С К К С Т Т Структурна схема мережі радіозв’язку: Т – термінал; С – станція (центральна, базова); К – комутатор (АТС, МТС, центр комутації, маршрутизатор).

Тема 2. Інформаційні характеристики джерел дискретних повідомлень 2. 1. Інформація, повідомлення, сигнал. Інформація – це будь-які відомості, що передаються будьяким чином між джерелом інформації і одержувачем інформації. Інформація це категорія, яка більше відноситься до філософії. Для системи передавання більш корисною є категорія повідомлення – спосіб представлення інформації. Однакова інформація може бути представлена у вигляді: üмовного повідомлення; üвізуального повідомлення; üтекстового повідомлення.

Перераховані види повідомлень є вихідними для будь-якої існуючої системи передачі або системи електрозв’язку. Однак ці види повідомлень не пристосовані для передавання системами електрозв’язку, тому вони перетворюються у особливий вид повідомлення – електричний сигнал. Дискретне джерело інформації – це таке джерело, яке може виробити ( згенерувати ) за скінчений відрізок часу тільки скінчену множину повідомлень. Кожному такому повідомленню можна співставити відповідне число, та передавати ці числа замість повідомлень. Дискретне джерело інформації є достатньо адекватною інформаційною моделлю дискретних систем, а також неперервних систем, інформаційні сигнали про стан яких піддають аналого - цифровому перетворенню; таке перетворення виконується в більшості сучасних автоматизованих систем управління.

Первинні характеристики дискретного джерела інформації – це алфавіт, сукупність ймовірностей появи символів алфавіту на виході дискретного джерела та тривалості символів. Алфавіт – множина символів, які можуть з’явитися на виході дискретного джерела; М – алфавіт джерела, тобто кількість різноманітних символів алфавіту. Якщо всі ймовірності, які визначають виникнення символів на виході джерела, не залежать від часу, джерело називають стаціонарним. Ми будемо розглядати тільки стаціонарні джерела та для скорочення замість “стаціонарне джерело” будемо всюди використовувати “джерело”. Для опису джерел, які не мають пам’яті, достатньо мати значення безумовних імовірностей p(xi) виникнення символів xi , i = 1, 2, 3, …, M на його виході.

Більшість реальних джерел інформації є джерелами з пам’яттю. Розподіл ймовірностей виникнення чергового символу на виході дискретного джерела з пам’яттю залежить від того, які символи були попередніми. Таке джерело інформації називають марковським, оскільки процес появи символів на його виході адекватний ланцюгам Маркова; останні в свою чергу отримали таку назву на честь російського математика Маркова Андрія Андрійовича (1856 – 1922), який заклав основи розділу теорії випадкових процесів. Будемо говорити, що глибина пам’яті марковського дискретного джерела інформації дорівнює h, ( h 0 ), якщо ймовірність появи чергового символу залежить тільки від h попередніх символів на виході цього джерела.

Сигнал – це фізичний процес або явище, що переносить інформацію о будь-якій події або о стані об’єкта спостереження. Якщо фізичним процесом є електричний струм, електрична напруга або напруженість поля електромагнітної хвилі, то сигнал називається електричним. Отже електричні сигнали є переносниками інформації (повідомлень) у радіотехнічних системах.

2. 2. Кількісна міра інформації Кількість інформації – одне із основних понять теорії інформації, яка розглядає технічні аспекти інформаційних проблем, тобто вона дає відповіді на запитання такого типу: якою повинна бути ємність запам’ятовуючого пристрою для запису даних про стан деякої системи, якими повинні бути характеристики каналу зв’язку для передачі певного повідомлення тощо.

Кількість інформації I (ak), дв. од. , у повідомленні ak з імовірністю його появи P(ak), обчислюється як I(ak) = – log 2 P(ak) Ентропія джерела H(A), це – середня кількість інформації в одному повідомленні. Для М незалежних повідомлень обчислюється як математичне сподівання

Ентропія, як і інформація, завжди додатна й досягає максимального значення Hmax (А) = log 2 M. Надмірність (надлишковість) джерела характеризує зменшення ентропії джерела в порівнянні з максимальним значенням внаслідок того, що деякі з повідомлень несуть малу (а то і нульову) кількість інформації. Кількісно надмірність оцінюється коефіцієнтом Кн, що називається коефіцієнтом надмірності і визначається за формулою

Продуктивність джерела, Rдж, біт/с – це середня кількість інформації, що видається джерелом за одиницю часу Rдж = Н(А)/ Тсер де Тсер – середня тривалість одного повідомлення джерела.

2. 3 Математична модель двох джерел дискретних повідомлень та її статистичні характеристики. Математична модель двох джерел. За термінологією два стаціонарні джерела A та B мають об’єднаний ансамбль AB і видають дискретні повідомлення аk та bk.

Статистичні характеристики двох джерел повідомлень такі: – апріорна (безумовна) імовірність повідомлень аk та bk – P(аk) та P(bk); – апостеріорна (умовна) імовірність повідомлення аk джерела A, якщо має місце повідомлення bk джерела B – P(аk/bk) ; – спільна ймовірність повідомлень аk та bk – P(аk, bk) = P(аk)P(bk/ak) = = P(bk)P(ak/bk); – Tзн – тривалістю видачі повідомлення аk чи bk джерелом.

Типовим прикладом двох джерел повідомлень є повідомлення від якогось джерела A на вході каналу зв’язку та ті ж самі повідомлення на виході каналу. Ми спостерігаємо повідомлення на виході каналу (джерело B), а інформацію маємо отримати про джерело A. Кількість інформації в повідомленні аk чи bk об’єднаного ансамблю AB двох джерел повідомлень A i B характеризується умовною та спільною інформацією. Умовна кількість інформації в повідомленні аk чи bk об’єднаного ансамблю AB двох джерел дискретних повідомлень A i B і(аk/bk), визначається: і(аk/bk) = – log 2 P(аk/bk) і(bk/ak) = – log 2 P(bk/ak) [дв. од. ]

Спільна кількість інформації в повідомленнях аk та bk об’єднаного ансамблю AB двох джерел повідомлень A та B – і(аk, bk) чи і(bk, ak), визначається: і(аk, bk) = – log 2 P(аk, bk) і(bk. ak) = – log 2 P(bk. ak) [дв. од. ]

Середня кількість інформації об’єднаного ансамблю AB двох джерел повідомлень A та B характеризується умовною, спільною та взаємною ентропіями. Умовна ентропія – середня кількість інформації, яку переносить одне повідомлення джерела при залежних повідомленнях. Умовна ентропія двох джерел повідомлень A i B чи B і A, визначається: Н (A/B) = M (і(аk/bk))

Спільна ентропія – середня кількість інформації, яку переносять повідомлення джерел A та B з врахуванням статистичної залежності між ними. Спільна ентропія об’єднаного ансамблю AB двох джерел повідомлень A та B, визначається: Нсп (AB) = Н(A) + Нум (B/A) = = Н(B) + Нум (A/B) [дв. од. /пов. (біт/пов. )]

Взаємна ентропія об’єднаного ансамблю AB двох джерел повідомлень показує середню кількість інформації, яку можна отримати про джерело А, спостерігаючи джерело В. Взаємна ентропія об’єднаного ансамблю AB двох джерел повідомлень A та B, визначається: Нвз (A, B) = Н(A) – Нум (A/B) = = Н(B) – Нум (B/A) [дв. од. /пов. (біт/пов. )]

Продуктивність об’єднаного ансамблю AB двох джерел повідомлень A та B, визначається: Rдж (A, B) = Нсп (A, B) /Тср [дв. од. /с (біт/с)] Швидкість передачі інформації між двома джерелами повідомлень A та B, визначається: R (A→B) = Нвз (A, B) /Тср [дв. од. /с (біт/с)]

2. 4 Ентропія джерела залежних повідомлень. Користуючись поняттям умовної ентропії, можна отримати вираз для обчислення ентропії Нп(X) джерела з пам’яттю, яке має алфавіт X. Якщо глибина пам’яті такого джерела дорівнює h, а потужність алфавіту M, то можна вважати, що перед генерацією чергового символу джерело знаходиться в одному з Q=Mh станів, де під станом розуміємо одну з можливих послідовностей попередніх символів довжиною h на його виході.

Тоді частинна умовна ентропія H (X/s) при умові, що джерело перебуває в s-му стані де p(xi/s) – умовна ймовірність появи символу xi, якщо джерело перебуває в s-му стані. Усереднюючи H (X/s) по усіх станах, отримаємо вираз для ентропії марковського джерела: p(s) – ймовірність перебування джерела в s-му стані.

Для джерела з глибиною пам’яті h = 2 стан визначається парою символів (xi, xj), а ентропія: Аналогічно можна отримати вирази для ентропій марковських джерел при більш глибоких статистичних зв’язках. Отже, за наявності зв'язку між елементарними повідомленнями ентропія джерела знижується, причому в тим більшому ступені, чим сильніше зв'язок між елементами повідомлення.

Таким чином, можна зробити наступні висновки щодо ступеня інформативності джерел повідомлень: 1. Ентропія джерела і кількість інформації тим більше, чим більше розмір алфавіту джерела. 2. Ентропія джерела залежить від статистичних властивостей повідомлень. Ентропія максимальна, якщо повідомлення джерела рівноімовірні і статистично незалежні. 3. Ентропія джерела, що виробляє нерівноімовірні повідомлення, завжди менше за максимально досяжну. 4. За наявності статистичних зв'язків між елементарними повідомленнями (пам'яті джерела) його ентропія зменшується.

Як приклад розглянемо джерело з алфавітом, що складається з літер А={а, б, в, . . . , ю, я}. Вважатимемо для простоти, що розмір алфавіту джерела = 25 = 32. Якби всі літери алфавіту мали однакову імовірність і були статистично незалежні, то середня ентропія, що доводиться на один символ, склала б H max(А) = log 2 32 = 5 біт/літеру. Якщо тепер врахувати лише різну імовірність літер в тексті (а неважко перевірити, що так воно і є), розрахункова ентропія складе H(А) = 4, 39 біт/літеру.

З урахуванням кореляції (статистичного зв'язку) між двома і трьома сусідніми літерами (після літери “П” частіше зустрічається “A” і майже ніколи – “Ю” і “Ц”) ентропія зменшиться, відповідно, до H(А) = 3, 52 біт/літеру і H (А) = 3, 05 біт/літеру. Якщо врахувати кореляцію між вісьма і більш символами, ентропія зменшиться до H(А) = 2, 0 біт/літеру і далі залишається без змін.

Реальні джерела з одним і тим же розміром алфавіту можуть мати абсолютно різну ентропію. Наприклад надмірність літературного російського тексту складе К= 1 - ( 2 біт/літеру )/( 5 біт/літеру ) = 0, 6. Іншими словами, при передаванні тексту по каналу зв'язку кожні шість букв з десяти переданих не несуть ніякої інформації і можуть без жодних втрат просто не передаватися.

Виникає питання: чи можна не займати носій інформації або канал зв'язку передачею символів, які практично не несуть інформації, або ж можливе таке перетворення вихідного повідомлення, при якому інформація скорочувалася б в мінімально необхідне для цього число символів? Таке можливе і необхідне. Сьогодні системи передачі інформації і зв'язку просто не змогли би працювати, якби в них не використовувалось такого роду кодування. Не було б цифрового стільникового. Не працювали б системи цифрового супутникового телебачення, дуже неефективною була б робота Internet, не було б можливості подивитися відеофільм або послухати музику з лазерного диска. Все це забезпечується ефективним або економним кодуванням інформації в даних системах.