32aa49bdcb190da3f4432a0c709bb0a7.ppt
- Количество слайдов: 33
 Models of the Solar System • Positions of planets change, whereas stars appear relatively ‘fixed’ • Greeks held on to the Geocentric model because they could not observe stars to change their positions, and therefore thought that the earth must be stationary • Ptolemy, Aristotle and others refined the geocentric model • But there were problems……. such as the path reversal by Mars Retrograde motion
Models of the Solar System • Positions of planets change, whereas stars appear relatively ‘fixed’ • Greeks held on to the Geocentric model because they could not observe stars to change their positions, and therefore thought that the earth must be stationary • Ptolemy, Aristotle and others refined the geocentric model • But there were problems……. such as the path reversal by Mars Retrograde motion
 Retrograde motion of Mars (path reversal seen in the Sky)
Retrograde motion of Mars (path reversal seen in the Sky)
 Epicycles – Ptolemic Geocentric Model
Epicycles – Ptolemic Geocentric Model
 How do we know the Earth is spherical ? • The ancient Greeks had deduced not only that the Earth is spherical but also measured its circumference ! • What kind of an object always has a round shadow ?
How do we know the Earth is spherical ? • The ancient Greeks had deduced not only that the Earth is spherical but also measured its circumference ! • What kind of an object always has a round shadow ?
 Earth Shadow during Lunar Eclipse Multiple Exposure Photograph
Earth Shadow during Lunar Eclipse Multiple Exposure Photograph
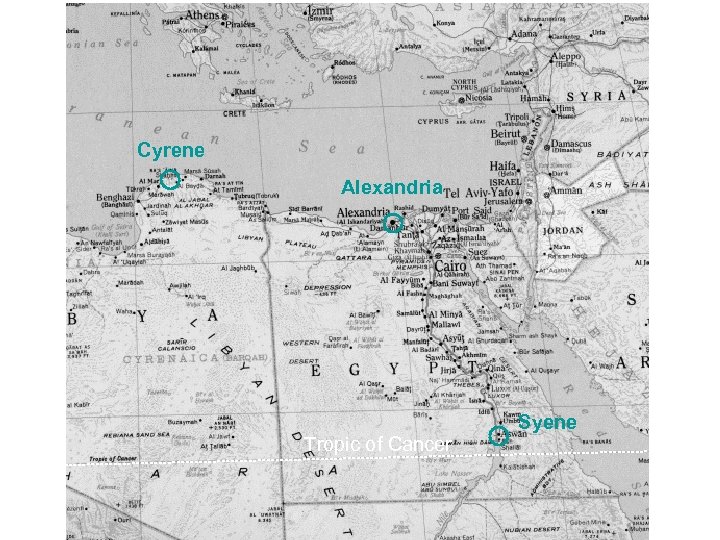 Cyrene Alexandria Tropic of Cancer Syene
Cyrene Alexandria Tropic of Cancer Syene
 Eratosthenes’s method to measure the circumference of the earth At noon on summer solstice day the Sun is directly overhead at Syene, but at an angle of 7 o at Alexandria 7º 7 = Distance (Alexandria - Syene) --------------------360 Circumference of the Earth Sunlight Alexandria Answer: 40, 000 stadia = 25, 000 mi ! Syene Earth
Eratosthenes’s method to measure the circumference of the earth At noon on summer solstice day the Sun is directly overhead at Syene, but at an angle of 7 o at Alexandria 7º 7 = Distance (Alexandria - Syene) --------------------360 Circumference of the Earth Sunlight Alexandria Answer: 40, 000 stadia = 25, 000 mi ! Syene Earth
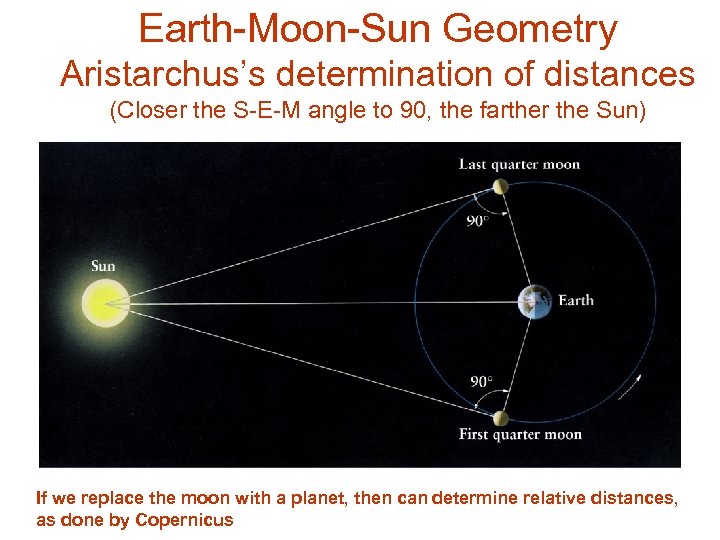 Earth-Moon-Sun Geometry Aristarchus’s determination of distances (Closer the S-E-M angle to 90, the farther the Sun) If we replace the moon with a planet, then can determine relative distances, as done by Copernicus
Earth-Moon-Sun Geometry Aristarchus’s determination of distances (Closer the S-E-M angle to 90, the farther the Sun) If we replace the moon with a planet, then can determine relative distances, as done by Copernicus
 Copernicus
Copernicus
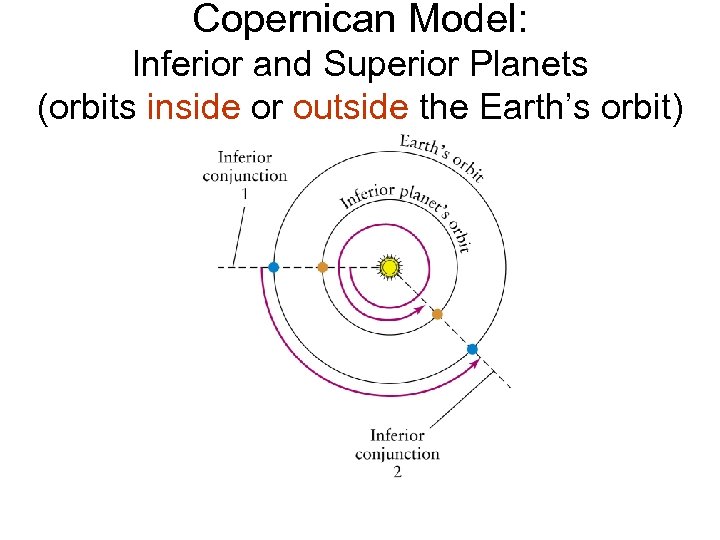 Copernican Model: Inferior and Superior Planets (orbits inside or outside the Earth’s orbit)
Copernican Model: Inferior and Superior Planets (orbits inside or outside the Earth’s orbit)
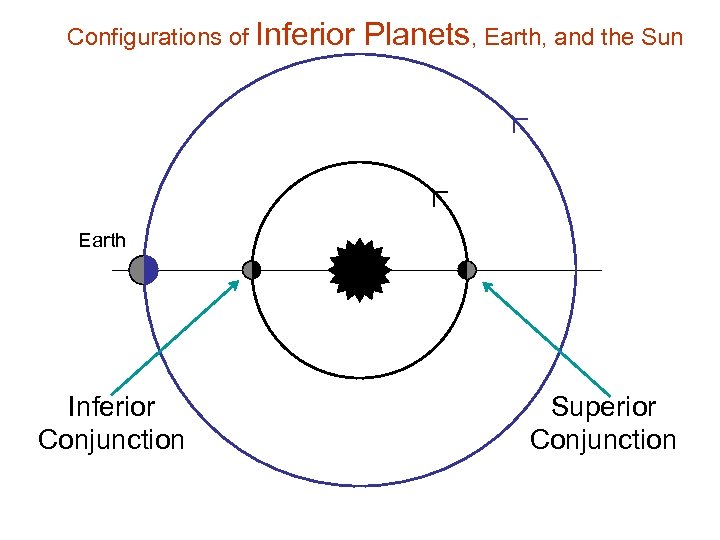 Configurations of Inferior Planets, Earth, and the Sun Earth Inferior Conjunction Superior Conjunction
Configurations of Inferior Planets, Earth, and the Sun Earth Inferior Conjunction Superior Conjunction
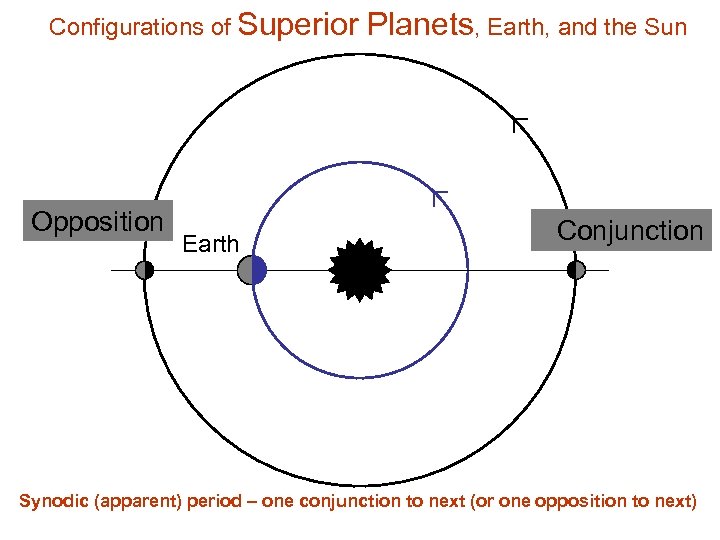 Configurations of Superior Opposition Earth Planets, Earth, and the Sun Conjunction Synodic (apparent) period – one conjunction to next (or one opposition to next)
Configurations of Superior Opposition Earth Planets, Earth, and the Sun Conjunction Synodic (apparent) period – one conjunction to next (or one opposition to next)
 Synodic and Sidereal Orbital Periods • Inferior planets are never at opposition; superior planets can not be at inferior conjunction • Copernican model of orbital periods • Synodic period is the apparent orbital period of a planet, viewed from the earth, when the earth-planet-sun are in successive conjunction or opposition • Sidereal (with respect to stars) period is the real orbital period around the Sun • Synodic periods of outer planets (except Mars) are just over one year
Synodic and Sidereal Orbital Periods • Inferior planets are never at opposition; superior planets can not be at inferior conjunction • Copernican model of orbital periods • Synodic period is the apparent orbital period of a planet, viewed from the earth, when the earth-planet-sun are in successive conjunction or opposition • Sidereal (with respect to stars) period is the real orbital period around the Sun • Synodic periods of outer planets (except Mars) are just over one year
 Apparent (Synodic) and true (Sidereal – with respect to stars) orbital periods of planets differ due to Earth’s relative motion Synodic periods of all outer planets (except mars) are just over 1 year because their Sidereal periods are very long and they are in opposition again soon after an earth-year
Apparent (Synodic) and true (Sidereal – with respect to stars) orbital periods of planets differ due to Earth’s relative motion Synodic periods of all outer planets (except mars) are just over 1 year because their Sidereal periods are very long and they are in opposition again soon after an earth-year
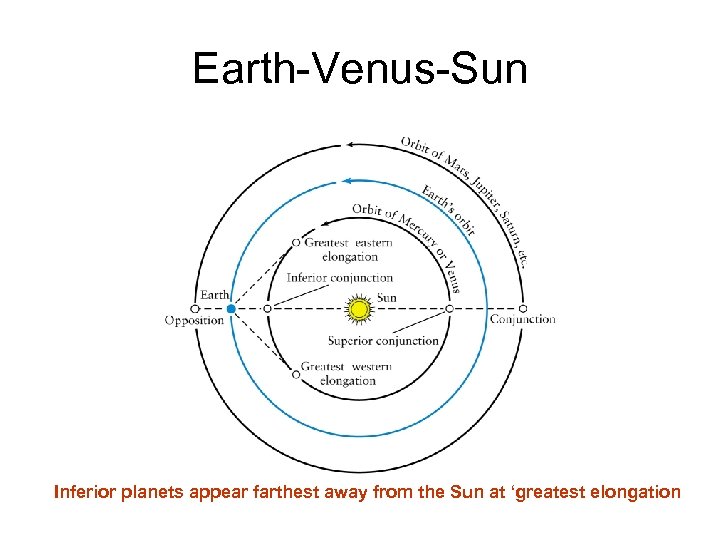 Earth-Venus-Sun Inferior planets appear farthest away from the Sun at ‘greatest elongation
Earth-Venus-Sun Inferior planets appear farthest away from the Sun at ‘greatest elongation
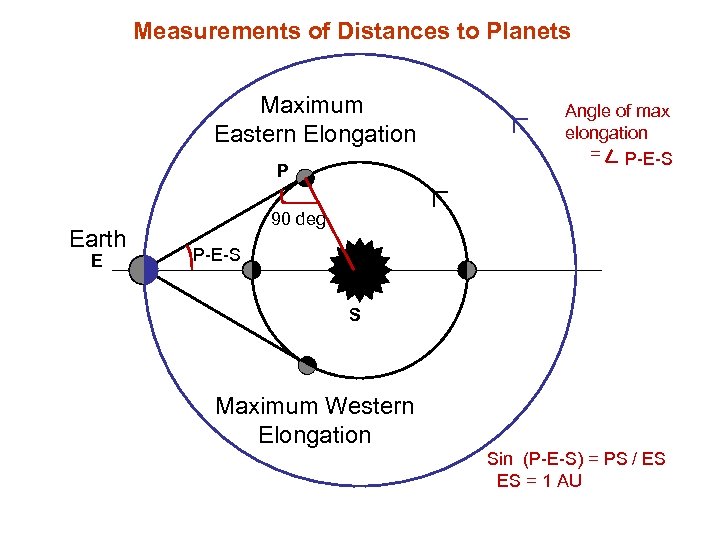 Measurements of Distances to Planets Maximum Eastern Elongation P Earth E Angle of max elongation = P-E-S 90 deg P-E-S S Maximum Western Elongation Sin (P-E-S) = PS / ES ES = 1 AU
Measurements of Distances to Planets Maximum Eastern Elongation P Earth E Angle of max elongation = P-E-S 90 deg P-E-S S Maximum Western Elongation Sin (P-E-S) = PS / ES ES = 1 AU
 Copernicus first determined the relative distances of planets
Copernicus first determined the relative distances of planets
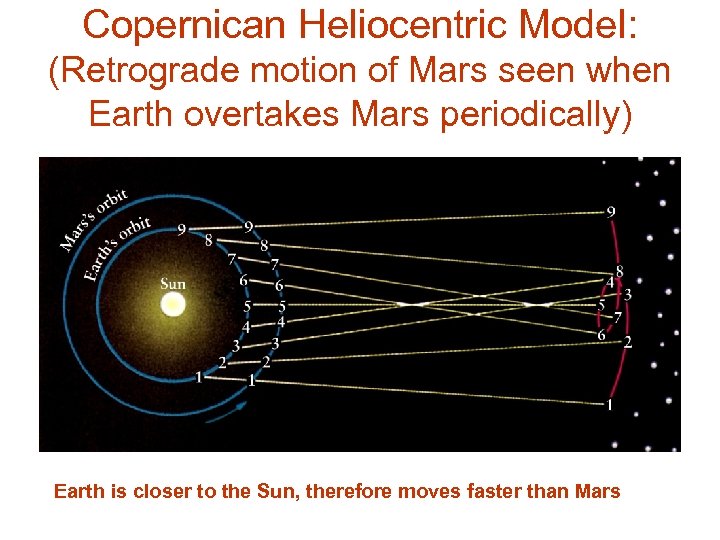 Copernican Heliocentric Model: (Retrograde motion of Mars seen when Earth overtakes Mars periodically) Earth is closer to the Sun, therefore moves faster than Mars
Copernican Heliocentric Model: (Retrograde motion of Mars seen when Earth overtakes Mars periodically) Earth is closer to the Sun, therefore moves faster than Mars
 Tycho: The most accurate pre-telescopic observer Tycho charted very accurately the movement of Mars in the Sky, but still believed In the Geocentric Universe
Tycho: The most accurate pre-telescopic observer Tycho charted very accurately the movement of Mars in the Sky, but still believed In the Geocentric Universe
 Kepler – Tycho’s assistant (used Tycho’s data to derive Kepler’s Laws)
Kepler – Tycho’s assistant (used Tycho’s data to derive Kepler’s Laws)
 Planetary Orbits • The Copernican heliocentric model is essentially correct • But it consisted of circular orbits which did not exactly fit observations of planetary positions • Kepler realized, based on Tycho’s data of the orbit of Mars, that orbits are elliptical Kepler’s First Law • However, the difference for Mars is tiny, to within the accuracy of drawing a circle with a thick pen !
Planetary Orbits • The Copernican heliocentric model is essentially correct • But it consisted of circular orbits which did not exactly fit observations of planetary positions • Kepler realized, based on Tycho’s data of the orbit of Mars, that orbits are elliptical Kepler’s First Law • However, the difference for Mars is tiny, to within the accuracy of drawing a circle with a thick pen !
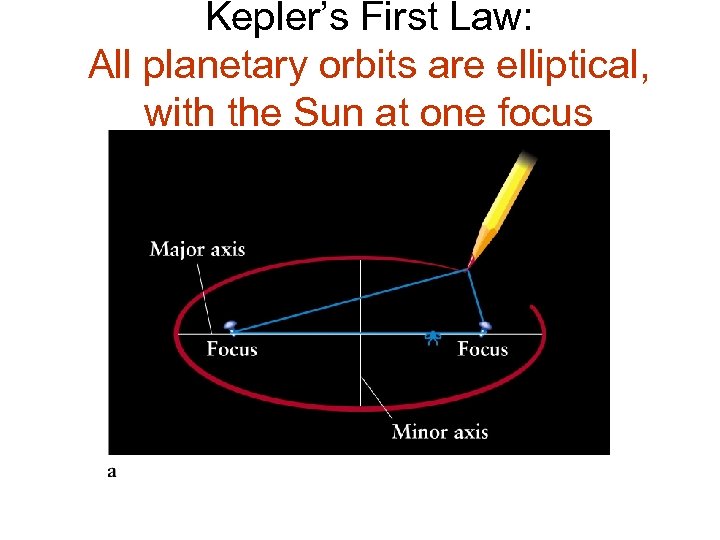 Kepler’s First Law: All planetary orbits are elliptical, with the Sun at one focus
Kepler’s First Law: All planetary orbits are elliptical, with the Sun at one focus
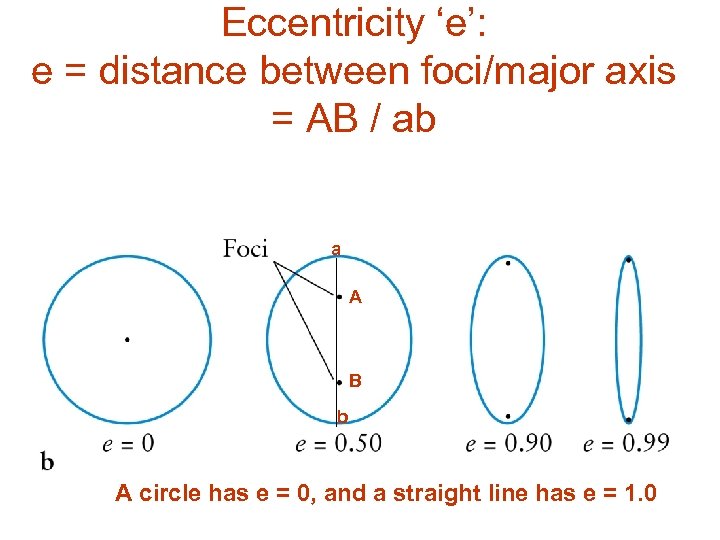 Eccentricity ‘e’: e = distance between foci/major axis = AB / ab a A B b A circle has e = 0, and a straight line has e = 1. 0
Eccentricity ‘e’: e = distance between foci/major axis = AB / ab a A B b A circle has e = 0, and a straight line has e = 1. 0
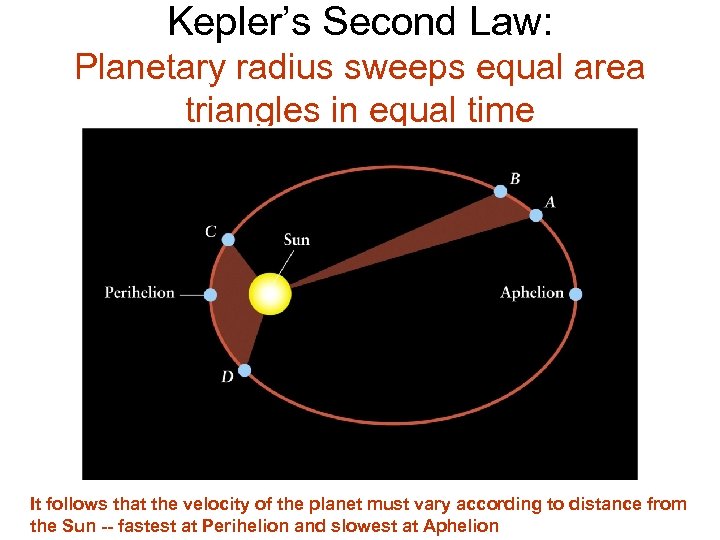 Kepler’s Second Law: Planetary radius sweeps equal area triangles in equal time It follows that the velocity of the planet must vary according to distance from the Sun -- fastest at Perihelion and slowest at Aphelion
Kepler’s Second Law: Planetary radius sweeps equal area triangles in equal time It follows that the velocity of the planet must vary according to distance from the Sun -- fastest at Perihelion and slowest at Aphelion
 Kepler’s Third Law: P 2 = a 3 P – Orbital Period, a – semi-major axis What is the size ‘a’ of the orbit of a comet with the period ‘P’ of 8 years?
Kepler’s Third Law: P 2 = a 3 P – Orbital Period, a – semi-major axis What is the size ‘a’ of the orbit of a comet with the period ‘P’ of 8 years?
 Kepler’s Laws • Empirically derived from observational data largely from Tycho (e. g. observations of the positions of Mars in its orbit around the Sun) • Theoretical explanation had to await Newton’s discovery of the Law of Gravitation • Universally valid for all gravitationally orbiting objects (e. g. stars around black holes before falling in)
Kepler’s Laws • Empirically derived from observational data largely from Tycho (e. g. observations of the positions of Mars in its orbit around the Sun) • Theoretical explanation had to await Newton’s discovery of the Law of Gravitation • Universally valid for all gravitationally orbiting objects (e. g. stars around black holes before falling in)
 Galileo
Galileo
 Galileo’s Discoveries With Telescope • Phases of Venus - Venus displays phases like the Moon as it revolves around the Sun • Mountains and “seas” on the Moon - Other objects in the sky are like the Earth (not therefore special) • Milky Way is made of stars like the Sun • Sunspots - “Imperfections” or “blemishes” in otherwise perfect “heavenly” objects • 4 Galilean satellites of Jupiter - Objects in the sky revolve around other objects, not the Earth (i. e. other moons) All of these supported the Copernican System Galileo also conducted experiments on gravity : Regardless of mass or weight objects fall at the same rate
Galileo’s Discoveries With Telescope • Phases of Venus - Venus displays phases like the Moon as it revolves around the Sun • Mountains and “seas” on the Moon - Other objects in the sky are like the Earth (not therefore special) • Milky Way is made of stars like the Sun • Sunspots - “Imperfections” or “blemishes” in otherwise perfect “heavenly” objects • 4 Galilean satellites of Jupiter - Objects in the sky revolve around other objects, not the Earth (i. e. other moons) All of these supported the Copernican System Galileo also conducted experiments on gravity : Regardless of mass or weight objects fall at the same rate
 Phases of Venus is never too far from the Sun, therefore can not be in opposition like the Moon. Changing phases of Venus demonstrate that it orbits the Sun like the Earth.
Phases of Venus is never too far from the Sun, therefore can not be in opposition like the Moon. Changing phases of Venus demonstrate that it orbits the Sun like the Earth.
 Orbits and Motions • Orbits can not be circular since objects do NOT revolve around each other, but around their common center-of-mass • The Earth and the Moon both revolve around each other • This motion is in addition to Earth’s Rotation, Revolution, Precession
Orbits and Motions • Orbits can not be circular since objects do NOT revolve around each other, but around their common center-of-mass • The Earth and the Moon both revolve around each other • This motion is in addition to Earth’s Rotation, Revolution, Precession
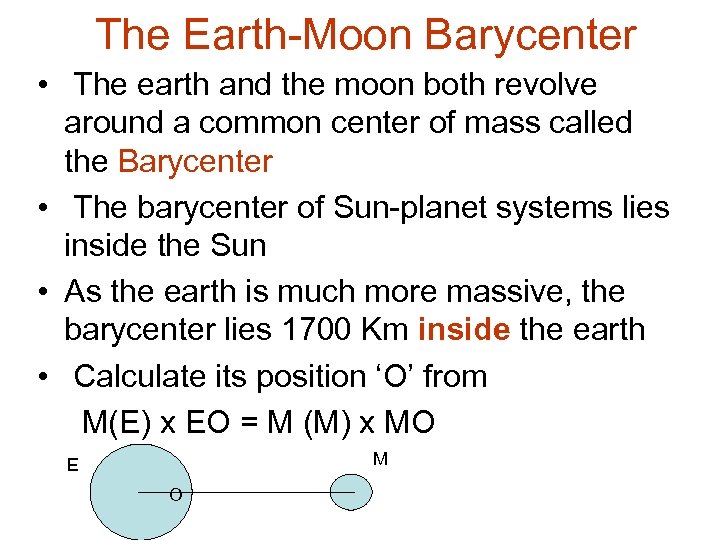 The Earth-Moon Barycenter • The earth and the moon both revolve around a common center of mass called the Barycenter • The barycenter of Sun-planet systems lies inside the Sun • As the earth is much more massive, the barycenter lies 1700 Km inside the earth • Calculate its position ‘O’ from M(E) x EO = M (M) x MO M E O
The Earth-Moon Barycenter • The earth and the moon both revolve around a common center of mass called the Barycenter • The barycenter of Sun-planet systems lies inside the Sun • As the earth is much more massive, the barycenter lies 1700 Km inside the earth • Calculate its position ‘O’ from M(E) x EO = M (M) x MO M E O
 Gravity • Galileo’s observations on gravity led to Newton’s Law of Gravitation and the three Laws of Motion • Objects fall at the same rate regardless of mass because more massive objects have more inertia or resistance to motion • Fgrav = G (m 1 x m 2) / r 2 • Force of gravity between two masses is proportional to the product of masses divided by distance squared ‘inverse square law’
Gravity • Galileo’s observations on gravity led to Newton’s Law of Gravitation and the three Laws of Motion • Objects fall at the same rate regardless of mass because more massive objects have more inertia or resistance to motion • Fgrav = G (m 1 x m 2) / r 2 • Force of gravity between two masses is proportional to the product of masses divided by distance squared ‘inverse square law’
