c6fe9c1b11f0081c526594e7f5c70b40.ppt
- Количество слайдов: 73

Modelling Volatility Skews Bruno Dupire Bloomberg bdupire@bloomberg. net London, November 17, 2006 Bruno Dupire

OUTLINE 1. 2. 3. 4. 5. 6. Bruno Dupire Generalities Leverage and jumps Break-even volatilities Volatility models Forward Skew Smile arbitrage

I. Bruno Dupire Generalities
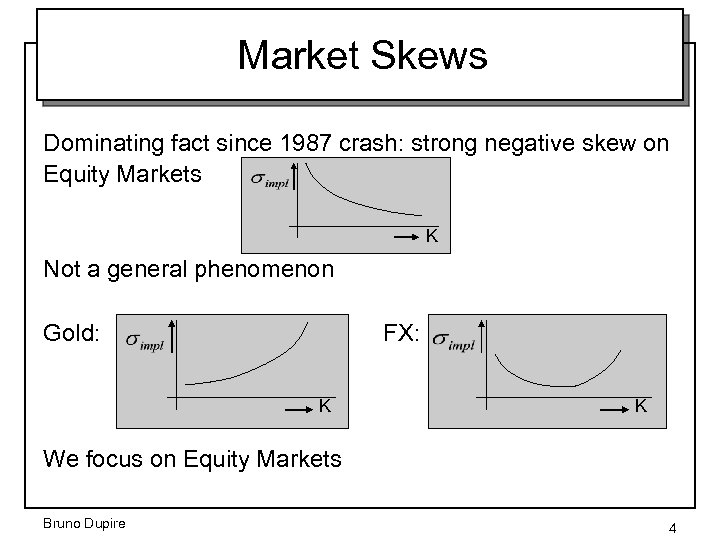
Market Skews Dominating fact since 1987 crash: strong negative skew on Equity Markets K Not a general phenomenon Gold: FX: K K We focus on Equity Markets Bruno Dupire 4
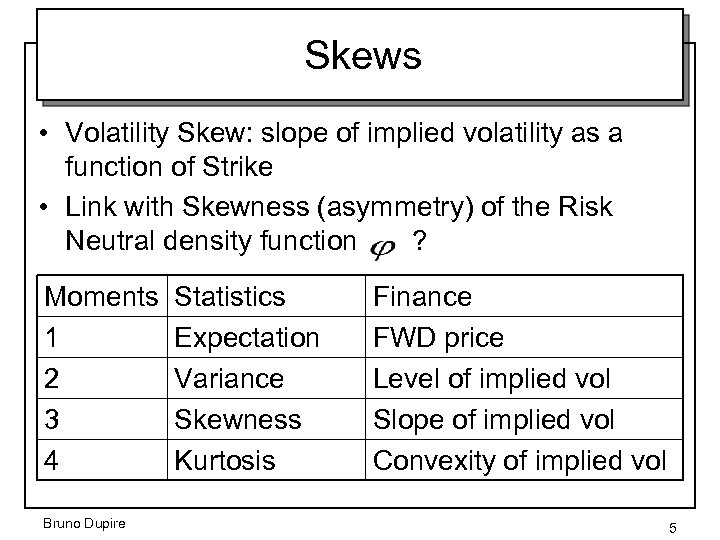
Skews • Volatility Skew: slope of implied volatility as a function of Strike • Link with Skewness (asymmetry) of the Risk Neutral density function ? Moments 1 2 3 4 Bruno Dupire Statistics Expectation Variance Skewness Kurtosis Finance FWD price Level of implied vol Slope of implied vol Convexity of implied vol 5

Why Volatility Skews? • Market prices governed by – a) Anticipated dynamics (future behavior of volatility or jumps) – b) Supply and Demand Sup p ly an Market Skew d De Th. Skew man d K • To “ arbitrage” European options, estimate a) to capture risk premium b) • To “arbitrage” (or correctly price) exotics, find Risk Neutral dynamics calibrated to the market Bruno Dupire 6
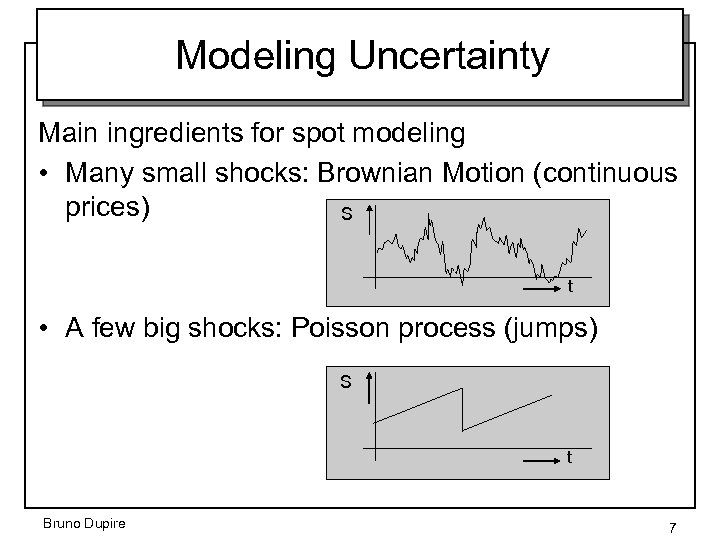
Modeling Uncertainty Main ingredients for spot modeling • Many small shocks: Brownian Motion (continuous prices) S t • A few big shocks: Poisson process (jumps) S t Bruno Dupire 7

2 mechanisms to produce Skews (1) • To obtain downward sloping implied volatilities K – a) Negative link between prices and volatility • Deterministic dependency (Local Volatility Model) • Or negative correlation (Stochastic volatility Model) – b) Downward jumps Bruno Dupire 8
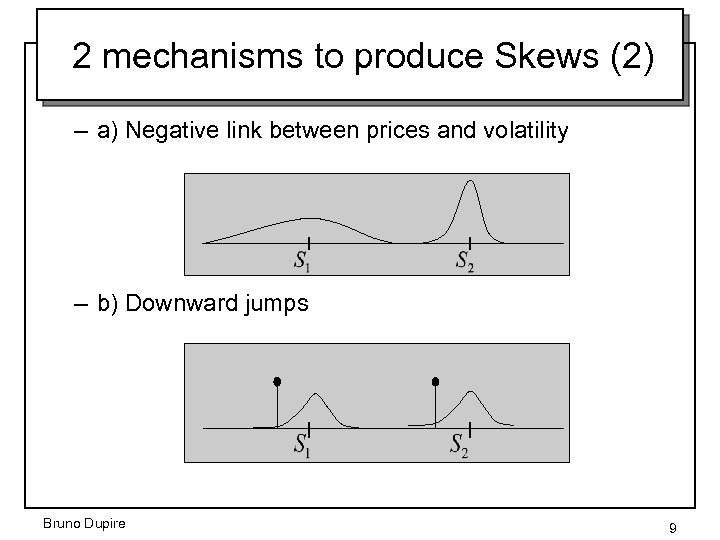
2 mechanisms to produce Skews (2) – a) Negative link between prices and volatility – b) Downward jumps Bruno Dupire 9

Leverage and Jumps Bruno Dupire

Dissociating Jump & Leverage effects t 0 t 1 x = St 1 -St 0 • t 2 y = St 2 -St 1 Variance : FWD variance Option prices Δ Hedge • Skewness : Leverage Option prices Δ Hedge Bruno Dupire FWD skewness 11

Dissociating Jump & Leverage effects Define a time window to calculate effects from jumps and Leverage. For example, take close prices for 3 months • Jump: • Leverage: Bruno Dupire 12

Dissociating Jump & Leverage effects Bruno Dupire 13

Dissociating Jump & Leverage effects Bruno Dupire 14

Break Even Volatilities Bruno Dupire
Theoretical Skew from Prices ? => Problem : How to compute option prices on an underlying without options? For instance : compute 3 month 5% OTM Call from price history only. 1) Discounted average of the historical Intrinsic Values. 2) Bad : depends on bull/bear, no call/put parity. 2) Generate paths by sampling 1 day return recentered histogram. 3) Problem : CLT => converges quickly to same volatility for all strike/maturity; breaks autocorrelation and vol/spot dependency. Bruno Dupire 16
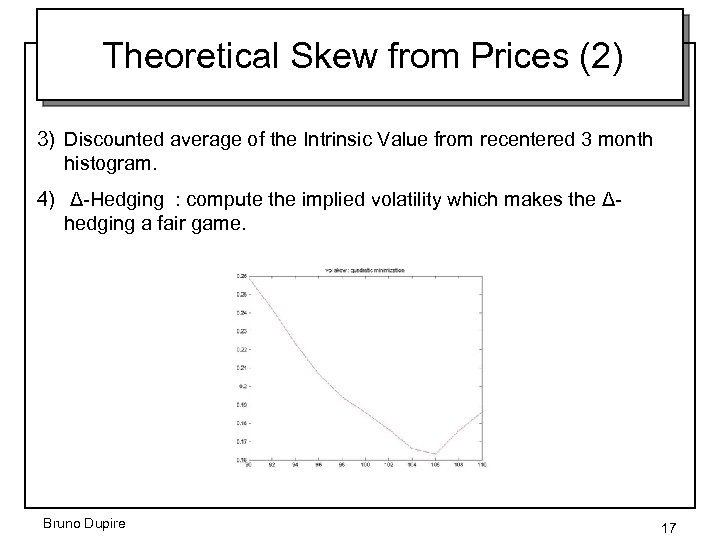
Theoretical Skew from Prices (2) 3) Discounted average of the Intrinsic Value from recentered 3 month histogram. 4) Δ-Hedging : compute the implied volatility which makes the Δhedging a fair game. Bruno Dupire 17
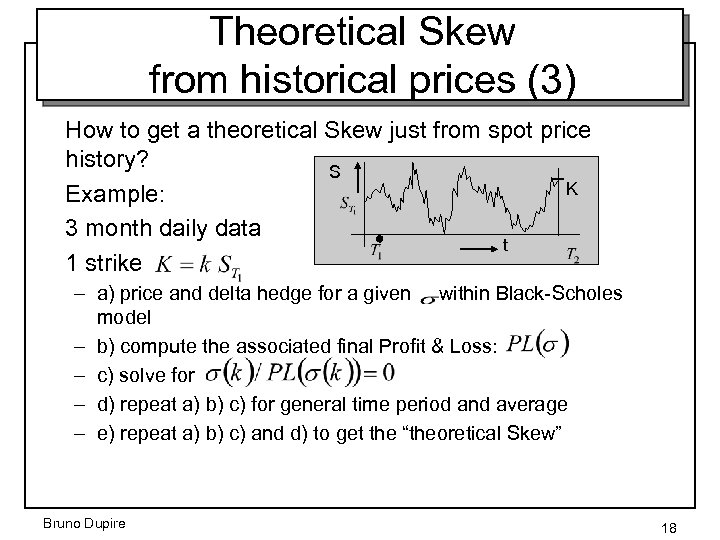
Theoretical Skew from historical prices (3) How to get a theoretical Skew just from spot price history? S K Example: 3 month daily data t 1 strike – a) price and delta hedge for a given within Black-Scholes model – b) compute the associated final Profit & Loss: – c) solve for – d) repeat a) b) c) for general time period and average – e) repeat a) b) c) and d) to get the “theoretical Skew” Bruno Dupire 18
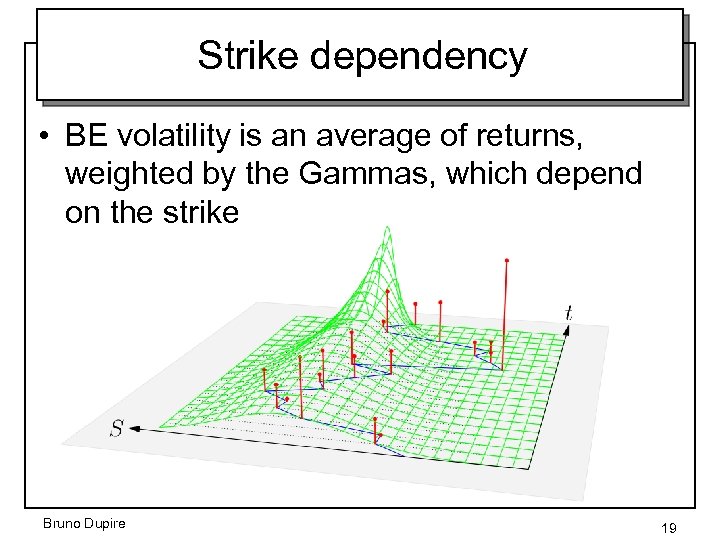
Strike dependency • BE volatility is an average of returns, weighted by the Gammas, which depend on the strike Bruno Dupire 19
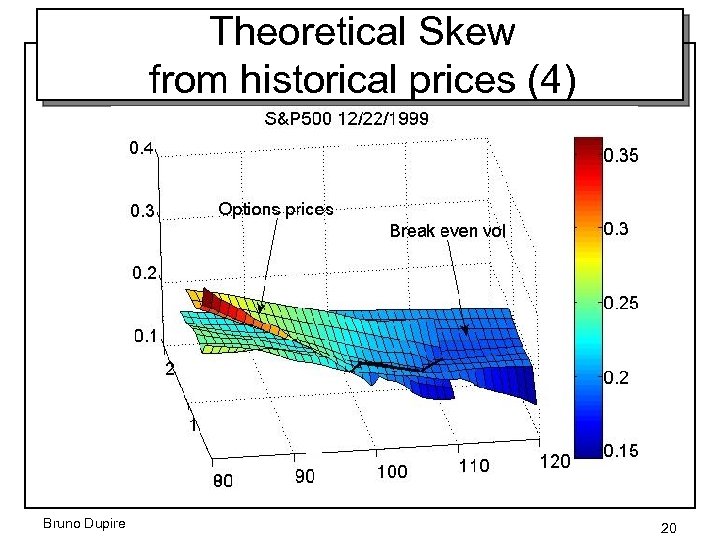
Theoretical Skew from historical prices (4) Bruno Dupire 20
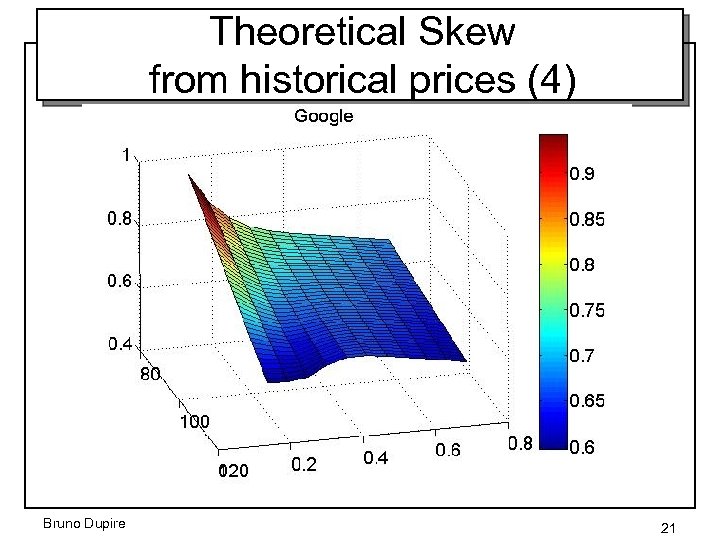
Theoretical Skew from historical prices (4) Bruno Dupire 21
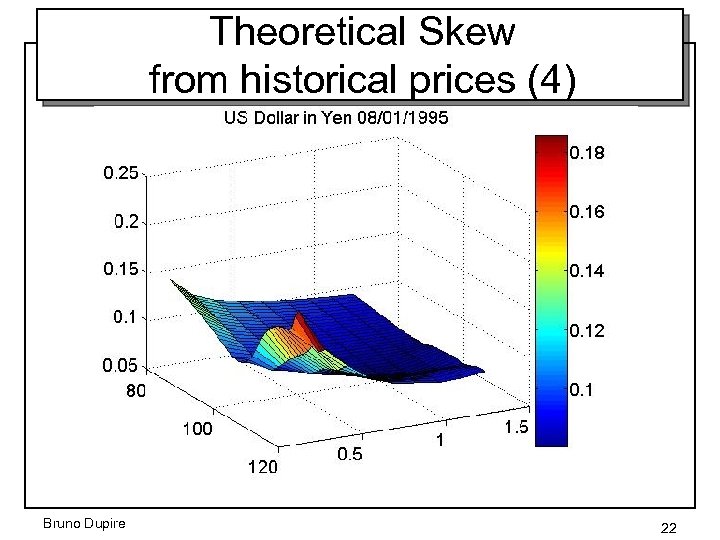
Theoretical Skew from historical prices (4) Bruno Dupire 22
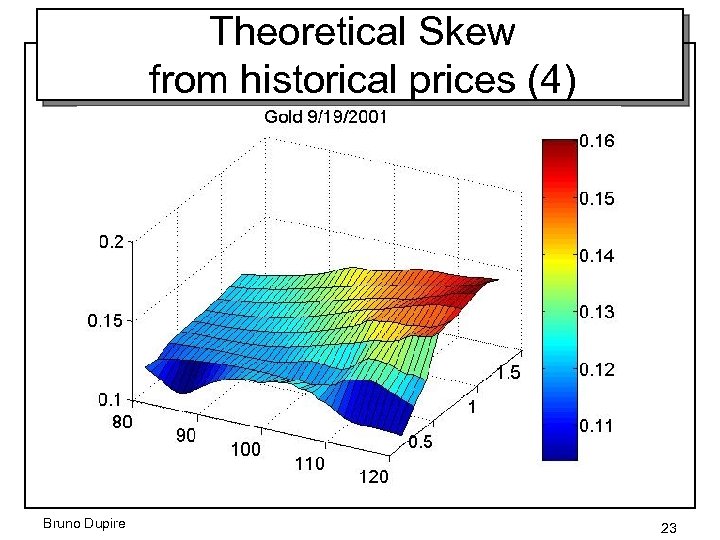
Theoretical Skew from historical prices (4) Bruno Dupire 23

Local Volatility Model Bruno Dupire

One Single Model • We know that a model with d. S = s(S, t)d. W would generate smiles. – Can we find s(S, t) which fits market smiles? – Are there several solutions? ANSWER: One and only one way to do it. Bruno Dupire 25
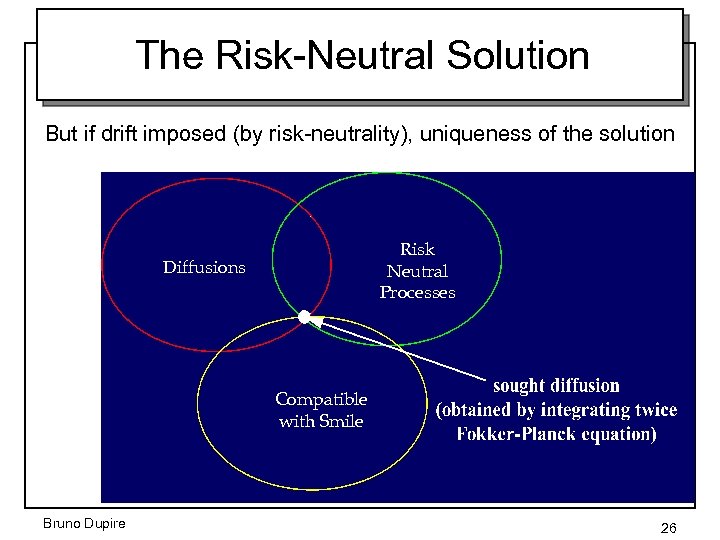
The Risk-Neutral Solution But if drift imposed (by risk-neutrality), uniqueness of the solution Risk Neutral Processes Diffusions Compatible with Smile Bruno Dupire 26

Forward Equation • BWD Equation: price of one option for different • FWD Equation: price of all options for current • Advantage of FWD equation: – If local volatilities known, fast computation of implied volatility surface, – If current implied volatility surface known, extraction of local volatilities: Bruno Dupire 27

Forward Equations (2) • Several ways to obtain them: – Fokker-Planck equation: • Integrate twice Kolmogorov Forward Equation – Tanaka formula: • Expectation of local time – Replication • Replication portfolio gives a much more financial insight Bruno Dupire 28

Volatility Expansion • K, T fixed. C 0 price with LVM • Real dynamics: • Ito • Taking expectation: • Equality for all (K, T) Bruno Dupire 29

Summary of LVM Properties is the initial volatility surface • compatible with local vol • compatible with (calibrated SVM are noisy versions of LVM) • deterministic function of (S, t) (if no jumps) future smile = FWD smile from local vol • Extracts the notion of FWD vol (Conditional Instantaneous Forward Variance) Bruno Dupire 30

Stochastic Volatility Models Bruno Dupire

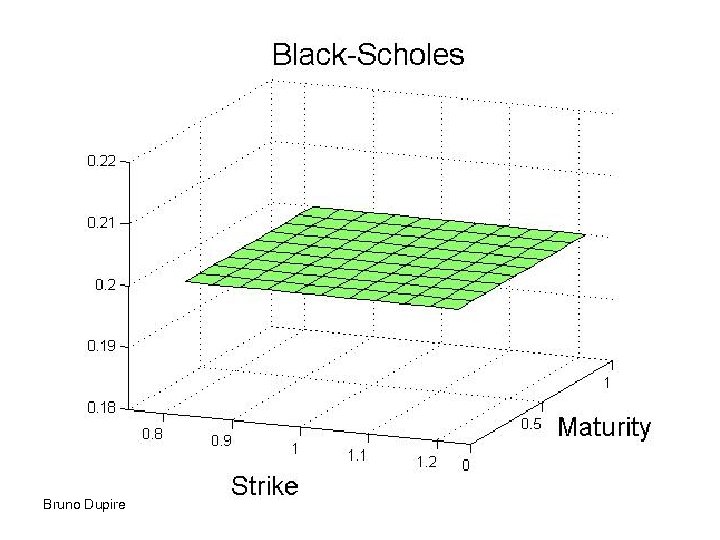
Heston Model Solved by Fourier transform: Bruno Dupire 32

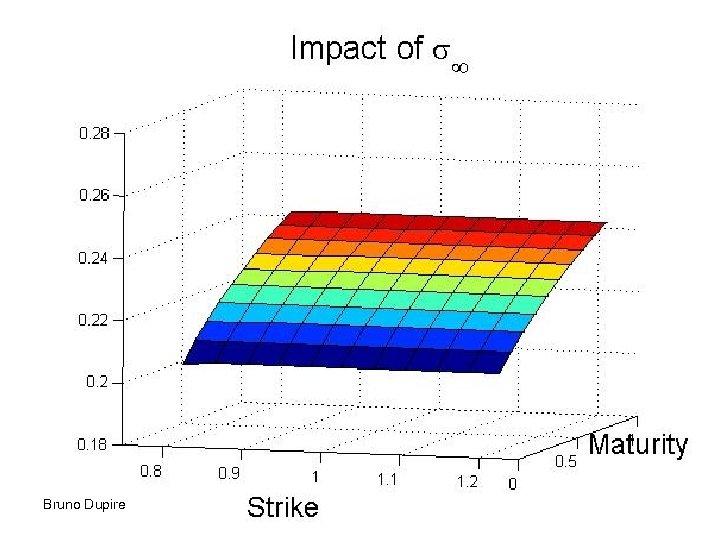
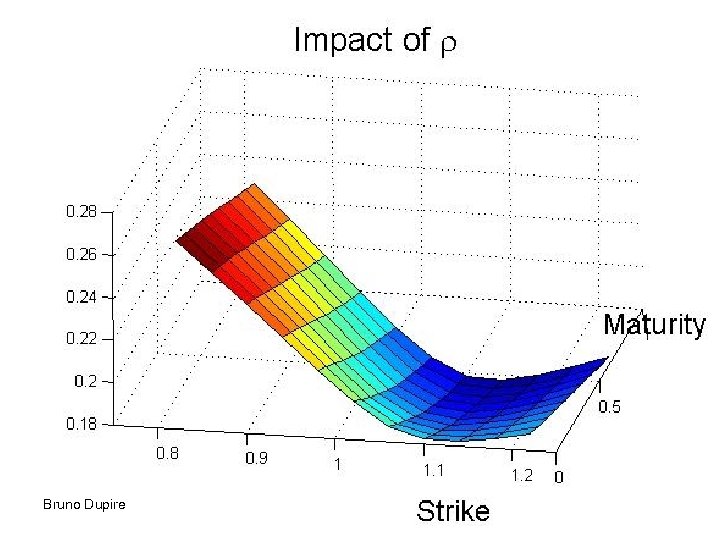
Role of parameters • Correlation gives the short term skew • Mean reversion level determines the long term value of volatility • Mean reversion strength – Determine the term structure of volatility – Dampens the skew for longer maturities • Volvol gives convexity to implied vol • Functional dependency on S has a similar effect to correlation Bruno Dupire 33
Bruno Dupire
Bruno Dupire

Bruno Dupire
Bruno Dupire
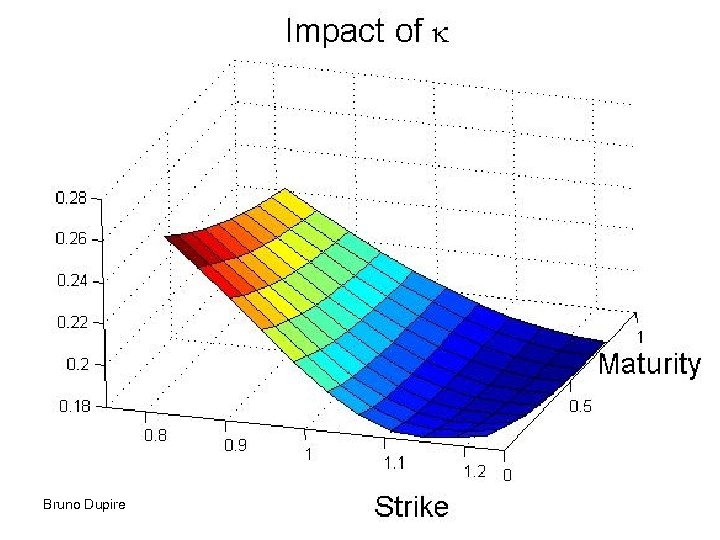
Bruno Dupire

Spot dependency 2 ways to generate skew in a stochastic vol model s s ST ST -Mostly equivalent: similar (St, st ) patterns, similar future evolutions -1) more flexible (and arbitrary!) than 2) -For short horizons: stoch vol model local vol model + independent noise on vol. Bruno Dupire 39
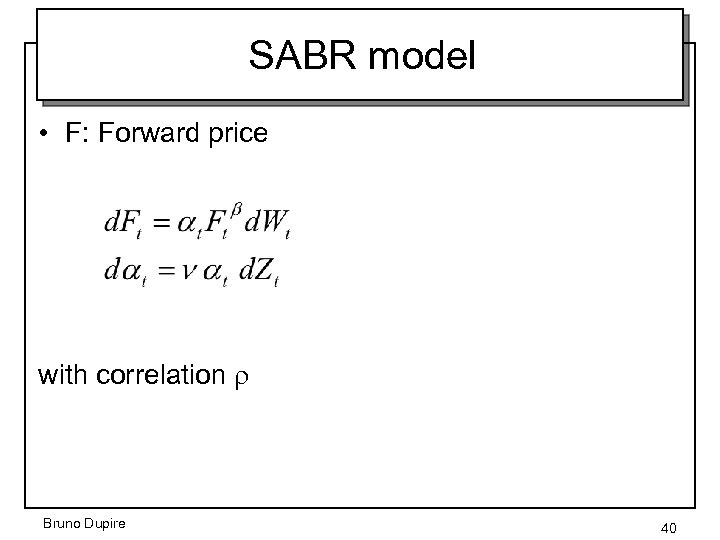
SABR model • F: Forward price with correlation r Bruno Dupire 40

Bruno Dupire
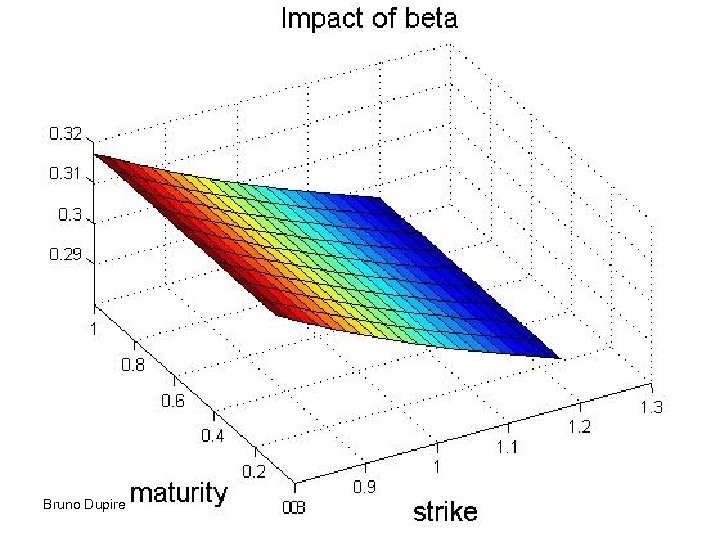
Bruno Dupire
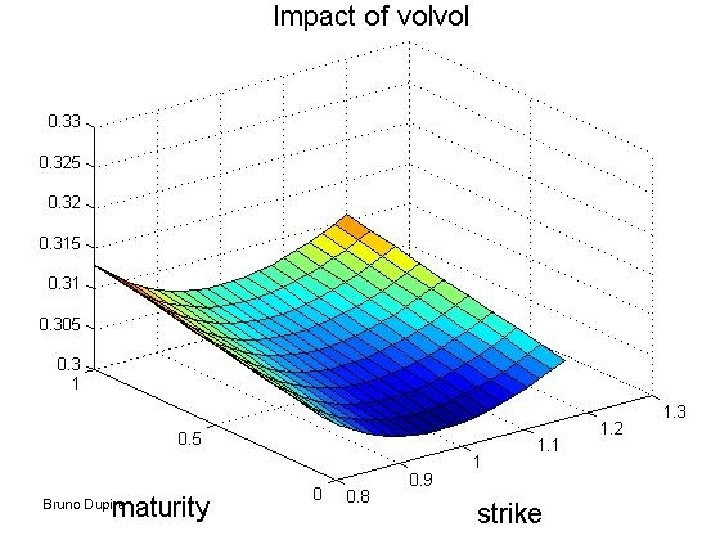
Bruno Dupire
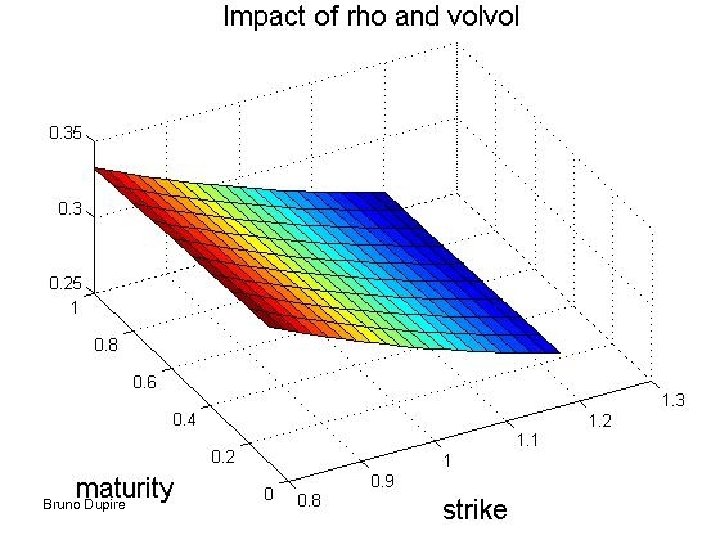
Bruno Dupire

Bruno Dupire
The SABR Claim Bruno Dupire 46
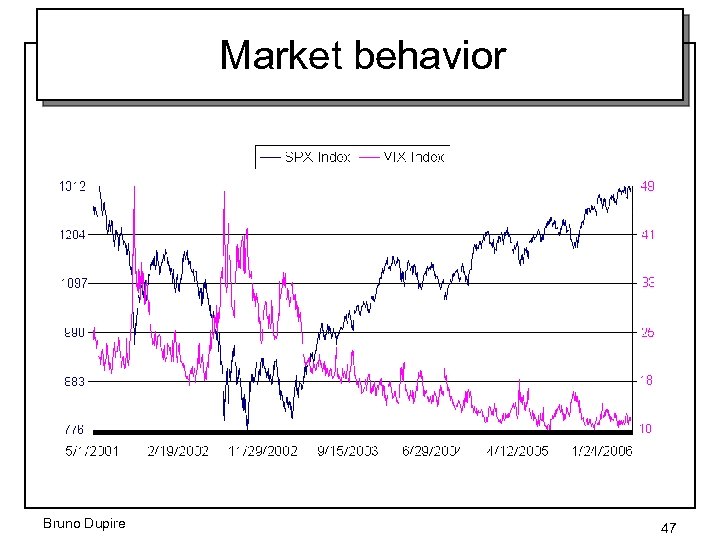
Market behavior Bruno Dupire 47

SABR fallacy • SABR claims to dissociate vol dynamics from Skew fitting • Many banks manage their vol risk with SABR • BUT if 2 SABR models fit the same skew, they generate essentially the same vol dynamics, which coincide in average with LVM dynamics! Bruno Dupire 48

Calibration according to SABR Backbone: as a function of F with frozen depends only on Many banks calibrate by: 1) Estimating from historical backbone 2) Then adjusting to fit the skew Bruno Dupire 49

Problems • Freezing ignores which actually impacts the average backbone • SABR can be rewritten with the lognormal volatility • In this parameterization instead of , freezing gives : the backbone is then constant! The backbone depends on the parameterization , it is not intrinsic to the model: it is a flawed concept Bruno Dupire 50

Message from LVM In particular for short maturities so average backbone ~ local vols! In the absence of jumps, the skew is due to average levels of vols higher on the downside If you were in that region increases Bruno Dupire 51
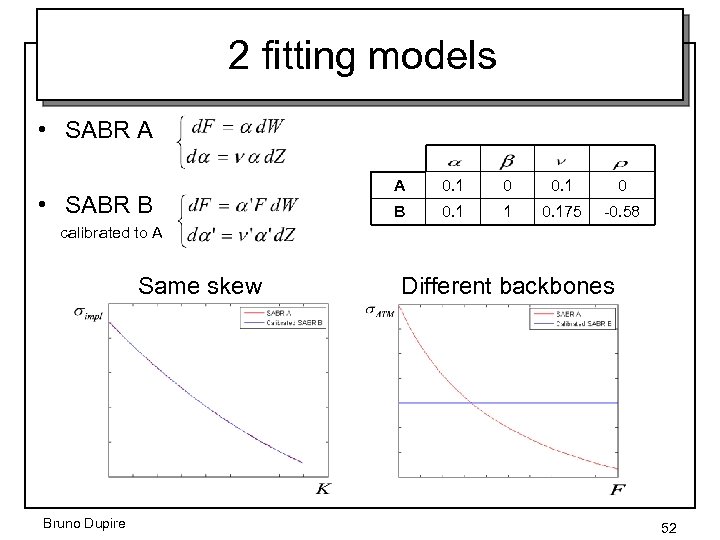
2 fitting models • SABR A • SABR B A 0. 1 0 B 0. 1 1 0. 175 -0. 58 calibrated to A Same skew Different backbones Bruno Dupire 52
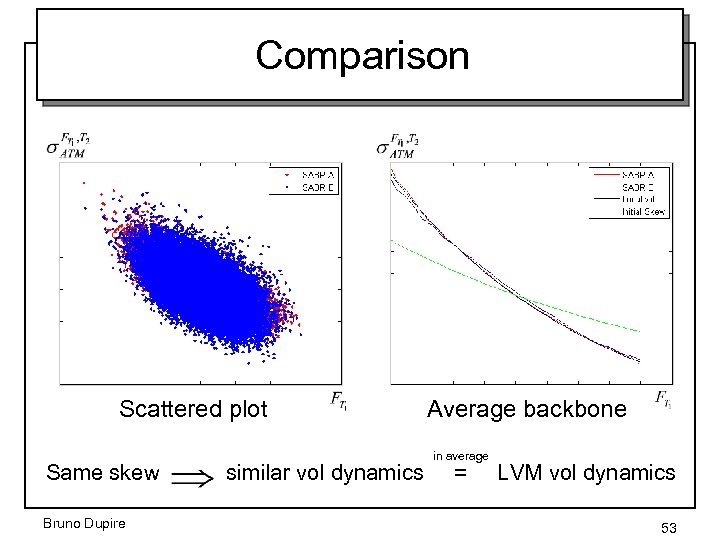
Comparison Scattered plot Average backbone in average Same skew similar vol dynamics = LVM vol dynamics Bruno Dupire 53

SABR Conclusion • To dissociate vol dynamics from skew fitting, jumps are needed • In a smile (as opposed to skew) dominated market, it is less clear as and cancel their first order impact • Banks may be unaware of the inconsistency of their risk management Bruno Dupire 54

Forward Skew Bruno Dupire

Forward Skews In the absence of jump : model fits market This constrains a) the sensitivity of the ATM short term volatility wrt S; b) the average level of the volatility conditioned to ST=K. a) tells that the sensitivity and the hedge ratio of vanillas depend on the calibration to the vanilla, not on local volatility/ stochastic volatility. To change them, jumps are needed. But b) does not say anything on the conditional forward skews. Bruno Dupire 56

Controlling Fwd Skew Many products depend on short term skew in the future Example: Napoleon, globally/locally capped/floored cliquet Local cap/floor: Global cap/floor: What does current vol surface tell us on future short term skew? Bruno Dupire 57
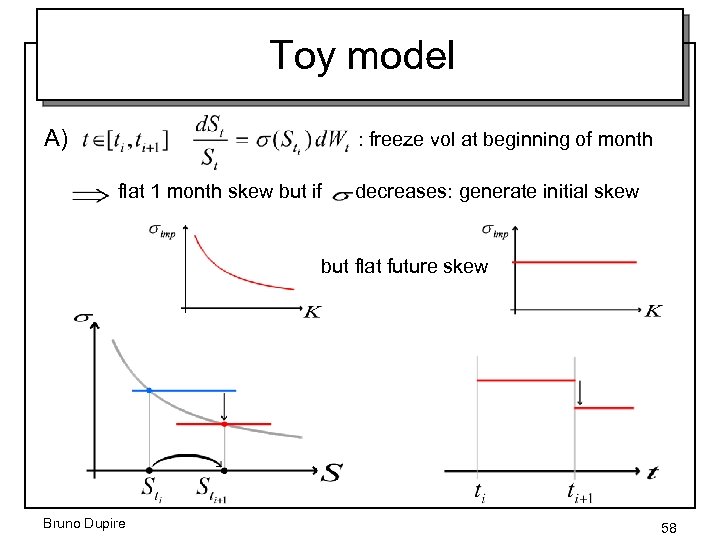
Toy model A) : freeze vol at beginning of month flat 1 month skew but if decreases: generate initial skew but flat future skew Bruno Dupire 58
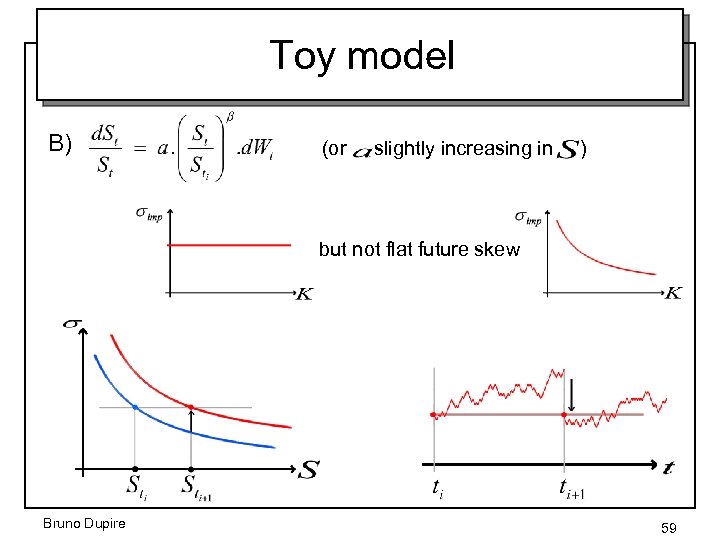
Toy model B) (or slightly increasing in ) but not flat future skew Bruno Dupire 59

Limitations • Behavior of future 1 month skew very different if start date is mid month instead of beginning of month • The amplitude of jumps is a measure of the wrongness of the model • LVM corresponds to the jumpless case Bruno Dupire 60

Sensitivity of ATM volatility / S At t, short term ATM implied volatility ~ σt. As σt is random, the sensitivity is defined only in average: In average, follows . Optimal hedge of vanilla under calibrated stochastic volatility corresponds to perfect hedge ratio under LVM. Bruno Dupire 61

Market Model of Implied Volatility • Implied volatilities are directly observable • Can we model directly their dynamics? where is the implied volatility of a given • Condition on dynamics? Bruno Dupire 62

Drift Condition • Apply Ito’s lemma to • Cancel the drift term • Rewrite derivatives of gives the condition that the drift of must satisfy. For short T, we get the Short Skew Condition (SSC): close to the money: Skew determines u 1 Bruno Dupire 63

Optimal hedge ratio ΔH • : BS Price at t of Call option with strike K, maturity T, implied vol • Ito: • Optimal hedge minimizes P&L variance: BS Delta Bruno Dupire BS Vega Implied Vol sensitivity 64

Optimal hedge ratio ΔH II With Skew determines u 1, which determines ΔH Bruno Dupire 65

Smile Arbitrage Bruno Dupire

Deterministic future smiles It is not possible to prescribe just any future smile If deterministic, one must have Not satisfied in general K S 0 t 0 Bruno Dupire T 1 T 2 67

Det. Fut. smiles & no jumps => = FWD smile If stripped from Smile S. t Then, there exists a 2 step arbitrage: Define At t 0 : Sell K S 0 t 0 S t T At t: gives a premium = PLt at t, no loss at T Conclusion: independent of from initial smile Bruno Dupire 68

Consequence of det. future smiles • Sticky Strike assumption: Each (K, T) has a fixed independent of (S, t) • Sticky Delta assumption: depends only on moneyness and residual maturity • In the absence of jumps, – Sticky Strike is arbitrageable – Sticky Δ is (even more) arbitrageable Bruno Dupire 69

Example of arbitrage with Sticky Strike Each CK, T lives in its Black-Scholes ( )world P&L of Delta hedge position over dt: If no jump ! Bruno Dupire 70

Arbitrage with Sticky Delta • In the absence of jumps, Sticky-K is arbitrageable and Sticky-Δ even more so. • However, it seems that quiet trending market (no jumps!) are Sticky-Δ. In trending markets, buy Calls, sell Puts and Δ-hedge. Example: S PF Vega > Vega S PF Δ-hedged PF gains from S induced volatility moves. Vega < Vega Bruno Dupire 71

Conclusion • Both leverage and asymmetric jumps may generate skew but they generate different dynamics • The Break Even Vols are a good guideline to identify risk premia • The market skew contains a wealth of information and in the absence of jumps, – – The spot correlated component of volatility The average behavior of the ATM implied when the spot moves The optimal hedge ratio of short dated vanilla The price of options on RV • If market vol dynamics differ from what current skew implies, statistical arbitrage Bruno Dupire 72

BLOOMBERG, BLOOMBERG PROFESSIONAL, BLOOMBERG MARKETS, BLOOMBERG NEWS, BLOOMBERG ANYWHERE, BLOOMBERG TRADEBOOK, BLOOMBERG BONDTRADER, BLOOMBERG TELEVISION, BLOOMBERG RADIO, BLOOMBERG PRESS and BLOOMBERG. COM are trademarks and service marks of Bloomberg Finance L. P. , a Delaware limited partnership, or its subsidiaries. The BLOOMBERG PROFESSIONAL service (the "BPS") is owned and distributed locally by Bloomberg Finance L. P. (BFLP) and its subsidiaries in all jurisdictions other than Argentina, Bermuda, China, India, Japan and Korea (the "BLP Countries"). BFLP is a wholly -owned subsidiary of Bloomberg L. P. ("BLP"). BLP provides BFLP with all global marketing and operational support and service for these products and distributes the BPS either directly or through a non-BFLP subsidiary in the BLP Countries. Bruno Dupire 73
c6fe9c1b11f0081c526594e7f5c70b40.ppt