Modelling Transport Phenomena during Spreading and Solidification of

Modelling Transport Phenomena during Spreading and Solidification of Droplets in Plasma Projection Dominique GOBIN CNRS – France NGU Seminar Nova Gorica (November 5, 2009)

Contents 1. Motivation 2. Equations 3. Isothermal spreading 4. Spreading with solidification 5. Perspective 2

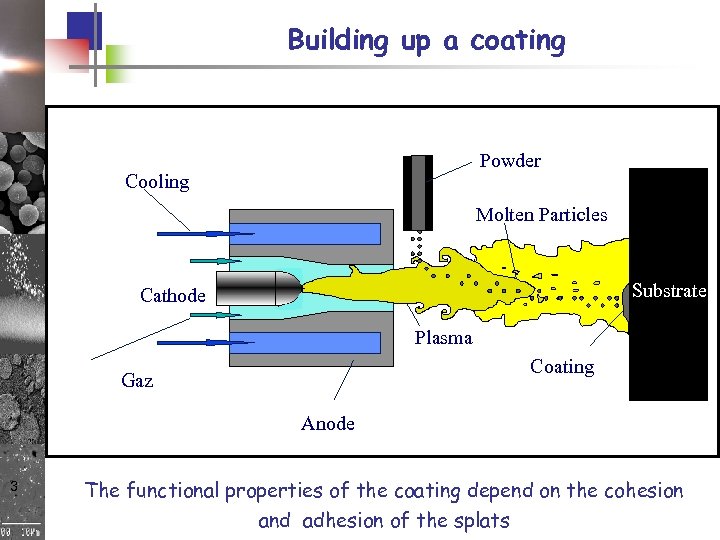Building up a coating Powder Cooling Molten Particles Substrate Cathode Plasma Coating Gaz Anode 3 The functional properties of the coating depend on the cohesion and adhesion of the splats

4

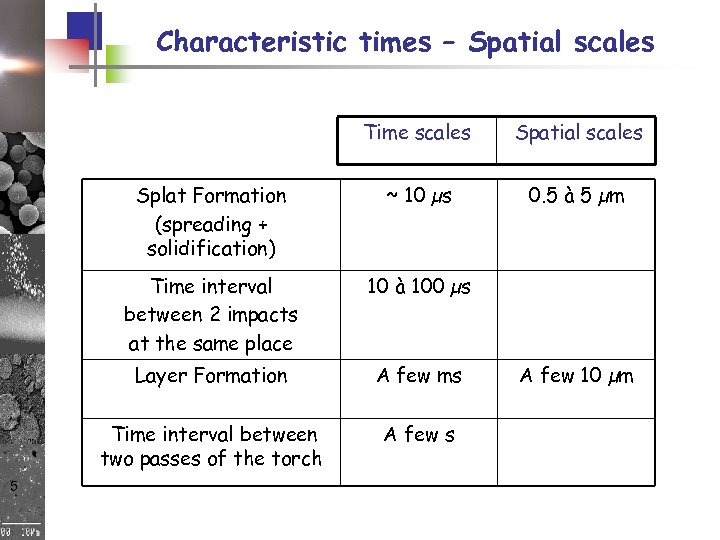Characteristic times – Spatial scales Time scales Splat Formation (spreading + solidification) ~ 10 µs 0. 5 à 5 µm Time interval between 2 impacts at the same place 10 à 100 µs Layer Formation A few ms Time interval between two passes of the torch 5 Spatial scales A few 10 µm

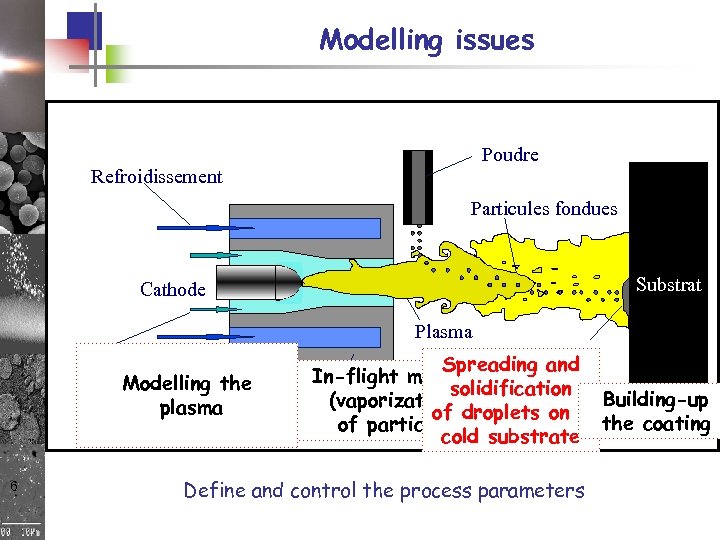Modelling issues Poudre Refroidissement Particules fondues Substrat Cathode Plasma Gaz Modelling the plasma 6 Spreading. Dépôt and In-flight melting solidification Building-up (vaporization) of droplets on a Anode particles the coating of cold substrate Define and control the process parameters

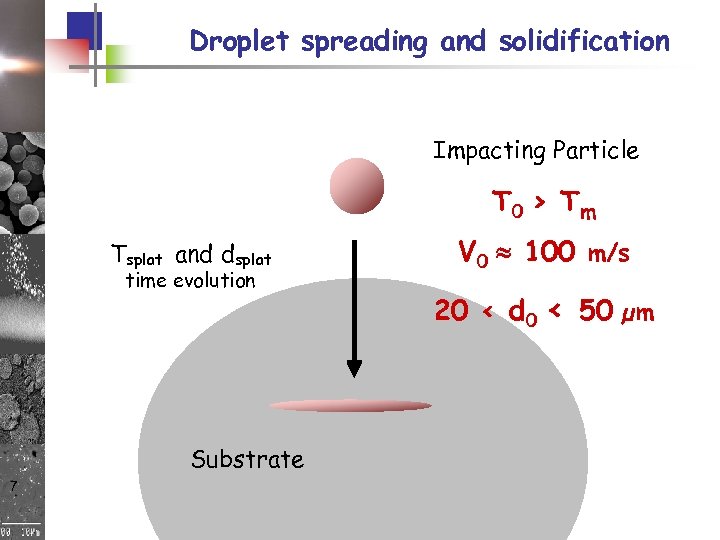Droplet spreading and solidification Impacting Particle T 0 > Tm Tsplat and dsplat time evolution V 0 100 m/s 20 < d 0 < 50 µm Ts Substrate 7

2. Equations 8

Modelling spreading Pure fluid dynamics problem. The substrate is a boundary condition Mass Conservation Momentum Conservation 9

Modelling spreading Non-dimensionalizing variables (choosing reference values d 0, V 0, etc…) yields the dimensionless parameters of the problem Mass Conservation Momentum Conservation 10

Modelling spreading with solidification Coupling the equations of fluid dynamics with the heat transfer equations Mass Conservation Momentum Conservation Energy Conservation - in the splat 11 - in the substrate

Modelling spreading with solidification During solidification two phases (solide and fluid) are present. 1 if liquid A phase function is defined : = Mass Conservation 0 if solid Momentum Conservation 12

Modelling spreading with solidification Energy Conservation Heat transfer and enthalpy formulation 13

Conservation equations Mass Conservation Momentum Conservation Energy Conservation Liquid Fraction 14 = 1 liquid 0 solid

Physical parameters of the problem Parameters of the particles at impact Nature Size Velocity Temperature and state of melting Parameters of the substrate Nature Rugosity Initial temperature Surface chemistry (wettability) 15

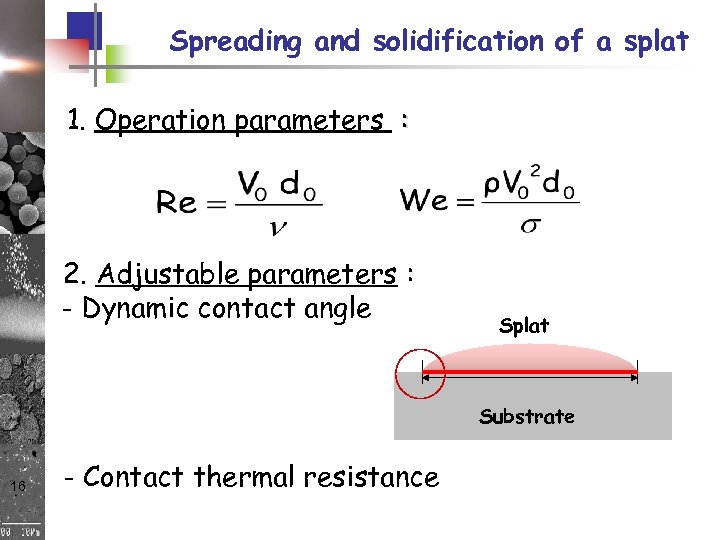Spreading and solidification of a splat 1. Operation parameters : 2. Adjustable parameters : - Dynamic contact angle Splat Substrate 16 - Contact thermal resistance

Numerical tool Simulent-Drop : a software developed at the University of Toronto (J. Mostaghimi et al. ) Main hypotheses § Newtonian fluid § Constant properties (surface tension, contact resistance, conductivities, viscosity, …) § Equilibrium solidification 17

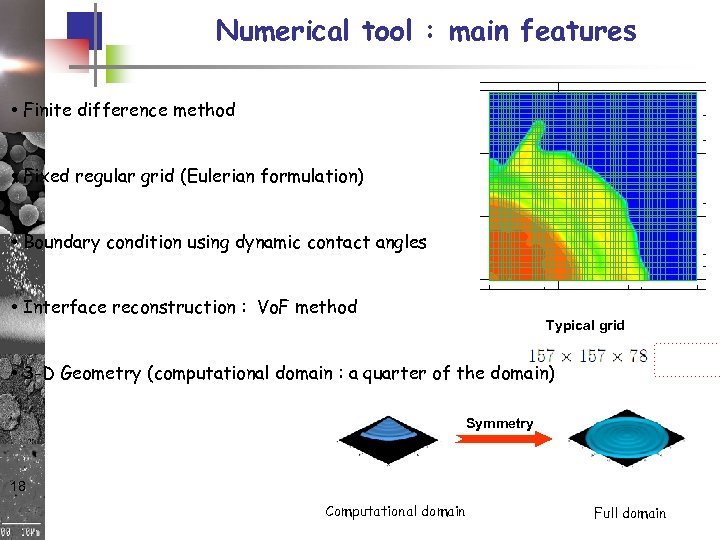Numerical tool : main features • Finite difference method • Fixed regular grid (Eulerian formulation) • Boundary condition using dynamic contact angles • Interface reconstruction : Vo. F method Typical grid • 3 -D Geometry (computational domain : a quarter of the domain) Symmetry 18 Computational domain Full domain

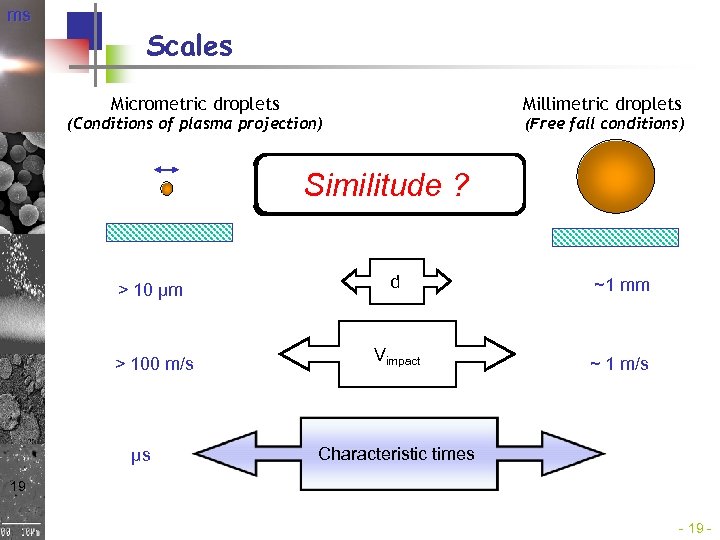ms Scales Micrometric droplets Millimetric droplets (Conditions of plasma projection) (Free fall conditions) Re ~ identiques Similitude ? We ~10 à 100 fois plus grand > 10 µm d ~1 mm > 100 m/s Vimpact ~ 1 m/s µs Characteristic times 19 -

3. Isothermal spreading 20

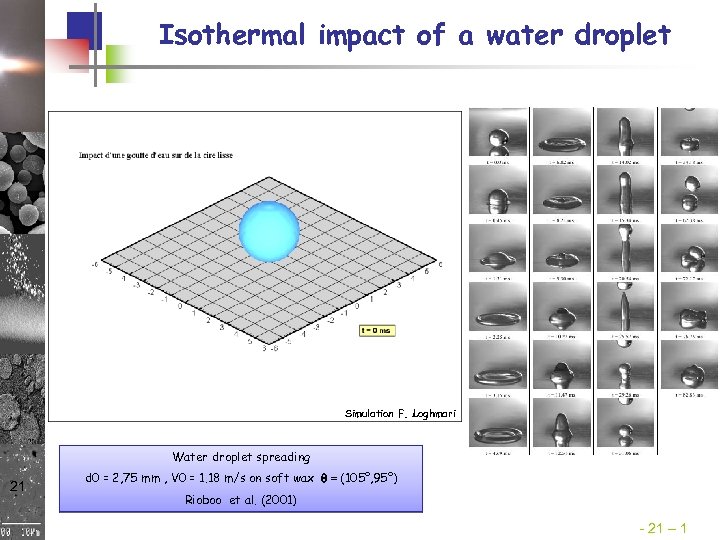Isothermal impact of a water droplet Simulation F. Loghmari Water droplet spreading 21 d 0 = 2, 75 mm , V 0 = 1. 18 m/s on soft wax q = (105°, 95°) Rioboo et al. (2001) - 21 – 1

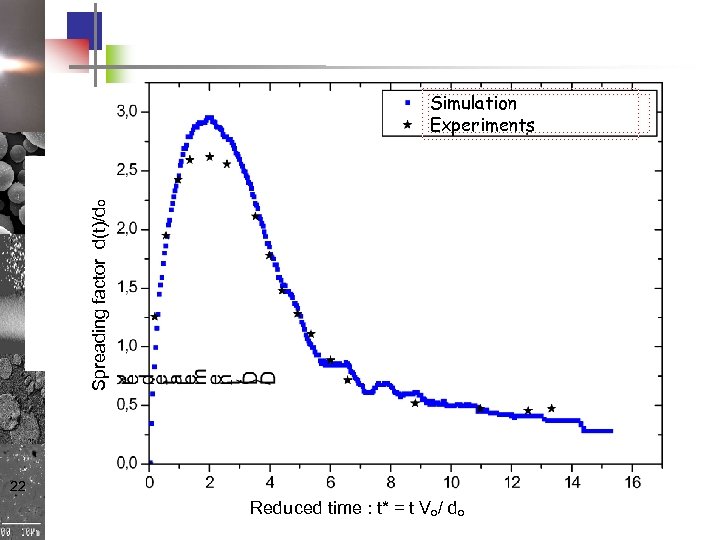Spreading factor d(t)/do Simulation Experiments 22 Reduced time : t* = t Vo/ do

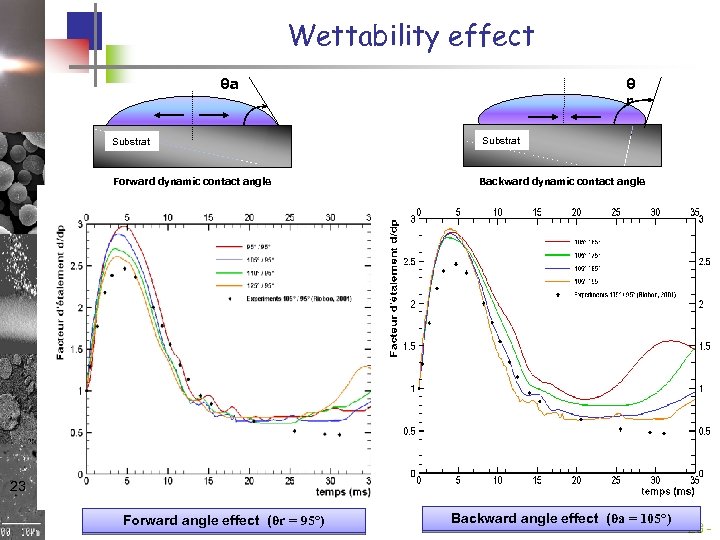Wettability effect θa θ r Substrat Forward dynamic contact angle Backward dynamic contact angle 23 Forward angle effect (θr = 95°) Backward angle effect (θa = 105°) - 23 -

4. Spreading with solidification 24

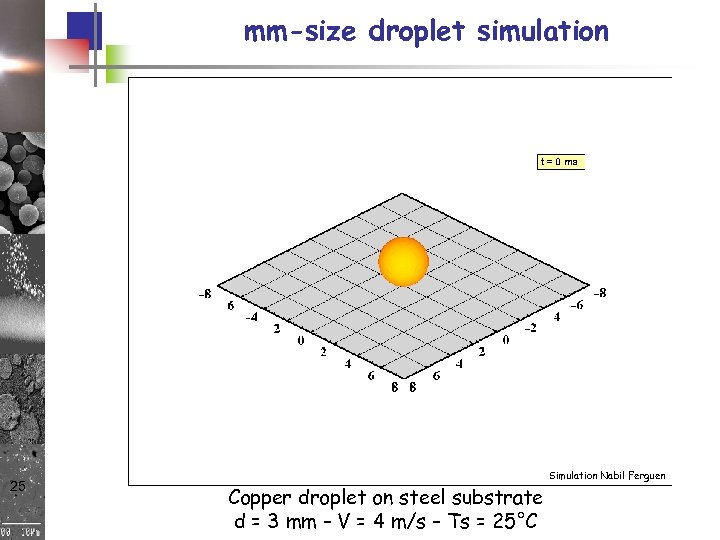mm-size droplet simulation 25 Copper droplet on steel substrate d = 3 mm – V = 4 m/s – Ts = 25°C Simulation Nabil Ferguen

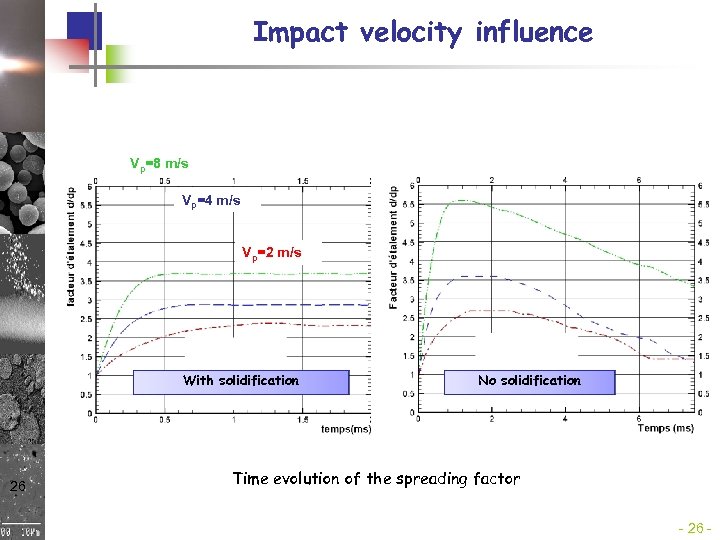Impact velocity influence Vp=8 m/s Vp=4 m/s Vp=2 m/s With solidification 26 No solidification Time evolution of the spreading factor - 26 -

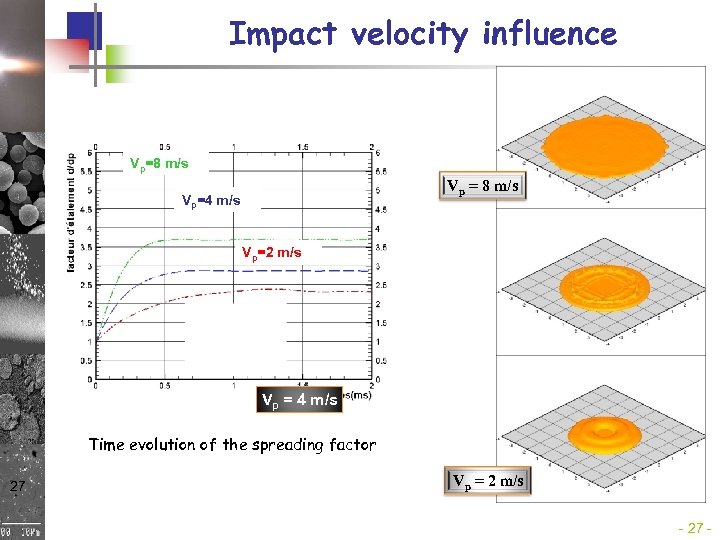Impact velocity influence Vp=8 m/s Vp = 8 m/s Vp=4 m/s Vp=2 m/s Vp = 4 m/s Time evolution of the spreading factor 27 Vp = 2 m/s - 27 -

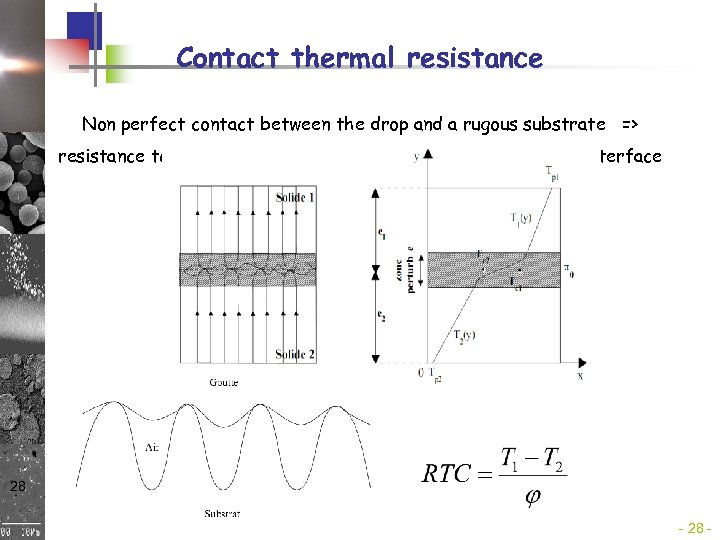Contact thermal resistance Non perfect contact between the drop and a rugous substrate => resistance to the heat flux : temperature discontinuity at the interface CTR Model 28 -

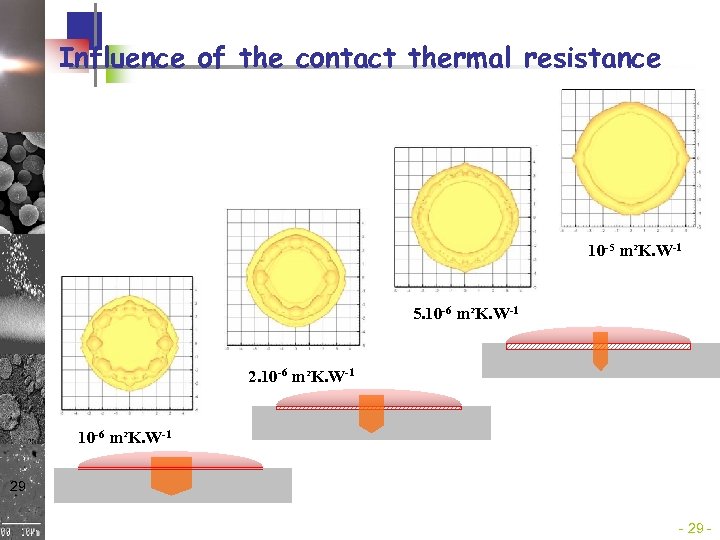Influence of the contact thermal resistance 10 -5 m²K. W-1 5. 10 -6 m²K. W-1 29 -

High contact resistance RTC = 10 -5 m²K. W-1 30 Copper droplet on steel substrate d = 3 mm – V = 4 m/s – Ts = 400°C Simulation Nabil Ferguen

Low contact resistance RTC = 10 -6 m²K. W-1 31 Copper droplet on steel substrate d = 3 mm – V = 4 m/s – Ts = 400°C Simulation Nabil Ferguen

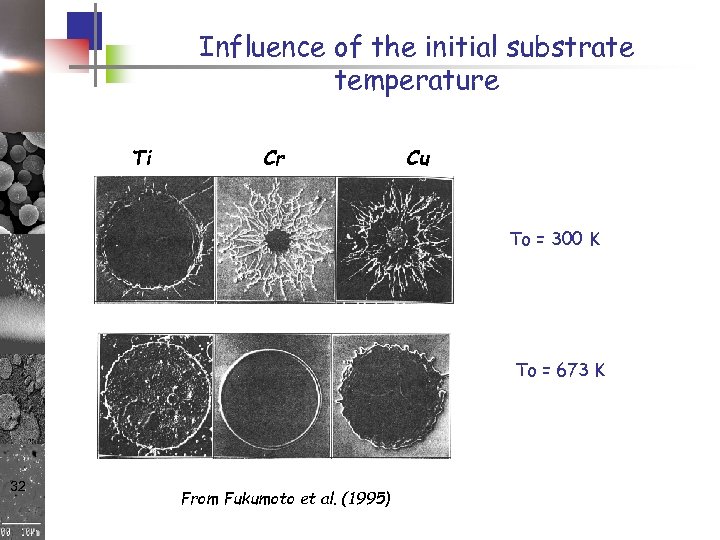Influence of the initial substrate temperature Ti Cr Cu To = 300 K To = 673 K 32 From Fukumoto et al. (1995)

Splat formation Morphological transition temperature Tt Alumina on steel 304 L 33 « Splash » Cold substrate Tsub< Tt Poor adhesion of the coating ( 4 MPa) « Splat » Pre-heated substrate Tsub> Tt Better adhesion ( 30 MPa)

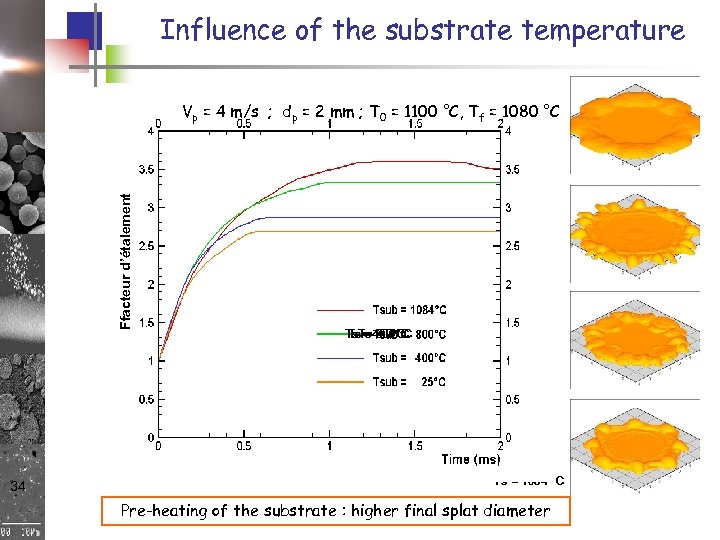Influence of the substrate temperature Vp = 4 m/s ; dp = 2 mm ; T 0 = 1100 °C, Tf = 1080 °C Ffacteur d’étalement Re = 23900 , We = 191 34 Ts = 800°C Ts = 25°C Ts = 400°C Ts = 1084 °C Pre-heating of the substrate : higher final splat diameter

Transition Temperature ? § Desorption of adsorbates and condensates § Modification of wettability of the substrate § Modification thermal resistance Possible evolution of the surface state of the substrate 35

5. Further developments 36

Non equilibrium Solidification • Basic hypothesis : solidification at equilibrium Most models do not take into account undercooling, nucleation and growth : problem of multi-scale (micro + macro) simulation But in plasma projection, the cooling velocity measured in the experiments reaches from 106 to 5. 108 K/s : undercooling about 0, 1 to 0, 2 Tm. Include rapid solidification 37

Film S. Goutier – M. Vardelle Experiments on mm-size droplets 38 Alumina droplet on steel substrate d = 5 mm – V = 10 m/s – Ts = 400°C

Thank you for your attention Special Thanks to : • Nabil Ferguen : SPCTS Laboratory • Simon Goutier : SPCTS Laboratory • Fahmi Loghmari : FAST Laboratory 39

40

Isothermal impact of a water droplet Simulation F. Loghmari Water droplet spreading 41 d 0 = 2, 75 mm , V 0 = 1. 18 m/s on soft wax q = (105°, 95°) Rioboo et al. (2001) - 41 – 1