MODELLEMEYE GİRİŞ — 1 Doç Dr Ali Ertürk

MODELLEMEYE GİRİŞ - 1 Doç. Dr. Ali Ertürk 02/03/2015

Model Nedir? • Alıcı ortamın maruz kaldığı etkilere karşı; fiziksel, kimyasal ve biyolojik yapısı itibari ile vereceği tepkilerin tespit edilmesini sağlayan, günümüzde özellikle bilgisayar kullanımı ile geliştirilen araçlardır. • Gerçek ekosistemlerin basitleştirilmesi ve idealleştirilmesi ile problemlerin çözülmesine yararlar.

Modellerin Faydaları • Modeller kullanılarak izleme verileri ile zamanda ve konumda interpolasyon yapabilirler. • İzleme ağının çözünürlüğü ne kadar yüksek olursa olsun, bir sisteminin her anının ve noktasının izleme kapsamına alınması mümkün değildir. • Doğrulanmış modeller ise ölçüm olmayan zaman ve konumlardaki su kalitesinin tahmin edilmesinde kullanılabilinmektedirler. • Modeller yardımıyla alıcı ortamlar üzerinde değişik hipotezler sanal olarak denenebilmektedir. Gerçekleşmemiş olayların sonuçlarının da öngörülmeleri mümkündür. (Senaryo analizleri).

Örnek Senaryolar • Yönetilen su ekosisteminin önemli çevresel sorunları yok ama özümleme kapasitesi belirlenmeye çalışılıyor. Bu ekosistem “özümleme kapasitesi aşılana kadar kirletilip çevresel sorunların gözlediği kirletici yükünün özümleme kapasitesi olarak tanımlanması” bir belirleme yöntemi olamayacağına göre model tabanlı bir simülasyon yapılması gerekmektedir. • İklim değişikliği, üzerinde çalışılan ekosistemindeki su kalitesini nasıl etkileyecek? • Su kaynağının havzasında tarım %50 artarsa ne olur? • Su kaynağına aniden bir kirletici dökülüyor. Bu kirleticinin su alma ağzında zararlı konsantrasyonlara ulaşması ne kadar sürer?

Modellerin Faydaları • Çevre sorunlarının çözülmesi için en uygun seçeneğin belirlenmesi çalışmalarında zaman ve para tasarrufu sağlarlar. • Değişik senaryolar ve çevre risklerinin daha iyi analiz edilmesini sağlarlar. • Doğal proseslerin ve sistemin nasıl işlediğinin daha iyi anlaşılmasını sağlarlar. • Modeller gelecekteki durum ile ilgili yorum yapılabilmesini sağlarlar.

Modellerin Kullanım Amaçları • Çevre problemlerinin ve risklerinin belirlenmesine ve kirliliğin önlenmesinde yardımcı araç olarak • Gelecek senaryolarının kurulup, sürdürülebilir kalkınma da göz önünde bulundurularak, çeşitli yönetim planlarının yapılmasında • Bu planlar doğrultusunda alınacak önlemlerin çevresel etkilerinin ve maliyetlerinin önceden tahmin edilmesinde • İzleme ağlarının tasarımında • Kirlenmeye karşı önlemlerin ve islah çalışmalarının muhtemel sonuçlarının belirlenmesinde • Risk altındaki alıcı ortamların belirlenmesinde • Eksik verilerin tamamlanmasında • Su kalitesini etkileyen önemli proseslerin belirlenmesinde • Mevcut su kalitesinin detaylı olarak analizinde

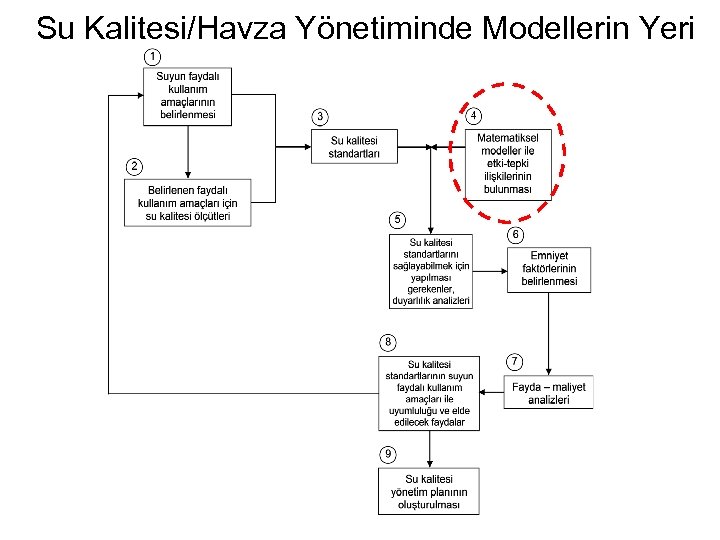Su Kalitesi/Havza Yönetiminde Modellerin Yeri

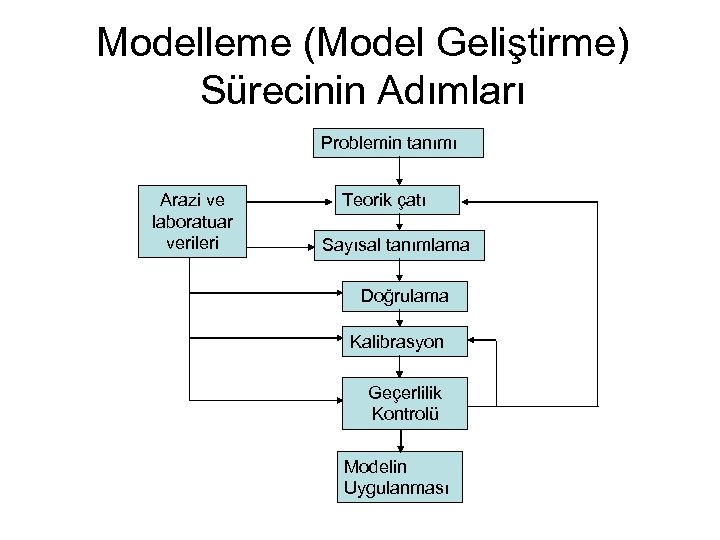Modelleme (Model Geliştirme) Sürecinin Adımları Problemin tanımı Arazi ve laboratuar verileri Teorik çatı Sayısal tanımlama Doğrulama Kalibrasyon Geçerlilik Kontrolü Modelin Uygulanması

Doğrulama Geliştirilen modelin hesap sisteminin ya da modelleme yazılımlarının doğru çalıştıklarından emin olunmalıdır. Aşağıdaki testler mutlaka yapılmalıdır. • Model, sistemin kütle dengesini koruyabiliyor mu? • Su kalitesi değişkenleri arasındaki ilişkiler beklendiği gibi mi? • Kullanılan sayısal çözüm yöntemleri, model ortamında canlandırılan ekosistemin yapısını temsil etmeye uygun mu?

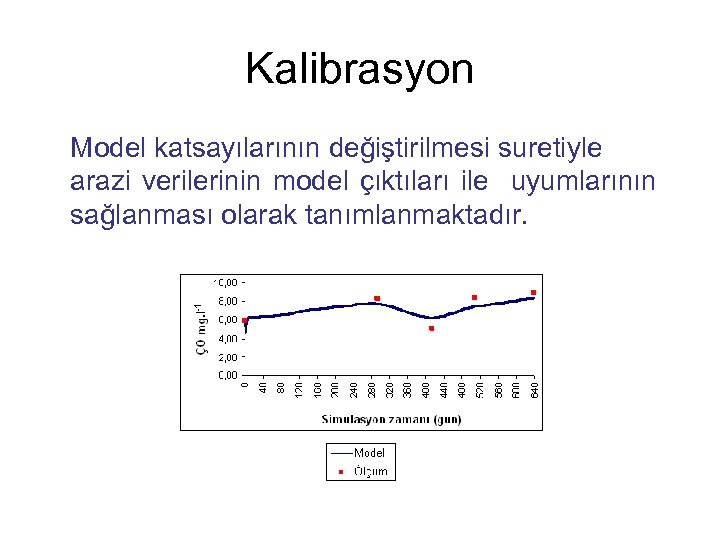Kalibrasyon Model katsayılarının değiştirilmesi suretiyle arazi verilerinin model çıktıları ile uyumlarının sağlanması olarak tanımlanmaktadır.

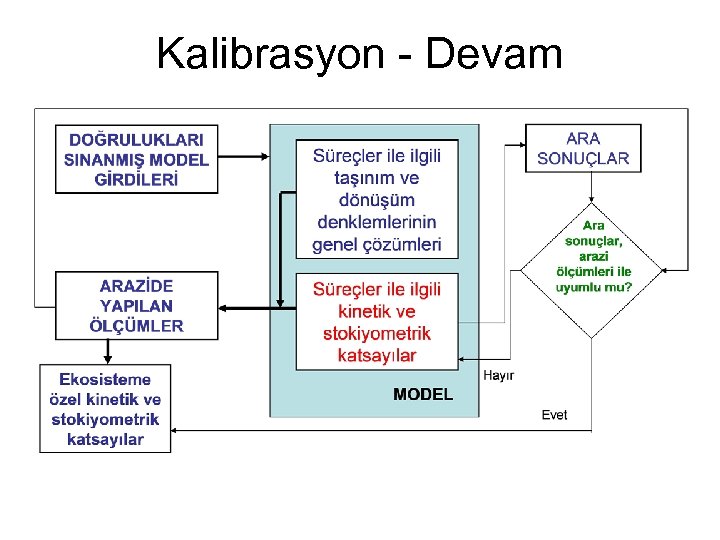Kalibrasyon - Devam

Kalibrasyon - Devam • Karmaşık modellerin kalibrasyonları da uzun sürebilmektedir. • Model katsayıları ekosistem için kalibre edilene kadar modelin binlerce kez çalıştırılması gerekebilmektedir. • Bu zor, sıkıcı ve pek de üretken olmayan bir süreçtir. • Bu nedenle otomatik kalibrasyon algoritmaları geliştirilmiştir.

Geçerlilik Kontrolü Kalibre edilmiş modelin mümkün olduğu kadar farklı koşullar için yeniden çalıştırılıp üretilen sonuçların farklı koşulları temsil eden arazi verileriyle karşılaştırılması olarak tanımlanmaktadır.

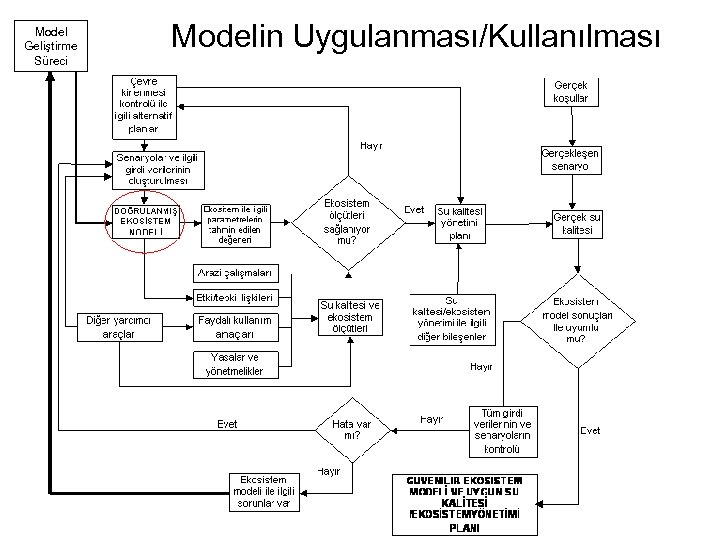Model Geliştirme Süreci Modelin Uygulanması/Kullanılması

Matematiksel Model Sınıfları Ampirik Modeller Örneğin fosfor ve chl-A arasındaki ilişkiyi deneysel verilerin analiziyle elde eden modellerdir. Kuramsal Modeller Bu tip modeller etkin mekanizmaları matematiksel denklemlerle ifade edip olayları açıklayacak şekilde tasarlanmaktadır.

Kuramsal Modellerin Prensipleri Kütle Korunumu Kanunu Doğada enerji ve madde vardan yok olamaz. Yoktan var olamaz. Ancak dönüşümlere uğrayabilir. Teori ağırlıklı modellerdeki hesaplar bu kanuna dayanmaktadır. Korunan Özelliklere Örnekler: • Kütle (su kütlesi, bileşen kütlesi) (Su kütlesi = yoğunluk x hacim) (Bileşen kütlesi = konsantrasyon x hacim) • Momentum (Momentum = kütle x hız) • Isı

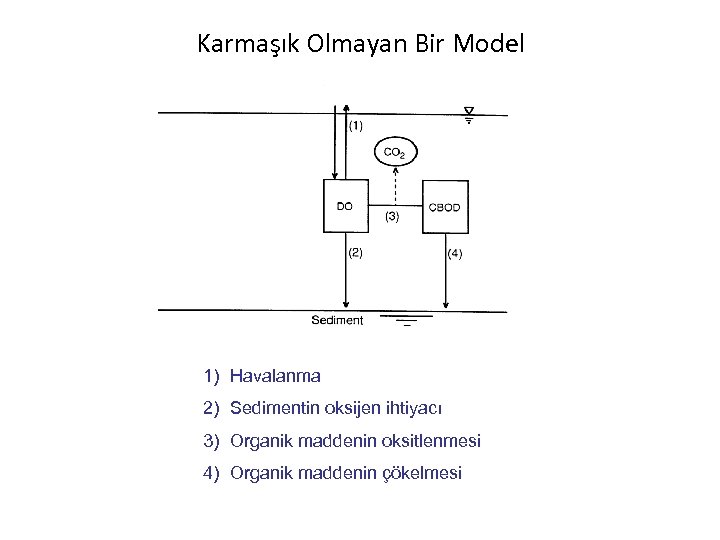Karmaşık Olmayan Bir Model 1) Havalanma 2) Sedimentin oksijen ihtiyacı 3) Organik maddenin oksitlenmesi 4) Organik maddenin çökelmesi

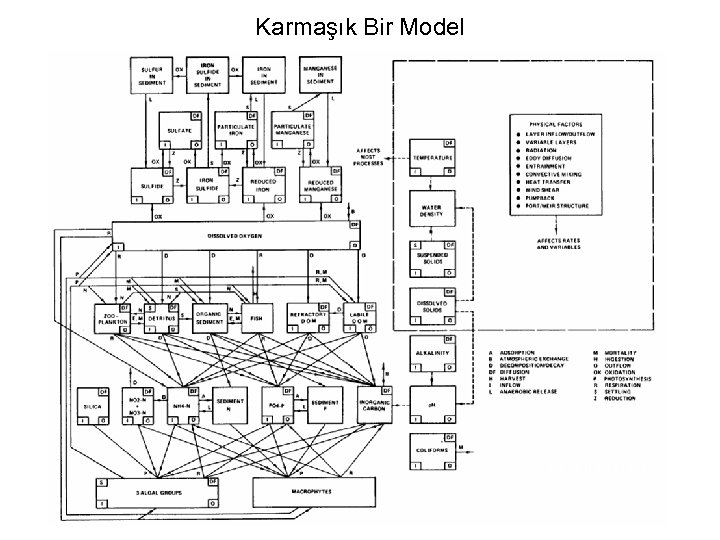Karmaşık Bir Model CE-QUAL-R 1

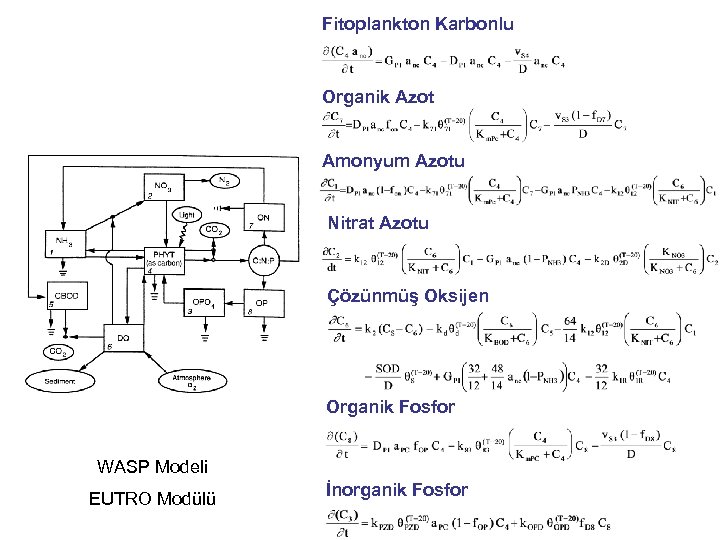Fitoplankton Karbonlu Organik Azot Amonyum Azotu Nitrat Azotu Çözünmüş Oksijen Organik Fosfor WASP Modeli EUTRO Modülü İnorganik Fosfor

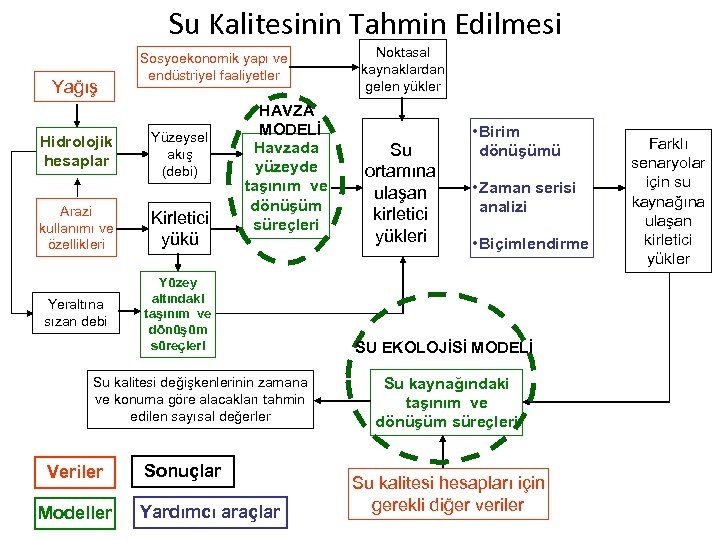Su Kalitesinin Tahmin Edilmesi Yağış Hidrolojik hesaplar Sosyoekonomik yapı ve endüstriyel faaliyetler Yüzeysel akış (debi) Arazi kullanımı ve özellikleri Kirletici yükü Yeraltına sızan debi HAVZA MODELİ Havzada yüzeyde taşınım ve dönüşüm süreçleri Yüzey altındaki taşınım ve dönüşüm süreçleri Su kalitesi değişkenlerinin zamana ve konuma göre alacakları tahmin edilen sayısal değerler Veriler Modeller Sonuçlar Yardımcı araçlar Noktasal kaynaklardan gelen yükler Su ortamına ulaşan kirletici yükleri • Birim dönüşümü • Zaman serisi analizi • Biçimlendirme SU EKOLOJİSİ MODELİ Su kaynağındaki taşınım ve dönüşüm süreçleri Su kalitesi hesapları için gerekli diğer veriler Farklı senaryolar için su kaynağına ulaşan kirletici yükler

Havza/Hidrolojik Modeller • SWAT • HSPF • Ve daha onlarcası

Hidrodinamik Modeller • • • SHYFEM* TELEMAC MOHID* EFDC* SSIIM* CE-QUAL-W 2* * Su kalitesi/ekolojisi bileşenleri de var.

Su Kalitesi/Ekolojisi Modelleri • • AQUATOX WASP ECOPATH ve ECOSIM CE-QUAL-R 1 WQRRS ESTAS SİSMOD EGÖLEM

Modelleme İçin Gerekli Bileşenler • Donanım • Yazılım • Modelleme konusunda yetişmiş uzman personel • Ve en önemlisi veri

GEREKLİ VERİLER

MODELLEMENİN UYMAMA SEÇENEĞİ OLMAYAN ÜÇ KURALI • Modeller; su, enerji ve kütlenin korunumu üzerine kuruludur. • Modellenen ortam bilgisayar ortamında gerçeğe mümkün olan en yakın şekilde temsil edilmelidir. Bu koşul ancak kurumlarımızın ellerindeki verileri paylaşmaları ile gerçekleştirilebilir. • Toplam üç kural vardır.

Havza Modellerinin Çalıştırılması İçin Gerekli Veriler • Topgrafya (SYM) • Akarsular ve göletlerle ilgili geometrik veriler (Batimetri, enkesit, vb) • Su mühendisliği yapılarının özellikleri (Göletler, küçük barajlar, köprüler, bağlamalar, su alma yapıları, sulama yapıları, vb. ) • Su kullanımı ile ilgili ayrıntılı* veriler (aylık) • Su ortamlarına deşarjlar ile ilgili ayrıntılı** veriler (aylık) * Ne zaman, hangi kaynaktan ne kadar su alınıyor. ** Ne zaman, nereye, hangi debi ve kalitede (modellenmesi istenen parametreler açısından) deşarj var.

Havza Modellerinin Çalıştırılması İçin Gerekli Veriler - Devam • Arazi kullanımı ve özellikleri - tarım, orman alanları ve yerleşim alanları - sayısallaştırılmış köy sınırlar (mümkün değilse ilçe sınırları) - mümkün olduğu kadar çok yıl için köy ölçeğinde gübre kullanımı ve hayvanclılık verileri (mümkün değilse ilçe) - ürün deseni ve zirai operasyonlar - jeoloji ve hidrojeoloji

Havza Modellerinin Çalıştırılması İçin Gerekli Veriler - Devam • Havzayı temsil eden metroloji istasyonlarında mümkün olduğunca uzun süreli meteorolojik zaman serileri - yağış (saatlik) - sıcaklık (saatlik ve günlük maksimum ve minimumlarla birlikte) - nem (saatlik) - hava basıncı (saatlik) - rüzgar hızı ve yönü (saatlik) - buharlaşma (saatlik, mümkün değilse günlük) - bulutluluk (saatlik) - güneş ışıması (saatlik)

Havza Modellerinin Doğrulanması İçin Gerekli Veriler • Akarsulardaki debiler (günlük, mümkünse sürekli) • Akarsular ve göletlerle modellenen parametreler için su kalitesi değerler (Aylık) • Ürün desenine göre ürün verimleri

Hidrodinamik Modellerin Çalıştırılması İçin Gerekli Veriler • Ayrıntılı* batimetri • Kıyı bölgesinin büyük ölçekli/ayrıntılı topografyası • Modellenen ortama olan tüm girişlerin en azından günlük zaman çözünürlüğünde debileri. • Özellikle baraj göllerinde modellenen ortamın su kaynağı işletmesi ile ilgili günlük veriler * Eş derinlikler 1 m aralıklarla verilmeli, baraj göllerinde en azından ana akarsu girişlerinin yakın civarında batimetrik ölçümler yenilenmeli.

Hidrodinamik Modellerin Çalıştırılması İçin Gerekli Veriler-Devam • Eğer mümkünse uzun yıllar günlük verilerle doğrulanmış bir havza modelleme çalışmasından elde edilen anlık debiler.

Hidrodinamik Modellerin Çalıştırılması İçin Gerekli Veriler - Devam • Su ortamını temsil eden metroloji istasyonlarında mümkün olduğunca uzun süreli meteorolojik zaman serileri - yağış (saatlik) - sıcaklık (saatlik ve günlük maksimum ve minimumlarla birlikte) - nem (saatlik) - hava basıncı (saatlik) - rüzgar hızı ve yönü (saatlik) - buharlaşma (saatlik) - bulutluluk (saatlik) - güneş ışıması (saatlik)

Hidrodinamik Modellerinin Doğrulanması İçin Gerekli Veriler • Su seviyeleri (limnigraf - günlük, mümkünse sürekli) • Su sıcaklığı (günlük) • Akıntı hızı ve yönleri (mümkün olduğu kadar çok noktada ve yüksek zamansal çözünürlükte)

Su Kalitesi/Ekolojisi Modellerinin Çalıştırılması İçin Gerekli Veriler • Su ortamını temsil eden metroloji istasyonlarında mümkün olduğunca uzun süreli meteorolojik zaman serileri - hava sıcaklığı (günlük) - nem (günlük) - su sıcaklığı (günlük, mümkünse iyi doğrulanmış bir hidrodinamik modelden alınan sürekli simülasyon sonuçları) - rüzgar hızı (saatlik, mümkün değilse günlük ortalama) - buharlaşma (günlük) - bulutluluk (günlük) - güneş ışıması (saatlik)

Su Kalitesi/Ekolojisi Modellerinin Çalıştırılması İçin Gerekli Veriler - Devam • Ayrıntılı* batimetri • Kıyı bölgesinin büyük ölçekli/ayrıntılı topografyası • Modellenen ortama olan tüm girişlerin en azından günlük zaman çözünürlüğünde debileri. • Eğer mümkünse uzun yıllar günlük verilerle doğrulanmış bir havza modelinden elde edilen anlık debiler. * Eş derinlikler 1 m aralıklarla verilmeli, baraj göllerinde en azından ana akarsu girişlerinin yakın civarında batimetrik ölçümler yenilenmeli.

Su Kalitesi/Ekolojisi Modellerinin Çalıştırılması İçin Gerekli Veriler - Devam • Eğer mümkünse uzun yıllar günlük verilerle doğrulanmış bir havza modelleme çalışmasından elde edilen anlık debiler ve modellenen su kalitesi değişkenlerinin anlık değerleri. • Eğer böyle bir çalışma yoksa modellenen su ortamına giren başlıca akarsularda ölçülmüş günlük debiler ve su kalitesi değişkenlerinin aylık ölçümleri. • Modellenen su ortamına giren başlıca deşarjların (en azından diğerlerini temsil edici olanlarını) aylık debileri ve ilgili su kalitesi değişkenlerinin aylık ölçümleri.

Su Kalitesi/Ekolojisi Modellerinin Çalıştırılması İçin Gerekli Veriler - Devam • Eğer mümkünse uzun yıllar günlük verilerle doğrulanmış bir hidrodinamik modelleme çalışmasından elde edilen anlık debiler • Su kaynağının kullanımı ile ilgili bilgiler (işletme koşulları, su ürünleri avcılığı ve yetiştiriciliği operasyonları, vb. ) • Ortamın ekolojik yapısı (taban yapısı, çökellerin durumu, jeoloji, tabanda yaşayan canlılar sazlıklar, vb. ) • Yetiştirilen su ürünleri ile ilgili ayrıntılı veriler (örneğin yaş ve boy dağılımları, biyokütle, vb. )

Su Kalitesi/Ekolojisi Modellerinin Doğrulanması İçin Gerekli Veriler • Modellenen su kalitesi değişkenlerinin (parametrelerinin) en az bir yıl boyunca birden çok istasyonda, her istasyonda temsil edici birden çok derinlik için en az aylık ölçümü. • Bu ölçümlerin mümkünse bir hidrolojik yıla denk gelecek şekilde planlanmalı. • Modellenen değişkenlerle ilgili yerinde süreç hızları (örneğin fotosentez, solunum, fiksasyon vb) ölçümü.

TEMEL TAŞINIM DENKLEMLERİ

Tanımlar Temel boyutlar [M] Kütle [L] Uzunluk [T] Zaman Konsantrasyon Birim hacimdeki kütle [M∙L-3] Kütlesel debi Birim zamanda geçen kütle [M∙T-1] Akı Birim zamanda birim alandan geçen kütle [M∙L-2 ∙T-1]

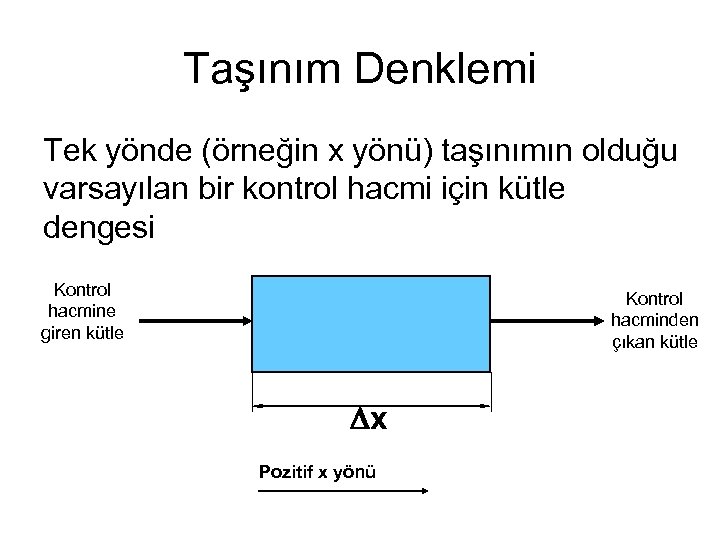Taşınım Denklemi Tek yönde (örneğin x yönü) taşınımın olduğu varsayılan bir kontrol hacmi için kütle dengesi Kontrol hacmine giren kütle Kontrol hacminden çıkan kütle Dx Pozitif x yönü

Taşınım Denklemi Bu durumda, kütle dengesi aşağıdaki gibi yazılabilir Denklem 1

Taşınım Denklemi Denklem 1’e daha yakından bir bakış Akı Konsantrasyon Alan Hacim [L 3] bölü zaman [L 2] [M∙L-2 ∙T-1] Akı Alan [M∙L-2 ∙T-1] [L 2] [M∙L-3 ∙T-1] [L 3]∙[M∙L-3∙T-1] = [M∙T-1] Kütle bölü zaman [L 2]∙[M∙L-2∙T-1] = [M∙T-1] Kütle bölü zaman

Taşınım Denklemi Birim hacimdeki kütle değişimi (Denklem 1’in iki tarafı da hacme bölünür) Denklem 2 Düzenleme yapılınca Denklem 3

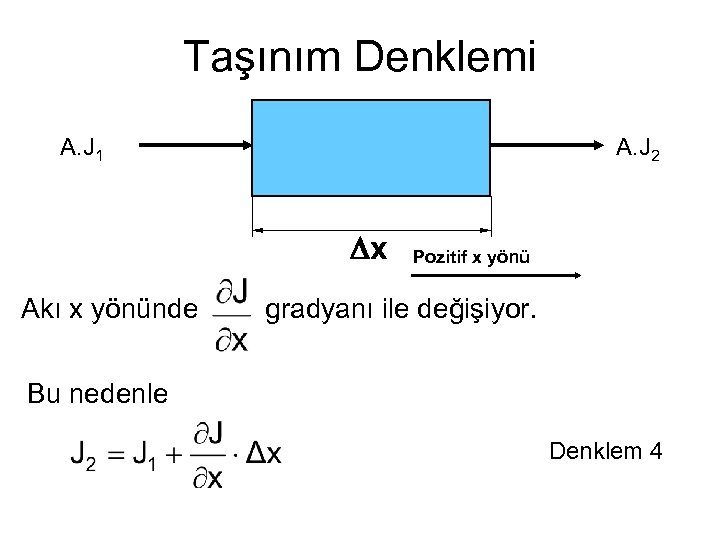Taşınım Denklemi A. J 1 A. J 2 Dx Akı x yönünde Pozitif x yönü gradyanı ile değişiyor. Bu nedenle Denklem 4

Taşınım Denklemi Denklem 3 Denklem 4 Denklem 5

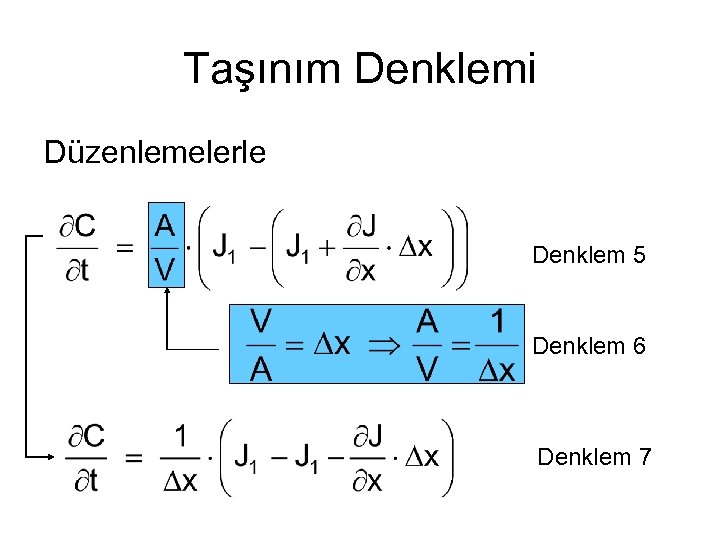Taşınım Denklemi Düzenlemelerle Denklem 5 Denklem 6 Denklem 7

Taşınım Denklemi Düzenlemelerle Denklem 7 Sonunda, x yönü için taşınım denkleminin en genel hali elde edilir. Denklem 8

Taşınım Denklemi Genel kütle dengesi ve taşınım kurallarının yöne göre değişmediği üç boyutlu bir uzayda yaşamaktayız. Bu nedenle x 1 = x x 2 = y Denklem 9 x 3 = z Denklem 10

Taşınım Denklemi • Taşınım denklemi, korunan bir iz maddesi için çıkarılmıştır. • Kontrol hacminin büyüklüğü, zamana göre sabittir. • Akı (J) herhangi bir süreç nedeniyle oluşmaktadır (akıntı, yayılma, vb. )

Öteleme (Adveksiyon) Akısı

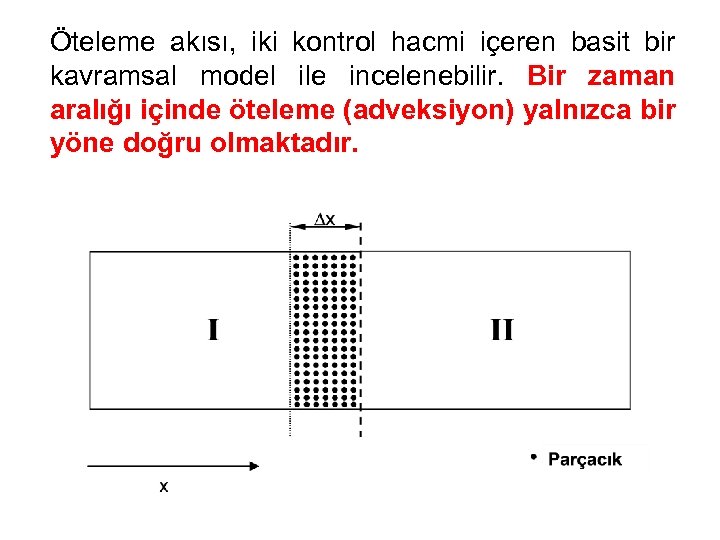Öteleme akısı, iki kontrol hacmi içeren basit bir kavramsal model ile incelenebilir. Bir zaman aralığı içinde öteleme (adveksiyon) yalnızca bir yöne doğru olmaktadır.

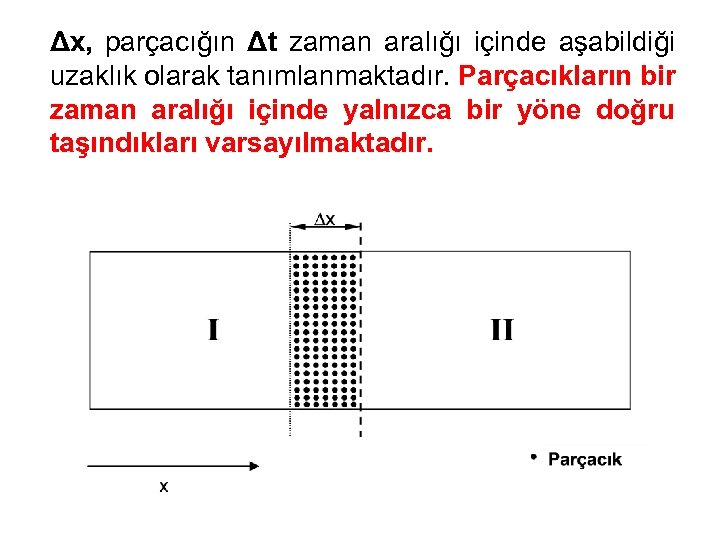Δx, parçacığın Δt zaman aralığı içinde aşabildiği uzaklık olarak tanımlanmaktadır. Parçacıkların bir zaman aralığı içinde yalnızca bir yöne doğru taşındıkları varsayılmaktadır.

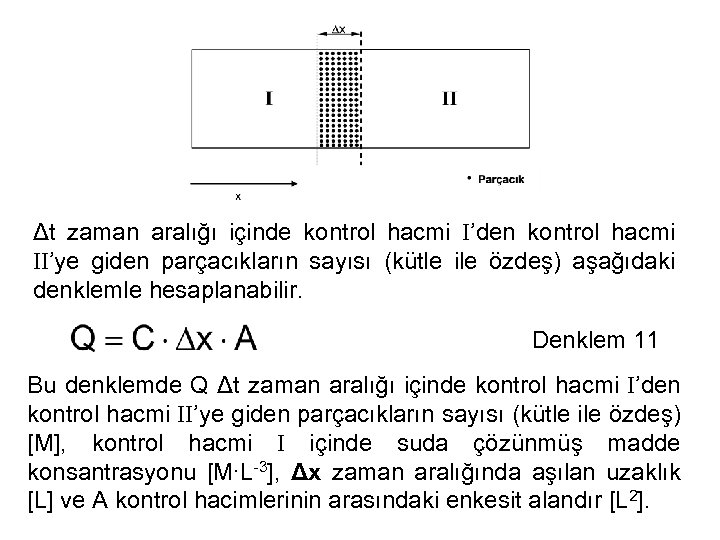Δt zaman aralığı içinde kontrol hacmi I’den kontrol hacmi II’ye giden parçacıkların sayısı (kütle ile özdeş) aşağıdaki denklemle hesaplanabilir. Denklem 11 Bu denklemde Q Δt zaman aralığı içinde kontrol hacmi I’den kontrol hacmi II’ye giden parçacıkların sayısı (kütle ile özdeş) [M], kontrol hacmi I içinde suda çözünmüş madde konsantrasyonu [M∙L-3], Δx zaman aralığında aşılan uzaklık [L] ve A kontrol hacimlerinin arasındaki enkesit alandır [L 2].

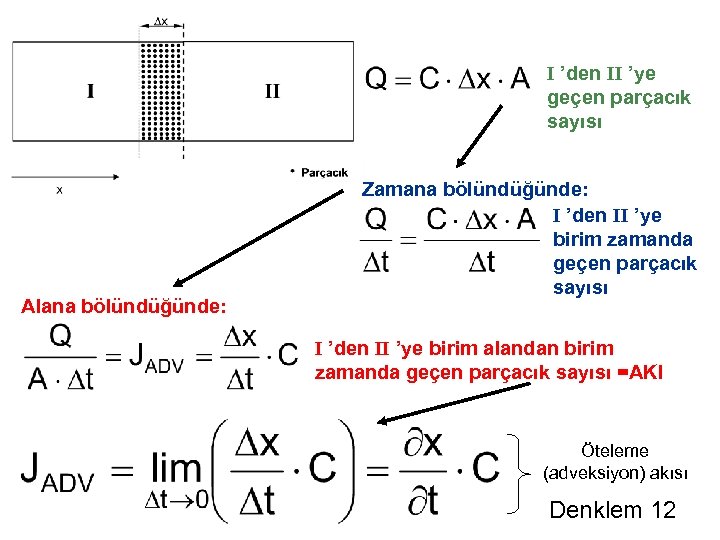I ’den II ’ye geçen parçacık sayısı Alana bölündüğünde: Zamana bölündüğünde: I ’den II ’ye birim zamanda geçen parçacık sayısı I ’den II ’ye birim alandan birim zamanda geçen parçacık sayısı =AKI Öteleme (adveksiyon) akısı Denklem 12

Öteleme (Adveksiyon) Akısı Denklem 12

Yayılma (Difüzyon) Akısı

Yayılma (difüzyon) akısı da basit bir kavramsal model ile incelenebilir. Kavramsal model iki kontrol hacmi içermektedir. Yayılma (difüzyon) bir zaman aralığı içinde iki yöne birden olabilmektedir.

Δx, parçacığın Δt zaman aralığı içinde aşabildiği uzaklık olarak tanımlanmaktadır. Parçacıkların bir zaman aralığında hem pozitif hem de negatif x yönünde hareket etmeleri mümkündür. Bu durumda Δt zaman aralığında, parçacık taşınımı olacak iki yön vardır.

Başka bir varsayım ise herhangi bir parçacığın Δt zaman aralığı içinde yönünü değiştirmeyeceği ve yalnızca pozitif veya negatif x yönüne hareket edeceğidir. Her zaman aralığında her parçacık pozitif veya negatif x yönlerinde ilerleme olasılığı aynıdır (%50). Bu nedenle yayılma (difüzyon) akısının biri kontrol hacmi I’den kontrol hacmi II’ye ve diğeri kontrol hacmi II’den kontrol hacmi I’e olmak üzere iki bileşeni vardır.

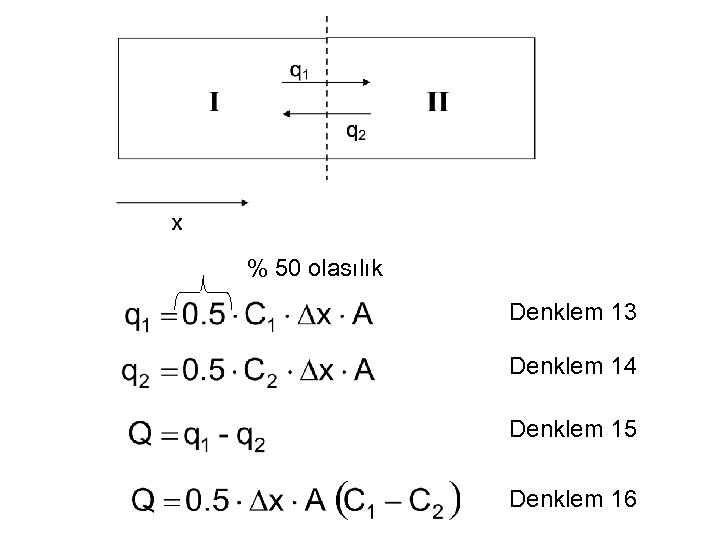% 50 olasılık Denklem 13 Denklem 14 Denklem 15 Denklem 16

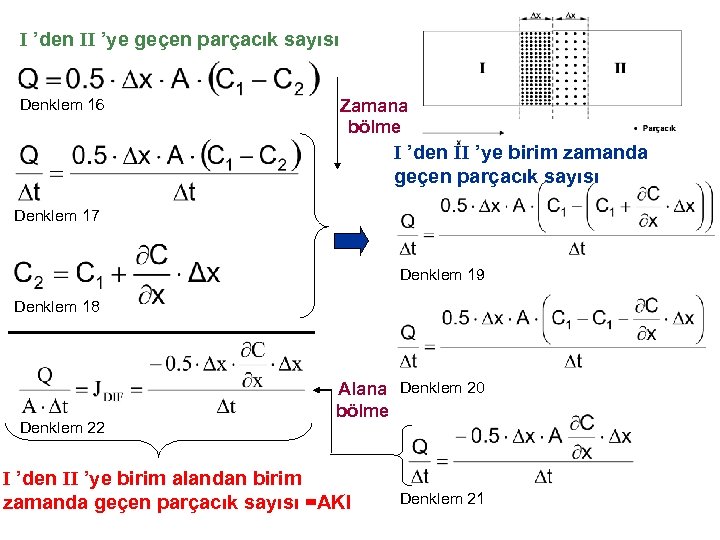I ’den II ’ye geçen parçacık sayısı Denklem 16 Zamana bölme I ’den II ’ye birim zamanda geçen parçacık sayısı Denklem 17 Denklem 19 Denklem 18 Denklem 22 Alana Denklem 20 bölme I ’den II ’ye birim alandan birim zamanda geçen parçacık sayısı =AKI Denklem 21

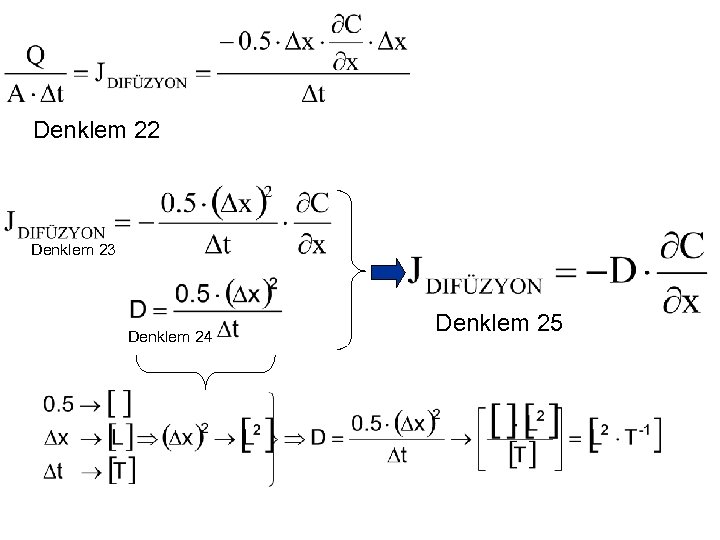Denklem 22 Denklem 23 Denklem 24 Denklem 25

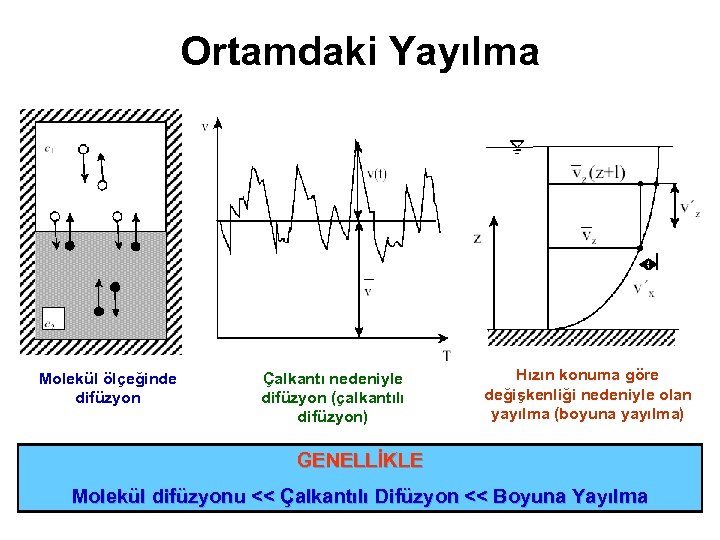Ortamdaki Yayılma Molekül ölçeğinde difüzyon Çalkantı nedeniyle difüzyon (çalkantılı difüzyon) Hızın konuma göre değişkenliği nedeniyle olan yayılma (boyuna yayılma) GENELLİKLE Molekül difüzyonu << Çalkantılı Difüzyon << Boyuna Yayılma

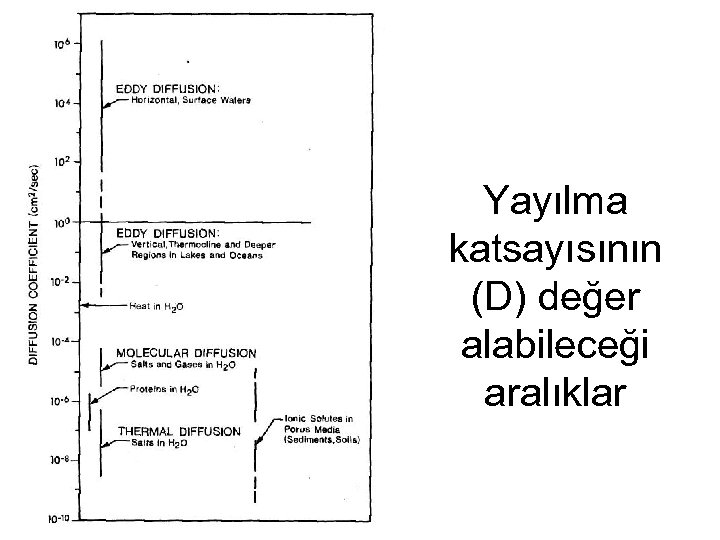Yayılma katsayısının (D) değer alabileceği aralıklar

Yayılma (Difüzyon) Akısı Denklem 25

KORUNAN BİR İZ MADDESİ İÇİN ÖTELEME-YAYILMA (ADVEKSİYON-DİFÜZYON) DENKLEMİ

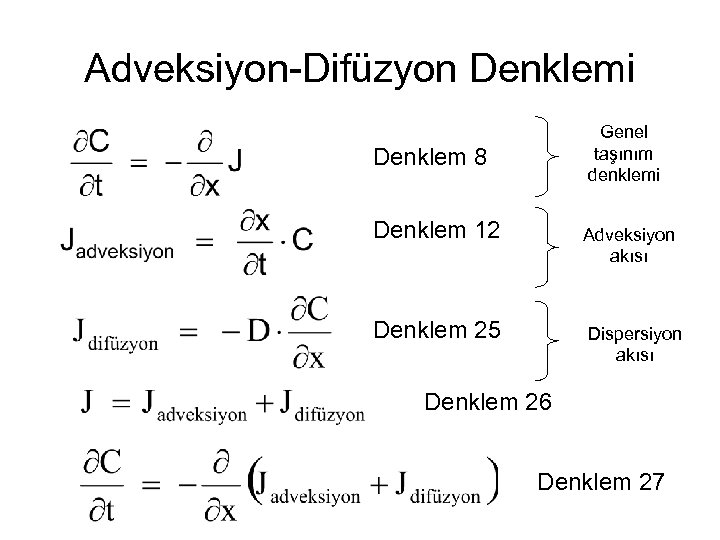Adveksiyon-Difüzyon Denklemi Genel taşınım denklemi Denklem 8 Denklem 12 Adveksiyon akısı Denklem 25 Dispersiyon akısı Denklem 26 Denklem 27

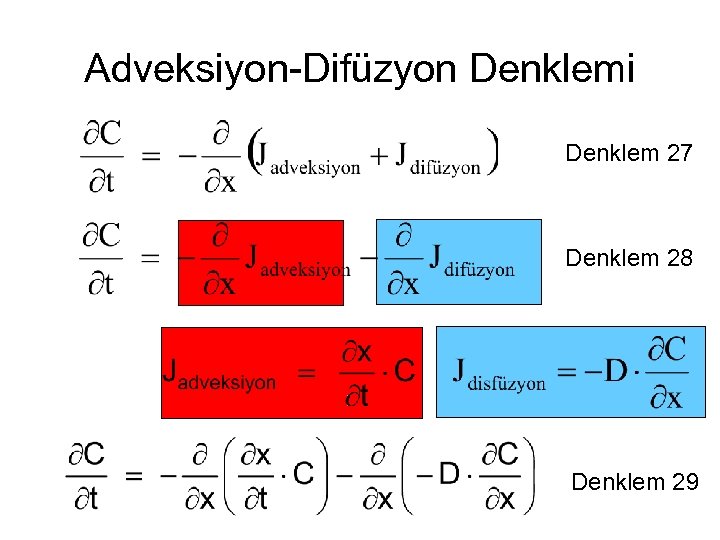Adveksiyon-Difüzyon Denklemi Denklem 27 Denklem 28 Denklem 29

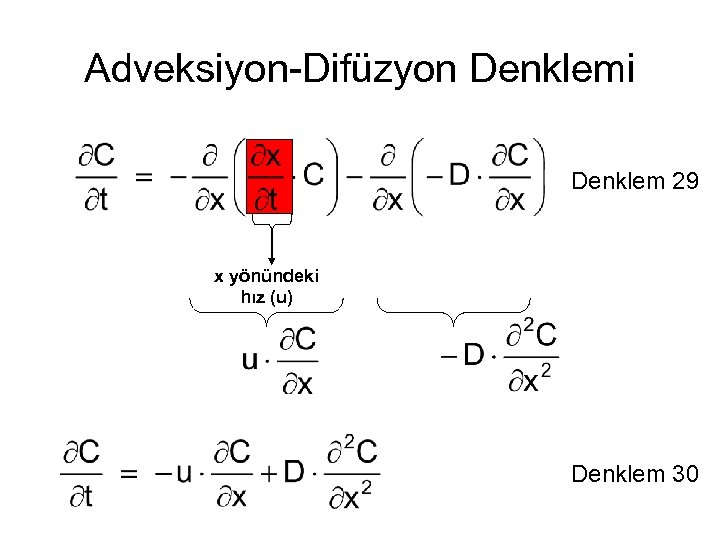Adveksiyon-Difüzyon Denklemi Denklem 29 x yönündeki hız (u) Denklem 30

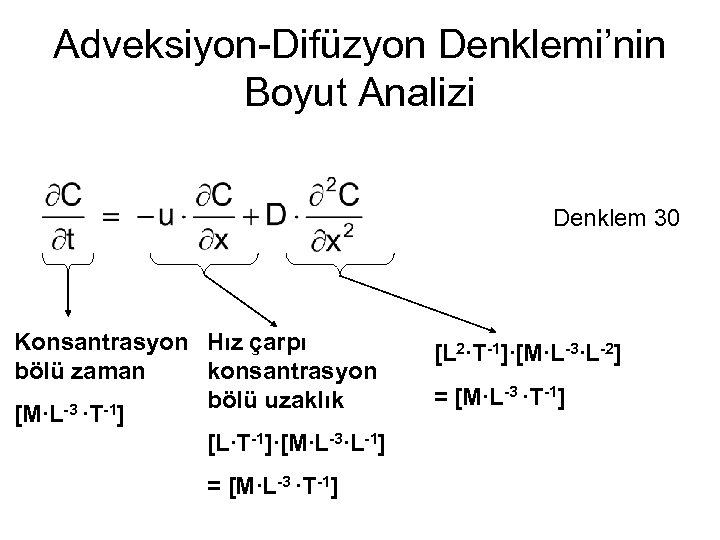Adveksiyon-Difüzyon Denklemi’nin Boyut Analizi Denklem 30 Konsantrasyon Hız çarpı bölü zaman konsantrasyon bölü uzaklık -3 ∙T-1] [M∙L [L∙T-1]∙[M∙L-3∙L-1] = [M∙L-3 ∙T-1] [L 2∙T-1]∙[M∙L-3∙L-2] = [M∙L-3 ∙T-1]

Adveksiyon-Difüzyon Denklemi Genel kütle dengesi ve taşınım kurallarının yöne göre değişmediği üç boyutlu bir uzayda yaşamaktayız. Bu nedenle x 1 = x, u 1 = u, D 1 = Dx x 2 = y, u 2 = v, D 2 = Dy Denklem 31 Denklem 32 x 3 = z, u 3 = w, D 3 = Dz

KORUNMAYAN BİR MADDE İÇİN ÖTELEME-YAYILMA (ADVEKSİYON-DİFÜZYON) DENKLEMİ

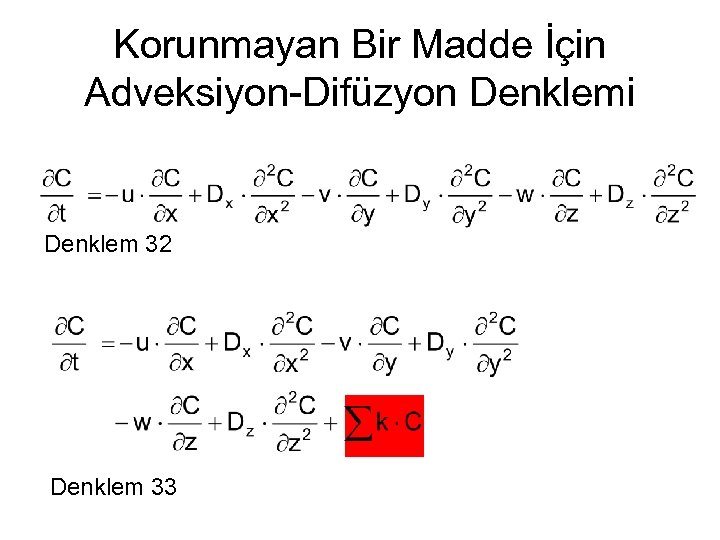Korunmayan Bir Madde İçin Adveksiyon-Difüzyon Denklemi Denklem 32 Denklem 33

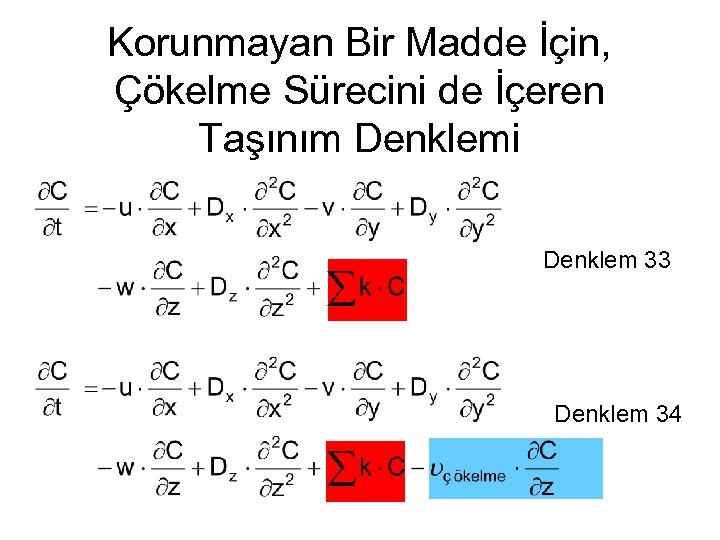Korunmayan Bir Madde İçin, Çökelme Sürecini de İçeren Taşınım Denklemi Denklem 33 Denklem 34

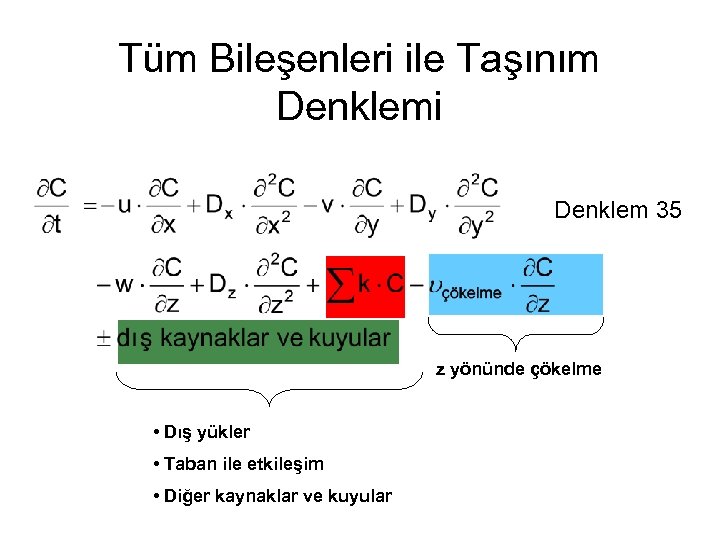Tüm Bileşenleri ile Taşınım Denklemi Denklem 35 z yönünde çökelme • Dış yükler • Taban ile etkileşim • Diğer kaynaklar ve kuyular

Bileşenlerin Boyut Analizi [M∙L-3]∙[T-1]=[M∙L-3 ∙T-1] [L∙T-1]∙[M∙L-3∙L-1]=[M∙L-3 ∙T-1] olarak verilmeli

Tüm Bileşenleri ile Taşınım Denklemi Denklem 35

Model Denklemlerinin Sayısal Çözümü

Sayısal Çözüm • Model uzayı sonlu sayıda homojen bölgeye ayrılır (konumsal ayrıklaştırma). • Zaman sonlu sayıda aralığa bölünür. (zamansal ayrıklaştırma). • Her zaman aralığı için her homojen bölgede kütle dengesi kurularak, taşınım denklemi sonlu sayıda cebirsel denkleme dönüştürülür.

Zamansal Ayrıklaştırma • Açık yöntemler Gelecek zaman aralığındaki çözüm, şimdiki zaman aralığındaki değerler ile hesaplanır. • Kapalı yöntemler Gelecek zaman aralığındaki çözüm, gelecek zaman aralığındaki değerler ile hesaplanır. • Yarı kapalı yöntemler Gelecek zaman aralığındaki çözüm, şimdiki ve gelecek zaman aralıklarındaki değerler ile hesaplanır.

Zamansal Ayrıklaştırma Birinci mertebe bozunma denklemi Açık çözüm

Zamansal Ayrıklaştırma Birinci mertebe bozunma denklemi Kapalı Çözüm

Zamansal Ayrıklaştırma Birinci mertebe bozunma denklemi Yarı Kapalı Çözüm

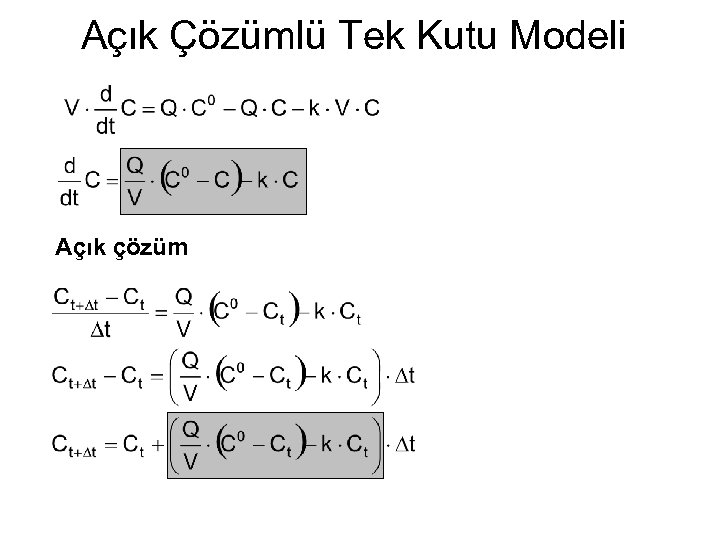Açık Çözümlü Tek Kutu Modeli Açık çözüm

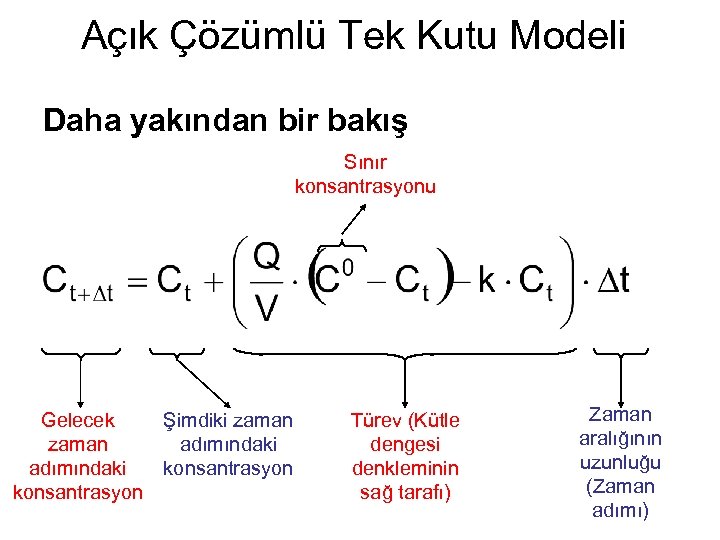Açık Çözümlü Tek Kutu Modeli Daha yakından bir bakış Sınır konsantrasyonu Gelecek zaman adımındaki konsantrasyon Şimdiki zaman adımındaki konsantrasyon Türev (Kütle dengesi denkleminin sağ tarafı) Zaman aralığının uzunluğu (Zaman adımı)

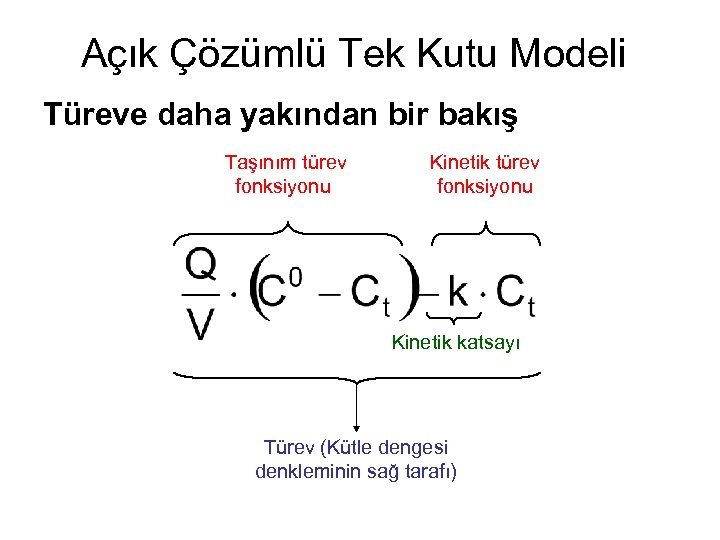Açık Çözümlü Tek Kutu Modeli Türeve daha yakından bir bakış Taşınım türev fonksiyonu Kinetik katsayı Türev (Kütle dengesi denkleminin sağ tarafı)

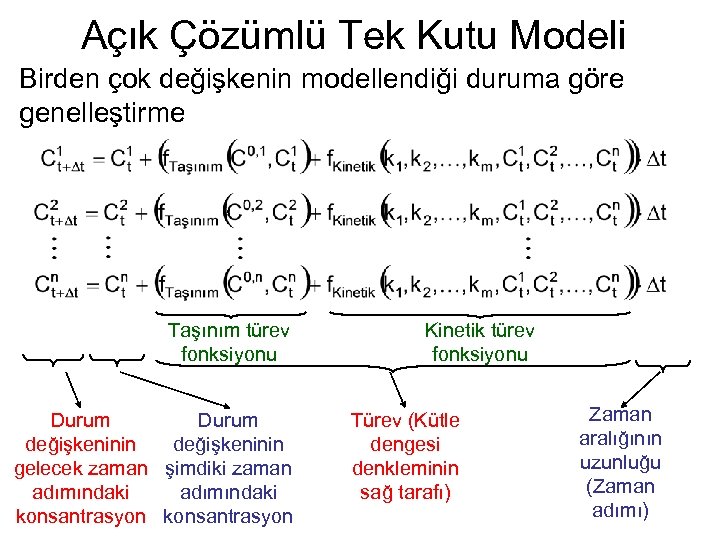Açık Çözümlü Tek Kutu Modeli Birden çok değişkenin modellendiği duruma göre genelleştirme Taşınım türev fonksiyonu Durum değişkeninin gelecek zaman şimdiki zaman adımındaki konsantrasyon Kinetik türev fonksiyonu Türev (Kütle dengesi denkleminin sağ tarafı) Zaman aralığının uzunluğu (Zaman adımı)

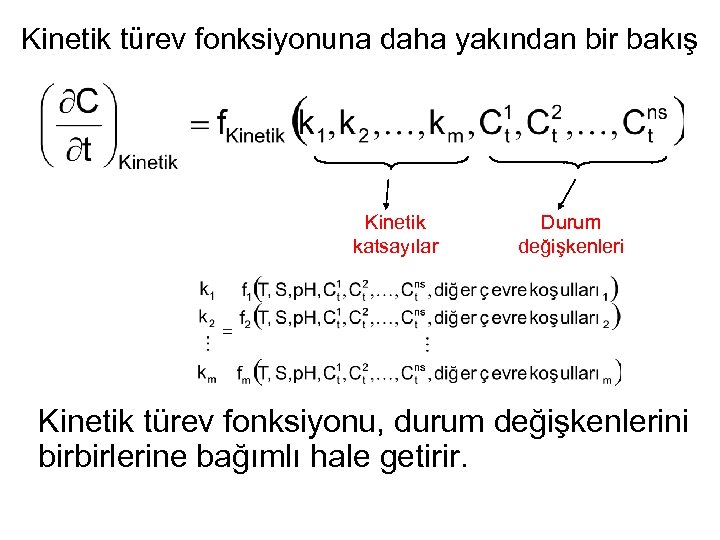Kinetik türev fonksiyonuna daha yakından bir bakış Kinetik katsayılar Durum değişkenleri Kinetik türev fonksiyonu, durum değişkenlerini birbirlerine bağımlı hale getirir.

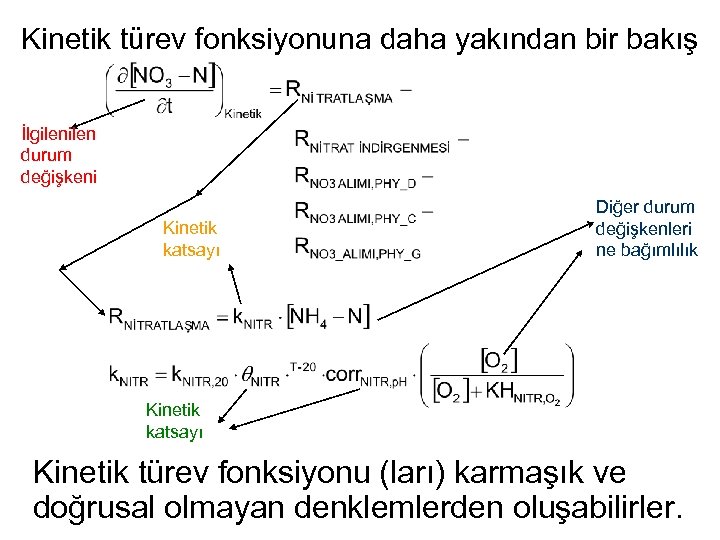Kinetik türev fonksiyonuna daha yakından bir bakış İlgilen durum değişkeni Kinetik katsayı Diğer durum değişkenleri ne bağımlılık Kinetik katsayı Kinetik türev fonksiyonu (ları) karmaşık ve doğrusal olmayan denklemlerden oluşabilirler.

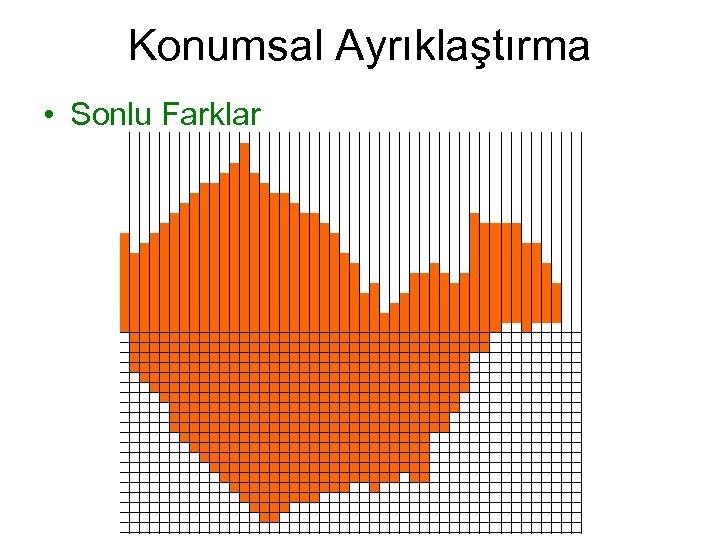Konumsal Ayrıklaştırma • Sonlu Farklar

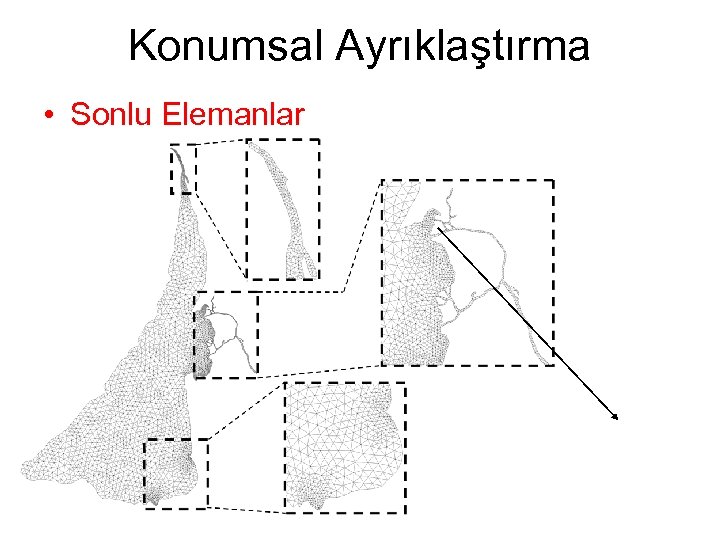Konumsal Ayrıklaştırma • Sonlu Elemanlar

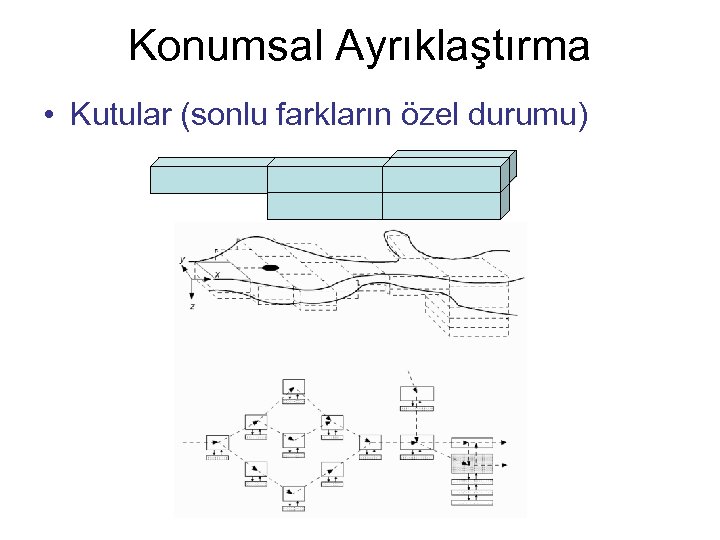Konumsal Ayrıklaştırma • Kutular (sonlu farkların özel durumu)

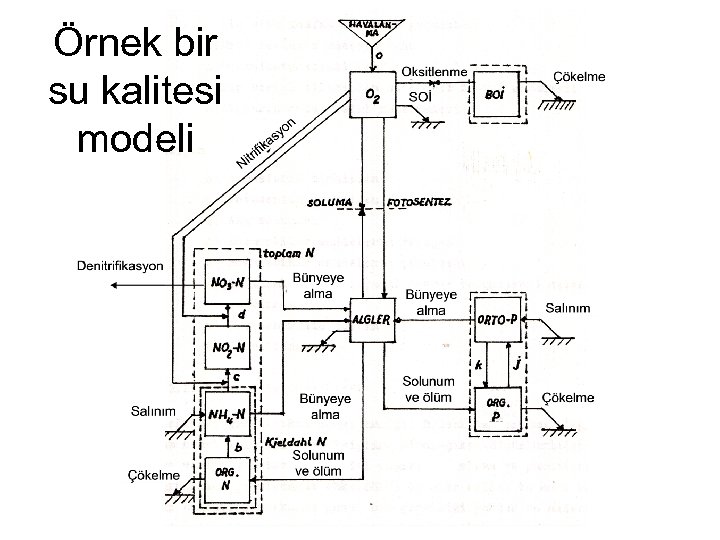Örnek bir su kalitesi modeli

Meraklısına … function [OUTMASSES, CONCENTRATIONS] =. . . WQ_ROUTE_1(IN_MASSES, OUTFLOWS, INITIAL_CONCENTRATIONS, . . . VOLUMES, NUM_TIME_STEPS, D_T, DYNAMIC_FORCINGS, . . . ELEVATION) NUM_S_VARS CONCENTRATIONS OUTMASSES = numel(INITIAL_CONCENTRATIONS); = ones(NUM_TIME_STEPS, NUM_S_VARS) * (-9999); CONCENTRATIONS(1, : ) = INITIAL_CONCENTRATIONS; OUTMASSES (1, : ) = INITIAL_CONCENTRATIONS. * OUTFLOWS(1); MASSES = INITIAL_CONCENTRATIONS. * VOLUMES (1); CONSTANTS = 0; OPTIONS = 1; for i = 2: NUM_TIME_STEPS FORCINGS(1: 9) = DYNAMIC_FORCINGS(i - 1, : ); FORCINGS(10) = ELEVATION; [KINETIC_DERIVS, SETTLING_DERIVS] =. . . WQ_KINETICS_1(CONCENTRATIONS(i - 1, : ), CONSTANTS, . . . FORCINGS, OPTIONS); %[KINETIC_DERIVS, SETTLING_DERIVS] =. . . % WQ_KINETICS_1_mex(CONCENTRATIONS(i - 1, : ), CONSTANTS, . . . % FORCINGS, OPTIONS); KINETIC_DERIVS = VOLUMES(i - 1). * KINETIC_DERIVS; MASSES = MASSES +. . . ((IN_MASSES(i-1, : ) - OUTMASSES(i-1, : ) +. . . KINETIC_DERIVS)) * D_T; CONCENTRATIONS(i, : ) = MASSES. / VOLUMES(i); for j = 1: NUM_S_VARS if (isnan(CONCENTRATIONS(i, j))) fprintf('nnn'); fprintf('--------------n'); fprintf('!!! ERROR IN WQ_ROUTE_1 !!!n'); fprintf('--------------n'); fprintf('State variable no : %dn' , j); fprintf('VOLUMES(i-1) : %fn' , VOLUMES(i-1)); fprintf('VOLUMES(i) : %fn' , VOLUMES(i)); fprintf('IN_MASSES(i-1) : %fn' , IN_MASSES(i-1, : )); fprintf('OUTMASSES(i-1) : %fn' , OUTMASSES(i-1, : )); fprintf('KINETIC_DERIVS : %fn' , KINETIC_DERIVS); fprintf('MASSES (j) : %fn' , MASSES (j)); fprintf('KINETIC_DERIVS(j) : %fnn', KINETIC_DERIVS(j)); error('Concentration is not a number'); end if (CONCENTRATIONS(i, j) < 1. 0 E-10) CONCENTRATIONS(i, j) = 1. 0 E-10; end MASSES OUTMASSES end = CONCENTRATIONS(i, : ). * VOLUMES(i); (i, : ) = CONCENTRATIONS(i, : ). * OUTFLOWS(i);

function [DERIVS, SETTLING_DERIVS] =. . . WQ_KINETICS_1(S_VARS, CONSTANTS, FORCINGS, OPTIONS) NUM_SVAR = numel(S_VARS); DERIVS = ones(1, NUM_SVAR) * (-9999); SETTLING_DERIVS = ones(1, NUM_SVAR) * (-9999); PHYC ORGN NH 4 N NO 2 N NO 3 N ORGP PO 4 P CBOD DOXY TEMP = = = = = K_H_ORGN_MINER = 0. 2; K_H_ORGN_SETTL = 0. 2; K_H_ORGP_MINER = 0. 05; K_H_ORGP_SETTL = 0. 05; K_H_CBOD_MINER = 1. 0; K_H_DOXY_MINER = 1. 0; K_H_CBOD_SETTL = 1. 0; S_VARS(1); S_VARS(2); S_VARS(3); S_VARS(4); S_VARS(5); S_VARS(6); S_VARS(7); S_VARS(8); S_VARS(9); S_VARS(10); K_DENIT = 0. 8; THETA_K_DENIT = 1. 02; K_HS_DOXY_DENIT = 1. 0; % Air temperature (degrees Celcisus) AIR_TEMP = FORCINGS(1); C_TO_CHLA N_TO_C P_TO_C O 2_TO_C K_G_20 THETA_K_G K_R_20 THETA_K_R V_S_A_20 THETA_V_S_A_20 K_H_N_A K_H_P_A = = = 30; 0. 25; 0. 05; 2. 66; 2. 0; 1. 066; 0. 05; 1. 045; 0. 3; 1. 03; 0. 2; 0. 05; K_MIN_N THETA_K_MIN_N V_S_N_20 THETA_V_S_N_20 = = 0. 3; 1. 04; 0. 5; 1. 04; K_NITR_1_20 THETA_NITR_1 K_H_NH 4 N_NITR_1 K_H_DOXY_NITR_1 K_H_PREF_NH 4 N_GROWTH_NH 4 N = = = 0. 5; 1. 045; 0. 6; 1. 5; 0. 1; % Current velocity (m/s) CURRENT_VEL = FORCINGS(7); K_NITR_2_20 THETA_NITR_2 K_H_NO 2 N_NITR_2 K_H_DOXY_NITR_2 = = 5. 0; 1. 045; 0. 1; 1. 5; % Background light extinction of water (m^-1) K_E_W = FORCINGS(9); K_MIN_P THETA_K_MIN_P V_S_P_20 THETA_V_S_P_20 = = 0. 3; 1. 04; 0. 5; 1. 04; K_MIN_C THETA_K_MIN_C V_S_C_20 THETA_V_S_C_20 = = 0. 3; 1. 04; 0. 5; 1. 04; K_A_20 THETA_K_A_20 = 0. 5; = 1. 045; %I_S K_HS_LIGHT W_TYPE = 100000; = 3000; = 1; % Relative hummidity R_H = FORCINGS(2); % ----------------------------------% PROCESS RATE CALCULATION FOR TEMPERATURE % ----------------------------------C_P = 1000000; RHO = 1; SIGMA = 11. 7 E-8; %Stefan-Bolzman constant cal / (cm^2 * d * K^4) A = 0. 6; R_L = 0. 03; EMISS_WATER = 0. 97; C_1 = 0. 47; %Bowen ratio, mm. Hg C-1 % Calculate the saturation vapour pressure E_SAT = 4. 596 * exp((17. 27 * AIR_TEMP) / (237. 3 + AIR_TEMP)); E_AIR = R_H * E_SAT; % T_D = 237. 3 / (17. 27/log(E_AIR / 4. 596)); E_S = 4. 596 * exp((17. 27 * TEMP) / (237. 3 + TEMP)); HEAT_CAP = RHO * C_P * H; F_UW = 19. 0 + (0. 95 * WIND_SPEED); NET_SOLAR_RAD = J_SN / HEAT_CAP; % Shortwave solar radiaton (MJ. m^2. day^-1) J_SN = FORCINGS(3) * 238845. 8966275; ATMOSPHERIC_LONG_WAVE_RAD = (SIGMA / HEAT_CAP) *. . . ((AIR_TEMP+ 273). ^4) * (A + 0. 031 *(E_AIR. ^0. 5)) * (1 - R_L); % Wind speed (m/s) WIND_SPEED = FORCINGS(4); WATER_LONG_WAVE_RAD = EMISS_WATER *. . . (SIGMA / HEAT_CAP) * ((AIR_TEMP + 273). ^4); FRAC_L = FORCINGS(5); % Depth(m) H = FORCINGS(6); CONDUCTION = C_1 * F_UW * (TEMP - AIR_TEMP); EVAPORATION = F_UW * (E_S - E_AIR); % ----------------------------------% END OF PROCESS RATE CALCULATION FOR TEMPERATURE % ----------------------------------- if (H < 0. 1) H = 0. 1; end % Salinity (ppt) SALT = FORCINGS(8); % Elevation ELEV = FORCINGS(10); % ----------------------------------% PROCESS RATE CALCULATIONS FOR PHYTOPLAKTON % ----------------------------------if (OPTIONS == 1) % Calculate the TEMPerature limitation LIM_TEMP_A = (THETA_K_G. ^(TEMP - 20)); % Calculate INORG_SOLID DETRITUS CHLA the light limitation = 0; = (PHYC / C_TO_CHLA) * 1000; K_E_P = K_E_W + (0. 052 * INORG_SOLID) + (0. 174 * DETRITUS); K_E = K_E_P + (0. 0088 * CHLA) + (0. 054 *(CHLA. ^ (2/3))); %238845. 8966275 (MJ ---> Calories) I_A = 0. 45 * FORCINGS(9) * 238845. 8966275; %ALPHA_0 = (I_A / I_S); %ALPHA_1 = (I_A / I_S) * exp(-K_E * H); if (OPTIONS == 1) TEMP = 5. 0 + (0. 75 * AIR_TEMP); else TEMP = 10; end %LIM_LIGHT_A = ((2. 718 * FRAC_L). / (K_E * H)) *. . . % (exp(-ALPHA_1)-exp(-ALPHA_0)); %if (LIM_LIGHT_A < 0. 5) % LIM_LIGHT_A = 0. 5; %end AVG_LIGHT = (I_A / (H * K_E)) * (1 - exp(-K_E * H)); LIM_LIGHT_A = AVG_LIGHT / (AVG_LIGHT + K_HS_LIGHT); 2

% ----------------------------------% PROCESS RATE CALCULATION FOR TEMPERATURE % ----------------------------------C_P = 1000000; RHO = 1; SIGMA = 11. 7 E-8; %Stefan-Bolzman constant cal / (cm^2 * d * K^4) A = 0. 6; R_L = 0. 03; EMISS_WATER = 0. 97; C_1 = 0. 47; %Bowen ratio, mm. Hg C-1 % Calculate the saturation vapour pressure E_SAT = 4. 596 * exp((17. 27 * AIR_TEMP) / (237. 3 + AIR_TEMP)); E_AIR = R_H * E_SAT; % T_D = 237. 3 / (17. 27/log(E_AIR / 4. 596)); E_S = 4. 596 * exp((17. 27 * TEMP) / (237. 3 + TEMP)); RESPIRATION = K_R_20 * (THETA_K_R. ^(TEMP - 20)) * PHYC; SETTLING_A = (V_S_A_20 / H) * (THETA_V_S_A_20. ^(TEMP - 20)) * PHYC; % ----------------------------------% END OF PROCESS RATE CALCULATIONS FOR PHYTOPLAKTON % --------------------------------------------------------------------% PROCESS RATE CALCULATIONS FOR NITROGEN CYCLE % ----------------------------------% Organic Nitrogen RESPIRATION_N = N_TO_C * RESPIRATION; LIM_ORGN_MINER = ORGN / (ORGN + K_H_ORGN_MINER); LIM_ORGN_SETTL = ORGN / (ORGN + K_H_ORGN_SETTL); MINERALIZATION_N = K_MIN_N * (THETA_K_MIN_N. ^(TEMP - 20)) LIM_ORGN_MINER * ORGN; HEAT_CAP = RHO * C_P * H; F_UW = 19. 0 + (0. 95 * WIND_SPEED); SETTLING_N NET_SOLAR_RAD = J_SN / HEAT_CAP; ATMOSPHERIC_LONG_WAVE_RAD = (SIGMA / HEAT_CAP) *. . . ((AIR_TEMP+ 273). ^4) * (A + 0. 031 *(E_AIR. ^0. 5)) * (1 - R_L); % NH 4 N LIM_TEMP_NITR_1 = THETA_NITR_1. ^(TEMP - 20); LIM_NH 4 N_NITR_1 = NH 4 N / (K_H_NH 4 N_NITR_1 + NH 4 N); LIM_DOXY_NITR_1 = DOXY / (K_H_DOXY_NITR_1 + DOXY); WATER_LONG_WAVE_RAD = EMISS_WATER *. . . (SIGMA / HEAT_CAP) * ((AIR_TEMP + 273). ^4); NITRIFICATION_1 = K_NITR_1_20 * LIM_TEMP_NITR_1 *. . LIM_NH 4 N_NITR_1 * LIM_DOXY_NITR_1; CONDUCTION = C_1 * F_UW * (TEMP - AIR_TEMP); EVAPORATION = F_UW * (E_S - E_AIR); % ----------------------------------% END OF PROCESS RATE CALCULATION FOR TEMPERATURE % ----------------------------------- *. . . SEDIMENT_RELEASE_N = 0; % ----------------------------------% PROCESS RATE CALCULATIONS FOR PHYTOPLAKTON % ----------------------------------if (OPTIONS == 1) % Calculate the TEMPerature limitation LIM_TEMP_A = (THETA_K_G. ^(TEMP - 20)); % Calculate INORG_SOLID DETRITUS CHLA the light limitation = 0; = (PHYC / C_TO_CHLA) * 1000; K_E_P = K_E_W + (0. 052 * INORG_SOLID) + (0. 174 * DETRITUS); K_E = K_E_P + (0. 0088 * CHLA) + (0. 054 *(CHLA. ^ (2/3))); AVG_LIGHT = (I_A / (H * K_E)) * (1 - exp(-K_E * H)); LIM_LIGHT_A = AVG_LIGHT / (AVG_LIGHT + K_HS_LIGHT); LIM_LIGHT_A = real(LIM_LIGHT_A); % Calculate the nutrient limitation DIN = NH 4 N + NO 3 N; LIM_NUT_A = min((DIN / (K_H_N_A + DIN)), (PO 4 P / (K_H_P_A + PO 4 P))); GROWTH = K_G_20 * LIM_TEMP_A * min(LIM_LIGHT_A, LIM_NUT_A) * PHYC; else GROWTH = 0; V_S_A_20 = 1. 0; K_R_20 = K_R_20 * 2; end = (V_S_N_20 / H) * (THETA_V_S_N_20. ^(TEMP - 20)) *. . . LIM_ORGN_SETTL * ORGN; PREF_NH 4 N_GROWTH = NH 4 N / (NH 4 N + K_H_PREF_NH 4 N_GROWTH_NH 4 N); GROWTH_NN 4 N = N_TO_C * GROWTH * PREF_NH 4 N_GROWTH; % NO 2 N LIM_TEMP_NITR_2 = THETA_NITR_2. ^(TEMP - 20); LIM_NO 2 N_NITR_2 = NO 2 N / (K_H_NO 2 N_NITR_2 + NH 4 N); LIM_DOXY_NITR_2 = DOXY / (K_H_DOXY_NITR_2 + DOXY); NITRIFICATION_2 = K_NITR_2_20 * LIM_TEMP_NITR_2 *. . LIM_NO 2 N_NITR_2 * LIM_DOXY_NITR_2; % NO 3 N LIM_TEMP_DENIT = THETA_K_DENIT. ^(TEMP - 20); LIM_O 2_DENIT = K_HS_DOXY_DENIT / (DOXY + K_HS_DOXY_DENIT); GROWTH_NO 3 N = N_TO_C * GROWTH * (1 - PREF_NH 4 N_GROWTH); DENITRIFICATION = K_DENIT * LIM_O 2_DENIT * LIM_TEMP_DENIT; % ----------------------------------% END OF PROCESS RATE CALCULATIONS FOR NITROGEN CYCLE % --------------------------------------------------------------------% PROCESS RATE CALCULATIONS FOR PHOSPHORUS CYCLE % ----------------------------------% Organic Phoshorus LIM_ORGP_MINER = ORGP / (ORGP + K_H_ORGP_MINER); LIM_ORGP_SETTL = ORGP / (ORGP + K_H_ORGP_SETTL); RESPIRATION_P = P_TO_C * RESPIRATION; MINERALIZATION_P = K_MIN_P * (THETA_K_MIN_P. ^(TEMP - 20)) LIM_ORGP_MINER * ORGP; SETTLING_P *. . . = (V_S_P_20 / H) * (THETA_V_S_P_20. ^(TEMP - 20)) *. . . LIM_ORGP_SETTL * ORGP; % Phosphate Phosphorus SEDIMENT_RELEASE_P = 0; GROWTH_P = P_TO_C * GROWTH; % ----------------------------------% END OF PROCESS RATE CALCULATIONS FOR PHOSPHORUS CYCLE % -----------------------------------

% ----------------------------------% PROCESS RATE CALCULATIONS FOR ORGANIC MATTER AND DISSOLVED OXYGEN % ----------------------------------% Carbonaceous BOD LIM_CBOD_MINER = CBOD / (CBOD + K_H_CBOD_MINER); LIM_CBOD_SETTL = CBOD / (CBOD + K_H_CBOD_SETTL); LIM_O 2_MINER = DOXY / (DOXY + K_H_DOXY_MINER); % Phosphate Phosphorus DERIVS(7) = MINERALIZATION_P + SEDIMENT_RELEASE_P - GROWTH_P; SETTLING_DERIVS(7) = 0; MINERALIZATION_O 2 = K_MIN_C * (THETA_K_MIN_C. ^(TEMP - 20)) LIM_CBOD_MINER * LIM_O 2_MINER * CBOD; % Dissolved Oxygen DERIVS(9) = REAERATION - MINERALIZATION_O 2 - SOD + GROWTH_O 2 -. . . RESPIRATION_O 2 - NITRIFICATION_1_O 2 - NITRIFICATION_2_O 2; *. . . SETTLING_O 2 = (V_S_C_20 / H) * (THETA_V_S_C_20. ^(TEMP - 20)) *. . . LIM_CBOD_SETTL * CBOD; % Dissolved Oxygen if (OPTIONS == 1) C_SAT_O 2 = DO_SATURATION(TEMP, SALT, ELEV); if (K_A_20 > 0) K_A = K_A_20 * (THETA_K_A_20. ^(TEMP - 20)); else KA_WIND = KAWIND (WIND_SPEED, TEMP, AIR_TEMP, H, WTYPE); KA_HYDRA = KAHYDRA(H, CURRENT_VEL, (TEMP - 20)); if (KA_WIND > KA_HYDRA) K_A = KA_WIND; else K_A = KA_HYDRA; end REAERATION = K_A * (C_SAT_O 2 - DOXY); else REAERATION = 0; end SOD GROWTH_O 2 RESPIRATION_O 2 NITRIFICATION_1_O 2 NITRIFICATION_2_O 2 = = = 0; O 2_TO_C * GROWTH; O 2_TO_C * RESPIRATION; 3. 43 * NITRIFICATION_1; 1. 14 * NITRIFICATION_2; % ----------------------------------% PROCESS RATE CALCULATIONS FOR ORGANIC MATTER AND DISSOLVED OXYGEN % ----------------------------------% Phytoplankton DERIVS(1) = GROWTH - RESPIRATION - SETTLING_A; SETTLING_DERIVS(1) = SETTLING_A; % Organic Nitrogen DERIVS(2) = RESPIRATION_N - MINERALIZATION_N - SETTLING_N; SETTLING_DERIVS(2) = SETTLING_N; % Ammonia Nitrogen DERIVS(3) = MINERALIZATION_N - NITRIFICATION_1 +. . . SEDIMENT_RELEASE_N - GROWTH_NN 4 N; SETTLING_DERIVS(3) = 0; % Nitrite Nitrogen DERIVS(4) = NITRIFICATION_1 - NITRIFICATION_2; SETTLING_DERIVS(4) = 0; % Nitrate Nitrogen DERIVS(5) = NITRIFICATION_2 - GROWTH_NO 3 N - DENITRIFICATION; SETTLING_DERIVS(5) = 0; % Organic Phosphorus DERIVS(6) = RESPIRATION_P - MINERALIZATION_P - SETTLING_P; SETTLING_DERIVS(6) = SETTLING_P; % Carbonaceous BOD DERIVS(8) = RESPIRATION_O 2 - MINERALIZATION_O 2 - SETTLING_O 2; SETTLING_DERIVS(8) = SETTLING_O 2; SETTLING_DERIVS(9) = 0; % Temperature if (OPTIONS == 1) DERIVS(10) = NET_SOLAR_RAD + ATMOSPHERIC_LONG_WAVE_RAD -. . . WATER_LONG_WAVE_RAD - CONDUCTION - EVAPORATION; else DERIVS(10) = 0; end SETTLING_DERIVS(10) = 0; if (sum(isnan(DERIVS)) > 0) fprintf('nnn'); fprintf('---------------n'); fprintf('!!! ERROR IN WQ_KINETICS_1 !!!n'); fprintf('---------------n'); fprintf('Derivative for PHYC : %fn', DERIVS(1)); fprintf(' PHYC : %fn', PHYC); fprintf('Derivative for ORGN : %fn', DERIVS(2)); fprintf(' ORGN : %fn', ORGN); fprintf('Derivative for NH 4 N : %fn', DERIVS(3)); fprintf(' NH 4 N : %fn', NH 4 N); fprintf('Derivative for NO 2 N : %fn', DERIVS(4)); fprintf(' NO 2 N : %fn', NO 2 N); fprintf('Derivative for NO 3 N : %fn', DERIVS(5)); fprintf(' NO 3 N : %fn', NO 3 N); fprintf('Derivative for ORGP : %fn', DERIVS(6)); fprintf(' ORGP : %fn', ORGP); fprintf('Derivative for PO 4 P : %fn', DERIVS(7)); fprintf(' PO 4 P : %fn', PO 4 P); fprintf('Derivative for CBOD : %fn', DERIVS(8)); fprintf(' CBOD : %fn', CBOD); fprintf('Derivative for DOXY : %fn', DERIVS(9)); fprintf(' DOXY : %fn', DOXY); fprintf('Derivative for TEMP : %fn', DERIVS(10)); fprintf(' TEMP : %fn', TEMP); fprintf('n'); fprintf('GROWTH fprintf(' K_G_20 : %fn', GROWTH); : %fn' , K_G_20); if (OPTIONS == 1) fprintf(' LIM_TEMP_A : %fn' , LIM_TEMP_A); fprintf(' THETA_K_G : %fn', FRAC_L); fprintf(' TEMP : %fn', TEMP); fprintf(' AIR_TEMP : %fn', AIR_TEMP); fprintf('n'); fprintf(' LIM_NUT_A : %fn' , LIM_NUT_A); fprintf('n') fprintf(' LIM_LIGHT_A : %fn' , LIM_LIGHT_A); fprintf(' FRAC_L : %fn', FRAC_L); fprintf(' K_E : %fn', K_E); fprintf(' H : %fn', H); fprintf(' ALPHA_1 : %fn', ALPHA_1); fprintf(' ALPHA_0 : %fn', ALPHA_0); fprintf(' exp(-ALPHA_1)-exp(-ALPHA_0) : %fn', . . . exp(-ALPHA_1)-exp(-ALPHA_0));

fprintf(' I_A : %fn', I_A); end fprintf('n'); fprintf('RESPIRATION fprintf('SETTLING_A : %fn', RESPIRATION); : %fn', SETTLING_A); fprintf('MINERALIZATION_N fprintf('RESPIRATION_N fprintf('MINERALIZATION_N fprintf('SETTLING_N : : %fn', MINERALIZATION_N); RESPIRATION_N); MINERALIZATION_N); SETTLING_N); fprintf('MINERALIZATION_N fprintf('NITRIFICATION_1 fprintf('SEDIMENT_RELEASE_N fprintf('GROWTH_NN 4 N; : : %fn', MINERALIZATION_N); NITRIFICATION_1); SEDIMENT_RELEASE_N); GROWTH_NN 4 N); fprintf('NITRIFICATION_1 fprintf('NITRIFICATION_2 : %fn', NITRIFICATION_1); : %fn', NITRIFICATION_2); fprintf('NITRIFICATION_2 fprintf('GROWTH_NO 3 N fprintf('DENITRIFICATION : %fn', NITRIFICATION_2); : %fn', GROWTH_NO 3 N); : %fn', DENITRIFICATION); fprintf('RESPIRATION_P fprintf('MINERALIZATION_P fprintf('SETTLING_P : %fn', RESPIRATION_P); : %fn', MINERALIZATION_P); : %fn', SETTLING_P); fprintf('MINERALIZATION_P fprintf('SEDIMENT_RELEASE_P fprintf('GROWTH_P : %fn', MINERALIZATION_P); : %fn', SEDIMENT_RELEASE_P); : %fn', GROWTH_P); fprintf('RESPIRATION fprintf('MINERALIZATION_O 2 fprintf('SETTLING_O 2; : %fn', RESPIRATION); : %fn', MINERALIZATION_O 2); : %fn', SETTLING_O 2); fprintf('REAERATION fprintf('MINERALIZATION_O 2 fprintf('SOD fprintf('GROWTH_O 2 fprintf('RESPIRATION_O 2 fprintf('NITRIFICATION_1_O 2 fprintf('NITRIFICATION_2_O 2 : : : : %fn', %fn', REAERATION); MINERALIZATION_O 2); SOD); GROWTH_O 2); RESPIRATION_O 2); NITRIFICATION_1_O 2); NITRIFICATION_2_O 2); fprintf('NET_SOLAR_RAD fprintf('ATMOSPHERIC_LONG_WAVE_RAD fprintf('WATER_LONG_WAVE_RAD fprintf('CONDUCTION fprintf('EVAPORATION : : : %fn', %fn', NET_SOLAR_RAD); ATMOSPHERIC_LONG_WAVE_RAD); WATER_LONG_WAVE_RAD); CONDUCTION); EVAPORATION); fprintf('n'); fprintf('OPITONS : %dn', OPTIONS); error('One or more of the kinetic derivatives is not a numbern'); end

SU KALİTESİ MODELLERİ İÇİN MODEL GİRDİLERİ ve ÇIKTILARI

TANIMLAR • Modelleme Yazılımı Matematiksel bir modelin; model girdilerinin oluşturulması, hesap ve model çıktılarının oluşturulup görselleştirilmesi için gerekli işlemleri yürüten bilgisayar programı ya da programları • Benzetim (Simülasyon) Modelleme yazılımının çalıştırılarak gerçek sistemdeki süreçlerin, bilgisayar ortamında canlandırılması

TANIMLAR • Benzetim süresi Dinamik modellerde benzetimin yapıldığı süre (Örneğin 1 Ocak 1998’den 1 Ocak 2000’e kadar iki yıl) • Hesap süresi (Bilgisayar süresi) Benzetimin tamamlanması için benzetimin yapıldığı bilgisayarın ihtiyacı olan süre

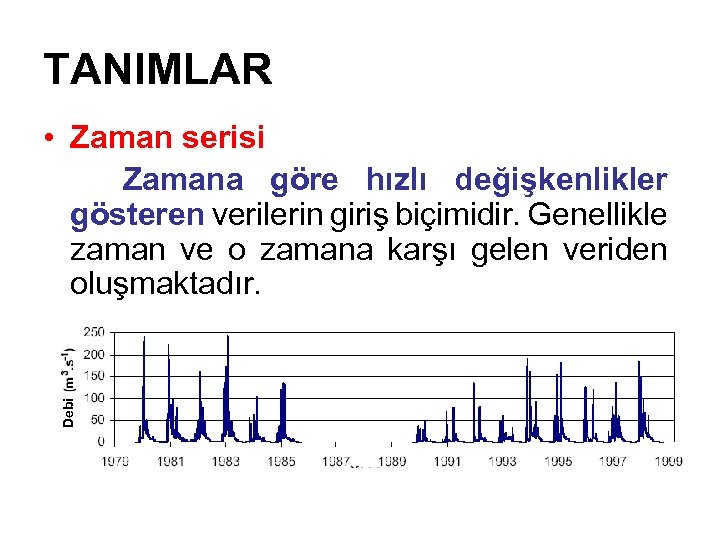TANIMLAR Debi • Zaman serisi Zamana göre hızlı değişkenlikler gösteren verilerin giriş biçimidir. Genellikle zaman ve o zamana karşı gelen veriden oluşmaktadır.

SU KALİTESİ MODELLEME YAZILIMLARI

ÇOK MODEL VAR … • 1990’lı yılların sonlarına gelindiğinde, su ekosistemi araştırmaları ve çevresel yönetim amacıyla kullanılan modellerin sayısının 4000 civarına ulaştığı tahmin edilmektedir.

MODELLEME YAZILIMLARININ BİLEŞENLERİ ve BU BİLEŞENLERİN TEMEL GÖREVLERİ • Ön işlemci (pre-processor) - Dış verilerin okunması - Model girdilerinin oluşturulması ve kontrolü • Hesap modülü - Benzetimin (simülasyonun) yapılması ve model sonuçlarının üretilmesi • Son işlemci (post-processor) - Model sonuçlarının görselleştirilmesi (zaman serisi grafikleri, animasyonlar, vb. ) ve bu sonuçların diğer analiz programları tarafından (istatistiksel analiz programları, coğrafi bilgi sistemleri, vb. ) okunabilir biçime dönüştürülmesi

MODEL GİRDİLERİ

MODEL GİRDİLERİ NEDİR ? Model girdileri, herhangi bir modelleme yazılımının çalıştırılması için gerekli verilerin tümünün, yazılıma özel bir biçimde organize edilmesiyle oluşturulan veri yapılarıdır. Model girdileri, modelleme yazılımlarının ön işlemcileri kullanılarak oluşturulurlar.

ÖN İŞLEMCİNİN BİLEŞENLERİ * • Kullanıcı arayüzü Kullanıcının verileri elle girmesini sağlar • Veri arayüzü Dış veri kaynakları (örneğin veritabanları) iletişimi sağlar. Bazı modellerin programlanabilir veri arayüzleri vardır. • Veri tutarlılığı denetçisi Girilen verilerin doğruluklarını (örneğin değer aralıklarını) ya da tutarlılıklarını denetler * Bu bileşenlerin tümü her modelleme yazılımında bulunmayabilir

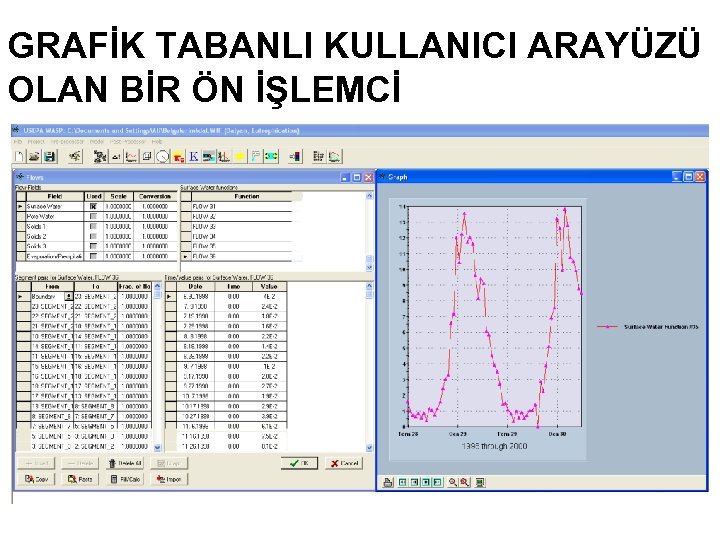GRAFİK TABANLI KULLANICI ARAYÜZÜ OLAN BİR ÖN İŞLEMCİ

VERİ ARAYÜZÜ Veri Kaynağı Veri Süzme

MODEL GİRDİLERİNİN FİZİKSEL YAPILARI… • 1960 – 1975 Her karakterin tek kodlandığı delikli kartlar • 1985 – 1990 Genellikle FORTRAN biçiminde ve yapıları delikli kart kayıtlarına benzer tek ya da az sayıda elektronik dosya • 1990’dan sonra Birçok veri kaynağına (veritabanı, coğrafi bilgi sistemi, vb. ) bağlanabilen ve proje dosyaları ile bir arada tutulan çok sayıda ve geniş kapsamlı elektronik dosya

DELİKLİ KART Şekildeki kart üzerinde yalnızca bir satırlık veri kodlanabilmekte ve orta karmaşıklıktaki bir modelin girdilerinin oluşturulabilmesi için yüzlerce kartın delme makinelerinde oluşturulup bilgisayara doğru sırada girilmesi gerekmektedir.

FORTRAN BİÇİMİNDE DOSYA NSEG NSYS ICRD MFLG IDMP NSLN INTY ZMON ZDAY 98 16 0 0 15 0 1 0. 00 0 0 1 0. 0200 0. 0000 2 1. 0000 0. 0000 1 1 1 1 0 0 1 19 1. 0000 126 51. 00 500. 00 1 2 173. 40 500. 00 50 51 58. 50 375. 00 2 3 128. 70 375. 00 51 52 75. 00 438. 00 3 5 180. 00 438. 00 52 54 819. 0000 1 1 0 ZYR HH MM 1 1. 00 1. 00 51 58 85 37 27 3 52 73 86 36 6 2 1 1 1. 00 52 73 86 36 6 2 54 74 88 26 7 1 … … … 2 0. 0250 25 1. 00 1. 00 … … … 0. 0000 0 54 74 88 26 7 1 50 56 75 39 25 5 0 0. 0250 1. 00 819. 0000 50 56 75 39 25 5 51 58 85 37 27 3 Bu dosyalar oluşturulurken çok dikkatli olunmalıdır. Hizalamada yapılan hata, verilerin yanlış okunmasına neden olabilir…

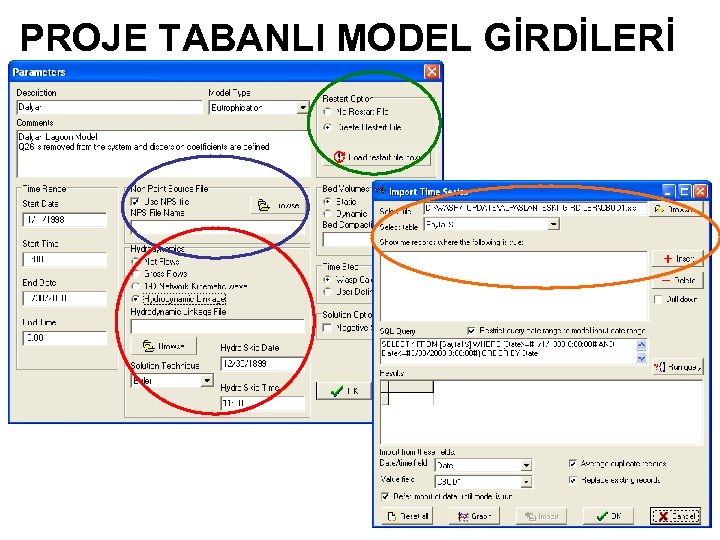PROJE TABANLI MODEL GİRDİLERİ

SU KALİTESİ MODELİ GİRDİLERİNDEKİ VERİ GRUPLARI • Benzetim (simülasyon) ile ilgili genel veriler - Dinamik modellerde benzetim zamanının başlangıcı, sonu ve zaman adımı; yatışkın durum modellerinde benzetim için temsil edici mevsim, ay ya da gün. - Modelin hangi kısımlarının (örneğin benzetime dahil edilecek su kalitesi değişkenleri) kullanılacağı ile ilgili seçenekler. - Model çıktılarının / sonuçlarının üretilmesi ile ilgili seçenekler (çıktının periyodu ve zaman aralığı) - Modelleme yazılımına özgü diğer seçenekler

SU KALİTESİ MODELİ GİRDİLERİNDEKİ VERİ GRUPLARI Basit model • Taşınım ile ilgili veriler - Öteleme (adveksiyon) ile ilgili hidrolik / hidrodinamik veriler (debi, hız, derinlik, suyun hareket yönü) - Yayılma (dispersiyon) ve çalkantı (türbülans) ile ilgili veriler (çalkantının hesaplanması ile ilgili seçenekler, yayılma katsayısı, enkesit alanları, karışım uzunluğu) - Katı madde taşınımı ile ilgili veriler (çökelme, oturma ve oyulma / yeniden askıya geçme hızları) - Sediment içindeki taşınım ile ilgili veriler (boşluk oranı, su hareketi ile ilgili veriler, yayılma ile ilgili veriler) - Canlılar yoluyla taşınım ile ilgili veriler (Lagrange taşınımı veya rasgele hareket parametreleri) Karmaşık model

SU KALİTESİ MODELİ GİRDİLERİNDEKİ VERİ GRUPLARI • Model ağı ile ilgili veriler - Kutu modellerinde kutu sayısı, kutuların hacimleri, birbirleriyle topolojik (konum, komşuluk, temas) ilişkileri; sonlu fark, sonlu eleman ve sonlu hacim modellerinde ızgara ve düğüm noktası konumları - Kutu modellerinde geometrik veriler (yüzey alanı, derinlik ya da hacim-derinlik ilişkileri; sonlu fark, sonlu eleman ve sonlu hacim modellerinde ızgara türü, koordinat sistemi, hesap elemanları ile ilgili parametreler, şekil fonksiyonları

SU KALİTESİ MODELİ GİRDİLERİNDEKİ VERİ GRUPLARI • Sınır koşulları ile ilgili veriler Bu veriler; atmosfer, kıyı çizgisi ve su ekosisteminin yatağı, modellenen su ekosistemine noktasal ve yayılı girişler ve su ekosisteminin fiziksel temasta olduğu su ekosistemlerindeki hidrodinamik ve su kalitesi değişkenlerini kapsamaktadır. Sınır koşulları, sistemi dışarıdan etkiledikleri için, itici güçler ya da zorlayıcı koşullar (forcing functions) olarak da adlandırılmaktadırlar.

SINIR KOŞULLARI İLE İLGİLİ VERİLER • Atmosfer ile ilgili veriler - Güneş ışığı şiddeti ve süresi - Bulutluluk oranı - Atmosfer koşullarını temsil eden bazı katsayılar - Hava sıcaklığı - Rüzgar hızı ve yönü

SINIR KOŞULLARI İLE İLGİLİ VERİLER • Kıyı çizgisi ve su ekosisteminin yatağı ile ilgili veriler - Kıyı çizgisinin jeomorfolojisi - Sınır tabakası kabulleri (tam sıyırma ya da sıyırmama koşulları) - Taban pürüzlülüğü

SINIR KOŞULLARI İLE İLGİLİ VERİLER • Modellenen su ekosistemine noktasal ve yayılı girişler ile ilgili veriler - Noktasal veya yayılı girişlerin debileri [L 3∙T-1] - Debi verilmeksizin girilen yükler [M∙T-1] - Noktasal veya yayılı girişlerdeki su kalitesi değişkenlerini temsil eden konsantrasyonlar [M∙L-3]

SINIR KOŞULLARI İLE İLGİLİ VERİLER • Su ekosisteminin fiziksel temasta olduğu su ekosistemlerindeki hidrodinamik ve su kalitesi değişkenleri ilgili veriler - Model ağının sınırındaki hızlar [L∙T-1], debileri [L 3∙T-1] karışım ile ilgili değişkenler - Model ağının sınırında su kalitesi değişkenlerini temsil eden konsantrasyonlar [M∙L-3]

SU KALİTESİ MODELİ GİRDİLERİNDEKİ VERİ GRUPLARI • Su ekosisteminin özellikleri ile ilgili veriler - Kinetik katsayılar ve sıcaklık düzeltme katsayıları - Stokiyometrik katsayılar - Su ortamının yapısı ile ilgili veriler

SU KALİTESİ MODELİ GİRDİLERİNDEKİ VERİ GRUPLARI • Başlangıç koşulları - Hidrodinamik değişkenlerinin konuma göre değerleri - Su kalitesi değişkenlerinin konuma göre değerleri

MODEL ÇIKTILARI

MODEL ÇIKTILARI NEDİR ? Model çıktıları, herhangi bir modelleme yazılımının çalıştırılması sırasında ya da sonrasında ürettiği verilerin ya da bilgilerin tümüdür.

MODEL ÇIKTILARININ FİZİKSEL YAPILARI… • 1960 – 1975 İlkel, tek renkli katot ışın tüpü (CRT) ekran çıktıları, iğneli çizgi yazıcı (line printer) çıktıları, metin tabanlı grafikler ve kuruma özel çıktı aygıtları • 1975 – 1990 Genellikle FORTRAN biçiminde tek ya da az sayıda elektronik dosya (Sıralı ASCII dosyaları) • 1990’dan sonra Birçok veri kaynağına (veritabanı, coğrafi bilgi sistemi, vb. ) bağlanabilen ve proje dosyaları ile bir arada tutulan çok sayıda ve geniş kapsamlı elektronik dosya, hazır grafik dosyaları, haritalar, bilimsel görselleştirme, animasyonlar

BİR ZAMANLAR MODEL ÇIKTILARI

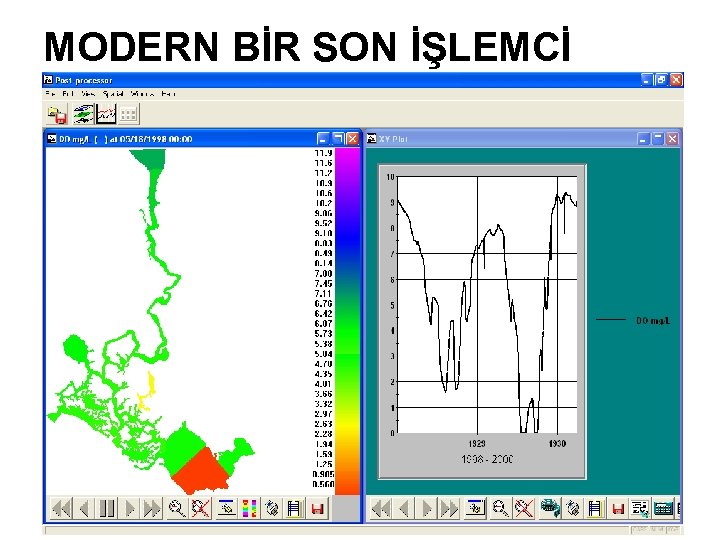MODERN BİR SON İŞLEMCİ