d3912f70b3dd44772d5fbbd2d607ccc7.ppt
- Количество слайдов: 9

Modellbasierte Software. Entwicklung eingebetteter Systeme Prof. Dr. Holger Schlingloff Institut für Informatik der Humboldt Universität und Fraunhofer Institut für offene Kommunikationssysteme FOKUS

Wieder mal ein paar Fragen? • • • Warum müssen Tools qualifiziert werden? Welche Klassen gibt es dabei? Wozu ist die ISO 9001 gut? Unterschied von ISO 9000 zu IEC 61508? Was versteht man unter einem Qualitätsmanagementsystem? Zertifizierung: Pro und Contra? Was sind “key process areas”? Verantwortung der obersten Leitung? Beispiel für Lebenszyklustätigkeiten? Beispiel für unterstützende Tätigkeiten? H. Schlingloff, SS 2014 – modellbasierte Software-Entwicklung eingebetteter Systeme Folie 2

7. Verifikation • Nachweis von (Sicherheits-) Eigenschaften § Simulation, Test § Modellprüfung § Interaktive Verifikation Idee Modellprüfung (Model Checking) • Spezifikation von Eigenschaften als temporallogische Formel § Sicherheitseigenschaft: always(nothing bad) § Lebendigkeitseigenschaft: eventually(something good) • Durchsuchen des Zustandsraumes eines Automaten oder einer Zustandsmaschine H. Schlingloff, SS 2014 – modellbasierte Software-Entwicklung eingebetteter Systeme Folie 3

Modellierung von Realzeit • Realzeitkonzepte in UML Zustandsdiagrammen § after (time) als Trigger § absoluter Zeitpunkt als Trigger • Informelle Semantik § die Transition wird t Zeiteinheiten nach dem Zeitpunkt zu dem sie aktiv wird ausgeführt § die Transition wird zur angegebenen Uhrzeit ausgeführt Zustand 1 after (5 ms) / Aktivität Zustand 2 • Vielfach nicht ausreichend § keine Mindest- / Höchstwartezeiten § keine Möglichkeit mehrere Uhren zu verwenden H. Schlingloff, SS 2014 – modellbasierte Software-Entwicklung eingebetteter Systeme Folie 4

Timed Automata • Timed Automata (zeitbeschriftete Automaten) erweitern das Konzept klassischer endlicher Automaten um (Stopp-)Uhren § Uhren laufen ständig (kein Anhalten) § alle Uhren laufen mit der selben Geschwindigkeit (perfekte Uhren, t´=1) § Uhren können durch Transitionen auf 0 zurückgesetzt werden § Uhren können das Schalten von Transitionen beeinflussen a, x: =0 S 2 S 1 x<2 x>1, b • Eine Uhr x. • Keine Invariante an s 1, also kann das System beliebig lang in s 1 bleiben. • Beim Übergang zu s 2 mit a wird die Uhr auf 0 zurückgesetzt. • In s 2 läuft die Uhr. • Frühestens 1 Zeiteinheit später ist der Übergang zu s möglich, spätestens 2 Zeiteinheiten später muss er stattfinden. H. Schlingloff, SS 2014 – modellbasierte Software-Entwicklung eingebetteter Systeme Folie 5
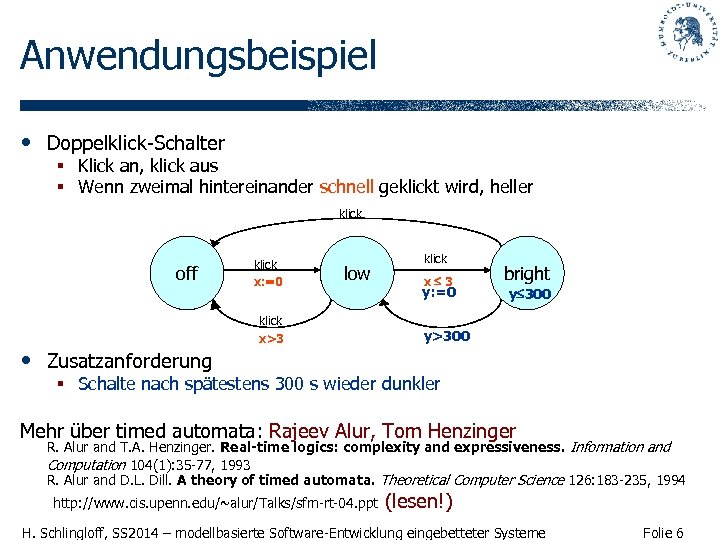
Anwendungsbeispiel • Doppelklick-Schalter § Klick an, klick aus § Wenn zweimal hintereinander schnell geklickt wird, heller klick off klick x: =0 low klick • Zusatzanforderung x>3 klick x 3 y: =0 bright y 300 y>300 § Schalte nach spätestens 300 s wieder dunkler Mehr über timed automata: Rajeev Alur, Tom Henzinger R. Alur and T. A. Henzinger. Real-time logics: complexity and expressiveness. Information and Computation 104(1): 35 -77, 1993 R. Alur and D. L. Dill. A theory of timed automata. Theoretical Computer Science 126: 183 -235, 1994 http: //www. cis. upenn. edu/~alur/Talks/sfm-rt-04. ppt (lesen!) H. Schlingloff, SS 2014 – modellbasierte Software-Entwicklung eingebetteter Systeme Folie 6

Und nun etwas formaler • Gegeben eine Menge von Zeitvariablen X. Eine zeitabhängige Bedingung ist eine boolesche Kombination von Formeln der • Art x<c, x c (rationales c) Ein zeitbeschrifteter Automat ist ein Tupel bestehend aus § § § endlicher Menge L von Orten oder Plätzen (locations) Teilmenge L 0 von Anfangsorten endliches Alphabet von Ereignissen endliche Menge von Uhren (-variablen) Invariante Inv(s) für jeden Ort (zeitabhängige Bedingung, optional) endliche Menge E von Transitionen bestehend aus - Quelle, Zielort Ereignis aus dem Alphabet (optional) zeitabhängige Bedingung (optional) Menge von Uhren die zurückgesetzt werden (optional) H. Schlingloff, SS 2014 – modellbasierte Software-Entwicklung eingebetteter Systeme Folie 7

Semantik • Jedem zeitbeschrifteten Automaten wird ein zustandsunendliches Transitionssystem zugeordnet § Zustände: (l, v) wobei l ein Ort und v eine Belegung der Uhren mit reellen Werten ist die Inv(l) erfüllt § Anfangszustände: (l 0, (0, …, 0)) § Zustandsübergänge - Kontrollschritt: (l, v) –a–>(l´, v´) falls ein Übergang (l, a, g, r, l´) - existiert mit v erfüllt g und v´=v[r: =0] Zeitschritt: (l, v) –d–>(l´, v´) falls l´=l und v´=v+d und sowohl v als auch v´ erfüllen Inv(l) • Jeder Pfad durch das Transitionssystem ist ein Ablauf des Automaten § Achtung: z. B. bei inkonsistenten Bedingungen leere Menge H. Schlingloff, SS 2014 – modellbasierte Software-Entwicklung eingebetteter Systeme Folie 8

Erweiterungen • zusätzliche Variable v 1, …, vn über endlichem Wertebereich W 1, …, Wn § Ort = (Platz, Werte (w 1, …, wn)) • Input / Output – Events § Partitionierung der Menge in Eingaben (i? ), Ausgaben (o!), und interne Ereignisse § Jede Transition darf mit einer Eingabe oder einem internen Ereignis und gleichzeitig mit mehreren Ausgaben beschriftet sein • Parallele Automaten § übliches Automatenprodukt (interleaving) Aufgabe § geben Sie eine formale Definition an § zeigen Sie dass dies keine echte Erweiterung des Modells ist H. Schlingloff, SS 2014 – modellbasierte Software-Entwicklung eingebetteter Systeme Folie 9
d3912f70b3dd44772d5fbbd2d607ccc7.ppt