Modélisation tridimensionnelle des écoulements diphasiques C Morel DER SSTH

Modélisation tridimensionnelle des écoulements diphasiques C. Morel, DER/SSTH

Plan de l’exposé • Partie I: Etablissement des équations de bilans: masse, quantité de mouvement, enthalpie totale (Eqs. primaires) • Partie II: Présentation des principales relations de fermetures • Partie III: Equations de bilans supplémentaires: exemple de l’énergie cinétique turbulente et de l’aire interfaciale volumique en écoulement à bulles. • Partie IV: Illustrations et références

PARTIE I ETABLISSEMENT DES EQUATIONS DE BILANS PRIMAIRES: • Masse • Quantité de mouvement • Enthalpie totale

Les équations locales et instantanées pour la phase k (1) • Masse: • Quantité de mouvement: • Enthalpie totale:

Les équations locales et instantanées pour la phase k (2) • Pour un fluide de Stokes et de Fourier: • Loi d’état pour chaque phase: • Qk et g sont des données du problème

Opérateur de moyenne et règles de Reynolds • Statistique (opérateur le plus général) • Temporel (écoulement stationnaire en moyenne) • Spatial (écoulement homogène en moyenne) • Linéarité de l’opérateur de moyenne • Idempotence de l’opérateur <> =

Utilisation des distributions • Traitement des discontinuités aux interfaces • Fonction Indicatrice de Phase (FIP): • Equations vérifiées par la FIP:

Extension des équations localesinstantanées au diphasique • Les dérivées de ck ne sont non nulles qu’au sens des distributions, et on a: • Exemple: bilan de masse: yk = rk

Quantité de mouvement et enthalpie • Quantité de mouvement: • Enthalpie totale Hk = hk + vk. vk/2:

Opérateur de moyenne (1) • < > = opérateur de moyenne d’ensemble • Moyenne phasique: • Taux de présence phase k: • Moyenne de Favre:

Opérateur de moyenne (2) • Moyenne aux interfaces: • Aire interfaciale volumique: • Moyenne aux interfaces pondérée par le changement de phase: • Taux de production de masse:

Equations moyennées • Masse: • Quantité de mouvement:

Décomposition du transfert de quantité de mouvement • Cas d’un écoulement à bulles:

Quantité de mouvement: forme non conservative • En soustrayant Vk*bilan masse:

Forme simplifiée dans code NEPTUNE_CFD • Hypothèse simplificatrices: pression unique: et d’où:

Bilan moyen d’enthalpie totale • Hk: enthalpie totale moyenne

Décomposition du transfert d’enthalpie totale

Enthalpie totale: forme non conservative

Forme simplifiée dans code NEPTUNE_CFD

PARTIE II PRESENTATION DES PRINCIPALES RELATIONS DE FERMETURES: • Transferts interfaciaux de masse et de chaleur • Transfert interfacial de quantité de mouvement • Transferts turbulents

Transferts interfaciaux de masse et de chaleur • Forme simplifiée du bilan interfacial d’enthalpie (Ishii, 1975; Ishii & Hibiki, 2005): • Densité de flux de chaleur:

Transferts interfaciaux de quantité de mouvement • Ecoulement à bulles (diamètre d): • Trainée: • Masse ajoutée: • Portance (lift): • Dispersion turbulente:

Transferts turbulents • Tenseur de Reynolds (e. g. phase liquide): • Viscosité turbulente: • 2 inconnues à fermer: KL et e. L

Partie III: Equations de bilans supplémentaires • Moyenne d’un scalaire passif (scalaire convecté et diffusé par l’écoulement) • Quantités turbulentes liées à l’écoulement (tensions de Reynolds, énergie cinétique turbulente…) ou au scalaire passif (variance et flux turbulent du scalaire passif) • Quantités géométriques (e. g. aire interfaciale volumique a. I, nombre volumique moyen de bulles…)

Méthodes de dérivation des équations • A partir des équations de bilans primaires (masse, quantité de mouvement, énergie) en gardant le même formalisme général (particulièrement difficile pour les grandeurs géométriques) • Pour les écoulements DISPERSES, utilisation d’un formalisme particulaire introduisant une fonction de distribution des particules fluides: en taille, en vitesse…

Exemple 1 (méthode 1): Energie Cinétique Turbulente (ECT) • Intérêt: l’ECT est une des 2 variables principales du modèle K-e permettant de fermer la viscosité turbulente. • Définition: L’ECT est la différence entre la moyenne de l’énergie cinétique du mouvement total (local et instantané) et de l’énergie cinétique du mouvement moyen:

Eq. pour l’ECT (2) • On suppose que le liquide (phase considérée) est incompressible et indilatable (r. L = cte). • La méthode de dérivation suit celle employée en monophasique, et découle directement de la définition de la grandeur (ici KL) et des propriétés de l’opérateur de moyenne.

Eq. pour l’ECT (3)

Eq. pour l’ECT (4) • • I: transport par vitesse moyenne II: diffusion turbulente III: dissipation visqueuse IV: production par le gradient de vitesse moyenne • V: production/destruction interfaciale • VI: transfert d’ECT par changement de phase

Fermeture de l’Eq. d’ECT (1) • I et IV ne nécessitent aucune modélisation supplémentaire • III sera donnée par son équation (Eq. d’e. L) • II: les 3 termes sont modélisés collectivement par une loi gradient:

Fermeture de l’Eq. d’ECT (2) • VI est généralement supposé égal à GLKL, et disparaît en mettant l’Eq. sous forme non conservative. • V: terme difficile (production ou destruction de turbulence liquide par les interfaces). Modèle simple en bulles (e. g. Lance, 1984):

Eq. d’ECT fermée

Equations de bilans géométriques • Hypothèse d’écoulement à bulles sphériques (diamètre d) • Introduction d’une fonction de distribution: f(d; x, t) telle que f(d; x, t)dd = nombre volumique de bulles de diamètre compris entre d et d + dd en (x, t) • f(d; x, t) vérifie l’équation de Liouville. Bolzmann:

Equation de Liouville-Bolzmann • Variation du diamètre (bilan masse d’une bulle):

Exemple du nombre volumique • Définition du nombre volumique de bulles: • Equation de bilan pour n: • avec les définitions:

Aire interfaciale volumique • Définition de l’aire interfaciale volumique: • Equation de bilan pour a. I: • avec les définitions:

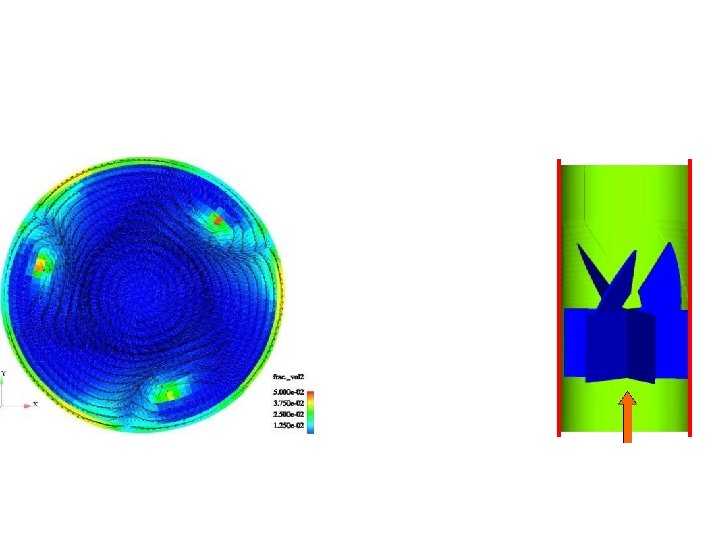
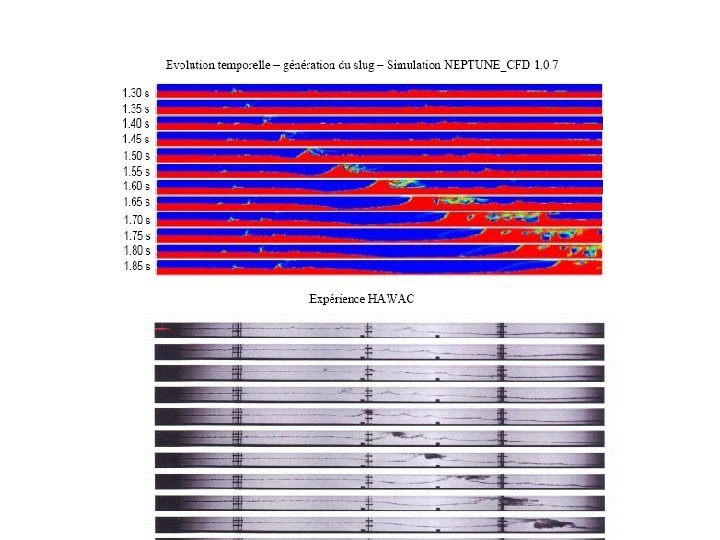
Sur les équations du modèle à deux fluides • • Ishii M. , 1975, Thermo-fluid dynamic theory of two-phase flow, Eyrolles, Paris. Ishii M. , Hibiki T. , 2006, Thermo-fluid dynamics of two-phase flow, Ed. Springer. Oesterlé B. , 2006, Ecoulements multiphasiques, Ed. Hermès, Lavoisier. Drew D. A. , Passman S. L. , 1999, Theory of Multicomponent Fluids, Applied mathematical sciences 135, Ed. Springer. Ishii M. , 1990, Two-fluid model for two-phase flow. Multiphase Science and Technology, Hewitt G. F. , Delhaye J. M. , Zuber N. Eds. , Vol. 5, pp. 1 -58. Kataoka I. , 1986, Local instant formulation of two-phase flow, Int. J. Multiphase Flow, Vol. 12, No. 5, pp. 745 -758. Kolev, N. I. , 2002 a, Multiphase Flow Dynamics 1: Fundamentals, Ed. Springer. Nigmatulin R. I. , 1991, Dynamics of multiphase media, Vol. 1, Hemisphere Publishing Corporation, New-York, Washington, Philadelphia, London.

Sur la turbulence diphasique • • Kataoka I. , Serizawa A. , 1989, Basic equations of turbulence in gas-liquid two-phase flow, Int. J. Multiphase Flow Vol. 15, No. 5, pp. 843 -855. Lance M. , Bataille J. , 1991, Turbulence in the liquid phase of a uniform bubbly air/water flow, J. Fluid Mech. , Vol. 222, pp. 95 -118. Lance M. , Marié J. L. , Bataille J. , 1984, Modélisation de la turbulence de la phase liquide dans un écoulement à bulles, La Houille Blanche, No. ¾. Lance M. , Marié J. L. , Bataille J. , 1991, Homogeneous turbulence in bubbly flows, J. Fluids Engineering, Vol. 113, pp. 295 -300. Lance M. & Lopez de Bertodano M. , 1994, Phase distribution phenomena and wall effects in bubbly two-phase flows, Multiphase Science and Technology, Vol. 8, Hewitt G. F. , Kim J. H. , Lahey R. T. Jr. , Delhaye J. M. & Zuber N. , Eds, Begell House, pp. 69 -123. Lopez de Bertodano M. , Lahey R. T. , Jones O. C. , 1994, Phase distribution in bubbly twophase flow in vertical ducts, Int. J. Multiphase Flow Vol. 20, No 5, pp 805 -818. Lopez de Bertodano M. , Lahey R. T. Jr. , Jones O. C. , 1994, Development of a K-e model for bubbly two-phase flow, Transactions of the ASME, J. of Fluids Eng. , Vol. 116, pp. 128 -134. Morel C. , 1995, An order of magnitude analysis of the two-phase K-e model, Int. J. Fluid Mech. Research, Vol. 22, Nos. 3&4, pp. 21 -44.

Sur l’aire interfaciale volumique • • • Lhuillier D. , Morel C. , Delhaye J. M. , 2000, Bilan d’aire interfaciale dans un mélange diphasique: approche locale vs approche particulaire, C. R. Acad. Sci. Paris, t. 328, Série IIb, pp. 143 -149. Morel C. , Goreaud N. , Delhaye J. M. , 1999, The local volumetric interfacial area transport equation: derivation and physical significance, Int. J. Multiphase Flow 25, pp. 1099 -1128. Yao W. , Morel C. , 2004, Volumetric interfacial area prediction in upward bubbly two-phase flow, Int. J. Heat Mass Transfer 47 (2), pp. 307 -328. Morel C. , 2007, On the surface equations in two-phase flows and reacting single-phase flows, International Journal of Multiphase Flow 33, pp. 1045– 1073 Delhaye J. M. , 2001, Some issues related to the modeling of interfacial areas in gas-liquid flows, Part I: The conceptual issues, C. R. Acad. Sci. Paris, t. 329, Série II b, pp. 397 -410. Delhaye J. M. , 2001, Some issues related to the modeling of interfacial areas in gas-liquid flows, Part II : Modeling the source terms for dispersed flows, C. R. Acad. Sci. Paris, t. 329, Série II b, pp. 473 -486.