Моделирование.ppt
- Количество слайдов: 105

МОДЕЛИРОВАНИЕ ХИМИКОТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ПЕРЕРАБОТКИ ПОЛИМЕРОВ

МЫ ИЗУЧАЕМ МОДЕЛИ, А НЕ ГРЯЗНУЮ ДЕЙСТВИТЕЛЬНОСТЬ

Структура курса n 1. Основные понятия. n 2. Физико-химические основы моделирования. n 3. Элементы теории эксперимента. n 4. Принципы оптимизации химикотехнологических процессов. n 5. Моделирование основных химикотехнологических процессов переработки полимеров.

1. Основные понятия n 1. 1. Модели и моделирование n Моделирование: создание модели, ее исследование и распространение полученных результатов на оригинал. n Модель: некая система, которая ставится в соответствие оригиналу для его описания.

Закон и модель Свойства законов и моделей. Гипотезы. Y=a+b. X
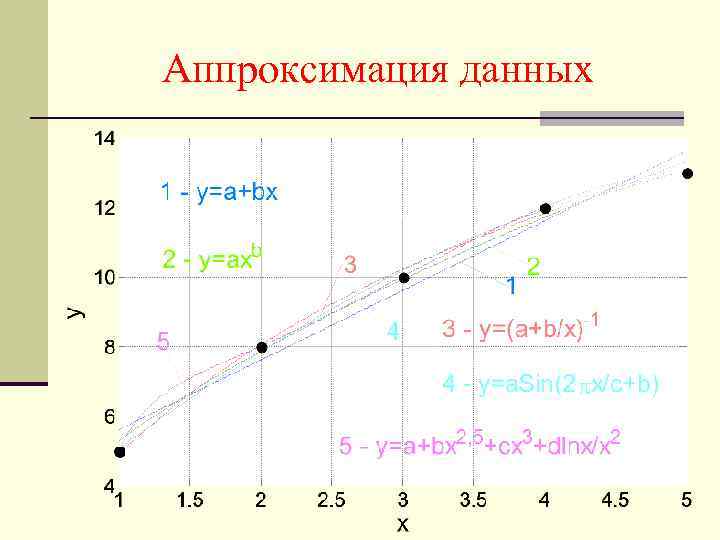
Аппроксимация данных

Свойства диффузных систем n 1) нет непроницаемых перегородок между различными физико-химическими процессами, которыми сопровождается функционирование таких систем; n 2) высокая размерность задачи; n 3) связи между переменными не носят функционального характера; n 4) для описания диффузных систем используются методы многофакторного эксперимента.

Методы описания ПОС n. Многомерная математическая статистика. Р. Фишер. n. Кибернетический подход. Н. Винер.

1. 2. Полимер как объект исследования n — Высокая молекулярная масса. n — Полидисперсность – смесь гомологов. n — Многокомпонентность, многофазность, гетерогенность, анизотропия. n — Неконтролируемые переменные. n — Низкая точность. n — Инерционность. n — Противоречивые требования. n — Инерция мышления.

1. 3. Классификация моделей n 1. Математические (эскизные, программные, комбинированные, локально-интегральные). n 2. Физические. n 3. Схематические. n Требования к процессу моделирования: экономичность, традуктивность. n Факторы и отклики. n Критерии качества модели: адекватность, содержательность, предсказательная способность.

1. 4. Способы моделирования n 1. 4. 1. Теория подобия. n. Три уравнения сохранения массы, энергии и импульса. n Локальное изменение + конвективное изменение + диффузионное изменение + изменение за счет производства = 0

Уравнение сохранения массы n с – концентрация, t – время, v – скорость, х – линейная координата, D – коэффициент диффузии, r – скорость реакции на единицу объема, r=kc, r=kc 2 и т. д. , km – коэффициент массопереноса, а – поверхность на единицу объема.

Уравнение сохранения энергии n Cp – теплоемкость, – плотность, Т – температура, – теплопроводность, q – скорость образования тепла на единицу объема, – коэффициент теплоотдачи.

Уравнение сохранения момента n – динамическая вязкость, f – сила на единицу объема, – напряжение сдвига, – поверхностное натяжение, l – длина на единицу объема.
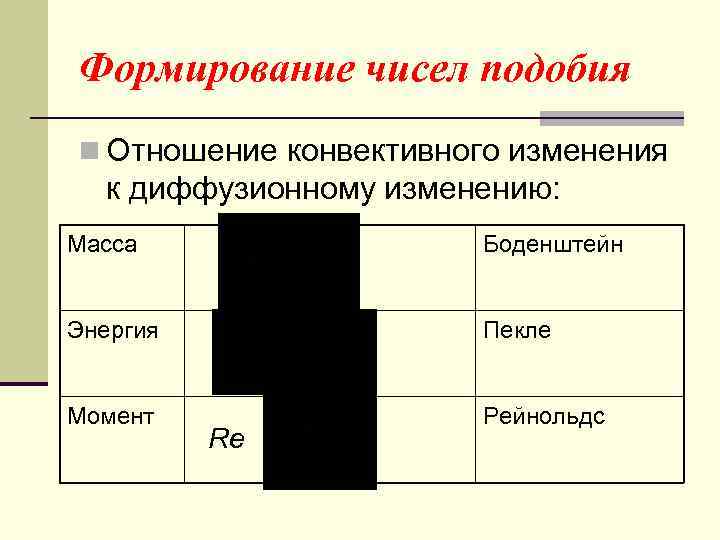
Формирование чисел подобия n Отношение конвективного изменения к диффузионному изменению: Масса Боденштейн Энергия Пекле Момент Рейнольдс Re
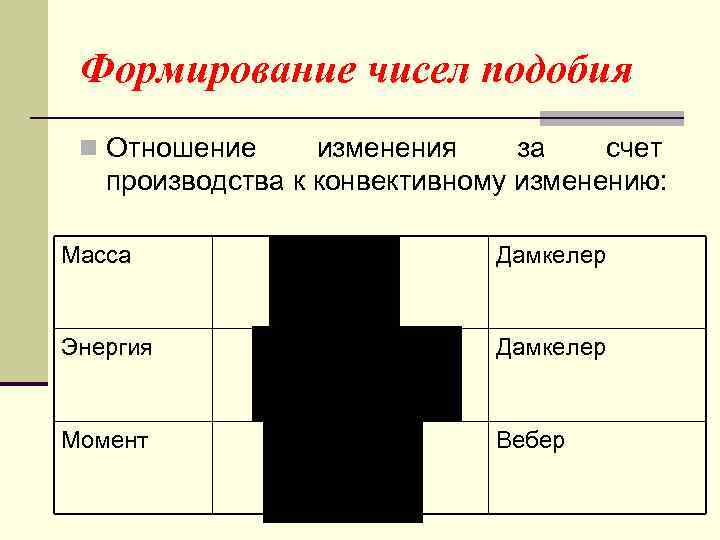
Формирование чисел подобия n Отношение изменения за счет производства к конвективному изменению: Масса Дамкелер Энергия Дамкелер Момент Вебер

Формирование чисел подобия n Отношение соотношения для граничных условий к конвективному изменению: Масса Меркель Энергия Стентен Момент Фанниган
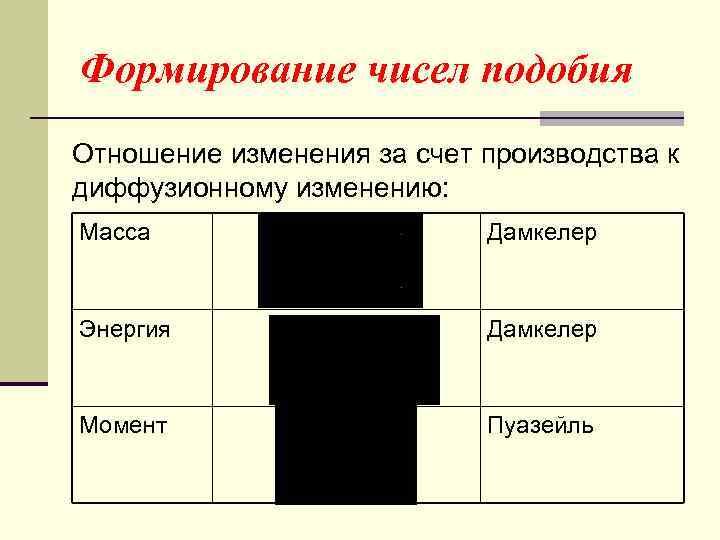
Формирование чисел подобия Отношение изменения за счет производства к диффузионному изменению: Масса Дамкелер Энергия Дамкелер Момент Пуазейль

Формирование чисел подобия Отношение соотношения для граничных условий к диффузионному изменению: Масса Шервуд Энергия Нуссельт Момент Бингам
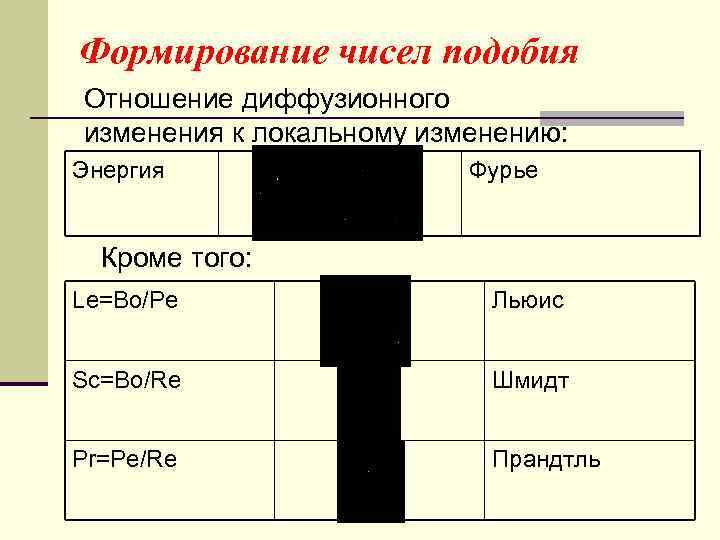
Формирование чисел подобия Отношение диффузионного изменения к локальному изменению: Энергия Фурье Кроме того: Le=Bo/Pe Льюис Sc=Bo/Re Шмидт Pr=Pe/Re Прандтль

Критерий контакта n Ko=kn. Zn– 1 t n Z – изменение суммарного теплового эффекта qсум, изменение крутящего момента М, изменение количества узлов сетки , изменение концентрации прореагировавшего реагента с.
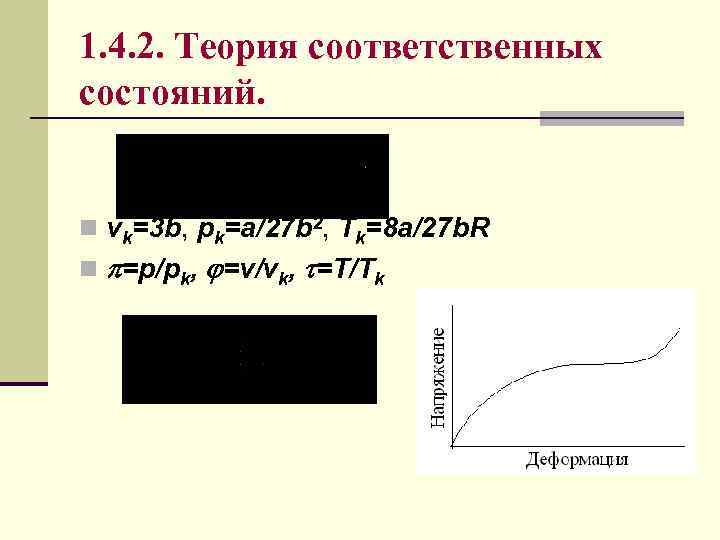
1. 4. 2. Теория соответственных состояний. n vk=3 b, pk=a/27 b 2, Тk=8 a/27 b. R n =p/pk, =v/vk, =T/Tk

1. 4. 3. Метод аналогий. Уравнение Дарси-Вейсбаха, w – скорость фильтрации, gradp – градиент давления, k – коэффициент фильтрации. Уравнение Ньютона, – напряжение сдвига, gradw – градиент скорости, – динамическая вязкость. Закон Био-Фурье, q – тепловой поток, grad. T – градиент температуры, – теплопроводность. Первый закон Фика, m – поток массы, gradc – градиент концентрации, D – коэффициент диффузии. Закон Ома, i – сила тока, gradu – градиент напряжения, – электрическая проводимость.

Дифференциальные уравнения n Обобщенные заряд и потенциал Второй закон Фика, уравнение диффузии. Дифференциальное уравнение теплопроводности Фурье. Уравнение Навье-Стокса, основное реологическое соотношение. Телеграфное уравнение цепи емкостей и сопротивлений.
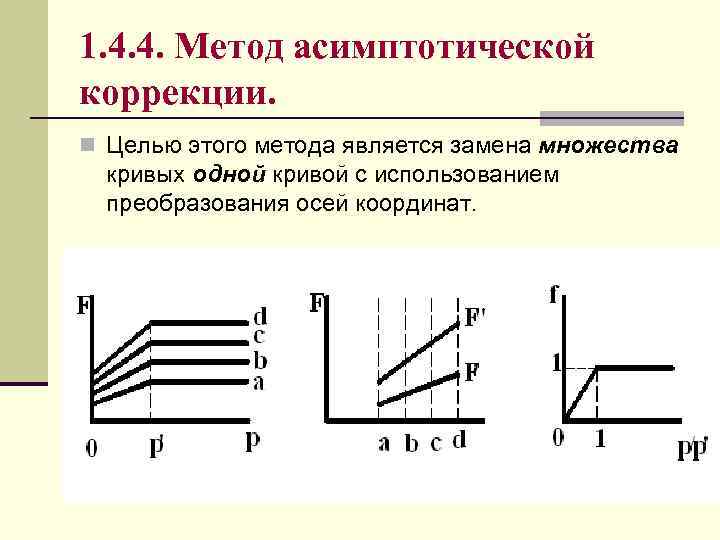
1. 4. 4. Метод асимптотической коррекции. n Целью этого метода является замена множества кривых одной кривой с использованием преобразования осей координат.

1. 5. Этапы моделирования. n — Получить математическое описание оригинала n n n – идентификация объекта моделирования. — Выбор или создание алгоритма моделирования – как вести математическую обработку данных. — Написание программы для ЭВМ. — Машина выдает результат математического моделирования – решение задачи. — Проверка адекватности модели. Если модель неадекватна, то производится ее коррекция и получается новое решение. — Интерпретация полученных результатов и принятие решений.

1. 6. Химико-технологический процесс как система. n — Система представляет собой множество подсистем и/или элементов с их связями и отношениями, формирующими некоторое целостное образование. n — Компоненты системы: вход, выход, ограничения и связи. n — Связи бывают аддитивными, синергическими и антагонистическими.

Направленность связей. n * Связи взаимодействия свойств (например, n n n физические формулы) и объектов (например, молекулярные связи). * Связи порождения, когда один объект вызывает к жизни другой (например, химические реакции). * Связи преобразования (например, явление катализа). * Связи строения (например, химические связи). * Связи функционирования (например, связи, обеспечивающие работу машины, агрегата). * Связи развития – не просто смена состояний, но совокупность элементов, проникнутая как бы "стержневой" идеей. * Связи управления, строящиеся на основе определенных программ

Системные характеристики. Гомогенность – система состоит из однородных элементов. Элементарность – ни один элемент системы нельзя рассматривать как подсистему. Минимальность – система уничтожается при уничтожении хотя бы одного элемента. Незавершенность – система допускает присоединение новых элементов без превращения в другую систему. Завершенные системы – наоборот. Упорядоченность – существенен порядок расположения элементов в системе. Имманентность – системообразующие отношения справедливы только для этой системы. Элементарноавтономность – элемент системы обладает всеми свойствами системы. — Минимальная система не является элементарноавтономной; если система элементарноавтономная, она незавершенная; если система минимальная и незавершенная, она не элементарноавтономная. — Иерархическая структура системы: молекулярный уровень; уровень малого объема; уровень рабочей зоны аппарата; уровень аппарата; уровень агрегата.

2. Физико-химические основы моделирования n 2. 1. Теплообмен. n 2. 1. 1. Виды теплообмена. n. Теплопроводность n. Конвекция n. Излучение

2. 1. 2. Уравнение теплового баланса. n Конструкторский тепловой расчет n Поверочный тепловой расчет n Энергосберегающие технологии nе Q+=е Q 2. 1. 3. Способы обогрева
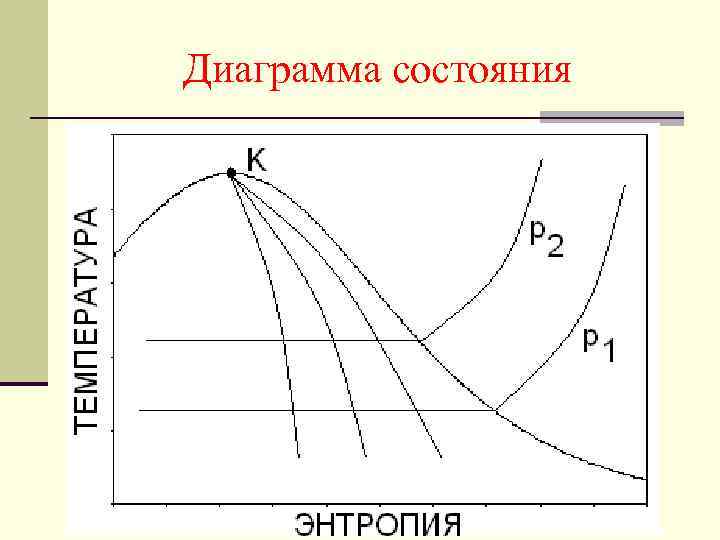
Диаграмма состояния
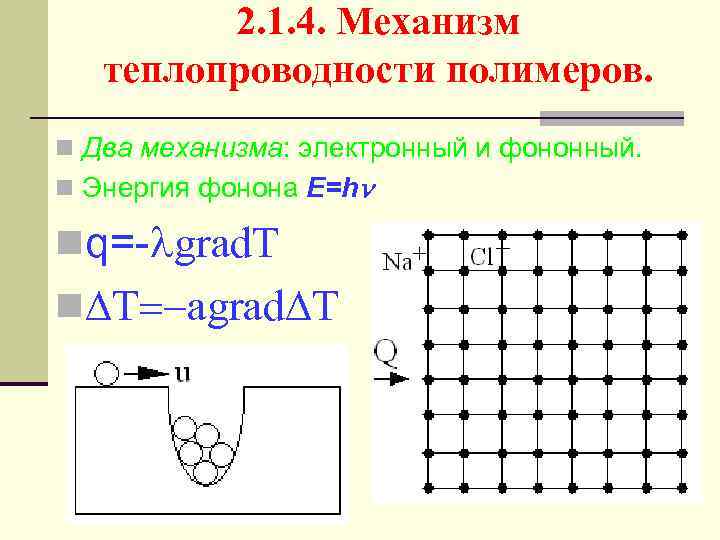
2. 1. 4. Механизм теплопроводности полимеров. n Два механизма: электронный и фононный. n Энергия фонона E=h nq=- grad. T n T=-agrad T

Скорость звука и поглощение n При М’>>M” n M’=u 2 ; ’=2 M’r/ ; r= u/ n qсум= qvdt n Уравнение Дебая-Киттеля =Au. C l
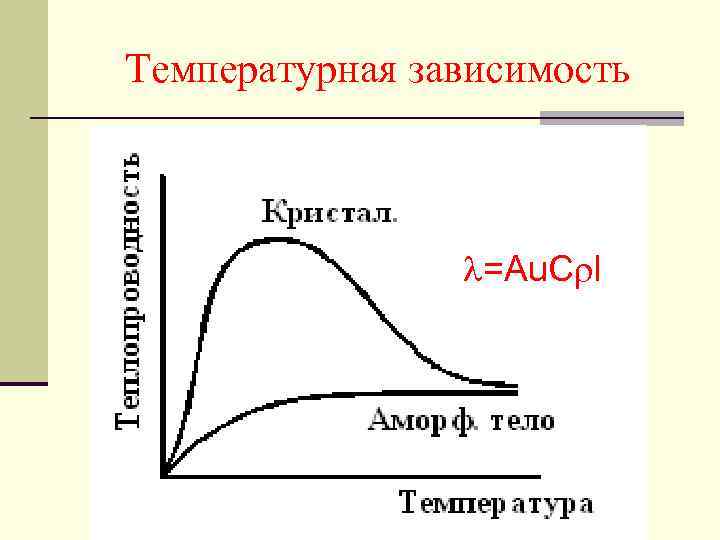
Температурная зависимость =Au. C l
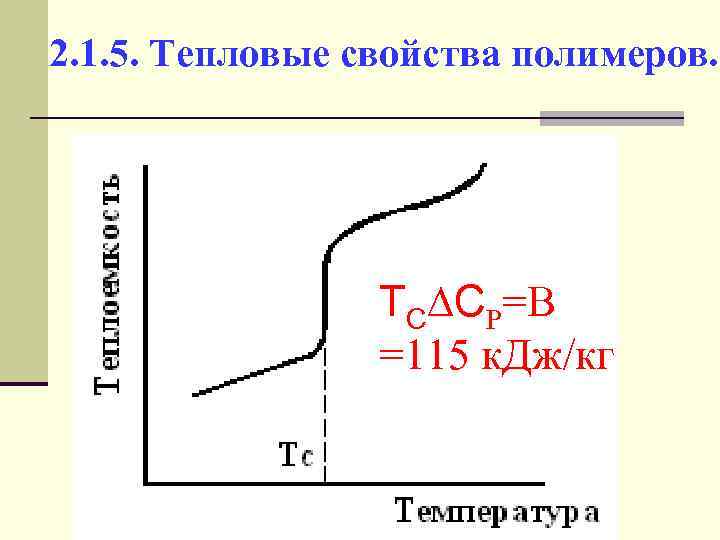
2. 1. 5. Тепловые свойства полимеров. TC CP=B =115 к. Дж/кг
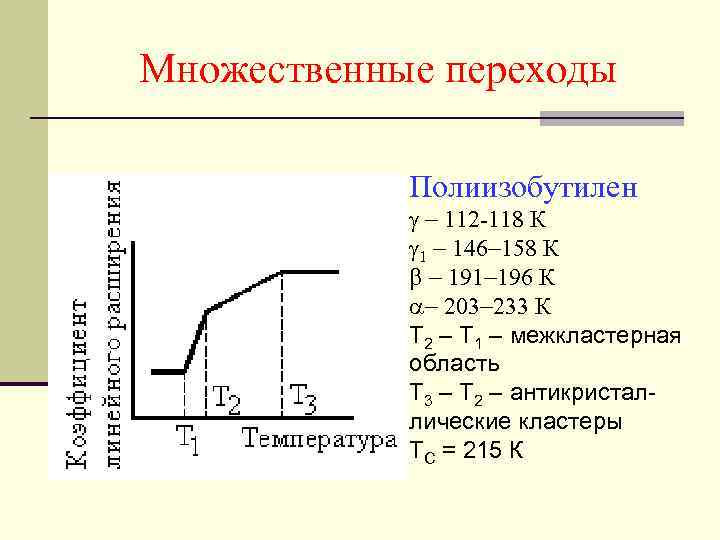
Множественные переходы Полиизобутилен - 112 -118 К 1 - 146 -158 К b - 191 -196 К - 203 -233 К T 2 – T 1 – межкластерная область T 3 – T 2 – антикристаллические кластеры ТС = 215 К
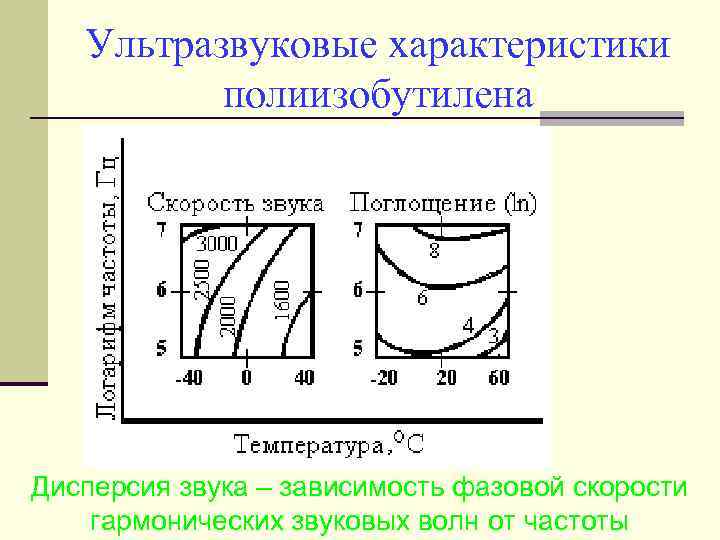
Ультразвуковые характеристики полиизобутилена Дисперсия звука – зависимость фазовой скорости гармонических звуковых волн от частоты
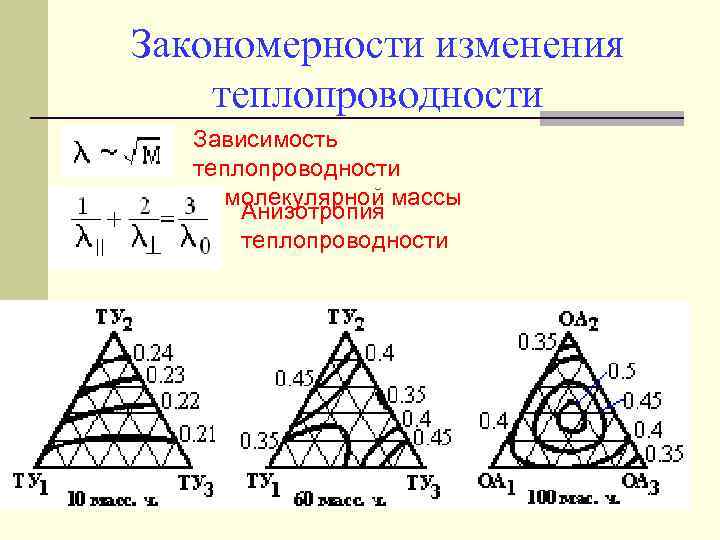
Закономерности изменения теплопроводности Зависимость теплопроводности от молекулярной массы Анизотропия теплопроводности

2. 1. 6. Дифференциальное уравнение теплопроводности Аналитические методы – Разделение переменных и интегральные преобразования. Условия однозначности: физические, начальные (временные), граничные Численные методы (МКР, МКЭ) Методы аналогий

Решение дифференциального уравнения теплопроводности Условия однозначности: 1) геометрические условия – бесконечная пластина; 2) физические условия – теплофизические характеристики материала известны и принимаются неизменными при нагреве и охлаждении; внутренними источниками и стоками тепла пренебрегаем; 3) начальные условия – в момент времени t=0 во всех точках пластины температура Т 0 одинакова; 4) граничные условия – третьего рода; коэффициент теплоотдачи на обеих поверхностях пластины одинаков и не зависит от времени, постоянна также и температура окружающей среды Тс.

Решение дифференциального уравнения теплопроводности

Решение дифференциального уравнения теплопроводности ;
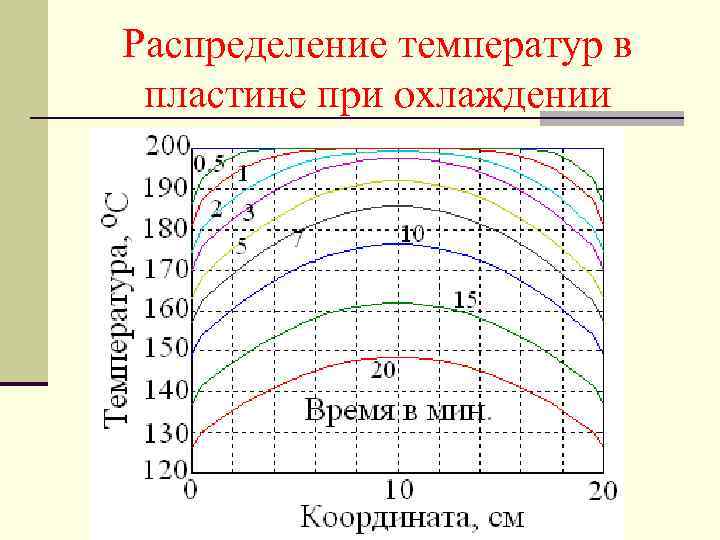
Распределение температур в пластине при охлаждении

2. 1. 7. Использование расчетных методов для ориентировочной оценки свойств полимеров. u – скорость продольной волны; U – функция Рао мономерного звена; V – молярный объем мономерного звена; – коэффициент Пуассона; а – температуропроводность; l – длина свободного пробега фонона (принимается 6 10 -11 м). Для полимеров в стеклообразном состоянии составляет 0. 33, для кристаллического состояния – 0. 40 и, наконец, в случае каучуков – 0. 49. тогда поправка составляет 0. 994, и можно пользоваться третьей упрощенной формулой.

2. 2. Реология. n 2. 2. 1. Предмет реологии. n Реология – наука о течении и деформации реальных сплошных сред. Она рассматривает процессы, связанные с необратимыми остаточными деформациями вещества, и является областью науки, находящейся между гидродинамикой и теорией упругости. Обычные уравнения гидродинамики вязкой жидкости неприменимы для реологических тел, т. к. эти тела обладают аномалией вязкости. Если, например, для дисперсных систем применять закон течения Ньютона, вязкость их оказывается непостоянной, а меняется (уменьшается) с увеличением скорости течения.

2. 2. 2. Классификация жидкостей Ньютоновская жидкость d. L = vdt – перемещение плоскости d =d. L/r=vdt/r –деформация d /dt=dv/dr

Кривые течения 1 – Тело Бингама. 2 – Ньютоновская жидкость =tg. 3 – Тело Сен-Венана. 4 – Дилатантная жидкость. 5 – Псевдопластичное тело.

Тело Бингама Предел текучести – отрезок на оси ординат. Вязкие полимеры – течение начинается при любом напряжении сдвига. Пластичные полимеры – имеют предельное напряжение сдвига, ниже которого течение не возникает. Тело Бингама – упругое твердое тело ниже предела текучести и жидкость, когда напряжение сдвига больше этого предела Т. При <Т = ; при >Т Это эмпирическое уравнение описывает реологическое поведение латексов типа полимерных эмульсий, используемых в красках, паст и суспензий (кетчуп).

Дилатантные системы характерны для суспензий с большим содержанием твердых частиц. При малых скоростях сдвига близки к ньютоновским жидкостям. Тело Сен-Венана может быть представлено элементом, лежащим на плоскости и не обладающим инерцией. Тело не начинает двигаться, пока напряжение не станет больше предельного. После этого может двигаться с любой скоростью. Псевдопластичное тело. Обычно с ростом напряжения сдвига скорость течения растет быстрее, чем это следует из законы Ньютона. Ускорение течения обусловлено падением вязкости из-за изменения структуры полимера. Падение вязкости с ростом напряжения сдвига называется аномалией вязкости, а вязкость называется эффективной.
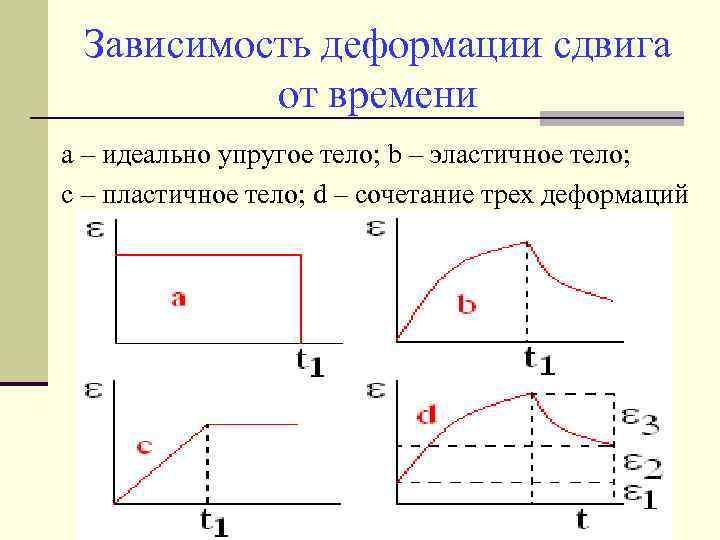
Зависимость деформации сдвига от времени a – идеально упругое тело; b – эластичное тело; с – пластичное тело; d – сочетание трех деформаций
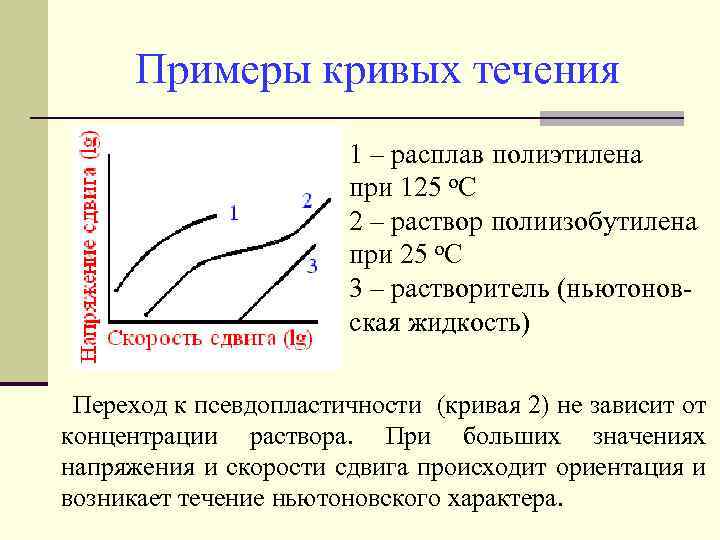
Примеры кривых течения 1 – расплав полиэтилена при 125 о. С 2 – раствор полиизобутилена при 25 о. С 3 – растворитель (ньютоновская жидкость) Переход к псевдопластичности (кривая 2) не зависит от концентрации раствора. При больших значениях напряжения и скорости сдвига происходит ориентация и возникает течение ньютоновского характера.

2. 2. 3. Законы течения неньютоновских жидкостей Деформация идеального упругого тела – закон Гука Деформация идеального вязкого тела – закон Ньютона Формула Бингама: = *+ к/ = *+ к */( - к) = * /( - к) * – пластическая вязкость к – предел текучести

Уравнение Эйринга-Паулла , B, AEP – эмпирические константы. при низких скоростях сдвига ньютоновское течение (формула Бингама). при высоких скоростях сдвига также ньютоновское течение (формула Ньютона). Недостаток уравнения – экспериментально не подтверждается

Уравнение Оствальда-Вейла n – индекс течения, 1/n =1 -5; K – коэффициент консистенции; K 0 – K при Т=Т 0; Е – энергия активации вязкого течения;
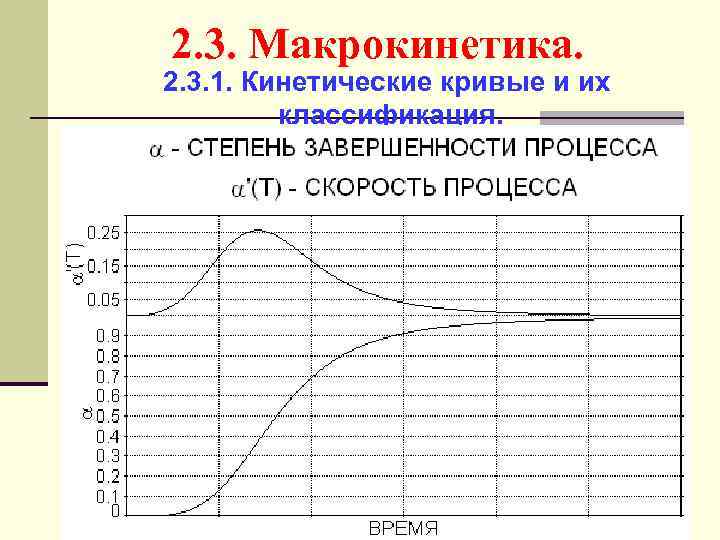
2. 3. Макрокинетика. 2. 3. 1. Кинетические кривые и их классификация.

2. 3. 2. ОПРЕДЕЛЕНЕ КИНЕТИЧЕСКИХ ПАРАМЕТРОВ ПРОЦЕССА k 1 и k 2 – константы скорости; n - порядок реакции; [0. 5; 0. 9].

2. 3. 3. Классификация функций распределения I k<0 II k=0 III k=

Кривые Пирсона IV V k=1 VI VII k=0

3. Элементы теории эксперимента. 3. 1. Основные концепции теории эксперимента. ¾ Природа статистических выводов. ¾ Рандомизация. ¾ Иерархия моделей. ¾ Критерии оптимальности. ¾ Редукция. ¾ Концепция случая.

3. 2. Статистические оценки и проверка статистических гипотез. ¾ Генеральная совокупность и выборка. ¾ Состоятельность и несмещенность. ¾ Среднее значение. ¾ Характеристики разброса. Дисперсия и коэффициент вариации. ¾ Доверительные интервалы.

Проверка гипотез ¾ Необходимое количество наблюдений. ¾ Исключение грубых промахов. ¾ Проверка однородности дисперсий. ¾ Сравнение средних значений. ¾ Значимость коэффициентов. ¾ Адекватность модели. ¾ Содержательность модели. ¾ Предсказательная способность.

3. 3. Планирование эксперимента. Область математической статистики, ставящая своей целью выбор количества и условий постановки экспериментов, необходимых и достаточных для решения задачи с требуемой точностью, разработку методов и приемов математической обработки результатов эксперимента и принятия на основе этого определенных решений.

3. 3. 1. Линейные планы - Классификация. - Пассивный и активный эксперимент. - Полный факторный эксперимент. - Дробные реплики. ПФЭ 22 Y=b 0+b 1 X 1+b 2 X 2+b 12 X 1 X 2 Xj=(Zj–Zj 0)/Az, – 1 Xj +1 Az = (Zjmax–Zjmin)/2

Линейные планы ПФЭ 23 Y=b 0+b 1 X 1+b 2 X 2+b 3 X 3+ +b 12 X 1 X 2+b 13 X 1 X 3+ +b 23 X 2 X 3+b 123 X 1 X 2 X 3 ОК: X 3=X 1 X 2 b 1 1 + 2 3 ДФЭ 23 -1 ГС: 1=X 1 X 2 X 3 b 3 3 + 1 2 b 2 2 + 1 3 b 0 0 + 1 2 3
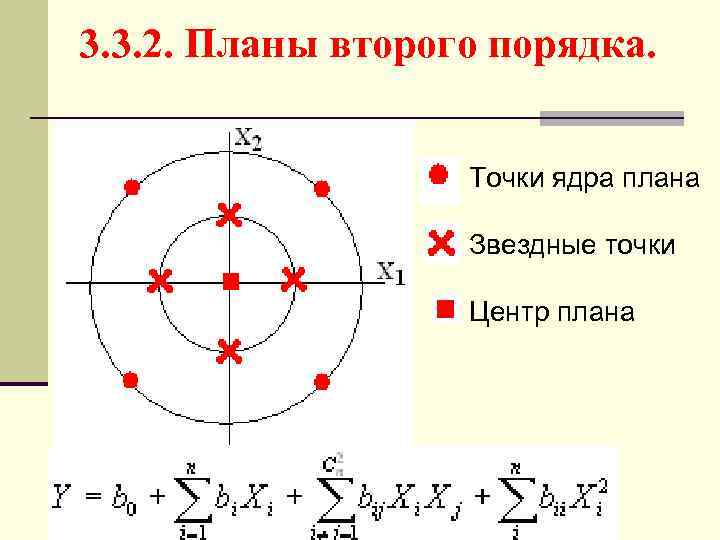
3. 3. 2. Планы второго порядка. Точки ядра плана Звездные точки Центр плана
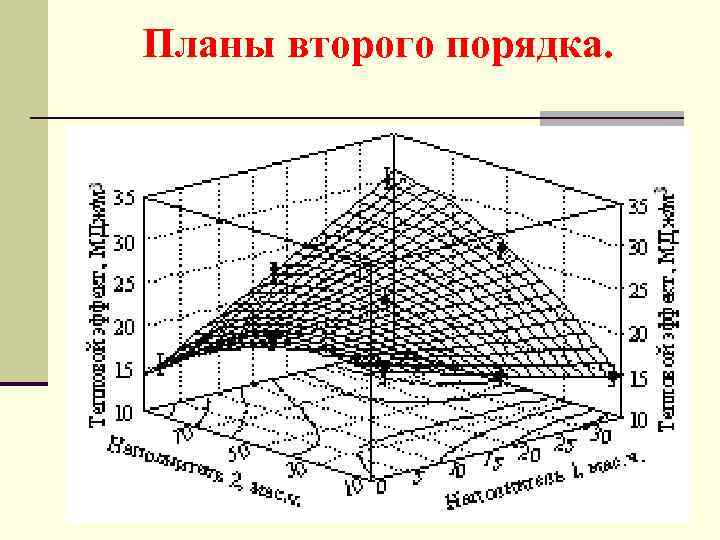
Планы второго порядка.

4. Оптимизация химикотехнологических процессов. 4. 1. Одномерный поиск. — Метод последовательной дихотомии — Метод золотого сечения m/(n – m) = (n – m)/n m 0. 382 n 4. 2. Многомерный поиск. — Метод крутого восхождения — Метод покоординатного поиска — Последовательный симплексный метод 4. 3. Промышленный эксперимент.
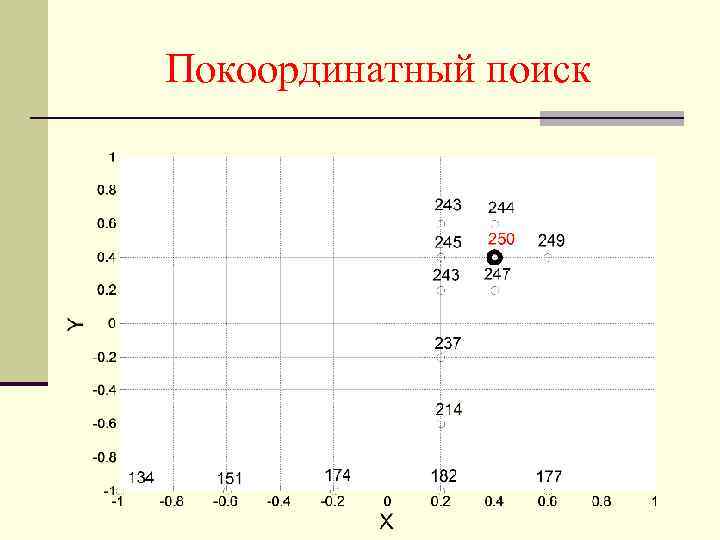
Покоординатный поиск
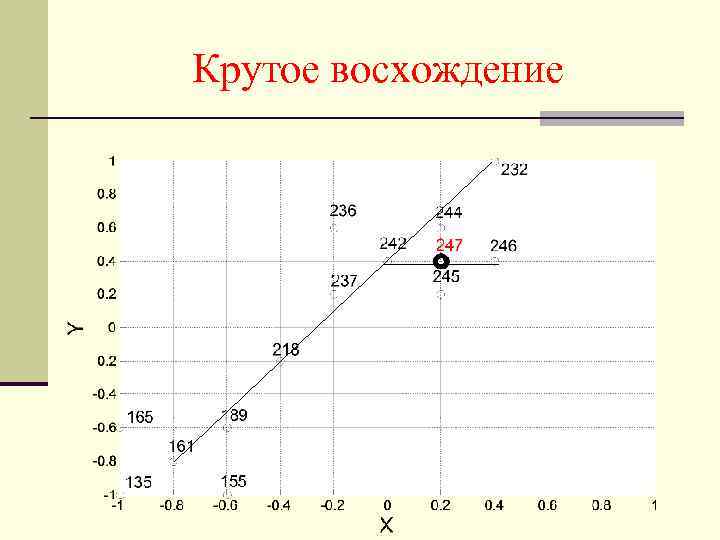
Крутое восхождение
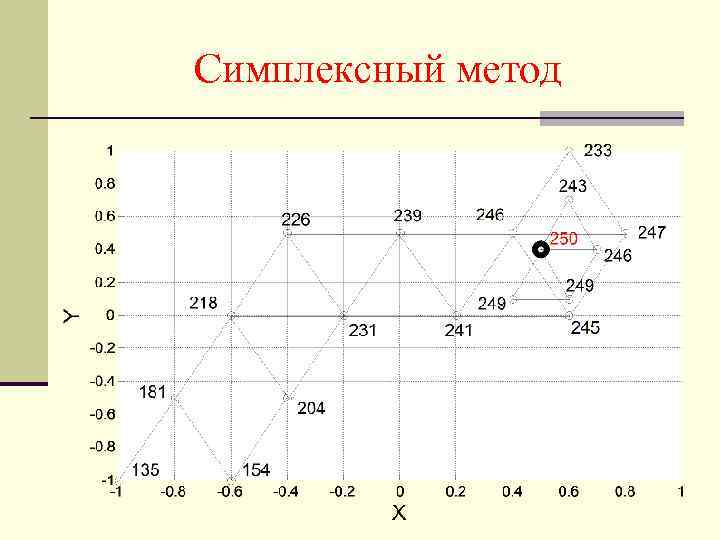
Симплексный метод

5. Моделирование процессов переработки полимеров. 5. 1. Смешение. 5. 1. 1. Общие сведения. Необходимость процесса. Основное требование – однородность свойств. Переход: порядок – беспорядок. Диффузия затруднена: необходимость приложения внешних сил. - Течение ламинарное – малое значение числа Рейнольдса. - Простое и диспергирующее смешение. -
Смешение Машинные параметры: скорость, геометрия, зазоры, температурный режим. Условия процесса: напряжение сдвига, скорость сдвига, температура, время. Свойства материала: дисперсность, гомогенность, текучесть, набухание, механические характеристики.
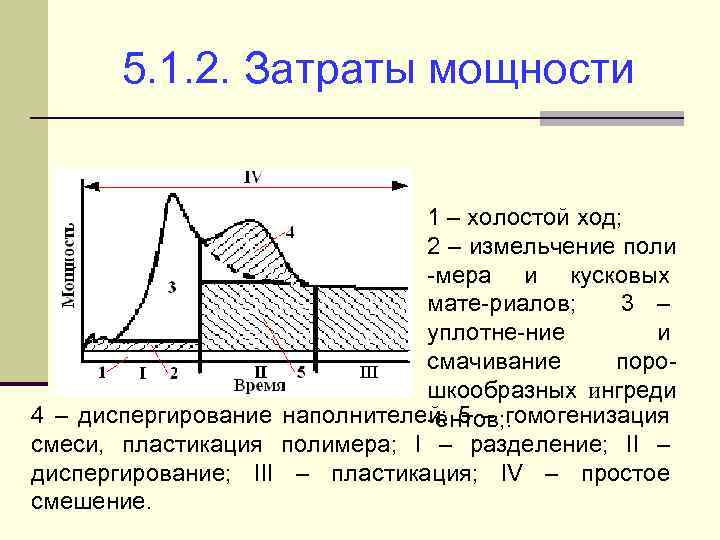
5. 1. 2. Затраты мощности 1 – холостой ход; 2 – измельчение поли -мера и кусковых мате-риалов; 3 – уплотне-ние и смачивание порошкообразных ингреди 4 – диспергирование наполнителей; 5 – гомогенизация -ентов; . смеси, пластикация полимера; I – разделение; II – диспергирование; III – пластикация; IV – простое смешение.

5. 1. 3. Механизм ламинарного смешения n Основные явления: изменение агрегатного состояния; молекулярной массы; набухание; деструкция; структурирование. n Изменение поверхности раздела фаз. 1. Диспергирование: V= D 3/6; S= D 2; V=n d 3/6; d=D/n 1/3; S'=n d 2; d 2=D 2/n 2/3; S'=Sn 1/3>S. 2. Растяжение: куб V=a a a; параллелепипед V=a 1 b; a 1=a/k; S=6 а 2; S'=2 a 2/k 2+4 a 2/k > S. 3. Сдвиг:

5. 1. 4. Схема процесса = 1 А= 2 Б= 1 В; А=(VA–VБ)/h; В=VВ/h; Б=(VБ–VВ)/(H– 2 h); VA–VБ=VВ; VБ=VA–VВ; Б=(VА– 2 VВ)/(H– 2 h); Б=(VА– 2 Вh)/(H– 2 h); В= Б 2/ 1; Б=(VА– 2 Бh 2/ 1)/(H– 2 h); Б=VА/(H– 2 h) – 2 Бh 2/ 1/(H– 2 h); Б(1+2 h 2/ 1/(H– 2 h))=VА/(H– 2 h); Б=VА/(H– 2 h+2 h 2/ 1) Целесообразно добавлять менее вязкий компонент к более вязкому, т. е. понижать отношение 2/ 1 и повышать скорость сдвига

5. 1. 5. Смешение на вальцах. n Допущения: n 1. Режим течения между валками– ламинарный. n 2. Материал прилипает к поверхностям валков. n 3. Гравитационные и инерционные силы малы по сравнению с силами поверхностными. n 4. Течение материала одномерное, т. е. материал перемещается в основном в зазор vz=0; vy «vx и vx/ y « vy/ y. n 5. Гидромеханические давления на входе полимера в валки и выходе из них равны нулю. p/ y= p/ z=0.

Уравнение Навье-Стокса Уравнение отличается от уравнений вязкой ньютоновской жидкости тем, что в это уравнение вместо коэффициента вязкости ньютоновской жидкости входит коэффициент эффективной вязкости эф.
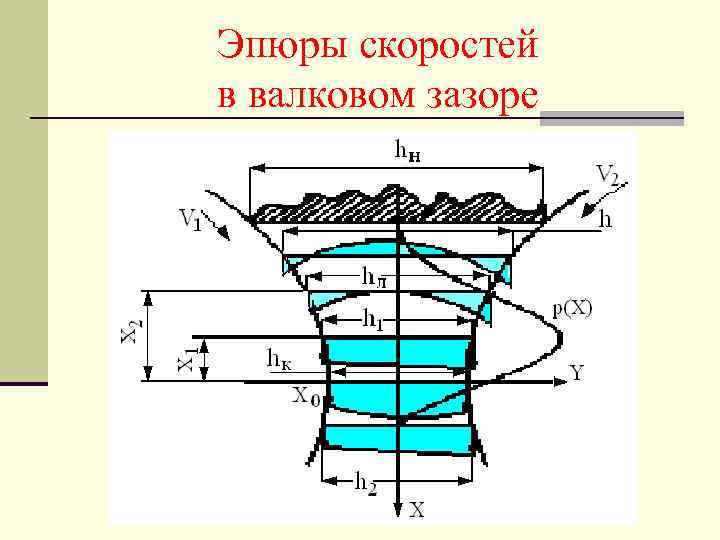
Эпюры скоростей в валковом зазоре

5. 1. 6. Смешение в закрытом роторном смесителе. n Рассматривается течение материала между двумя непараллельными плоскостями. При этом наклонная плоскость моделирует ротор, его горизонтальная часть – гребень ротора, а нижняя горизонтальная плоскость моделирует поверхность стенки камеры смесителя. Анализ проводится при целом ряде допущений, главные из которых следующие: чтобы система координат была неподвижной, принимается, что движется не ротор, а стенка корпуса; кривизной поверхности корпуса пренебрегаем; соблюдается условие прилипания: слои, прилегающие к стенке, движутся со скоростью стенки, слои, прилегающие к поверхности ротора, неподвижны.

Уравнение для расчета скорости h – расстояние между плоскостями; y 0 – ордината максимума скорости; U – скорость движения плоскости; n – индекс течения.

Эпюры скоростей в зазоре между двумя плоскостями

5. 2. Формование n 5. 2. 1. Общие сведения Под формованием понимается придание полимерному материалу определенной формы, требуемой для дальнейшего ведения технологического процесса или задаваемой условиями эксплуатации изделия. Формование осуществляется действием механических сил в сочетании с разогревом материала и реализуется в процессах экструзии, каландрования, прессования и литья под давлением.

5. 2. 2. Экструзия. n Экструзия – это технологический процесс, сущность которого состоит в превращении материала в изделие с поперечным сечением нужной формы путем продавливания материала через профилирующий инструмент (матрицу). n Основные зоны: зона питания (или зона загрузки) – участок, в котором перерабатываемый материал находится в твердом состоянии; зона сжатия (или зона пластикации, зона плавления) – участок, в котором почти полностью происходит плавление материала; зона дозирования – участок, в котором материал находится в вязкотекучем состоянии.
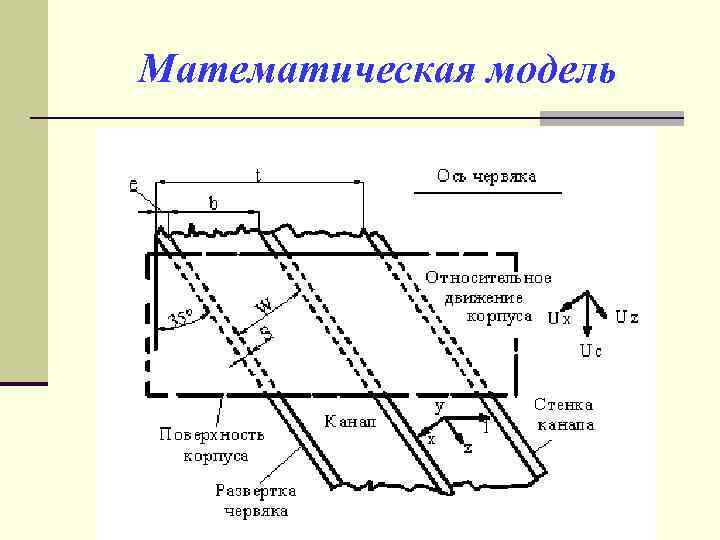
Математическая модель
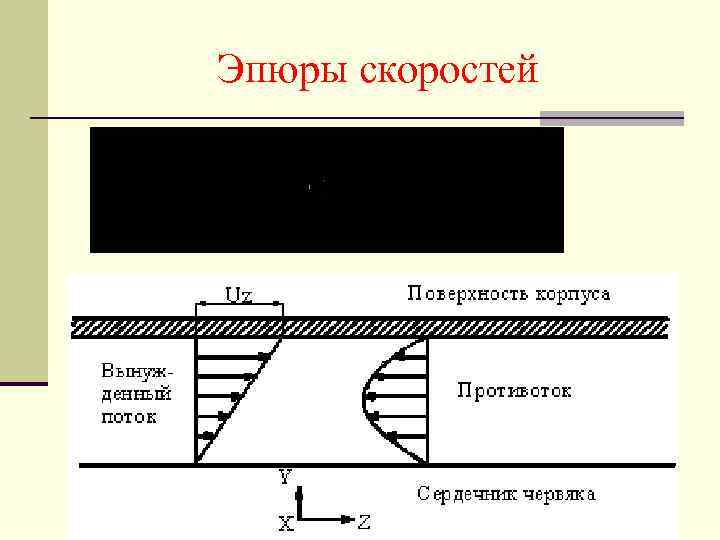
Эпюры скоростей
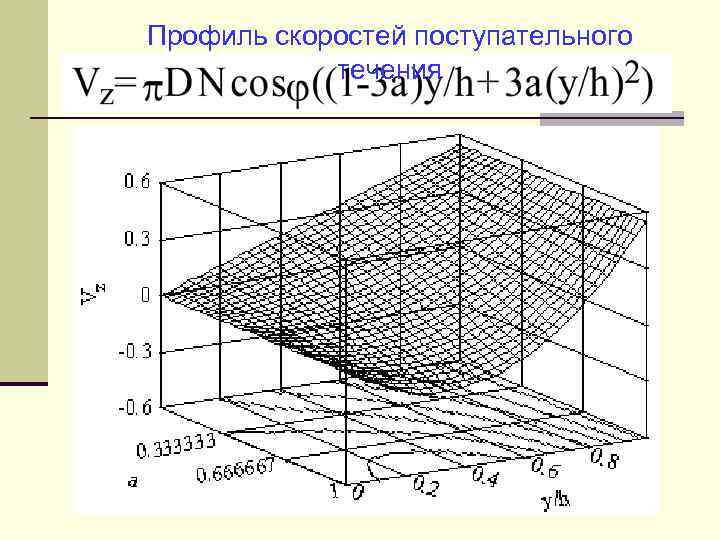
Профиль скоростей поступательного течения
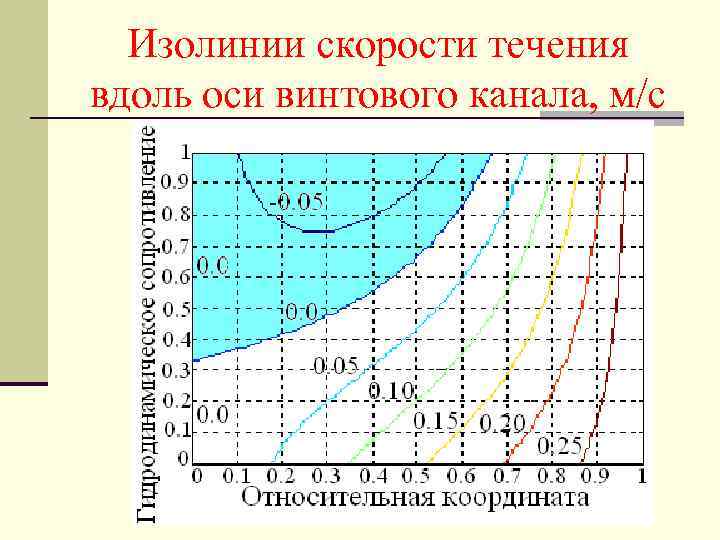
Изолинии скорости течения вдоль оси винтового канала, м/с
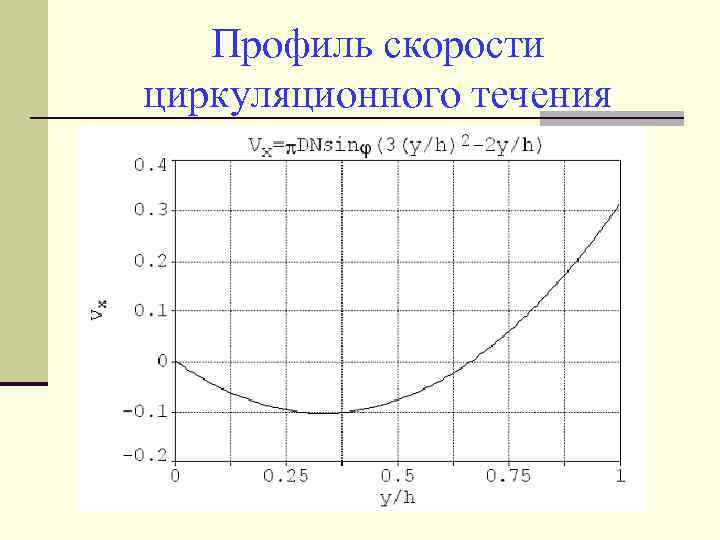
Профиль скорости циркуляционного течения
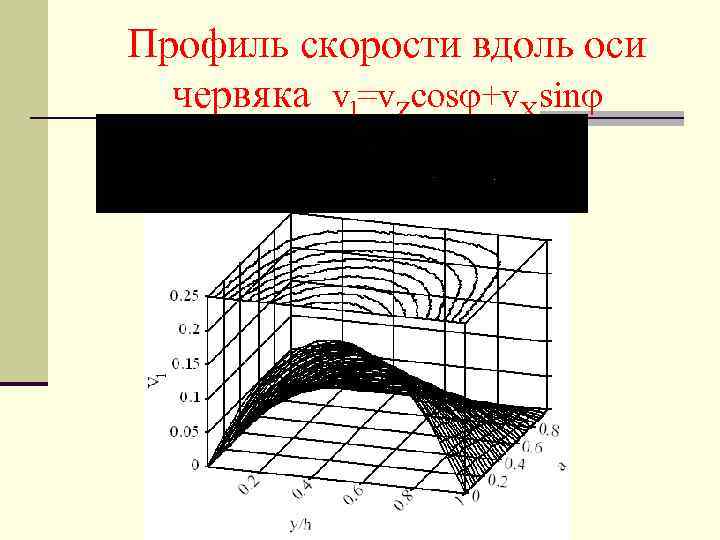
Профиль скорости вдоль оси червяка vl=v. Zcos +v. Xsin
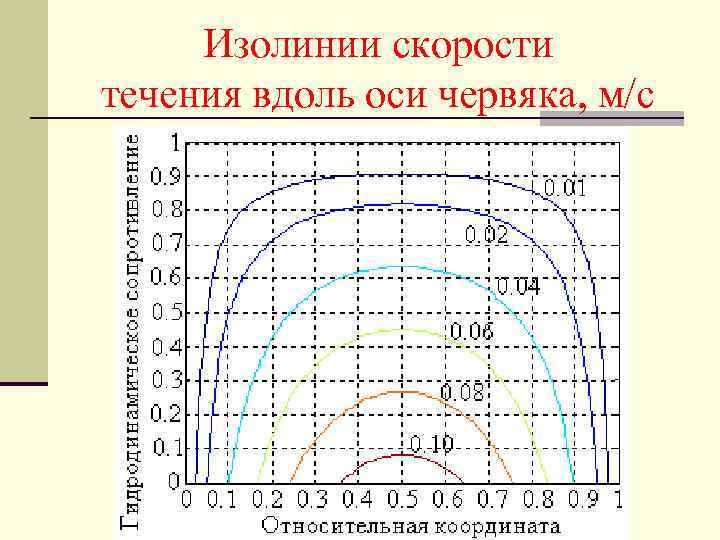
Изолинии скорости течения вдоль оси червяка, м/с

5. 2. 3. Литье под давлением n При формовании методом литья под давлением полимер вначале расплавляется, а затем под высоким давлением впрыскивается в полость закрытой формы. При литье термопластичного материала заполнявший форму расплав охлаждается и затвердевает, а затем форма открывается и изделие удаляется из формы. Если перерабатывают термореактивный материал, то впрыснутый в форму полимер нагревают до температуры отверждения (вулканизации) и выдерживают в течение времени, необходимого для полного отверждения изделия.
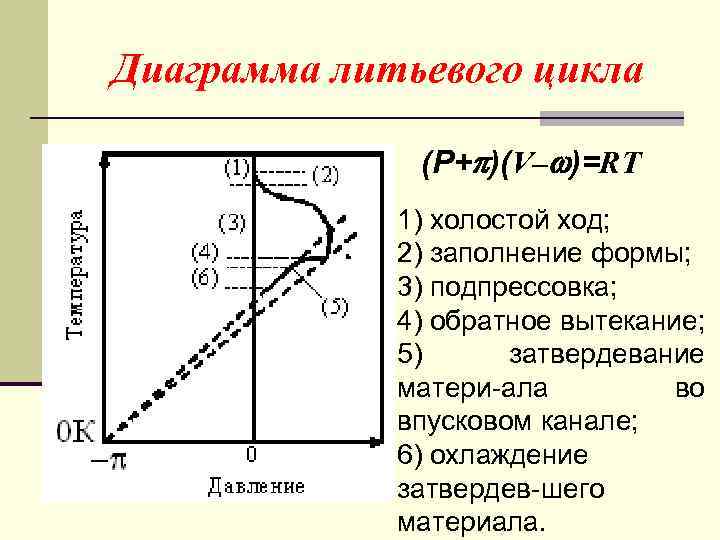
Диаграмма литьевого цикла (P+ )(V– )=RT 1) холостой ход; 2) заполнение формы; 3) подпрессовка; 4) обратное вытекание; 5) затвердевание матери-ала во впусковом канале; 6) охлаждение затвердев-шего материала.
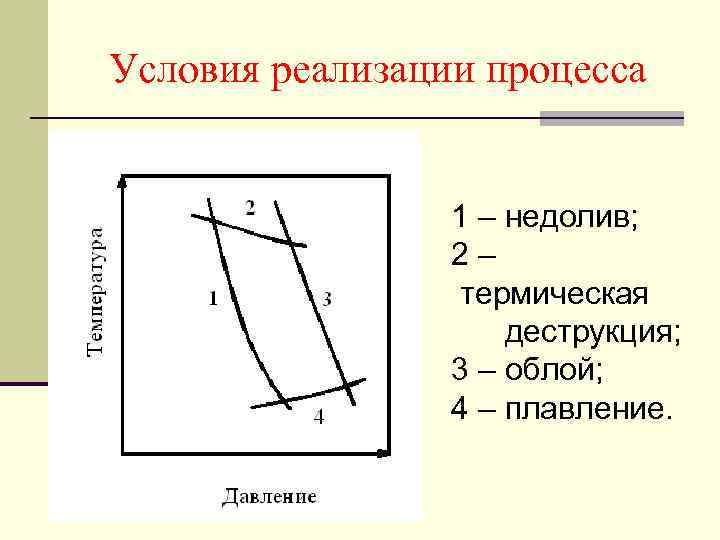
Условия реализации процесса 1 – недолив; 2 – термическая деструкция; 3 – облой; 4 – плавление.

Критерии формуемости n 1) жесткость; n 2) легкость выгрузки; n 3) минимальное количество дефектов; n 4) соответствие между формой гнезда и формой изделия; n 5) минимальная величина замороженных ориентационных деформаций, не выходящая за пределы допуска на геометрические размеры изделия.

Течение в круглой трубе
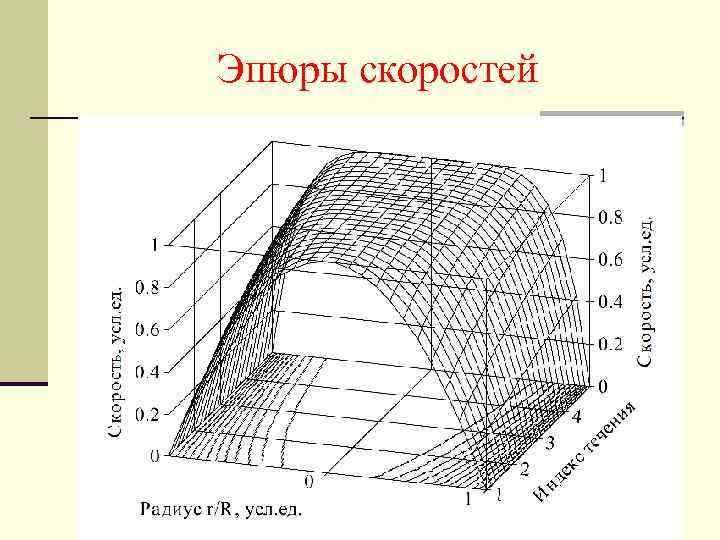
Эпюры скоростей
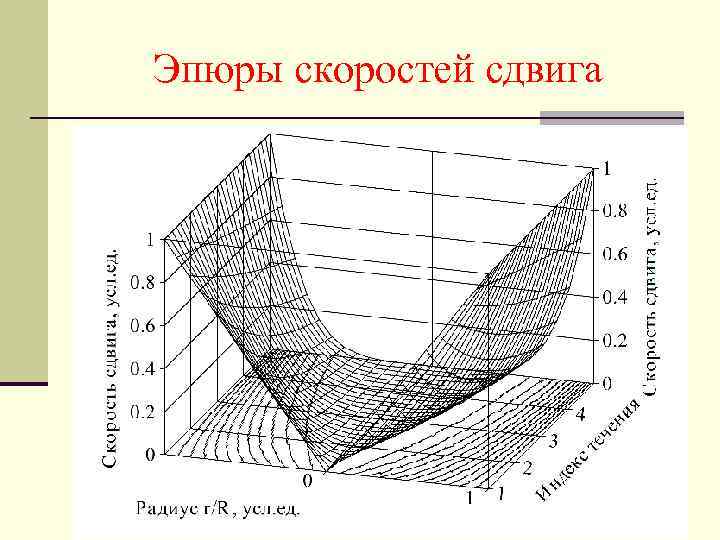
Эпюры скоростей сдвига

5. 3. Отверждение (вулканизация) n 5. 3. 1. Общие сведения. n Правило Вант-Гоффа K=k. T+5/k. T-5 n Уравнение Аррениуса Если считать, что k не зависит от T

Метод приращения эквивалентных времен Интенсивность процесса Эффективность (эффект) процесса Эквивалентное время

5. 3. 2. Оптимизация процесса вулканизации (отверждения). Для многослойной стенки
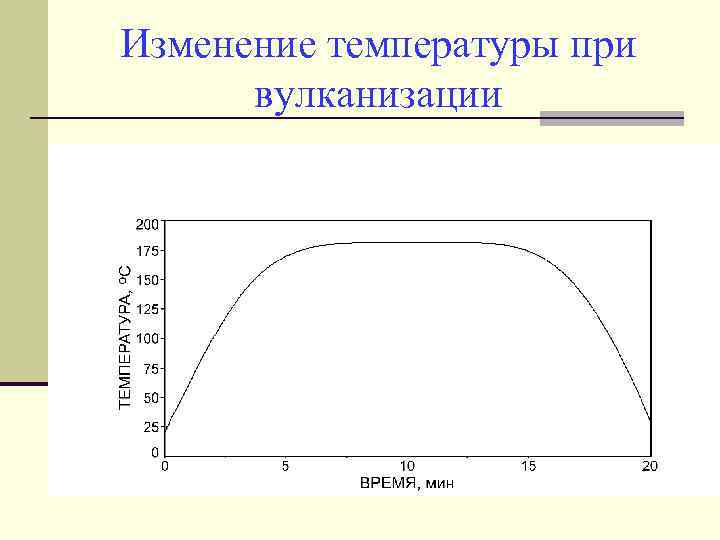
Изменение температуры при вулканизации
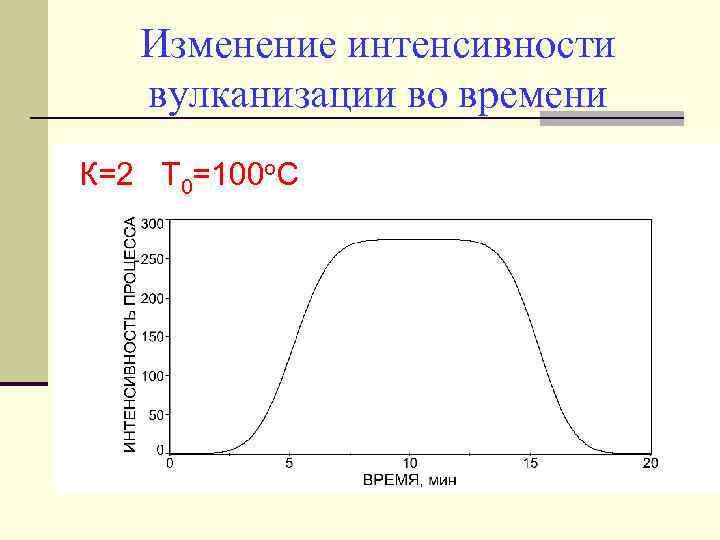
Изменение интенсивности вулканизации во времени К=2 Т 0=100 о. С
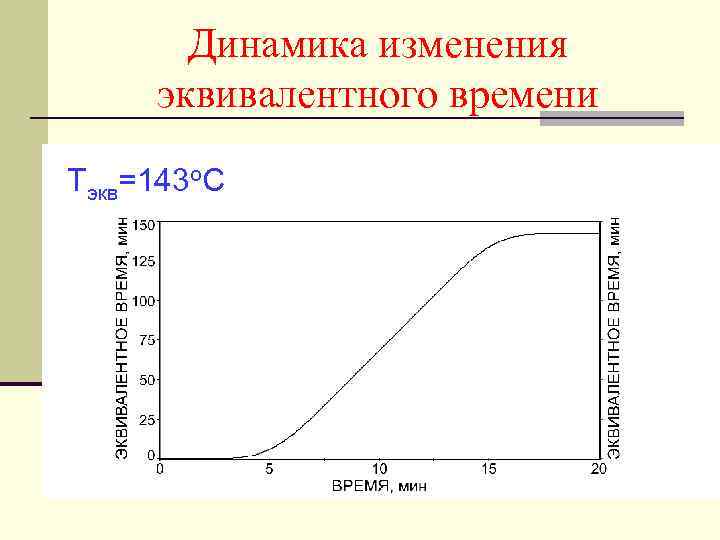
Динамика изменения эквивалентного времени Тэкв=143 о. С

Заключение n Подводя итог, следует отметить, что рассмотрение проблем моделирования химико-технологических процессов, вообще, в отрыве от конкретных особенностей объекта моделирования, было бы полезным для общего развития, но вряд ли позволило бы перекинуть эвристический «мостик» между общим и специфическим подходом «полимерного» характера. Данный курс следует рассматривать именно как такой «мостик» .
Моделирование.ppt