Моделирование социальных процессов Лекции для студентов спец ММЭ

Моделирование социальных процессов Лекции для студентов спец. ММЭ, з/о

1. Когнитивные подходы в моделировании социальных систем Определение. Под когнитивным подходом понимается решение традиционных для данной науки проблем методами, учитывающими процессы восприятия, мышления, познания, объяснения и понимания. Появление когнитологии: Гарвард, 1960 г. Когнитология междисциплинарное научное направление, объединяющее философию (теория познания), психологию, нейрофизиологию, антропологию, лингвистику и теорию искусственного интеллекта.

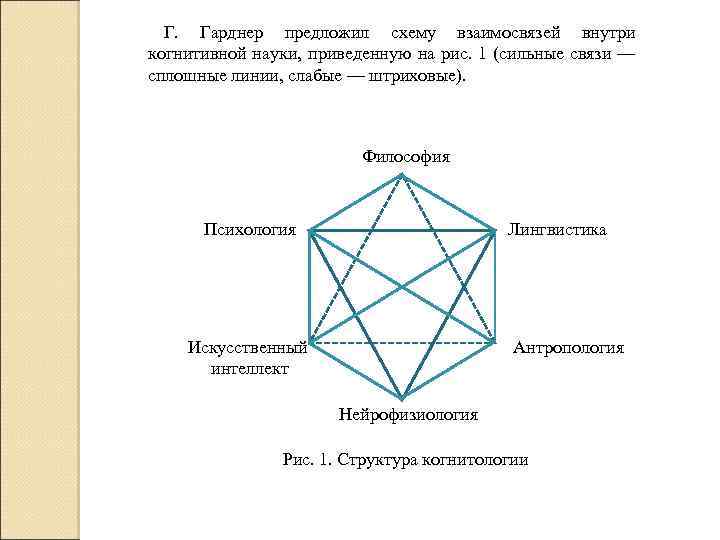Г. Гарднер предложил схему взаимосвязей внутри когнитивной науки, приведенную на рис. 1 (сильные связи — сплошные линии, слабые — штриховые). Философия Психология Лингвистика Антропология Искусственный интеллект Нейрофизиология Рис. 1. Структура когнитологии

Когнитивные карты Когнитивная карта множество вершин, каждая из которых соответствует одному фактору или элементу исследуемой системы. Дуга, связывающая вершины А и В, соответствует причинно следственной связи А —> В, где А — причина, В — следствие. Связь А—>В называется положительной (знак «+» ), если увеличение А ведет к увеличению (усилению) В, а уменьшение А ведет к уменьшению В при прочих равных условиях. Знак « » над дугой А—>В означает, что связь отрицательная, т. е. увеличение А приводит к уменьшению (торможению) В и уменьшение А ведет к увеличению В.

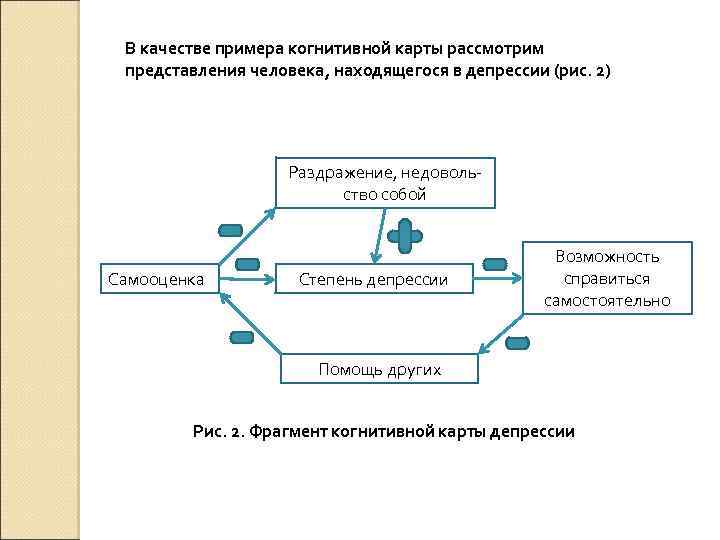В качестве примера когнитивной карты рассмотрим представления человека, находящегося в депрессии (рис. 2) Раздражение, недовольство собой Самооценка Степень депрессии Возможность справиться самостоятельно Помощь других Рис. 2. Фрагмент когнитивной карты депрессии

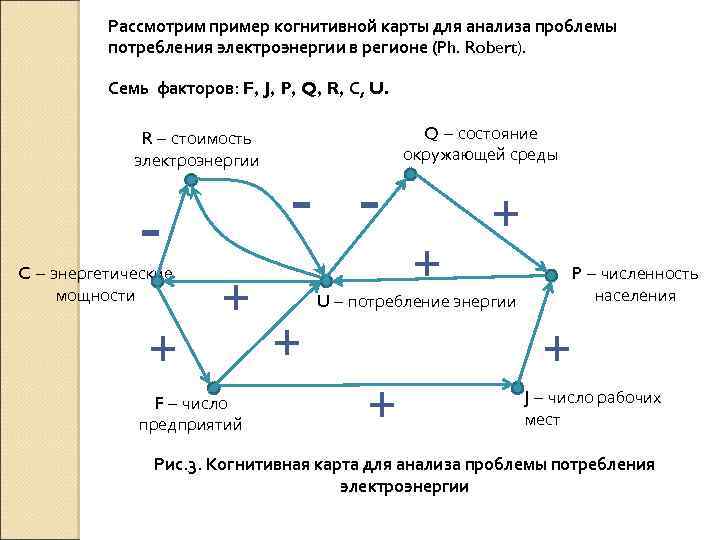Рассмотрим пример когнитивной карты для анализа проблемы потребления электроэнергии в регионе (Ph. Robert). Семь факторов: F, J, P, Q, R, С, U. R – стоимость электроэнергии - C – энергетические мощности + + F – число предприятий - + Q – состояние окружающей среды + + U – потребление энергии + P – численность населения + J – число рабочих мест Рис. 3. Когнитивная карта для анализа проблемы потребления электроэнергии

Когнитивная карта дает возможность проследить взаимосвязи между будущим, настоящим и прошлым изучаемого процесса. Использование когнитивных карт для планирования в организации может потребовать фиксации нескольких тысяч взаимосвязанных утверждений. Следовательно, для записи, хранения, поиска и анализа информации необходимо использовать ЭВМ и специальное программное обеспечение. В настоящее время разработан ряд коммерческих пакетов для анализа когнитивных карт (NIPPER, Cope, GISMO).

Задания для самостоятельного решения: 1. Попробуйте визуализировать свое отношение к изучению математики в виде когнитивной карты. Проанализируйте полученную когнитивную карту. Что необходимо предпринять для повышения качества обучения? 2. В работе К. Сайда с помощью когнитивной карты, изображенной на рис. 4, исследовалась динамика экономического роста типичной развивающейся страны и политическая нестабильность, связанная с борьбой за власть правительства и диссидентов. Попытайтесь самостоятельно расставить знаки и стрелки на дугах, выявив таким образом положительные и отрицательные связи, обоснуйте своё решение.

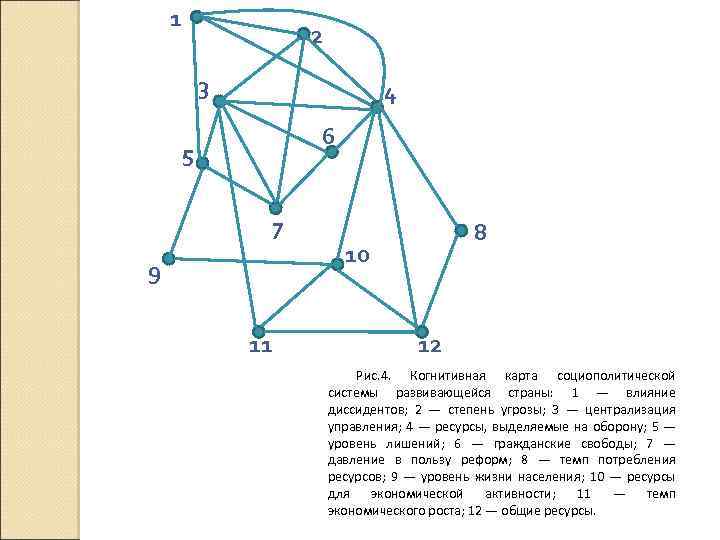1 2 3 4 6 5 7 9 11 8 10 12 Рис. 4. Когнитивная карта социополитической системы развивающейся страны: 1 — влияние диссидентов; 2 — степень угрозы; 3 — централизация управления; 4 — ресурсы, выделяемые на оборону; 5 — уровень лишений; 6 — гражданские свободы; 7 — давление в пользу реформ; 8 — темп потребления ресурсов; 9 — уровень жизни населения; 10 — ресурсы для экономической активности; 11 — темп экономического роста; 12 — общие ресурсы.

2. Математические модели социальных процессов, описываемые дифференциальными уравнениями и их системами 2. 1 Модели сотрудничества и борьбы за существование Лотки. Вольтерра Рассматривается система двух дифференциальных уравнений, описывающих взаимодействие двух популяций: d. Хl /dt = C 1 X 1 + al 2 X 1 X 2 + а 11 X 12, d. Х 2/dt = С 2 X 2+ a 2 l X 1 X 2 + а 22 X 1 (t) и X 2 (t) — численность популяций в момент t. Линейные члены C 1 X 1 и C 2 X 2 в правых частях уравнений cooтветствуют свободному размножению видов. Если коэффициент С > О, то численность соответствующего вида растет, если C < О, то численность уменьшается. Члены а 11 X 12 и а 22 X 22 отражают наличие внутривидовой конкуренции (при а 11 < О и а 22 < О) или процесса образования сообществ (если а 11 > О, а 22> О). Произведения факторов Х 1 X 2 отражают процесс взаимодействия двух популяций. Если коэффициенты al 2 , a 2 l отрицательны, то виды конкурируют друг с другом. При а 12 а 21 > О процесс взаимодействия биологи называют симбиозом (в социальной сфере более уместно говорить о сотрудничес тве, кооперации). Если а 12 > О и а 21 < О, то первый вид является хищником, а второй — жертвой (если численность первого вида больше, то это взаимодействие паразита с хозяином).

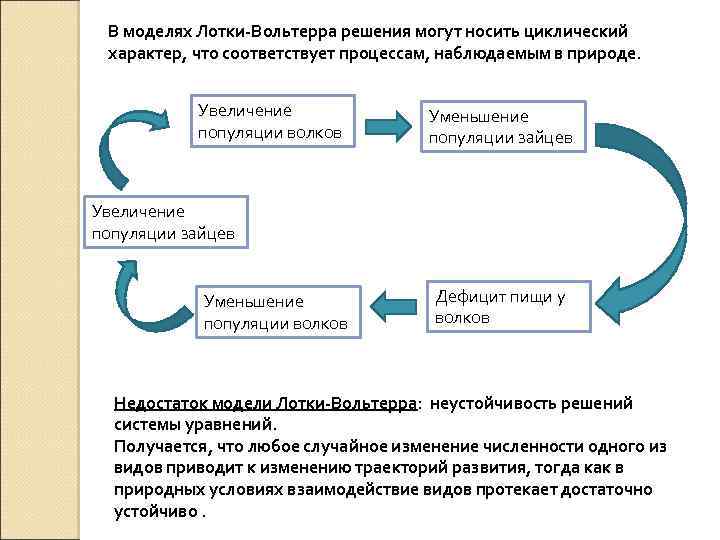В моделях Лотки-Вольтерра решения могут носить циклический характер, что соответствует процессам, наблюдаемым в природе. Увеличение популяции волков Уменьшение популяции зайцев Увеличение популяции зайцев Уменьшение популяции волков Дефицит пищи у волков Недостаток модели Лотки-Вольтерра: неустойчивость решений системы уравнений. Получается, что любое случайное изменение численности одного из видов приводит к изменению траекторий развития, тогда как в природных условиях взаимодействие видов протекает достаточно устойчиво.

2. 2 Модель гонки вооружений Ричардсона Пусть имеются две враждующие страны. Первая страна ("желтые") вооружается, опасаясь потенциальной угрозы войны с соседней враждебной страной ("зеленые"). В свою очередь "зеленые", зная о росте затрат на вооружение у "желтых", также увеличивают расходы на вооружение. Предположим, что каждая страна изменяет скорость роста (сокращения) вооружений пропорционально уровню затрат другой. Пусть x(t) — расходы на вооружение "желтых" к моменту t >0, y(t) — то же, но "зеленых". Простейшая модель гонки вооружений может быть сформулирована в виде системы двух линейных дифференциальных уравнений с постоянными коэффициентами: (1) Здесь а и b — положительные константы. Недостаток! Рост затрат на вооружение ничем не лимитируется!

Первое предположение Л. Ричардсона: чем больше текущий уровень затрат на оборону, тем меньше скорость его роста. (2) Здесь m и n — положительные константы. Второе предположение Л. Ричардсона: государство наращивает вооружение, руководствуясь своими державными притязаниями и враждебностью к другим государствам, даже если другие страны не угрожают существованию данного государства. Обозначим соответствующие коэффициенты претензии через r и s (r>0 и s>0). Если r<0 и s<0, то их можно назвать коэффициентами доброй воли.

Получаем следующую систему уравнений: (3) Элементарный анализ модели. Стабильность гонки вооружений - уровень затрат на вооружение постоянен и не зависит от времени. Пусть система находится в состоянии равновесия: (4)

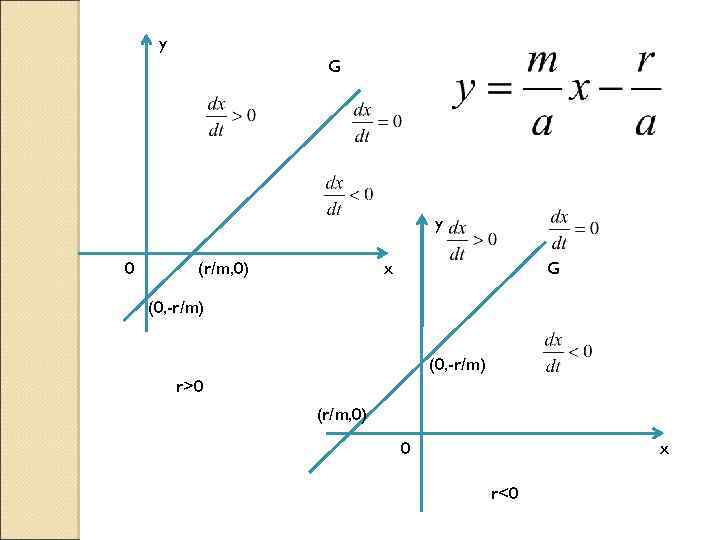
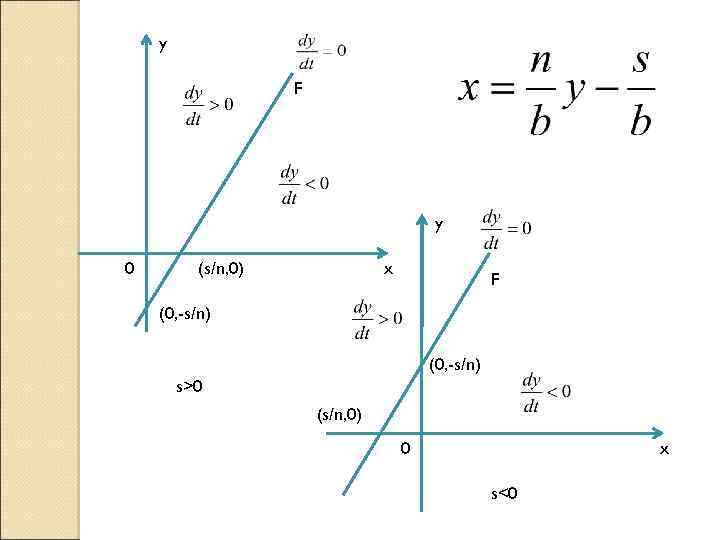
(5) (6) Рассмотрим геометрическую интерпретацию линейных уравнений (6) на фазовой плоскости (х, у).

y G y 0 (r/m, 0) x G (0, -r/m) r>0 (r/m, 0) 0 x r<0

y F y 0 (s/n, 0) x F (0, -s/n) s>0 (s/n, 0) 0 x s<0

y G I F II (x*; y*) r>0, s<0 IV III 0 x Рис. 5. Точка равновесия в первом квадранте

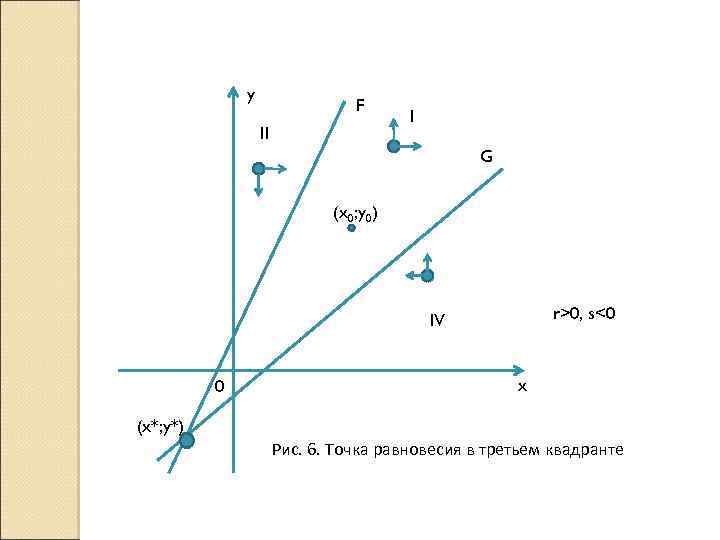y F II I G (x 0; y 0) r>0, s<0 IV 0 x (x*; y*) Рис. 6. Точка равновесия в третьем квадранте

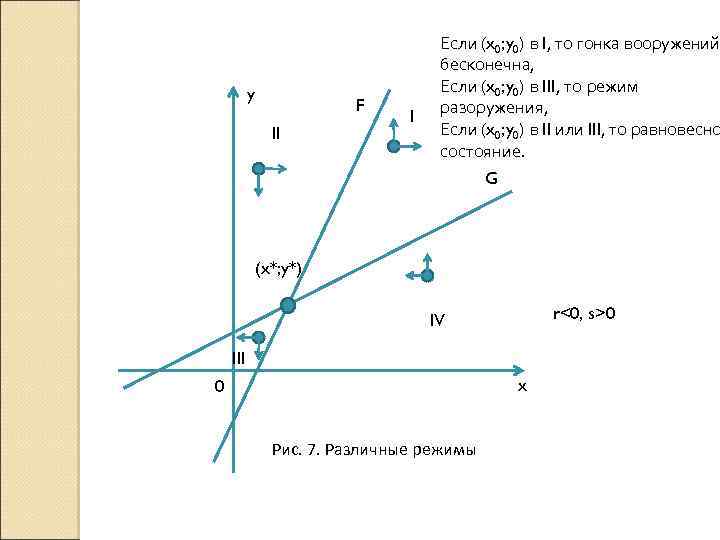y F II I Если (x 0; y 0) в I, то гонка вооружений бесконечна, Если (x 0; y 0) в III, то режим разоружения, Если (x 0; y 0) в II или III, то равновесно состояние. G (x*; y*) r<0, s>0 IV III x 0 Рис. 7. Различные режимы

Поведение модели Ричардсона зависит от соотношения коэффициентов а, Ь, т, п и знаков r, s. Показано, что имеют место четыре возможных варианта развития: 1. Если тп - ab > 0, r > 0, s > 0, то существует точка равновесия. 2. Если тп - ab < 0, r > 0, s > 0, то логика модели ведет к неограниченной эскалации гонки вооружений. 3. Если тп - ab > 0, r < 0, s < 0, то гарантируется полное взаимное разоружение. 4. Если тп - ab < 0, r < 0, s < 0, то пессимистичность или оптимистичность прогноза существенно зависит от начального состояния.

3. Модели принятия решений Теоретико-игровые модели конфликтных ситуаций Рассматривается проблемная ситуация, в которую вовлечены только два участника — А и В (два индивида, индивид и система или две социальные системы). Идея состоит в том, что каждый участник выбирает одну из двух альтернатив: С — сотрудничество, кооперация, солидарность, учет общих интересов, разрешение конфликта, альтруистическое поведение; D — отказ от сотрудничества, усиление конфронтации, обман, нарушение принятых норм, правил, обязательств, эгоистическое поведение. Результаты игры определяются с помощью следующей таблицы выигрышей (платежной матрицы).

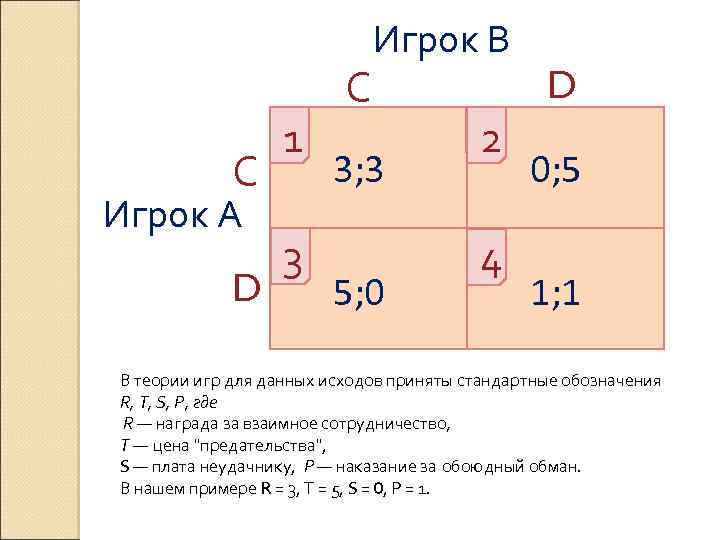С Игрок А D 1 3 С Игрок В 3; 3 5; 0 2 4 D 0; 5 1; 1 В теории игр для данных исходов приняты стандартные обозначения R, T, S, Р, где R — награда за взаимное сотрудничество, Т — цена "предательства", S — плата неудачнику, Р — наказание за обоюдный обман. В нашем примере R = 3, Т = 5, S = 0, P = 1.

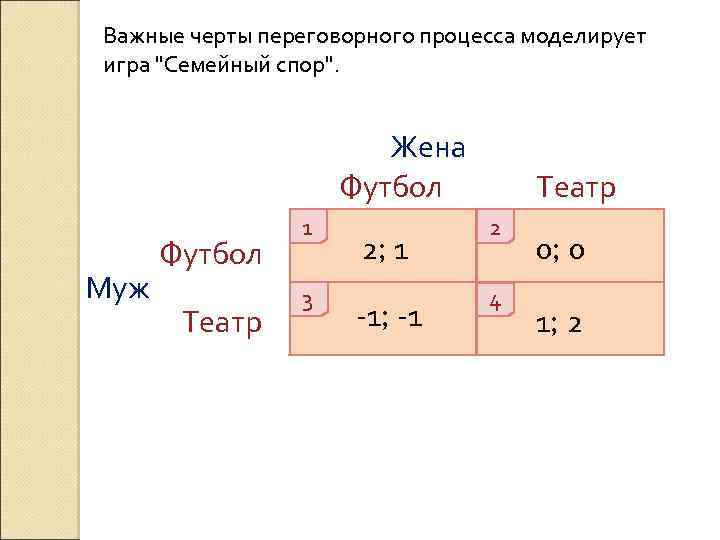Важные черты переговорного процесса моделирует игра "Семейный спор". Жена Футбол Муж Футбол Театр 1 3 2; 1 -1; -1 Театр 2 4 0; 0 1; 2

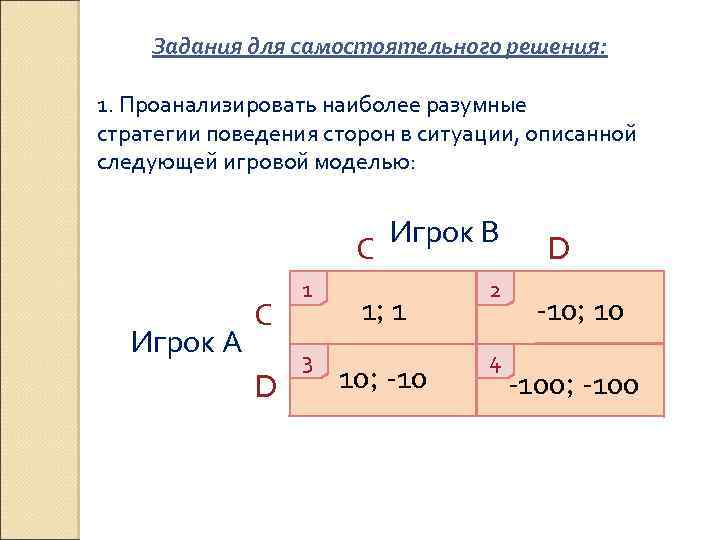Задания для самостоятельного решения: 1. Проанализировать наиболее разумные стратегии поведения сторон в ситуации, описанной следующей игровой моделью: С Игрок А С D 1 3 Игрок В 1; 1 10; -10 2 4 D -10; 10 -100; -100

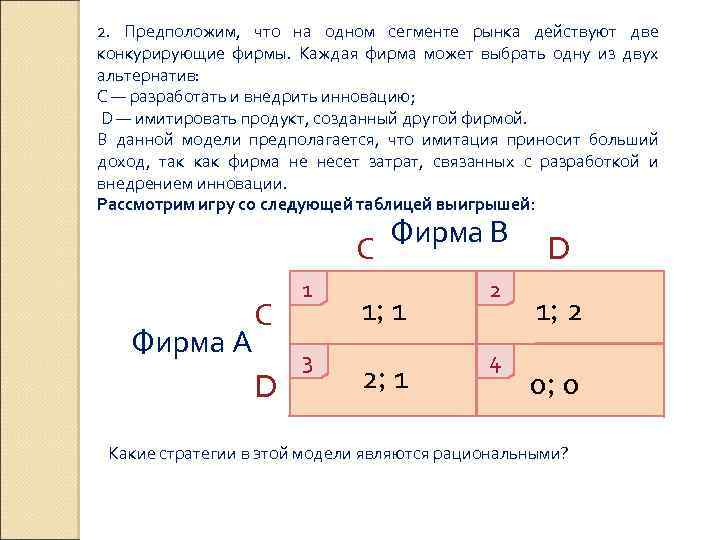2. Предположим, что на одном сегменте рынка действуют две конкурирующие фирмы. Каждая фирма может выбрать одну из двух альтернатив: С — разработать и внедрить инновацию; D — имитировать продукт, созданный другой фирмой. В данной модели предполагается, что имитация приносит больший доход, так как фирма не несет затрат, связанных с разработкой и внедрением инновации. Рассмотрим игру со следующей таблицей выигрышей: С Фирма А С D 1 3 Фирма В 1; 1 2 4 D 1; 2 0; 0 Какие стратегии в этой модели являются рациональными?

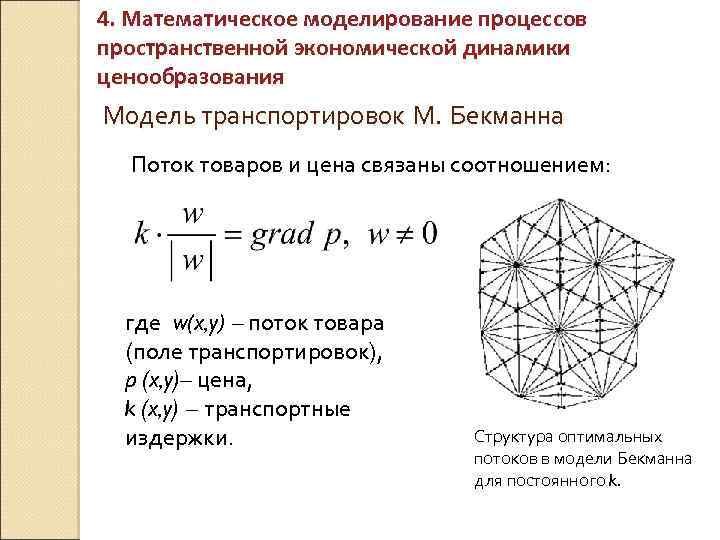4. Математическое моделирование процессов пространственной экономической динамики ценообразования Модель транспортировок М. Бекманна Поток товаров и цена связаны соотношением: где w(x, y) – поток товара (поле транспортировок), p (x, y)– цена, k (x, y) – транспортные издержки. Структура оптимальных потоков в модели Бекманна для постоянного k.

Зависимости, приводящие к модели ценообразования q Закон сохранения товара: q Динамика цены: q Динамика изменения количества товара: q Зависимость плотности потока товара: q Уравнение для цены: T(x, y, t) – плотность товара, Q(x, y, t) – плотность разности объемов производства и потребления товара, p(x, y, t) – цена, ξ – эластичность предложения товара, w(x, y, t) – плотность потока товара, k(x, y) – коэффициент «товарной проводимости» , D – объем спроса, S – объем предложения.

Математическая модель пространственного ценообразования: или граничное условие I рода. Коэффициент товарной проводимости k(x, y): - характеристика транспортного средства; - энергетические затраты транспортного средства; - безопасность пути; - масса груза; - затраты на обслуживание груза в пути; - географические характеристики; - прочее.

Задачи управления A. Распределённое управление, граничное наблюдение - плотность разности объемов производства и потребления товара q Контроль (государственный контроль) над ценами вывозимой продукции; q Внутренний (межрегиональный) контроль.

Задачи управления B. Распределённое управление, финальное наблюдение - плотность разности объемов производства и потребления товара q Контроль (государственный контроль) над ценами перевозимой продукции на период вперед.

Задачи управления С. Стартовое управление, финальное наблюдение q Контроль (государственный контроль) по установлению “потолков” первичных цен на продукцию, борьба с картельным сговором.

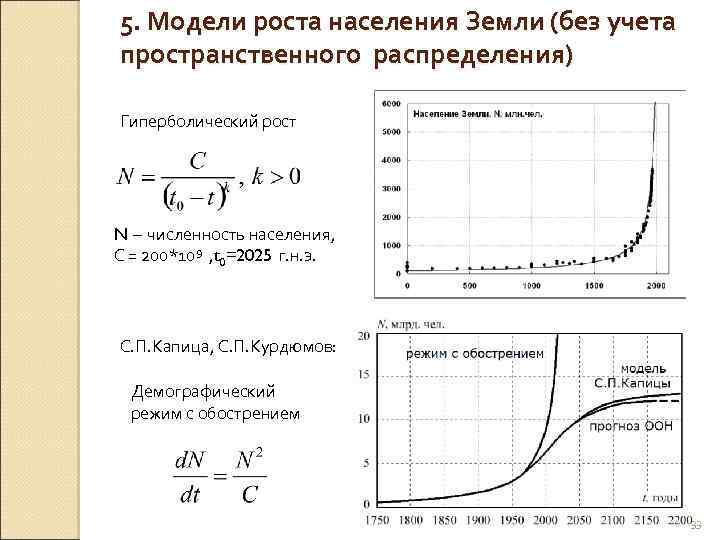5. Модели роста населения Земли (без учета пространственного распределения) Гиперболический рост N – численность населения, С = 200*109 , t 0=2025 г. н. э. С. П. Капица, С. П. Курдюмов: Демографический режим с обострением 33

Модель роста народонаселения с учетом пространственного распределения C(N) и Q(N) – некоторые функции пространственной плотности населения N(x , t). C 0, Q 0 – коэффициенты, допускающие независимую оценку.

Прогнозирование социальноэкономических процессов

Временной ряд и тренд 2009 г. Пример временного ряда Янв Демогр. прирост насел. в регионе (чел) Фев Мар Апр Май Июн Июл Авг Сен Окт Ноя Дек 1124 1203 1097 1021 1298 1051 1321 1211 1179 1342 1432 1091 1600 1400 1200 1000 800 Series 1 600 400 200 0 1 2 3 4 5 6 7 8 9 10 11 12 Тренд (trend) функциональная зависимость, описывающая тенденцию развития процесса

1. ВЫЯВЛЕНИЕ ТРЕНДА Во временных рядах социально-экономических явлений могут наблюдаться тенденции трех типов. 1. Тенденция среднего уровня, она может быть выражена графически. Аналитическая тенденция выражается некоторой математической функцией y = f (t) , вокруг которой варьируют эмпирические значения исходного временного ряда изучаемого явления. При этом значения, полученные на основе тренда, являются математическими ожиданиями временного ряда. 2. Тенденция дисперсии, она представляет собой тенденцию изменения отклонений эмпирических значений уровней временного ряда от теоретических, полученных по уравнению тренда. 3. Тенденция автокорреляции, выражающая тенденцию изменения корреляционной связи между отдельными, последовательными уровнями временного ряда.

Существуют различные методы обнаружения тенденций: 1. Проверка разности средних уровней Метод разработан для малых выборок (n<100). Ряд разбивается приблизительно на две равные части, которые рассматриваются как две независимые выборочные совокупности. Для каждой из них рассчитываются средние y 1_ср и y 2_ср и проверяется гипотеза о существенности разности y 1_ср –y 2_ср. Проверка гипотезы проводится по критерию Стьюдента.

2. Проверка гипотезы об отсутствии тенденции в дисперсиях во временном ряду Проверка осуществляется посредством проверки гипотезы о равенстве дисперсий двух совокупностей. Для проверки вычисляем расчетное значение F-критерия Фишера по формуле: Проверка гипотезы осуществляется на основе сравнения расчетного и критического значений F-критерия, полученного при заданном уровне значимости α и числах степеней свободы ν 1 и ν 2. Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей отвергается, если Fp>Fкр. Следовательно, расхождение между вычисленными дисперсиями значимо, носит неслучайный характер и в ряду динамики существует тенденция в дисперсиях и существует тренд. Данный метод дает приемлемые результаты в случае рядов с монотонной тенденцией.

3. Проверка ранговой корреляции Коэффициент ранговой корреляции где Q – число пар уровней временного ряда, у которых yt >yt+i (i = 1, 2, . . . , n-t) для всех t=1, 2, . . . , n-1, n – число уровней ряда. Коэффициент ранговой корреляции изменяется в пределах от -1 до +1. Значения r, близкие к -1, свидетельствуют о наличии отрицательного тренда, близкие к +1 – положительного тренда, близкие к 0 – об отсутствии тренда.

Кривые роста (регрессии) Кривые роста, описывающие закономерности развития явлений во времени, получают путем аналитического выравнивания временных рядов. Они представляют однофакторные модели прогнозирования (фактором выступает время). 1. Полиномы (многочлены). 2. Экспоненты. 3. Логистические кривые. 1. Полином (многочлен). Общий вид многочлена:

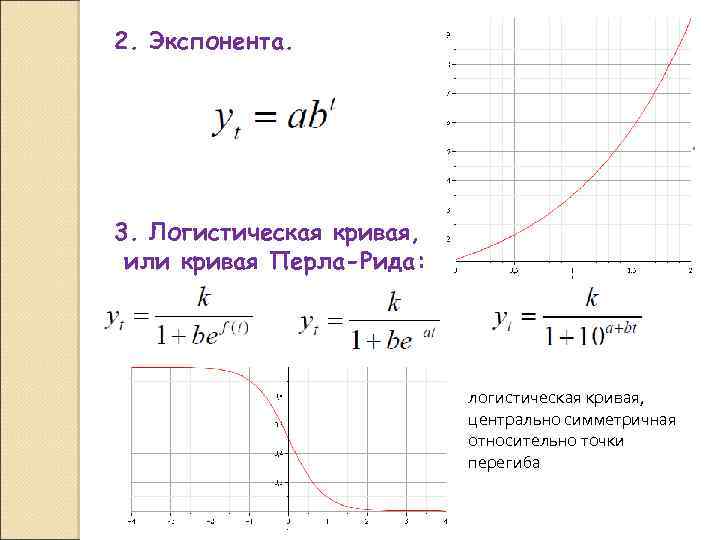2. Экспонента. 3. Логистическая кривая, или кривая Перла-Рида: логистическая кривая, центрально симметричная относительно точки перегиба

Метод наименьших квадратов Создатель: Карл Фридрих Гаусс в 18 -19 вв. Рассмотрим метод наименьших квадратов на простом примере зависимости между двумя переменными x и y, причем y зависит от x. Если установлено, что связь между ними криволинейная и описывается полиномом второй степени то задача сводится к отысканию неизвестных трех параметров a 0, a 1 и a 2. Пусть значения величин x и y представлены двумя рядами данных

Если бы все значения, полученные по данным наблюдения, лежали строго на линии (праболе), описываемой уравнением параболы, то для каждой точки xt было бы справедливо следующее равенство: Однако в действительности Необходимо найти такие коэффициенты регрессии, чтобы ошибка была минимальной. Оптимальным подходом является минимизация квадрата отклонений:

Прогнозирование на основе анализа временных рядов

Экстраполяция - продление на перспективу тенденций, наблюдавшихся в прошлом. Экстраполяция базируется на следующих допущениях: 1) развитие явления может быть достаточо хорошо охарактеризовано плавной траекторией – трендом; 2) общие условия, определяющие тенденцию развития в прошлом, не претерпят существенных изменений в будущем. Рис. 1. Экстраполяция траектории движения брошенного шарика

Процесс экстраполяции можно интерпретировать в виде последовательного определения значений функции: где - экстраполируемое значение уровня, - уровень, принятый за базу экстраполяции; L f – период упреждения. – трендовая кривая (регрессионная кривая роста).

Пример

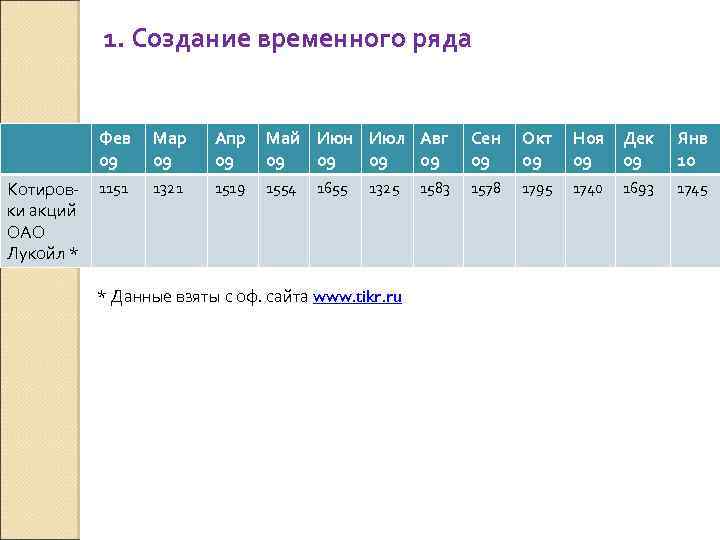1. Создание временного ряда Фев 09 Котировки акций ОАО Лукойл * Мар 09 Апр 09 Май Июн Июл Авг 09 09 Сен 09 Окт 09 Ноя Дек 09 09 Янв 10 1151 1321 1519 1554 1578 1795 1740 1745 1655 1325 * Данные взяты с оф. сайта www. tikr. ru 1583 1693

2. Выявление наличия тренда Проверим ранговую корреляцию. Вычислим коэффициент ранговой корреляции где Q – число пар уровней временного ряда, у которых yt >yt+i (i = 1, 2, . . . , n-t) для всех t=1, 2, . . . , n-1, n – число уровней ряда. Коэффициент ранговой корреляции изменяется в пределах от -1 до +1. Значения r, близкие к -1, будут свидетельствать о наличии отрицательного тренда, близкие к +1 – положительного тренда, близкие к 0 – об отсутствии тренда. Q=10, n=12, r=1 -4*10/(12*11) = 1 -40/132 = 0, 6969 => имеется положительный (растущий) тренд!

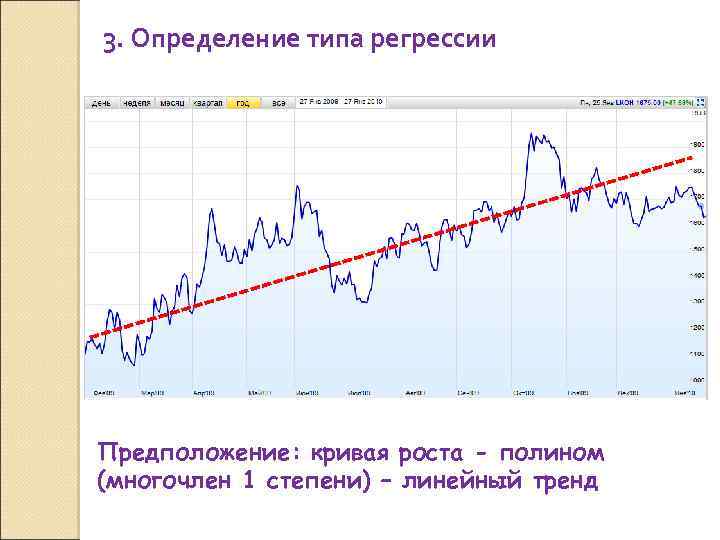3. Определение типа регрессии Предположение: кривая роста - полином (многочлен 1 степени) – линейный тренд

4. Построение прогноза

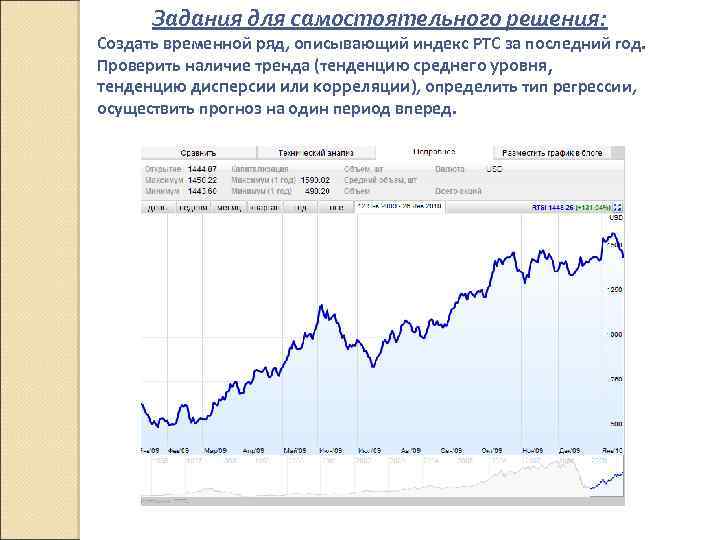Задания для самостоятельного решения: Создать временной ряд, описывающий индекс РТС за последний год. Проверить наличие тренда (тенденцию среднего уровня, тенденцию дисперсии или корреляции), определить тип регрессии, осуществить прогноз на один период вперед.

Нейронные сети (нейросети)

Введение Идея создания искусственного интеллекта возникла давно. Нейронные сети, экспертные системы, computer vision и т. д. – различные составляющие науки об ИИ. Главная цель науки о нейронных сетях – как можно более точно смоделировать процесс функционирования биологических нейронных сетей человеческого мозга.

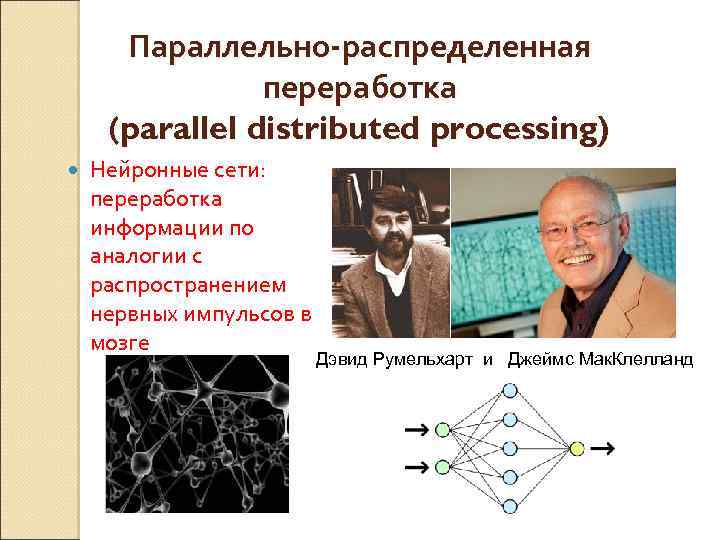Параллельно-распределенная переработка (parallel distributed processing) Нейронные сети: переработка информации по аналогии с распространением нервных импульсов в мозге Дэвид Румельхарт и Джеймс Мак. Клелланд

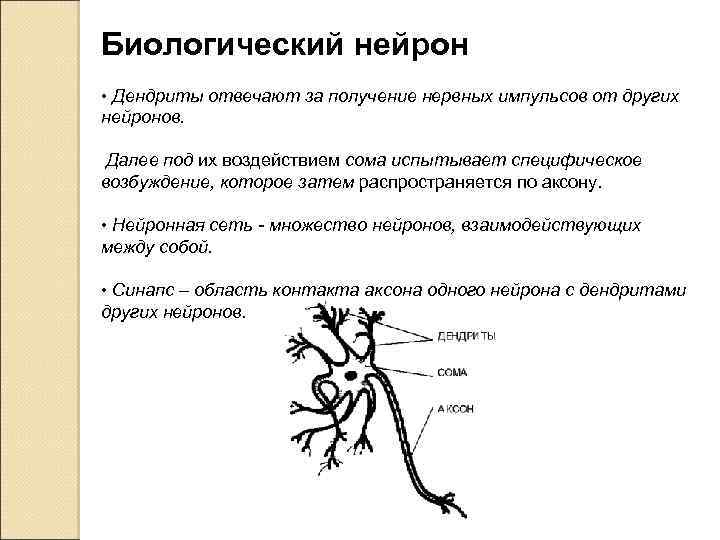Биологический нейрон • Дендриты отвечают за получение нервных импульсов от других нейронов. Далее под их воздействием сома испытывает специфическое возбуждение, которое затем распространяется по аксону. • Нейронная сеть - множество нейронов, взаимодействующих между собой. • Синапс – область контакта аксона одного нейрона с дендритами других нейронов.

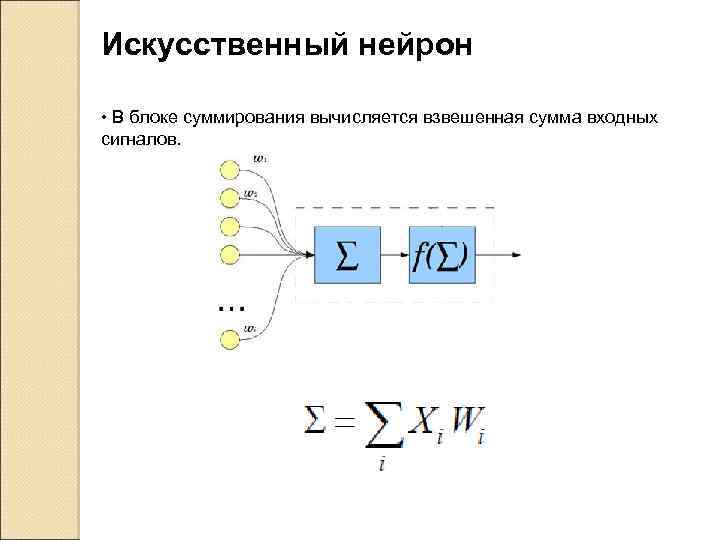Искусственный нейрон • В блоке суммирования вычисляется взвешенная сумма входных сигналов.

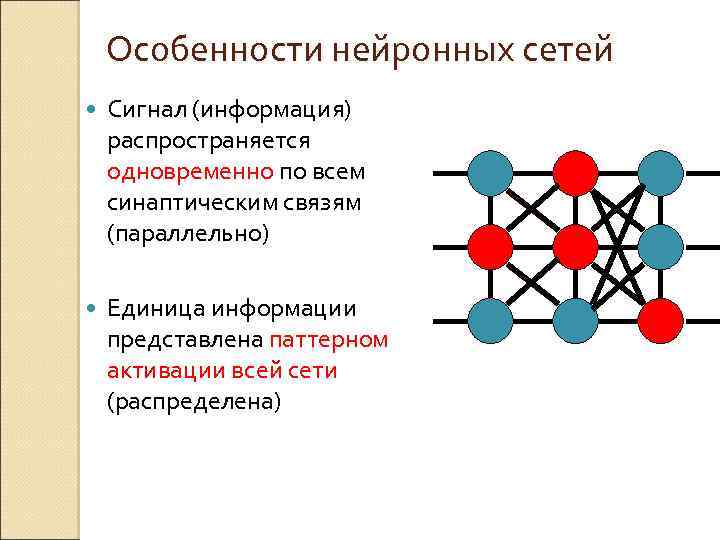Особенности нейронных сетей Сигнал (информация) распространяется одновременно по всем синаптическим связям (параллельно) Единица информации представлена паттерном активации всей сети (распределена)

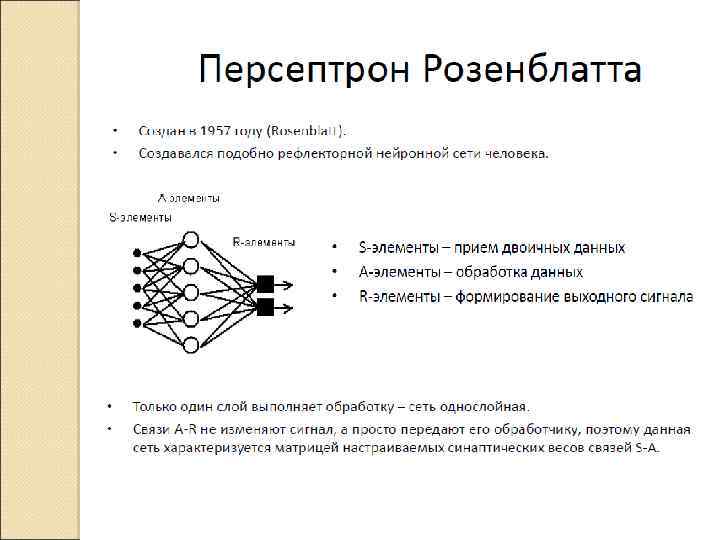
Прогнозирование с помощью аппарата нейросетей Deductor Studio (Academic Version), Free Download