Моделирование случайных воздействий на системы Выполнил студент гр

Моделирование случайных воздействий на системы Выполнил: студент гр. 1192 Новицкая С. В.

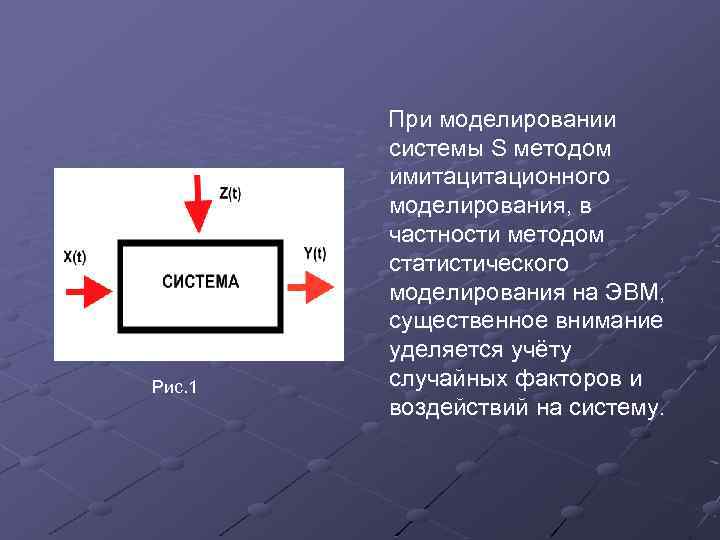Рис. 1 При моделировании системы S методом имитационного моделирования, в частности методом статистического моделирования на ЭВМ, существенное внимание уделяется учёту случайных факторов и воздействий на систему.

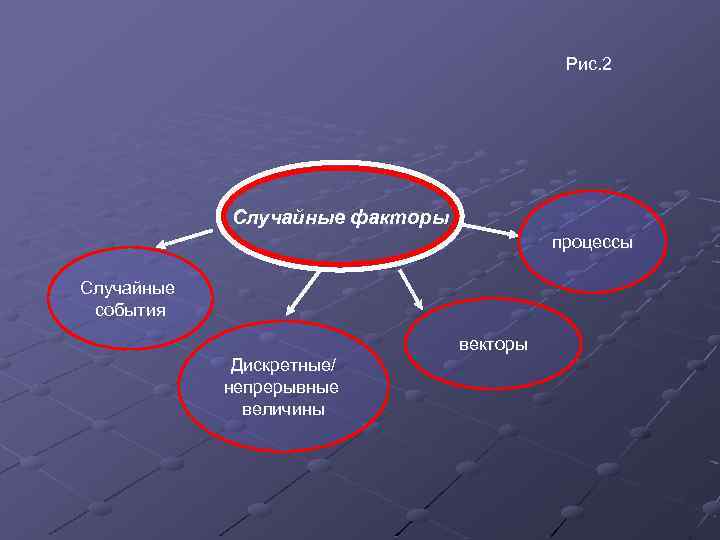Рис. 2 Случайные факторы процессы Случайные события векторы Дискретные/ непрерывные величины

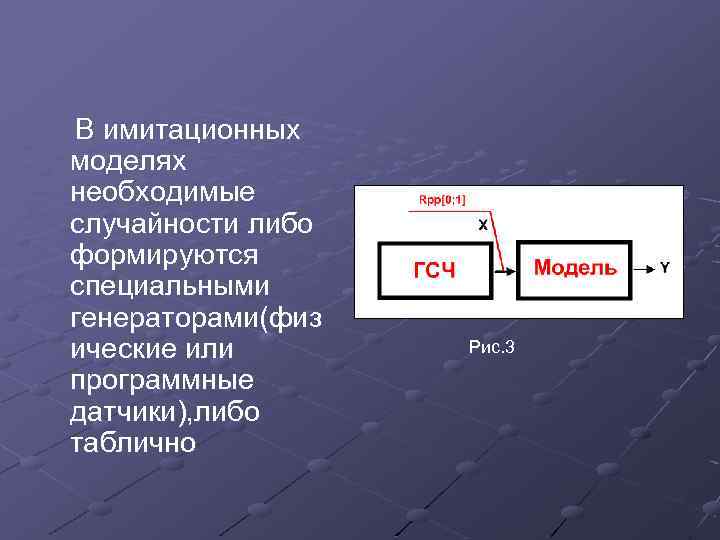В имитационных моделях необходимые случайности либо формируются специальными генераторами(физ ические или программные датчики), либо таблично Рис. 3

1. Способы моделирования случайных событий A- случайное событие с заданной P(A)=p: Ri ∈ R [0, 1] , Ri ≤ p Рис. 4 (1) ;

A 1, A 2, …, Ar - полная группа событий ↔ p 1 + p 2 +…+ pr=1: Ak- исход испытания ↔ k-1 k ∑ pi ≤ Ri ≤ ∑ pi i=1 Рис. 5 (2) ;

1. 1 Моделирование простой однородной цепи Маркова P 1 (0), P 2(0), … , Pk(0)начальные вероятности; P Ij - условная вероятность наступления Aj при условии , что исходом предыдущего испытания было событие Ai; A 1, A 2, . . , Ak - возможные исходы испытаний ;

k-1 i-е состояние: k ∑pi(0) ≤ Ri ≤ ∑pi(0) (3), i=1 Ri ∈ R [0, 1]; k-1 j-e состояние: k ∑pi 1(0) ≤ Ri+1 ≤ ∑pik(0) i=1 И т. д. (4),

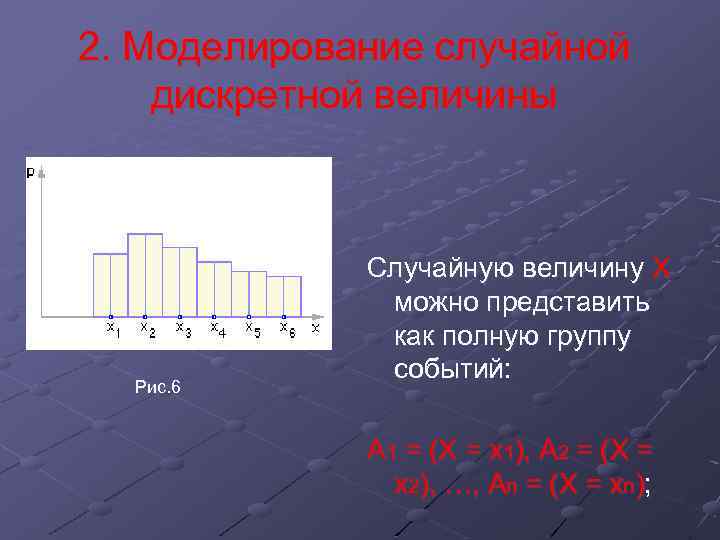2. Моделирование случайной дискретной величины Рис. 6 Случайную величину X можно представить как полную группу событий: А 1 = (Х = х1), А 2 = (Х = х2), …, Аn = (Х = хn);

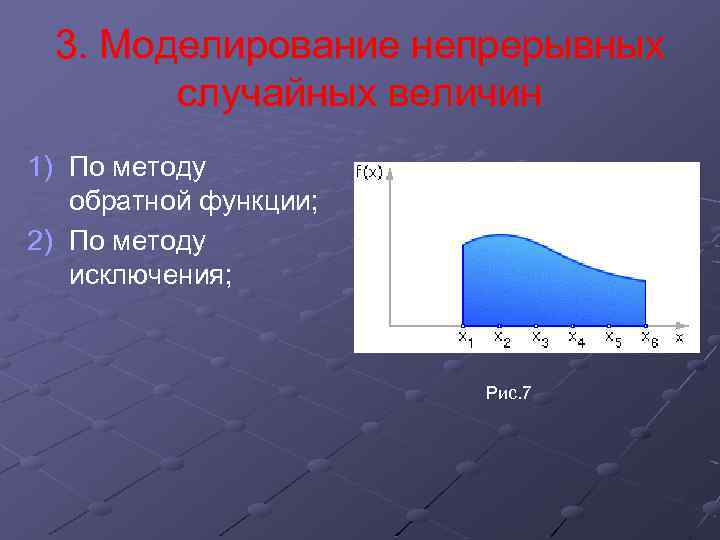3. Моделирование непрерывных случайных величин 1) По методу обратной функции; 2) По методу исключения; Рис. 7

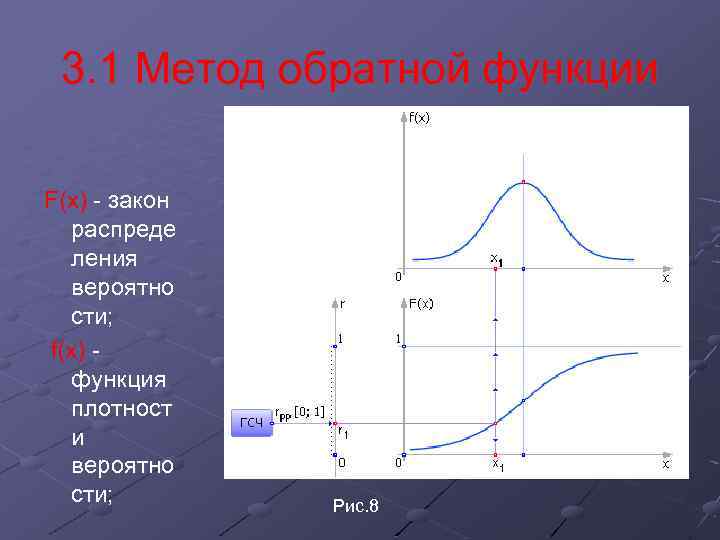3. 1 Метод обратной функции F(x) - закон распреде ления вероятно сти; f(x) функция плотност и вероятно сти; Рис. 8

Таким образом, последовательность r 1, r 2, r 3, . . , принадлежащая R(0, 1), преобразуется в последовательность х1, х2, х3. . . , которая имеет заданную функцию плотности распределения f(x).

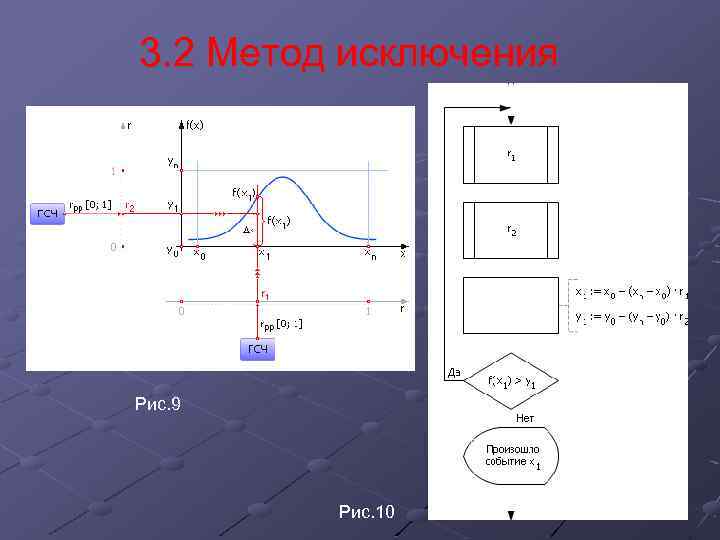3. 2 Метод исключения Рис. 9 Рис. 10

Спасибо за внимание! : -)