Моделирование процессов на поверхности Многоцентровая адсорбция
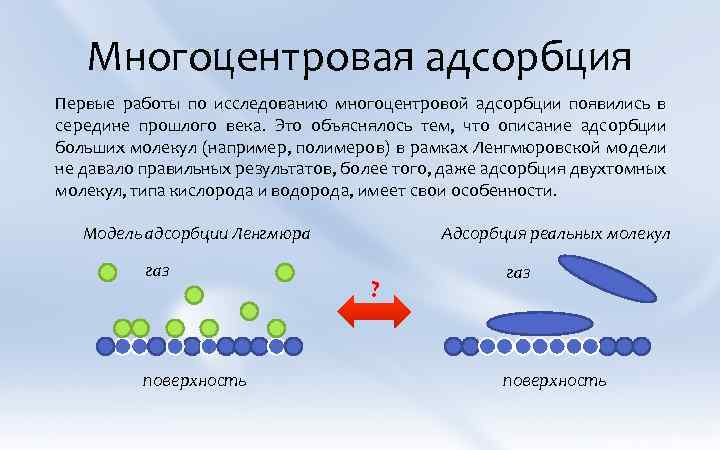
Многоцентровая адсорбция Первые работы по исследованию многоцентровой адсорбции появились в середине прошлого века. Это объяснялось тем, что описание адсорбции больших молекул (например, полимеров) в рамках Ленгмюровской модели не давало правильных результатов, более того, даже адсорбция двухтомных молекул, типа кислорода и водорода, имеет свои особенности. Модель адсорбции Ленгмюра газ поверхность Адсорбция реальных молекул ? газ поверхность
Многоцентровая адсорбция
Многоцентровая адсорбция Систематическое исследование многоцентровой адсорбции началось сравнительно недавно, около двадцати лет назад. Это связано с двумя вещами – с развитием экспериментальной техники и обнаружением интересных свойств таких адсорбционных монослоев. Например, процессы самоорганизации в адсорбционных – представляют большой интерес с точки зрения возможных применений для создания химических сенсоров, создания поверхностей с заданными свойствами, молекулярной электроники и др. Многие промышленно важные гетерогенные каталитические процессы проходят с участием сложных органических молекул, и исследование поведения таких адсорбционных слоев позволяет понять механизм протекания этих реакций.
Основные положения Простейшая модель многоцентровой адсорбции легко может быть построена в рамках МРГ. Единственное отличие от модели одноцентровой адсорбции заключается в предположении, что адсорбированная молекула занимает теперь несколько узлов решетки, образующих определенную конфигурацию. Однако такое предположение серьезно затрудняет теоретический анализ многоцентровой адсорбции, это связано с тремя факторами: 1) нет статистической эквивалентности между частицей и вакансией; 2) любой занятый узел указывает на то, что по крайней мере один из соседних узлов тоже занят; ? ? ? ? ? 3) нельзя точно определить, произойдет ли адсорбция на данной изолированной вакансии. ?
Моделирование многоцентровой адсорбции В связи с большой сложностью - точные решения моделей многоцентровой адсорбции возможны лишь в редких случаях, по этой причине зачастую используются приближенные методы: 1. Кластерный подход (например, приближение среднего поля, квазихимическое приближение). 2. Приближенные интегральные уравнения для корреляционных функций. 3. Разложение в ряд по степеням подходящей переменной. 4. Метод ренорм-группы. В этом методе вычисление статистической суммы выполняется последовательными этапами, причем на каждой ступени ренормализационный гамильтониан определяется заново. 5. Имитационное моделирование с помощью метода Монте-Карло. 6. Метод трансфер-матрицы.
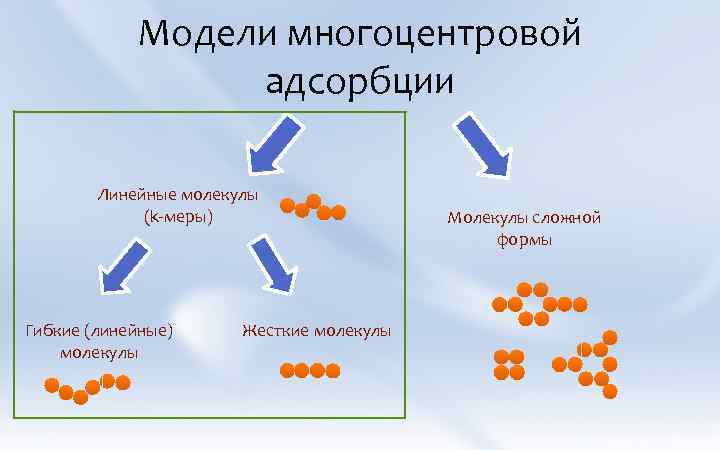
Модели многоцентровой адсорбции Линейные молекулы (k-меры) Гибкие (линейные) молекулы Жесткие молекулы Молекулы сложной формы
Гамильтониан ω – энергия латеральных взаимодействий между двумя ближайшими адсорбированными сегментами молекулы, принадлежащими разным молекулам; μ – химический потенциал; U 0 – энергия взаимодействия между сегментом k-мера и активным центром адсорбции; ci – переменная заполнения; N – число k-меров; k – число сегментов в k-мере.
Латеральные взаимодействия Упорядоченные структуры гомоядерных димеров: a) структура с(4 х2) b) зигзагообразная структура.
Латеральные взаимодействия Отдельный интерес представляет многоцентровая адсорбция гетероядерных и k-меров. Такие системы могут предсказывать поведение на поверхности молекул с разными функциональными группами. В рамках МРГ подразумевается, что латеральные взаимодействия и энергия связи с поверхностью у разных сегментов таких молекул будут различаться. Упорядоченные структуры гетероядерных димеров
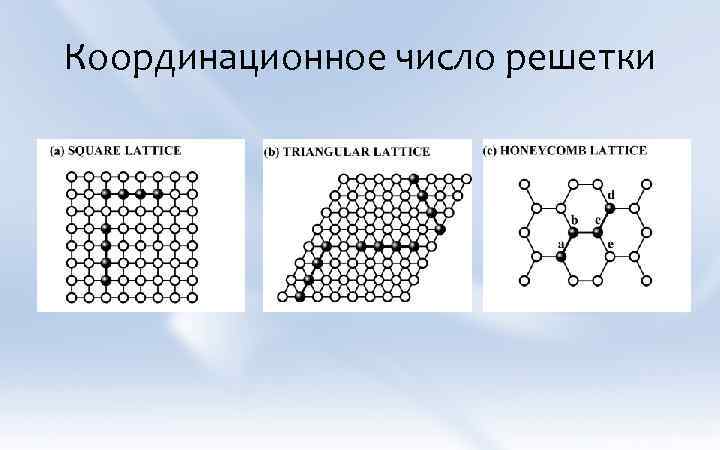
Координационное число решетки
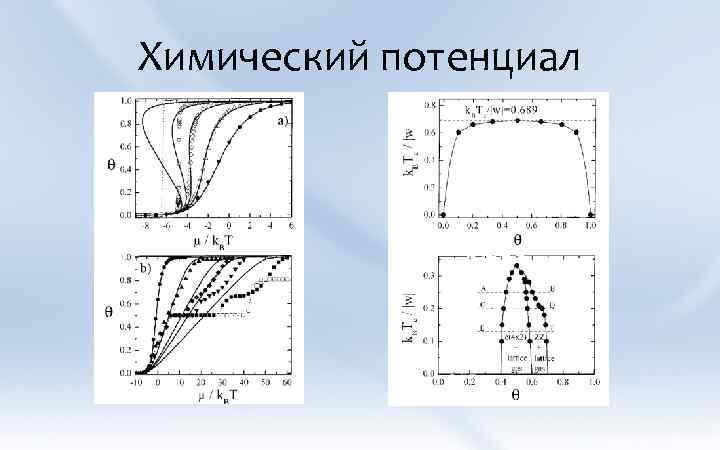
Химический потенциал
Гетерогенность поверхности e) a. b. c. d. e. Шахматные «заплатки» ; Случайные «заплатки» ; Регулярные полосы; Случайная гетерогенность.
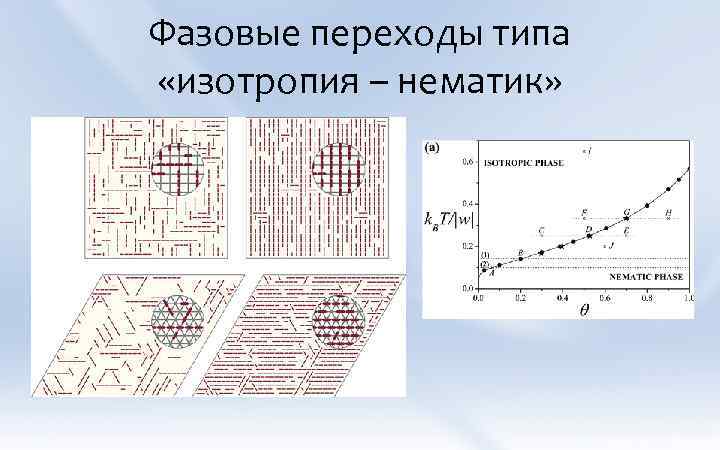
Фазовые переходы типа «изотропия – нематик»
Исследования перколяционных порогов Информация о переходах «перколированная область» - «неперколированная область» на поверхности представляет большой интерес как с точки зрения науки о фазовых переходах, так и с прикладной точки зрения, в частности возникновение поверхностной проводимости. В случае двумерной МРГ перколяционным порогом называется такое минимальное значение функции степени покрытия, что на поверхности бесконечного размера образуется бесконечно большой кластер из адсорбированных молекул. Помимо размерности системы и координационного числа решетки на порог перколяции оказывает значительное влияние размер k-мера.
Скачать презентацию Моделирование процессов на поверхности Многоцентровая адсорбция Многоцентровая
Моделирование процессов на поверхности.pptx