МОДЕЛИРОВАНИЕ ОБОГАТИТЕЛЬНЫХ ПРОЦЕССОВ Вашлаев Антон Иванович ст преп

МОДЕЛИРОВАНИЕ ОБОГАТИТЕЛЬНЫХ ПРОЦЕССОВ Вашлаев Антон Иванович ст. преп. кафедры ОПИ 1

Литература по дисциплине: 1. Тихонов О. Н. Закономерности эффективного разделения минералов в процессах обогащения полезных ископаемых. М. : Недра, 1984. – 208 с. 2. Моделирование обогатительных процессов: Рабочая программа, методические указания, задания для контрольной работы для студентов заочной формы обучения / Сост. В. И. Брагин; ГАЦМи. З. Красноярск, 1999 20 с. 3. Моделирование обогатительных процессов: Методические указания к практическим занятиям / Сост. Ю. М. Емельяшин; КИЦМ. – Красноярск, 1993. – 32 с. 4. Цыпин Е. Ф. , Морозов Ю. П. , Козин В. З. Моделирование обогатительных процессов и схем: Учебник. – Екатеринбург: Издательство Уральского университета, 1996. – 368 с. 5. Справочник по проектированию рудных обогатительных фабрик. / Под ред. О. Н. Тихонова. Книга 1. М. : Недра, 1988. – 374 с. 2

Раздел 1 ОСНОВЫ ТЕОРИИ ОБОГАТИТЕЛЬНЫХ ПРОЦЕССОВ Тема 1 Общие представления о моделировании 3

Цели и задачи моделирования • • • Моделирование – метод изучения объектов, при котором сам объект заменяется его моделью. Модель – аналог объекта, системы или процесса в неко торой форме, отличной от формы их реального существования. Цели – углубленное изучения механизма какого либо явления; прогноз поведения объекта; определения состояния, параметров, режимов системы; оптимизации процесса, аппарата, схемы. 4

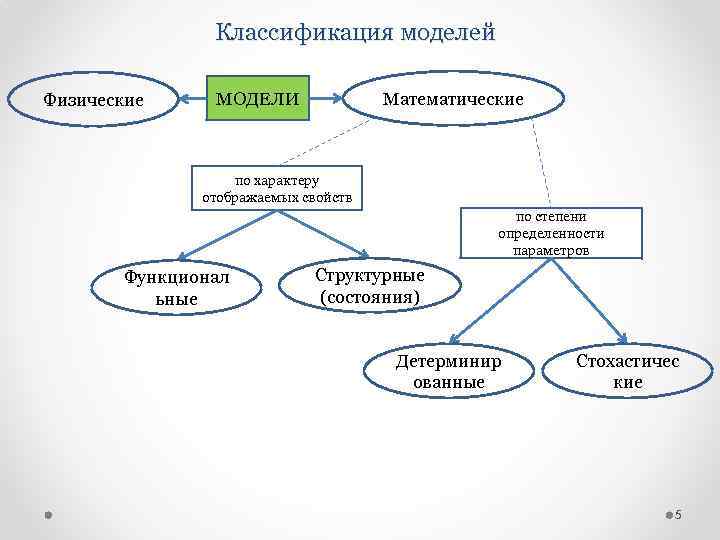
Классификация моделей Физические Математические МОДЕЛИ по характеру отображаемых свойств по степени определенности параметров Функционал ьные Структурные (состояния) Детерминир ованные Стохастичес кие 5

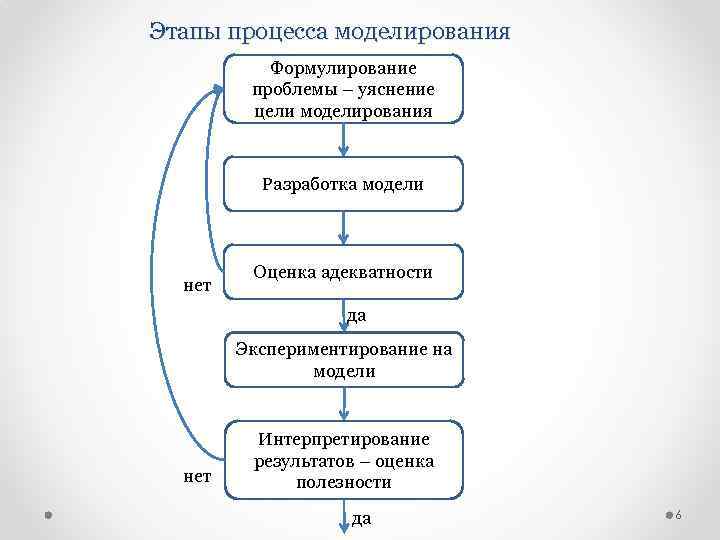
Этапы процесса моделирования Формулирование проблемы – уяснение цели моделирования Разработка модели нет Оценка адекватности да Экспериментирование на модели нет Интерпретирование результатов – оценка полезности да 6

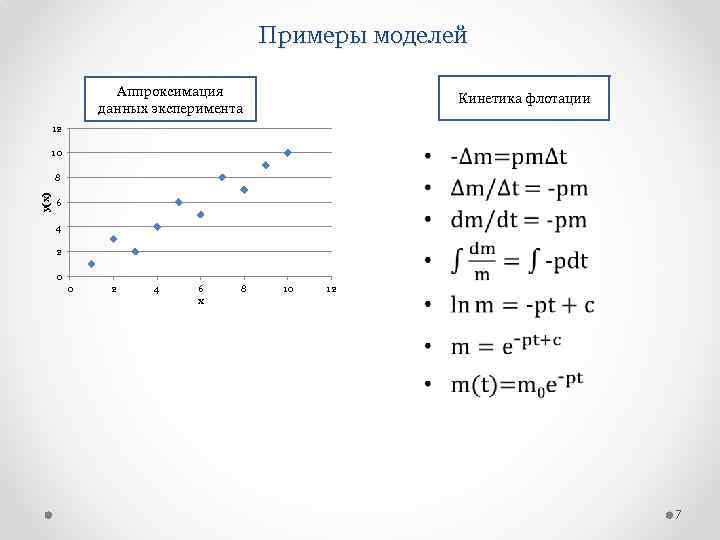
Примеры моделей Аппроксимация данных эксперимента Кинетика флотации 12 • 10 y(x) 8 6 4 2 0 0 2 4 6 x 8 10 12 7

Раздел 1 ОСНОВЫ ТЕОРИИ ОБОГАТИТЕЛЬНЫХ ПРОЦЕССОВ Тема 2 Структура теории моделирования обогатительных процессов 8

Некоторые отличия от общепринятой теории Рудоподготовка – процессы подготовки минеральной смеси к сепарации. Сепарация – процессы разделения минеральной смеси на продукты. Рудоподготовка • Дробление • Измельчение • Реагентная обработка • Обжиг Сепарация • • • Грохочение Классификация Гравитация Флотация Магнитное обогащение • Радиометрия • Электрическая сепарация 9

Характеристики минеральных частиц: признак разделения Признаком разделения ξ называют свойство минеральных частиц, по которому производится сепарация (разделение) в данном процессе. Процесс Свойство • Грохочение l – крупность, мм • Классификация l – крупность, мм • Гравитация ρ – плотность, г/см 3 • Флотация k – флотируемость, м/с • Магнитное обогащение χ– магнитная воспр-ть, см 3/г • Радиометрия φ – светимость • Электрическая сепарация q – удел. эл. заряд, Кл/см 3 10

Характеристики минеральных частиц: диапазон, узкая фракция, элементарная фракция Минеральные частицы в смеси имеют значения признака разделения, находящиеся в интервале от минимального ξ min до максимального ξ max. Другими словами, физическое свойство ξ изменяется в диапазоне ξ min < ξ< ξ max. Этот интервал (диапазон) можно разбить на узкие фракции Δ ξ i, в которых значения признака разделения частиц различаются незначительно и находится в пределах от ξ i до ξ i+1. Δ ξ i ξ min ξ i+1 ξ max ξ dξ ξ min ξ max ξ 11

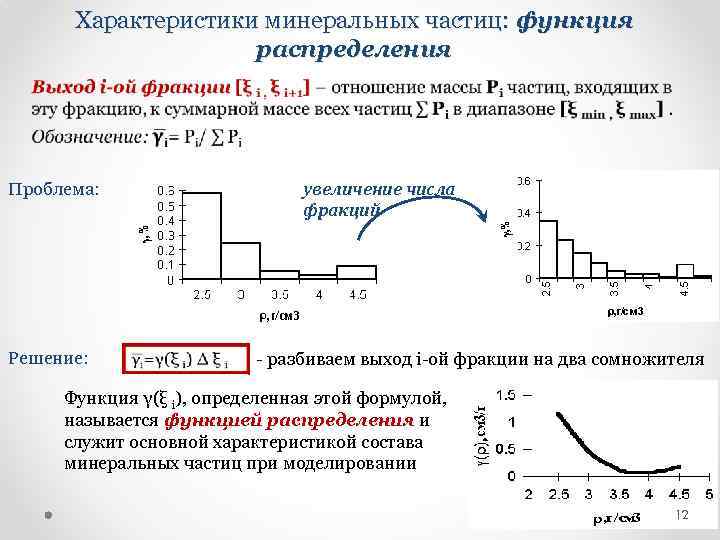
Характеристики минеральных частиц: функция распределения • увеличение числа фракций Проблема: Решение: разбиваем выход i ой фракции на два сомножителя Функция γ(ξ i), определенная этой формулой, называется функцией распределения и служит основной характеристикой состава минеральных частиц при моделировании 12

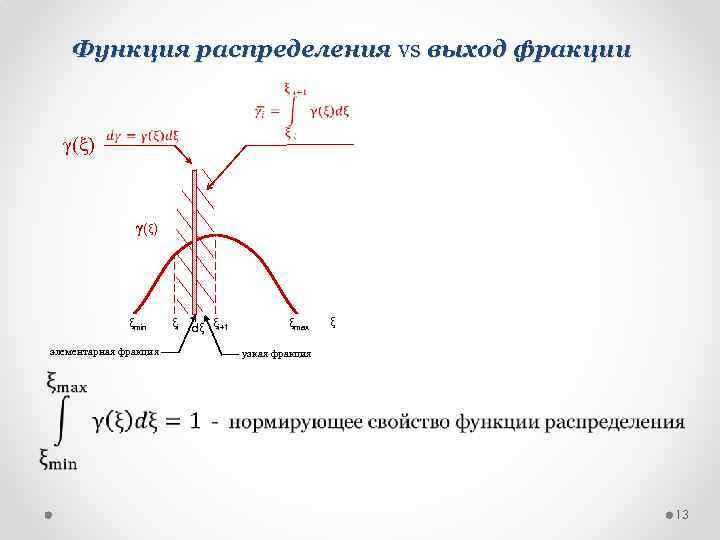
Функция распределения vs выход фракции γ(ξ) γ (ξ ) ξmin элементарная фракция ξi dξ ξi+1 ξmax ξ узкая фракция 13

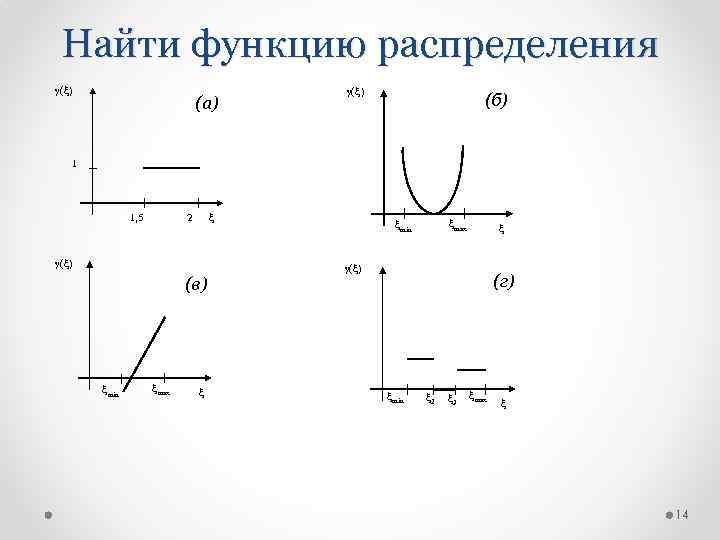
Найти функцию распределения g(x) (а) g(x) (б) 1 x 2 1, 5 g(x) (в) xmin xmax xmin x g(x) (г) xmin x 2 x 3 xmax x 14

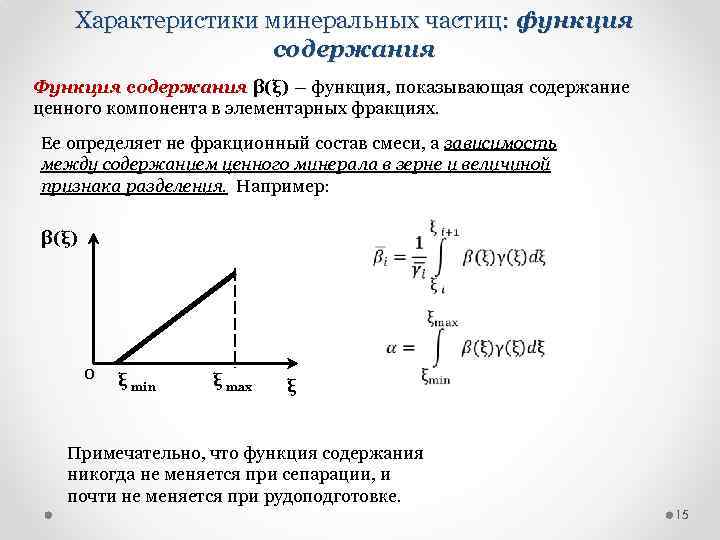
Характеристики минеральных частиц: функция содержания Функция содержания β(ξ) – функция, показывающая содержание ценного компонента в элементарных фракциях. Ее определяет не фракционный состав смеси, а зависимость между содержанием ценного минерала в зерне и величиной признака разделения. Например: β(ξ) 0 ξ min ξ max ξ Примечательно, что функция содержания никогда не меняется при сепарации, и почти не меняется при рудоподготовке. 15

Расчет фракционного состава угля Границы фракции Масса Границы фракции P , кг 3 ρi, т/м фракции Pi, i ρi, т/м 3 кг 1. 1 1. 4 0. 8 Функция Содержание распр ния, золы γ(ρi) золы 10 γ(ρi) 1. 1 1. 4 0. 8 0, 4 10 1, 33 1. 4 1. 7 0. 4 0, 2 30 0, 67 1, 7 2 0. 3 0, 15 50 0, 5 2 2, 3 0. 3 0, 15 70 0, 5 2. 3 2. 6 0. 2 0, 1 90 0, 33 1. 4 1. 7 1, 7 2 2 2, 3 2. 6 0. 4 0. 3 0. 2 30 50 70 90 16

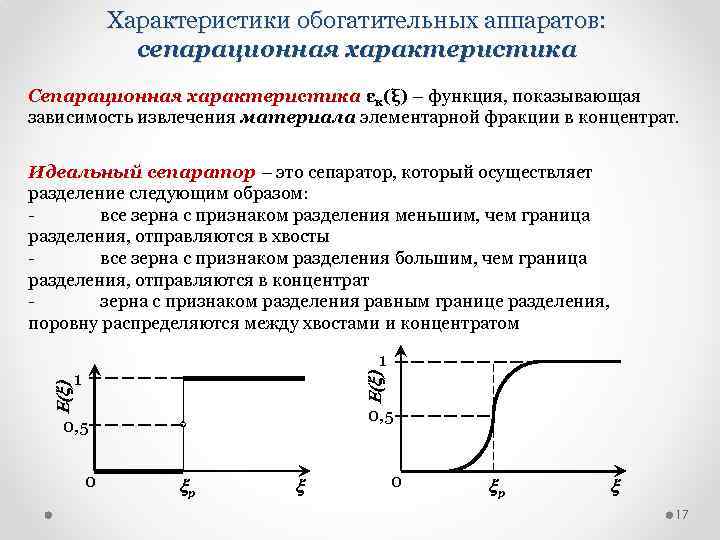
Характеристики обогатительных аппаратов: сепарационная характеристика Сепарационная характеристика εк(ξ) – функция, показывающая зависимость извлечения материала элементарной фракции в концентрат. 1 1 E(x) Идеальный сепаратор – это сепаратор, который осуществляет разделение следующим образом: все зерна с признаком разделения меньшим, чем граница разделения, отправляются в хвосты все зерна с признаком разделения большим, чем граница разделения, отправляются в концентрат зерна с признаком разделения равным границе разделения, поровну распределяются между хвостами и концентратом 0, 5 0 xр x 17

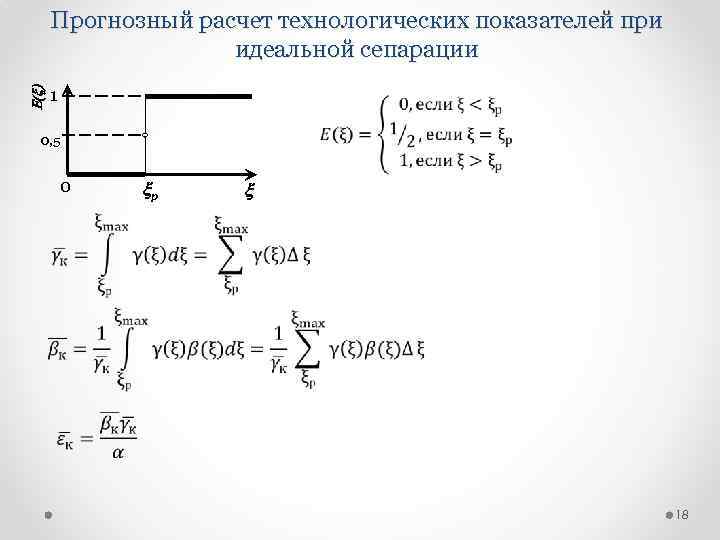
E(x) Прогнозный расчет технологических показателей при идеальной сепарации 1 0, 5 0 xр x 18

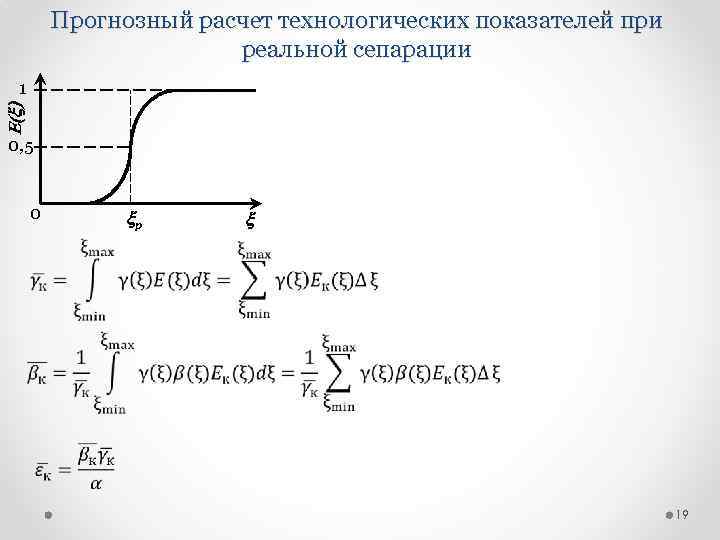
Прогнозный расчет технологических показателей при реальной сепарации E(x) 1 0, 5 0 xр x 19

Экспериментальное снятие сепарационной характеристики Как по известным фракционному составу, функции содержания и сепарационной характеристике можно рассчитать технологические показатели сепарации, так реальна и обратная задача определения сепарационной характеристики Таким образом, для снятия сепарационной характеристики с использованием этой формулы, необходимо провести сепарацию материала известного фракционного состава и определить выход и фракционный состав концентрата 20

Расчет технологических показателей Масса Границы фракции в фракции исходном P , Выход ρi, т/м 3 исходном Pii, Выход ρi, т/м 3 фракции в Содержан кг кг фракции в Содержан исходном ие золы, % 1. 2 1. 4 0. 2 0 1. 2 1. 4 0. 2 0 1. 4 1. 6 1. 8 0. 4 0. 2 0. 4 0. 2 15 15 45 45 1. 8 2. 2 2, 2 3 0. 1 0. 1 65 65 90 90 Сепараци Выход онная фракции в характери концентра стика те 0. 97 0. 6 0. 368 0. 4 0. 152 0. 018 0. 03 0. 006 0. 456 21

Раздел 1 ОСНОВЫ ТЕОРИИ ОБОГАТИТЕЛЬНЫХ ПРОЦЕССОВ Тема 3 Деформации функций распределения и содержания при рудоподготовке (дроблении, измельчении) 22

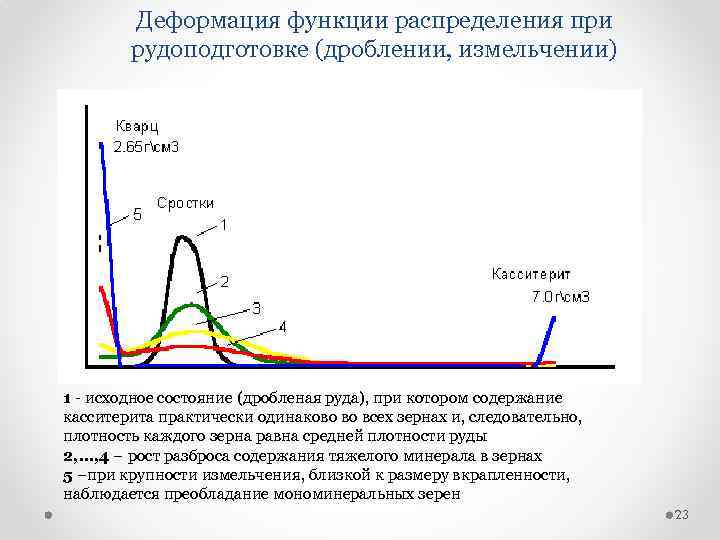
Деформация функции распределения при рудоподготовке (дроблении, измельчении) 1 исходное состояние (дробленая руда), при котором содержание касситерита практически одинаково во всех зернах и, следовательно, плотность каждого зерна равна средней плотности руды 2, …, 4 – рост разброса содержания тяжелого минерала в зернах 5 –при крупности измельчения, близкой к размеру вкрапленности, наблюдается преобладание мономинеральных зерен 23

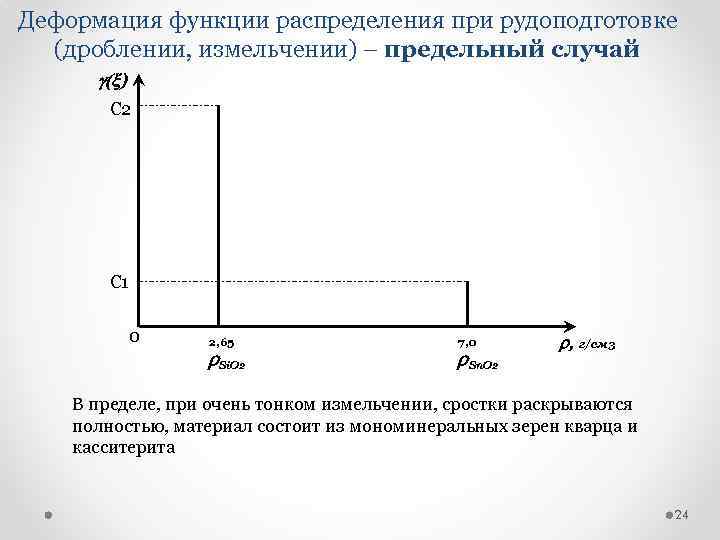
Деформация функции распределения при рудоподготовке (дроблении, измельчении) – предельный случай g(x) С 2 С 1 0 2, 65 r. Si. O 2 7, 0 r. Sn. O 2 r, г/см 3 В пределе, при очень тонком измельчении, сростки раскрываются полностью, материал состоит из мономинеральных зерен кварца и касситерита 24

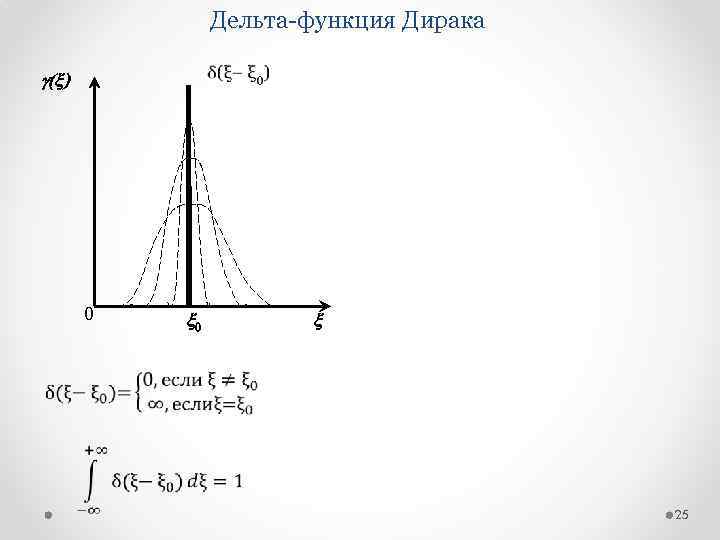
Дельта функция Дирака g(x) 0 x 25

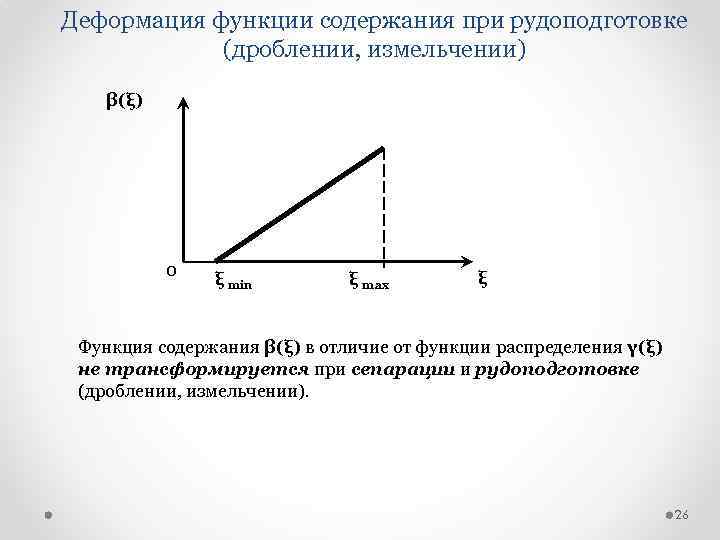
Деформация функции содержания при рудоподготовке (дроблении, измельчении) β(ξ) 0 ξ min ξ max ξ Функция содержания β(ξ) в отличие от функции распределения γ(ξ) не трансформируется при сепарации и рудоподготовке (дроблении, измельчении). 26

Раздел 1 ОСНОВЫ ТЕОРИИ ОБОГАТИТЕЛЬНЫХ ПРОЦЕССОВ Тема 3 Модели сепарационных характеристик 27

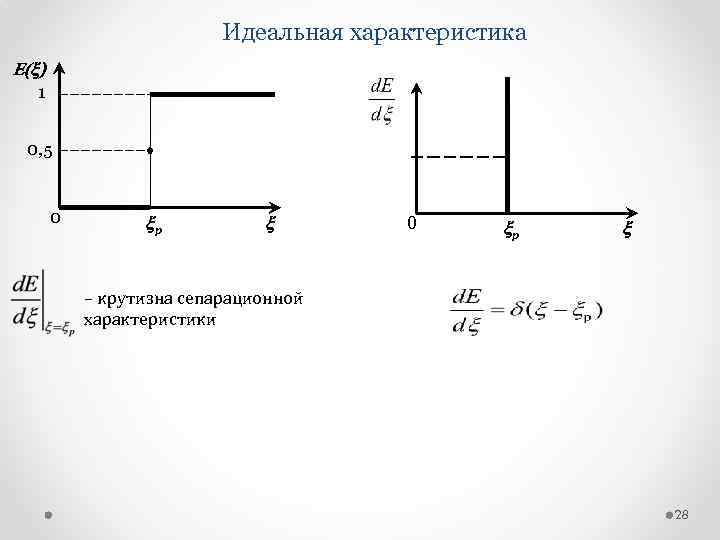
Идеальная характеристика E(x) 1 0, 5 0 xр x – крутизна сепарационной характеристики 28

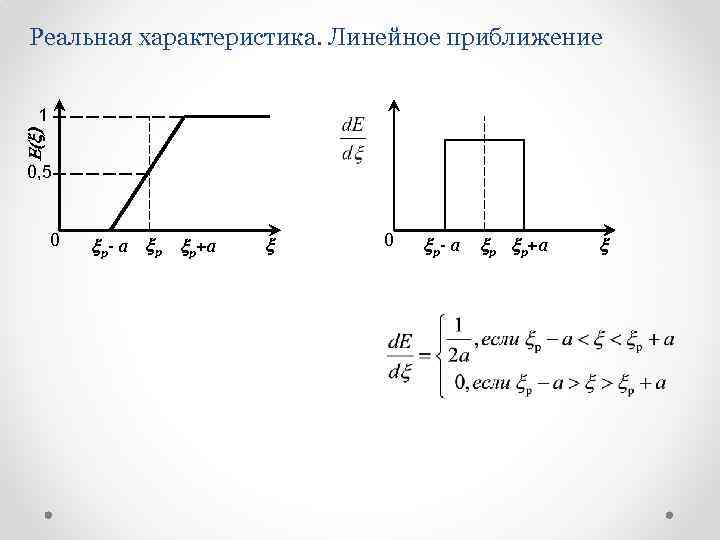
Реальная характеристика. Линейное приближение E(x) 1 0, 5 0 xр- а xр xр+а x

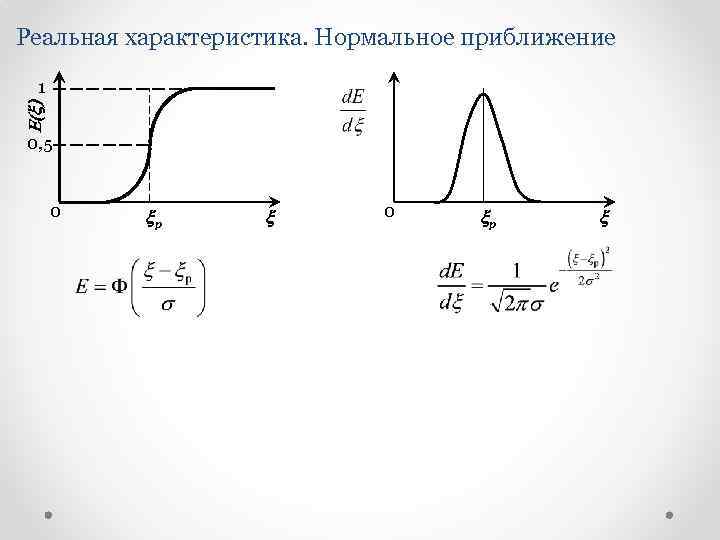
Реальная характеристика. Нормальное приближение E(x) 1 0, 5 0 xр x

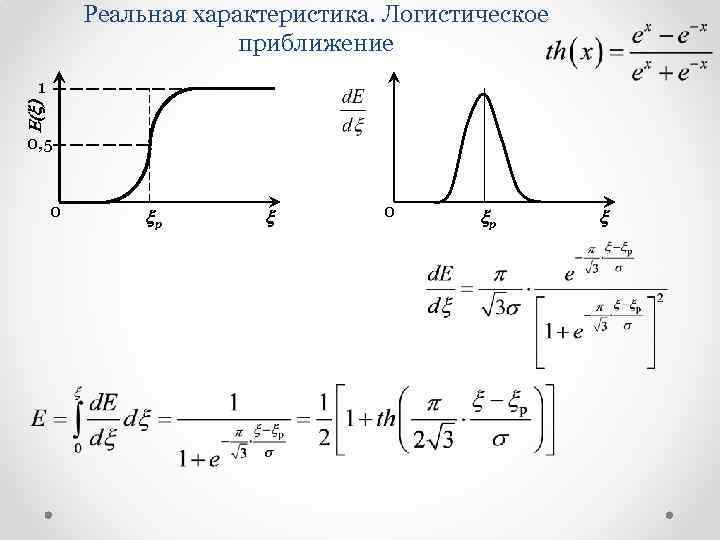
Реальная характеристика. Логистическое приближение E(x) 1 0, 5 0 xр x

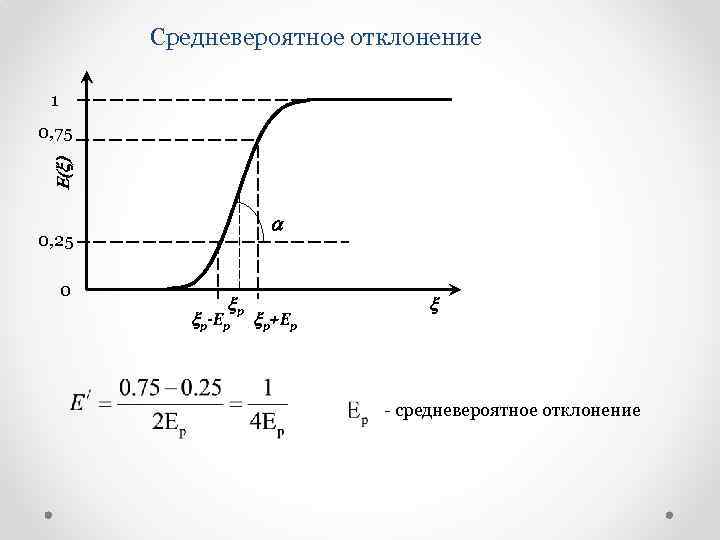
Средневероятное отклонение 1 E(x) 0, 75 a 0, 25 0 xр xр-Ep xр+Ep x средневероятное отклонение

Раздел 2 МОДЕЛИ СЕПАРАЦИОННЫХ ПРОЦЕССОВ Тема 4 Силы, действующие в рабочей зоне сепаратора 33

Основные понятия Рабочая зона аппарата – область, в которой минеральная смесь подвергается воздействию сепарирующих сил, приводящему к пространственному разделению их на область концентрата и область хвостов. В точке (x, y, z) в момент времени t минеральная смесь имеет фракционный состав γ (ξ, x, y, z, t) – функция фракционного состава минерального материала в смеси. V (ξ, x, y, z, t) – скорость движения минеральных частиц в локальной точке зоны (x, y, z, t). 34

Базисные уравнения массопереноса 1. Закон сохранения фракций в локальной точке зоны (Смысл: накопление материала в момент времени t в произвольном объеме равно входящему через границу этого объема материалу минус выходящему через границу материалу. ) dz dy dx 2. Уравнение баланса сил. (Смысл: сумма сил, действующих на минеральные частицы в зоне аппарата равна нулю. ) 35

Классификация сил, действующих на минеральные частицы I. По традиционности выделения: 1. традиционные (детерминированные) 2. среднестатистические (стохастические) – возникают при стесненном движении частиц в аппаратах. m(x, y, z, t) – концентрация минеральной смеси. II. С точки зрения целей сепарации: 1. помогающие сепарации: а) активные гравитационная, вязкого трения, динамического сопротивления, магнитная, электростатическая и т. д. б) реактивные архимедова, типа архимедовой (стохастическая архимедова) 2. вредящие сепарации (антисепарационные): а) градиентная (диффузионная) б) силы сопротивления движению минеральных частиц. 36

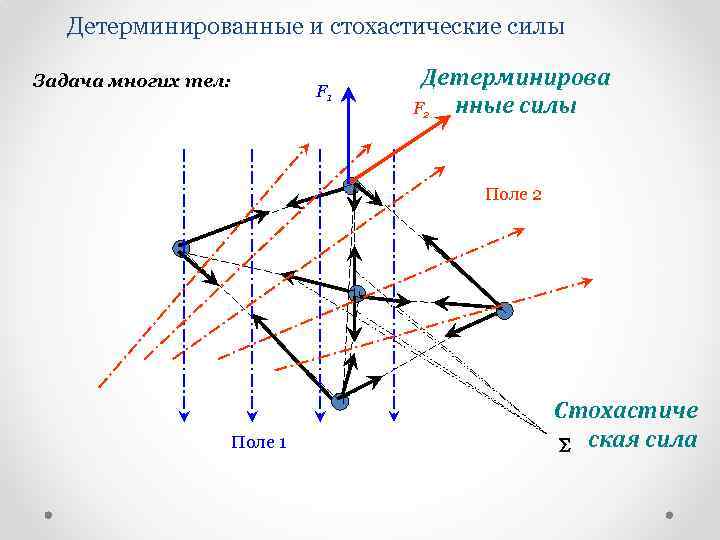
Детерминированные и стохастические силы Задача многих тел: F 1 Детерминирова F 2 нные силы Поле 2 Поле 1 Стохастиче S ская сила

Детерминированные силы Детерминированная сила – взаимодействие частицы и поля гравитационная F 1 F 3 инерции архимедова сопротивления среды (Стокса) магнитная электрическая F 2 Динамичес кое уравнение модели Детерминированная сила лишена случайной составляющей и может быть определена для отдельной частицы

Стохастические силы Стохастическая сила – это усредненное взаимодействие частицы и коллектива частиц Процесс Сила Диссипация энергии Стохастическая сила сопротивления Увеличение энтропии Диффузионная (градиентная) Минимизация энергии системы Конкурентная (стохастическая Архимедова сила)

Стохастическая сила сопротивления

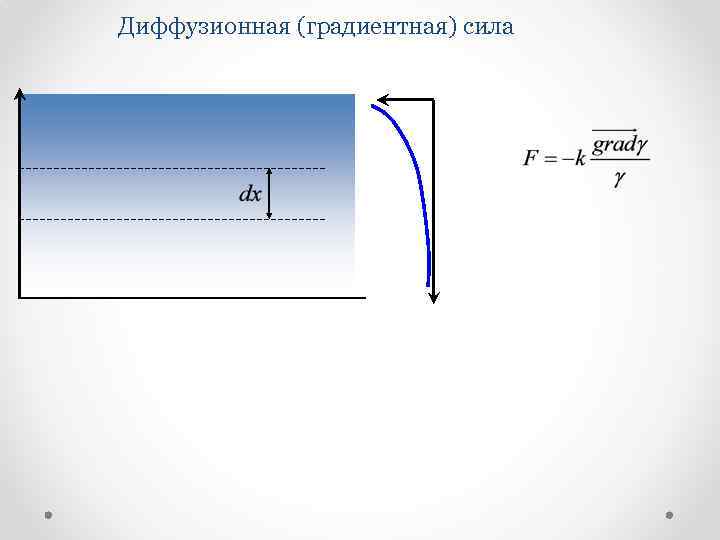
Диффузионная (градиентная) сила

Стохастическая сила Архимеда Однородная среда Fa Общий случай Гравитационное поле Центробежное поле Магнитное поле a Гравитационное или центробежное поле Магнитное поле

Динамическое уравнение массопереноса Выталкивающа я сила Архимеда Сила тяжести Градиентная сила Стохастическая выталкивающая сила Сила сопротивления решение уравнения сепарации

Система уравнений массопереноса Составление уравнений сепарации в рабочих зонах включает объединение уравнений закона сохранения фракций и баланса сил, специфичных для различных обогатительных аппаратов. Рассмотрим пример отсадочной машины с естественной постелью для одномерного случая при сепарации в направлении х. 44

Система уравнений массопереноса 45

Система уравнений массопереноса Выразим vx из второго уравнения - локальное уравнение сепарационного массопереноса 46

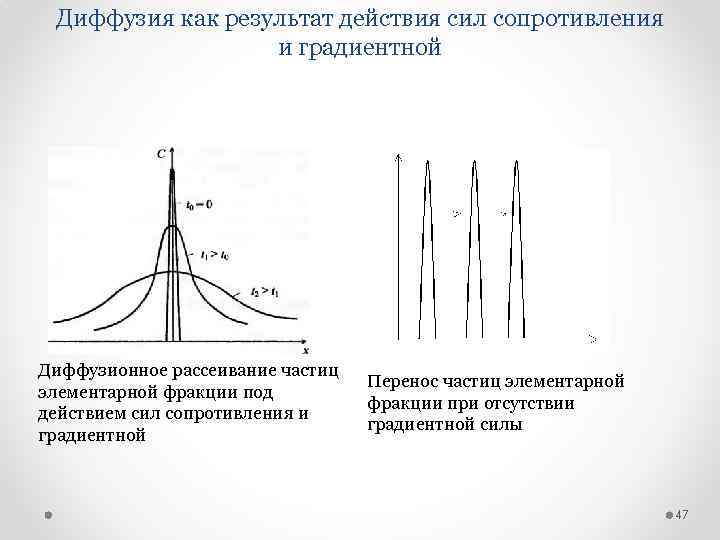
Диффузия как результат действия сил сопротивления и градиентной Диффузионное рассеивание частиц элементарной фракции под действием сил сопротивления и градиентной Перенос частиц элементарной фракции при отсутствии градиентной силы 47

Модели флотации Два главных субпроцесса флотации: минерализация пузырьков и гравитационная сепарация. 48

Периодическая флотация 49

Непрерывная флотация в машинах малой глубины Процесс флотации в этом случае рассматривается как последовательность периодических процессов. Найдите границу разделения kр сепарационной характеристики флотомашины 50

Колонная флотация Крайняя неидеальность сепарационных характеристик неглубоких флотомашин вынуждает использовать развитые схемы флотации, а также искать способы деформации сепарационных характеристик в сторону большей идеальности. Этого можно достичь применением глубоких флотомашин и использованием процессов, происходящих в пенном слое. В неглубоких машинах время подъема пузырька в пену настолько мало, что вероятность разрушения флотокомплекса практически не сказывается на показателях обогащения. При увеличении глубины возникает ситуация, когда вероятно многократное образование и разрушение флотокомплекса на одном пузырьке. Т. е. в одной машине как бы осуществляются перечистки. Флотация в колонных аппаратах позволяет увеличить крутизну сепарационной характеристики и обойтись без использования развитых схем, что и наблюдается на практике. 51

Методика флотометрического анализа 1. Пробу руды флотируют с дробным снятием пены через промежутки времени t 1, t 2, …, tn, что равносильно изменению границы разделения kр в операциях. 52

Методика флотометрического анализа 53