Введение в теорию графов Л.1.ppt
- Количество слайдов: 51

Моделирование и оптимизация систем сетевой структуры Глеб Владимирович Попков e mail popkov@rav. sscc. ru Лекция 1 Основные понятия теории графов

Графом называется пара (V, E), где V - непустое множество элементов, называемых вершинами графа, а E - множество двухэлементных подмножеств V, называемых ребрами графа. Если V={v 1, v 2, …vn}, то множество ребер E={e 1, e 2, …em} задается отображением E V V. Элементы множества Е обозначаются как ек=(vi, vj). Множества вершин и ребер графа G обозначают V(G) и Е(G) соответственно. Число вершин и ребер в графе обозначаются через |V(G)| и |E(G)|. Если |V(G)|=n и |E(G)|=m, то говорят об (n, m)-графе. Две вершины называются смежными, если между ними есть ребро. Ребро называется инцидентным вершине, если вершина является его началом или концом.
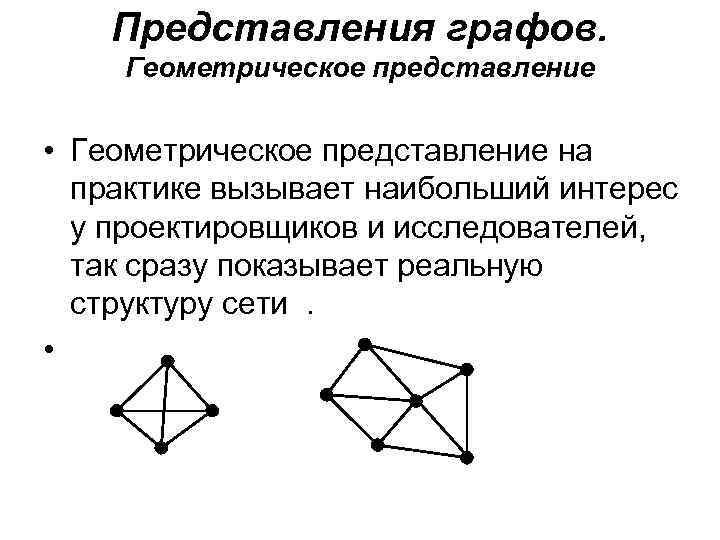
Представления графов. Геометрическое представление • Геометрическое представление на практике вызывает наибольший интерес у проектировщиков и исследователей, так сразу показывает реальную структуру сети. •

Матричные представления • Если элемент прямоугольной матрицы M(G) а(x, е) = 1, тогда и только тогда когда вершина х инцидентна ребру е и равна нулю в противном случае, то она называется матрицей инциденций графа G. • Квадратная матрица N(G) называется матрицей смежности, если элемент этой матрицы b(х, у)=1 тогда и только тогда, когда вершина х смежна с вершиной у и b(х, у)=0, в противном случае.

Степенью вершины называется число инцидентных ей ребер. Степень вершины v обозначается через deg v. Очевидно, что сумма степеней всех вершин графа - четное число, равное удвоенному числу ребер: deg v=2|E(G)|. v VG Ребро называется ориентированным, если у него определены начало и конец, при этом направление ребра помечается стрелкой. Иначе ребро называется неориентированным. Граф H называется объединением графов F и G, если V(H)=V(F) V(G) и E(H)=E(F) E(G). В этом случае пишут H=F G. Граф G называется стягиваемым к графу H, если H получается из G в результате некоторой последовательности стягиваний ребер

Подграфом называется граф, который получается при удалении из исходного графа вершин или ребер. (G 1 =(V 1, E 1), V 1 V, E 1 E) Суграфом называется граф, полученный из исходного удалением ребер с сохранением исходного множества вершин. Частью графа G называется подграф его суграфа. Реберным графом L(G) графа G называется граф, вершинами которого являются ребра графа G, и две вершины графа L(G) смежны тогда и только тогда, когда смежны соответствующие им ребра графа Для произвольного графа G возможно определить понятие дополнительного графа (или дополнения) Ġ следующим образом: V(Ġ)=V(G), и любые две несовпадающие вершины смежны в Ġ тогда и только тогда, когда они не смежны в G.

Операции над графами 1. 2. 3. 4. 5. 6. Удаление вершины из графа. Пусть v вершина графа G. Граф Gv=G v получается из графа G в результате удаления вершины v и всех инцидентных ей ребер. Добавление вершины в граф. Удаление ребра из графа. Пусть e - ребро графа G. Граф Gе=G е получается из графа G в результате удаления ребра e (вершины ребра не удаляются). Добавление ребра в граф. Если вершины u и v графа G не смежны, то можно определить граф G+e, где е=(u, v). Отождествление (или слияние) вершин в графе. Пусть u и v – две вершины графа G. Удалим их вместе с инцидентными им ребрами и добавим новую вершину w, соединив ее ребрами с каждой из вершин, смежных вершинам u и v в графе G. Говорят, что построенный граф получается из графа G отождествлением вершин u и v. Стягивание ребра в графе. Стягивание ребра е=(u, v) означает отождествление смежных вершин u и v. При этом вместо вершин u и v появляется новая вершина, смежная с каждой из вершин, смежных вершинам u и v.

Классы графов. 1. Ориентированный граф – содержит только ориентированные ребра. Множество Е={ek | ek=(v ; vj)} в i этом случае состоит из упорядоченных пар элементов множества V, при этом первая вершина называется началом ребра, а вторая концом. 2. Неориентированный граф – содержит только неориентированные ребра. 3. Смешанный граф – содержит и ориентированные и неориентированные ребра. 4. Мультиграф – содержит мультиребра. 5. Псевдограф – содержит петли. 6. Взвешенный граф (сеть)– если вершинам или ребрам приписаны веса (числовые характеристики). Вес вершины обозначается w(v), вес ребра - w(e).

Типы графов 1. Пустой граф – не содержит ни одного ребра (m=0) 2. Полный граф – каждая пара вершин связана ребром (m=n (n 1)/2) и обозначается Kp. 3. Планарный граф – если граф можно разложить на плоскости без пересечения ребер (m<=3 n 6) , плоский граф – если граф уже изображен на плоскости без пересечения ребер. 4. Дерево – граф, имеющий n вершин и n 1 ребер. 5. Регулярный граф – граф, у которого степени всех вершин равны. 6. Двудольный граф – граф, множество вершин которого можно разбить на два подмножества V 1 и V 2 так, что каждое ребро имеет один конец в V 1, а другой в V 2. Двудольный граф G c такими подмножествами V 1 и V 2 обозначается как G(V 1, V 2, E).

Маршруты, цепи, циклы, пути. 1. Чередующаяся последовательность v 1, e 1, v 2, e 2, …el, vl+1 такая, что ei=(vi, vi+1) называется маршрутом, соединяющим вершины vl и v l+1. Маршрут можно также задать последовательностью вершин или ребер. 2. Маршрут называется: замкнутым, если его конечные вершины совпадают; цепью, если все его вершины различны и простой цепью если все его ребра различны. 3. Граф G называется связным, если любая пара вершин графа соединима маршрутом. 4. Цепь называется циклом, если различны все ее вершины, за исключением концевых. 5. Простая цепь называется простым циклом. если различны все ее ребра и вершины, за исключением концевых. 6. Число ребер l в пути называется его длиной. Число ребер в цикле называется длиной цикла. 7. Цикл называется Эйлеровым, если он содержит все ребра графа. 8. Цикл называется Гамильтоновым, если он содержит все вершины графа.

Поиск кратчайших цепей Алгоритм Дейкстры поиска дерева кратчайших путей. • • • Шаг 1. Для нахождения кратчайших путей в графе от заданной вершины x 0 до всех остальных вершин сначала вес каждой вершины, кроме вершины x 0, принять равным ∞. Вес вершины x 0 равняется нулю. Эта вершина сразу включается в дерево кратчайших путей. Шаг 2. Из вершины x 0 найти смежные с ней вершины графа и их вес принять равным длине соответствующего ребра (x 0, xi). Каждой из таких смежных вершин присвоить пару чисел. Первое из них – номер вершины, от которой пришли; второе – длина пройденного пути по графовой модели. Начиная с третьего шага, эта длина пройденного пути есть сумма вес вершины, от которой пришли плюс длина ребра, по которому шли. Вершина, снабженная парой чисел, называется просмотренной. Шаг 3. Из всех просмотренных вершин графа выбрать вершину с минимальным весом. Ее отметить и включить в дерево кратчайших путей по ребру, по которому вершина получила минимальный вес. Шаг 4. Рассмотреть вершины, которые еще не включены в дерево кратчайших путей, но смежны с последней включенной в дерево вершиной. Для них определяются пары чисел. При необходимости внести в изменения в те пары чисел, где вес в результате этого изменения станет меньше. Шаги 3 и 4 повторять до тех пор, пока не будут включены в дерево все вершины исходного графа.

Поиск Эйлеровых циклов • Для существования Эйлерова цикла в графе необходимо и достаточно, чтобы число ребер инцидентных любой вершине было четно. • Алгоритм нахождения эйлерова цикла. • Шаг 1. Найти все простые циклы в графе. • Шаг 2. Пронумеровать ребра во всех простых циклах графа номером цикла, причем очередной номер присваивается циклу смежному с уже пронумерованными. • Шаг 3. Исходя от выбранной вершины двигаться всегда по ребру с большим номером до возвращения в исходную вершину.

Задача о коммивояжере • • • Постановка задачи. Надо обойти все вершин графа в точности по одному разу и вернутся в исходную так, чтобы суммарный вес ребер был минимальным Алгоритм «иди в ближайший» . Шаг 1. Выбрать исходную вершину и считать ее текущей вершиной строящегося нового цикла. Шаг 2. Найти ближайшую вершину к текущей вершине относительно длины ребра и сделать ее текущей. Увеличить вес цикла на длину ребра. Шаг 3. Если не все вершины включены в цикл, то шаг 2 повторяется. Если в цикл включены все вершины графа, то запомнить суммарный вес ребер, включенных в цикл. Если вес полученного цикла меньше предыдущего решения, считать его наилучшим. Шаг 4. Если не все вершины графа просмотрены как исходные вершины циклов, то перейти на шаг 1, иначе цикл, имеющий минимальный вес объявляется верхней оценкой для задачи коммивояжера.

Расстояния в графе • • • Расстоянием между вершинами u и v называется число, выражающее длину кратчайшего пути между вершинами u и v, во взвешенном графе G и обозначается d(u, v). Графы, для которых выполняются аксиомы метрики, называются метрическими. Аксиомы метрики (аксиомы Фреше): 1. Аксиома рефлексивности: d(u, v)>=0, d(u, v)=0, если u=v; 2. Аксиома симметричности: d(u, v)= d(v, u); 3. Аксиома транзитивности (неравенство треугольника): d(u, v)+ d(v, w)>= d(u, w).

Матрицей расстояний взвешенного графа G, называется квадратная матрица D размерности (N*N), где N – число вершин в графе. На пересечении i –й строки и j –го столбца матрицы D расположены числа d(i, j). При этом полагается d(i, i)=0. Если между вершинами i и j в графе G не существует пути, то полагается d(i, j)=. Эксцентриситетом вершины v в графе G(V, E) называется максимальное из расстояний от вершины v до остальных вершин графа: e(v)= max{ d(v, j)} , j V

Радиусом графа G=(V, E ) называется минимальный из эксцентриситетов вершин и обозначается Rad(G): Rad(G)= min{e(v)}. v V Диаметром графа G=(V, E) называется максимальный из эксцентриситетов вершин и обозначается Diam(G): Diam(G)= max{e(v)} v V Центрами графа называются такие вершины, у которых эксцентриситет равен радиусу графа. Периферийными вершинами называются те, у которых эксцентриситет равен диаметру графа. Передаточным числом вершины взвешенного графа G называется величина: (v) = w(j)*d(v, j) , где w(j) – вес вершины j, d(v, j) – расстояние. j V Медианой графа G(V, E) называется такая вершина v*, у которой передаточное число минимально: (v*) = min{ (v) }. v V

b-медиана графа • Передаточным числом ( Vb ) подмножества Vb V, где |Vb|=b, называется величина: ( Vb ) = w(vj ) d(Vb, , vj ), vj V где d(Vb, , vj ) – расстояние от v j до ближайшей вершины множества Vb то есть d(Vb, , vj ) = min{d(vi, vj)} vi Vb • b медианой называется такое подмножество вершин V*b V, где | V*b |=b , для которого его передаточное число будет минимальным среди всех подмножеств Vb V, |Vb|=b. ( V*b ) = min { ( Vb )}. Vb V

Приближенный алгоритм нахождения b-медианы. • Случайным образом выбираются b вершин, они образуют начальное множество S, аппроксимирующее b-медианное множество V*b. • Затем проверяется, может ли некоторая вершина vj V/S заменить вершину vi S (как медианная вершина), для чего строится новое множество S’ = (S { vj }) { vi } и сравниваются передаточные числа ( S’) и ( S). • Если ( S’) < ( S), то вершина vi в множестве S замещается вершиной vj , в результате получается новое множество S, которое лучше аппроксимирует b-медианное множество V*b. • Процесс продолжается до тех пор, пока построено множество S*, такое, что ни одну его вершину нельзя будет заместить из множества V/S* и получить при этом множество с меньшим передаточным числом, чем ( S* ). • Множество S* является требуемым приближением b-медианы и объявляется приближенным решением задачи.

Независимые множества • Независимым (или внутренне устойчивым) множеством вершин графа называется такое множество вершин, что никакие две вершины из этого множества не смежны. Иными словами, если множество вершин независимо, то подграф, порожденный этим множеством, пустой. • Максимальным независимым множеством вершин называется такое независимое множество, которое не является собственным подмножеством другого независимого множества. • Наибольшим независимым множеством вершин называется независимое множество наибольшей мощности. • Заметим сразу, что не всякое максимальное независимое множество будет являться наибольшим независимым. • Представляют интерес задачи, связанные с отысканием наибольшего независимого множества вершин в графе. К таким задачам относится известная задача о ферзях.

Задача о мирных ферзях • Требуется так расставить на шахматной доске наибольшее число ферзей, чтобы они не атаковали друга. • Таких ферзей, очевидно, может быть не более восьми, так как никакие два из них не должны находиться на одной вертикали или горизонтали. Рассмотрим граф, вершины которого соответствуют клеткам доски, а ребра - парам клеток, лежащих на одной вертикали, горизонтали или диагонали. Ясно, что требуемой в задаче расстановке ферзей требуется отыскать наибольшее независимое множество в построенном графе. • Числом независимости (числом внутренней устойчивости, неплотностью) графа G называется число вершин наибольшего независимого множества и обозначается 0(G).

Алгоритм построения независимого множества • Опишем простой алгоритм построения независимого множества М такого, что М . (1+deg v)¯¹. v V(G) • Каждый раз в графе выбирается вершина минимальной степени и заносится в множество М. • Затем эта вершина и все смежные с ней удаляются из графа и процесс продолжается. • Множество М, полученное таким способом, иногда принимают в качестве приближенного решения задачи отыскания наибольшего независимого множества в графе.

Доминирующие множества • Доминирующим (или внешне устойчивым) множеством графа G называется такое подмножество V’ V вершин графа, что каждая вершина из VV’ смежна с некоторой вершиной из V’. • Минимальным доминирующим множеством называется такое доминирующее множество, которое не является собственным подмножеством другого доминирующего множества. • Наименьшим доминирующим множеством, называется доминирующее множество, имеющее наименьшую мощность.

Задача об атакующих ферзях • Требуется расставить на шахматной доске наименьшее число ферзей так, чтобы каждая клетка доски была под боем. • Очевидно, что всякой такой расстановке ферзей соответствует наименьшее доминирующее множество в графе. • Ядром графа называется такое его подмножество вершин, которое является как независимым, так и доминирующим множеством. • Несложно показать, что ядра графа - это максимальные независимые множества вершин. С другой стороны, доминирующее множество не обязательно независимо.

Задача размещения РАТС Имеется множество населенных пунктов, связанных телекоммуникационной сетью. В некоторых из них необходимо разместить станции связи так, чтобы расстояние от каждого из населенных пунктов до какой-либо станции не превосходило заданной величины. Размещение следует выполнить так, чтобы обойтись минимальным количеством станций. Если поставить в соответствие населенным пунктам вершины графа, в котором две вершины смежны тогда и только тогда, когда расстояние между соответствующими пунктами не превышает заданной величины, то задача, очевидно, сводится к построению в графе наименьшего доминирующего множества.

Покрытия • Говорят, что вершина и ребро графа покрывают друга, если они инцидентны. Таким образом, ребро e=(vi, vj) покрывает вершины vi и vj, а каждая из этих вершин покрывает ребро e. • Вершинным покрытием графа G=(V, E) называется подмножество вершин V’ V, такое, что каждое ребро из E инцидентно хотя бы одной вершине из V’. • Минимальное покрытие – это покрытие графа G которое не содержит покрытия с меньшим числом вершин. Наименьшее покрытие - это покрытие с наименьшим числом вершин среди всех покрытий графа G. • Числом вершинного покрытия называется число вершин в наименьшем покрытии графа G и обозначается 0(G).

Теорема (связь между покрытиями и независимыми множествами графа). • Множество U вершин графа G является покрытием (наименьшим, минимальным) тогда и только тогда, когда Ū=V(G)U - независимое множество (наибольшее, максимальное). Следовательно, 0(G)+ 0(G)= G. • Доказательство: По определению множество Ū независимо тогда и только тогда, когда в графе нет ребра, оба конца которого содержатся в Ū , т. е. когда хотя бы один из концов каждого ребра принадлежит U. Последнее означает, что U - вершинное покрытие. Поскольку U + Ū = G , то, очевидно, наибольшим Ū соответствуют наименьшие U и наоборот. • Теорема доказана.

Клика Подмножество V’ вершин графа G называется кликой, если любые две входящие в него вершины смежны, т. е. если порожденный подграф G(V’) является полным. Клика называется максимальной, если она не содержится в клике с большим числом вершин, и наибольшей, если число вершин в ней наибольшее среди всех клик. Плотностью (или кликовым числом) графа G называется число вершин в его наибольшей клике и обозначается через (G). Подмножество вершин графа G является кликой тогда и только тогда, когда оно независимо в дополнительном графе G, т. е (G)= 0(G). С помощью этого утверждения и приведенных выше оценок числа 0(G) получаются соответствующие оценки числа (G). Очевидно, что все клики графа, как и все максимальные клики, составляют покрытие множества вершин. Числом кликового покрытия называется наименьшее число клик графа G, покрывающих множество V и обозначается через c(G). Очевидно, что c(G) 0(G) для любого графа G.

Паросочетания • Наибольшим паросочетанием является паросочетание с наибольшим числом ребер среди всех паросочетаний графа G. • Числом паросочетания графа G называется число ребер в наибольшем паросочетании и обозначается через 1(G). Ясно, что независимые множества ребер графа G находятся во взаимно однозначном соответствии с независимыми множествами вершин реберного графа L(G), и, следовательно, 1(G)= 0(L). Тем не менее для нахождения наибольшего паросочетания в произвольном графе существуют эффективные алгоритмы. • С понятием паросочетания тесно связано понятие реберного покрытия. • Максимальным паросочетанием во взвешенном графе называется паросочетание с максимально возможным весом.

Реберное покрытие • Реберным покрытием графа G называется такое подмножество ребер E’ E, которое покрывает все вершины графа, т. е. такое, что каждая вершина в G инцидентна по крайней мере одному ребру из E’. • Реберное покрытие графа называется минимальным, если в нем не содержится покрытий с меньшим числом ребер, и наименьшим, если число ребер в нем наименьшее среди всех покрытий. • Число ребер в наименьшем реберном покрытии графа G называется числом реберного покрытия и обозначается через 1(G). • Очевидно, что 1(G) G /2. • Паросочетание называется совершенным (или 1 фактором), если оно одновременно является реберным покрытием.

Легко видеть, что если в графе есть совершенное паросочетание, то оно является наименьшим реберным покрытием. На слайде 24 показано, что число вершин в наибольшем независимом множестве и число вершин в наименьшем покрытии графа G порядка n связаны соотношением 0(G)+ 0(G)= G =n. Аналогичное верно и для соответствующих реберных параметров, т. е. справедлива следующая Теорема Галлаи. (Т. Галлаи, 1959 г. ). Для любого графа G порядка n без изолированных вершин верно равенство 1(G)+ 1(G)= G =n.

Задача о китайском почтальоне • • • Найти кратчайший путь обхода всех ребер графа с возвращением в исходную вершину. При этом допускается проходить некоторые ребра дважды и заходить в вершины более одного раза. Название этой задачи связано с моделью китайского почтальона – почтальону требуется разнести почту по городу Шанхаю, побывав на каждой улице города, с возвращением в исходный пункт и пройти при этом как можно меньший путь. . Так как граф неэйлеров, то его искусственно сводят к некоторому эйлеровому графу, удваивая некоторые ребра. Если эти ребра выбраны правильно, то пройденный путь можно найти как путь в эйлеровом графе, и он действительно будет наиболее коротким из всех возможных путей, хотя по некоторым ребрам такого графа (удвоенным), искусственно сведенного к эйлерову, приходится пройти дважды. Выбор ребер графа G, которые при решении этой задачи удваиваются, производится с использованием понятия наименьшего совершенного паросочетания.

Алгоритм Хуанг-Туи решения задачи о китайском почтальоне. • • • Шаг 1. Проверить является ли граф эйлеровым или нет. Если граф является эйлеровым, то найти эйлеров цикл по алгоритму Хуанг-Туи (шаг 4). Если граф не является эйлеровым, то на шаг 2. Шаг 2. Построить полный граф на множестве вершин исходного графа G с нечетными степенями. На полном графе проставить веса ребер, равные расстояниям между вершинами в исходном графе. Шаг 3. Найти наименьшее совершенное паросочетание на полном графе по приближенному алгоритму. Упорядочить ребра полного графа по возрастанию их весов. В порядке записи включать в рассмотрение ребра, пока не получиться связанный граф. Попытаться построить совершенное паросочетание. Если это не получается, то добавляют еще ребра из ряда. Шаг 4. Удвоить все ребра этого наименьшего совершенного паросочетания и разметить эти удвоенные ребра на исходном графе. Шаг 5. Рассчитать исходный граф G с некоторыми удвоенными ребрами по алгоритму Хуанг Туи и найти в доработанном таким образом графе эйлеров цикл.

Элементарные свойства и определения деревьев • Деревом называется неориентированный связный граф без циклов. • Неориентированный граф без циклов называется лесом. • Граф называется ациклическим, если в нем нет циклов. • Дерево конечно, если число вершин в нем конечно, и бесконечно в противном случае. Дерево с одной вершиной называется тривиальным, вырожденным или пустым. Число вершин дерева иногда называют порядком дерева. • Корневое дерево – это дерево Tv, в котором выделена некоторая вершина v, называемая корнем. • Деревья обладают рядом свойств, каждое из которых полностью

Теорема (характеризующие свойства деревьев). • • Для графа G следующие утверждения эквивалентны: G – дерево; Любые две вершины в G соединены единственной простой цепью; G – связный граф и p=q+1; G – ациклический граф и p=q+1 G – ациклический граф, и если любую пару несмежных вершин соединить ребром x, то в графе G+x будет точно один простой цикл; G- связный граф, отличный от Kp для p 3, и если любую пару несмежных вершин соединить ребром x, то в графе G+x будет точно один простой цикл; G – граф, отличный от K 3 K 1 и K 3 K 2, p=q+1, и если любую пару несмежных вершин соединить ребром x, то в графе G+x будет один простой цикл.

Минимальное остовное дерево (каркас) графа Алгоритм Прима – Краскала Шаг 1. Упорядочим ребра по убыванию веса. Шаг 2. Удаляем очередное ребро, если граф остается связным. Шаг 2 -й продолжается до тех пор пока не будут просмотрены все ребра.

. Плоские и планарные графы • Плоским графом назовем граф, вершины которого являются • точками плоскости, а ребра – непрерывными плоскими линиями • без самопересечений, соединяющими вершины так, что никакие два ребра • не имеют общих точек, кроме инцидентной им обоим вершины. Любой • граф, изоморфный плоскому графу, будем называть планарным.

Грани плоского графа. Формула Эйлера • Гранью плоского графа будем называть максимальное по включению множество точек плоскости, каждая пара которых может быть • соединена жордановой кривой, не пересекающей ребра графа. • Границей грани будем считать множество вершин и ребер, принадлежащих этой грани. Отметим, что всякий плоский граф имеет одну, и притом единственную, неограниченную грань. Такая грань называется внешней, а остальные грани – внутренними.

Теорема Эйлера. Для всякого связного плоского графа справедливо равенство: p – q + f = 2 Доказательство. • Пусть G – связный плоский p – вершинный граф. Рассмотрим некоторый остов T этого графа. Очевидно, что дерево T имеет одну грань (внешнюю) и p вершин. В то же время известно, что число ребер дерева. Т равно p – 1. Поэтому для графа T формула Эйлера верна. Теперь будем поочередно добавлять к T недостающие ребра графа G. При этом на каждом шаге число вершин, естественно, не меняется, а число ребер и число граней увеличивается на единицу. Следовательно, формула Эйлера будет верна для всякого графа, получающегося в результате таких шагов, а поэтому она верна и для графа G, которым заканчивается вся эта процедура. □

Следствия • Следствие 1. У всякого выпуклого многогранника сума числа вершин p и числа граней f без числа ребер q равна двум: p + f – q = 2. • Следствие 2. Число граней любой плоской укладки связного планарного графа постоянно и равно q – p + 2. • Другими словами, число f является инвариантом планарного графа, т. е. не зависит от способа укладки этого графа на плоскости. • Следствие 3. Для связного планарного (p, q) – графа q 3 p – 6 при p 3. • Отсюда немедленно следует, что графы K 5 и K 3, 3 не планарны. • Очевидно, что не всегда граница грани плоского графа является простым циклом. Однако для двусвязных графов это так.

Критерии планарности • • • Теорема Понтрягина – Куратовского. Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K 5 или K 3, 3. Помимо критерия Понтрягиа – Куратовского есть и другие критерии планарности графа. Приведем некоторые из них без доказательств. Критерий Вагнера. Граф планарен тогда и только тогда, когда в нем нет подграфов, стягиваемых к графам K 5 или K 3, 3. Очевидно, что все ациклические графы планарны. Поэтому вполне естественна формулировка критерия планарности, исключающая этот тривиальный случай. Таким критерием является следующий Критерий Маклейна. Граф планарен тогда и только тогда, когда в каждом его нетривиальном блоке есть такой базис циклов C 1, C 2, …, Ck и такой дополнительный цикл C 0, что любое ребро блока принадлежит ровно двум из этих k+1 циклов.
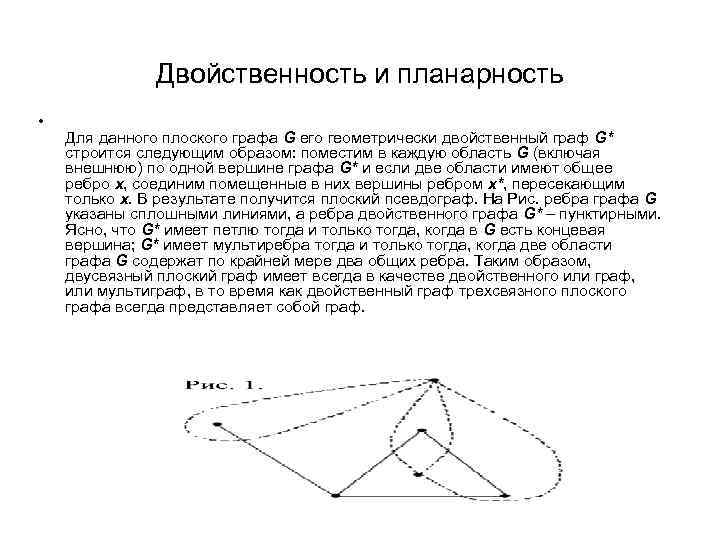
Двойственность и планарность • Для данного плоского графа G его геометрически двойственный граф G* строится следующим образом: поместим в каждую область G (включая внешнюю) по одной вершине графа G* и если две области имеют общее ребро x, соединим помещенные в них вершины ребром x*, пересекающим только x. В результате получится плоский псевдограф. На Рис. ребра графа G указаны сплошными линиями, а ребра двойственного графа G* – пунктирными. Ясно, что G* имеет петлю тогда и только тогда, когда в G есть концевая вершина; G* имеет мультиребра тогда и только тогда, когда две области графа G содержат по крайней мере два общих ребра. Таким образом, двусвязный плоский граф имеет всегда в качестве двойственного или граф, или мультиграф, в то время как двойственный граф трехсвязного плоского графа всегда представляет собой граф.

Критерий Уитни. • Граф планарен тогда и только тогда, когда он комбинаторно двойственный. • Таким образом, можно сформулировать следующий список эквивалентных условий: • G – планарный граф; • в G нет подграфов, гомеоморфных K 5 и K 3, 3; • в G нет подграфов, стягиваемых к K 5 и K 3, 3; • G имеет комбинаторно двойственный граф; • в каждом нетривиальном блоке графа G есть такой базис циклов C 1, C 2, …, Ck и такой дополнительный цикл C 0, что любое ребро блока принадлежит ровно двум из этих k+1 циклов.

Связность графов • Граф G=(X, U) связен, если между любой парой вершин существует соединяющий их маршрут. • Граф G=(X, U) к- связен, если при удалении любых его к-1 вершин, он остается связным. • Две вершины х и у графа G=(X, U) к – связны, если при удалении любых к-1 вершин, кроме х и у, они остаются связными. • (х, у)-цепи независимы, если они не имеют общих вершин, кроме х и у. • Аналогичные определения формулируются для ребер, при этом в соответствующих определениях слово «вершина(ы)» заменяются на «ребро(а)» .

Теоремы Менгера и Оре • Теорема Менгера для вершин. Две вершины х и у к-связны, тогда и только тогда, когда между ними существуют к независимых (х, у)-цепей. • Теорема Менгера для ребер. Две вершины х и у к - реберно-связны, тогда и только тогда, когда между ними существуют к независимых по ребрам (х, у)-цепей. • Теорема Оре. Между вершинами х и у можно увеличить число независимых (х, у)-цепей, если между ними существует секущий чередующейся (х, у) - маршрут.

Метод секущих цепей (Оре) Поиск секущего маршрута • • • Пусть между вершинами х и у существует к-1 независимых цепей. Шаг 1. Ребра независимых цепей отметим. Шаг 2. Если в вершинах х и у существуют не отмеченные ребра, то на шаг 3 иначе на шаг 7. • Шаг 3. Строится возвратный секущий маршрут следующим образом: 3. 1. Выходим из вершины х по не отмеченному ребру и ориентируем его от вершины х. 3. 2. Идем по не отмеченным ребрам (ориентируем их) пока не встретим независимую цепь(ее ребра отмечены) или вершину у, в последнем случае перейдем на шаг 4. 3. 3. Возвращаемся назад к х до те пор пока не встретим вершину с неотмеченным инцидентным ребром и выходим по этому ребру, ориентируем его и повторяется процедура 3. 2. Если такое ребро не встретилось, то возвращаемся назад по возвратному секущему маршруту объявляя ориентированные ребра запретными, пока не встретим другое не отмеченное ребро и пойдем по нему на 3. 1. Если все не отмеченные ребра в процессе построения секущего маршрута станут запретными то на шаг 7.

Метод секущих цепей (Оре) Увеличение числа цепей • Шаг 4. Увеличиваем число независимых цепей следующим образом: 4. 1. Выходим из их по ориентированному ребру и идем по секущему маршруту пока не встретим отмеченные ребра из существующей независимой цепи или вершину у (в этом случае переходим на Шаг 5). 4. 2. Пойдем по ней по направлению вершины у пока не встретим ориентированное ребро секущего маршрута 4. 3. Пойдем по нему пока не встретим отмеченные ребра из существующей независимой цепи, на 4. 2. или вершину у (в этом случае переходим на Шаг 5). • Шаг 5. Переходим на шаг 4. заменяя пункт 4. 1 на следующий. 4. 1* Выходим по отмеченному ребру и далее переходим на 4. 2. Если все цепи исчерпаны, то на шаг. 6 • Шаг 6. Число независимых цепей увеличено на 1. • Шаг 7. Конец. Число независимых цепей увеличить нельзя.

Поток в сети • • • Условие 1. 0 < f(x, y) < c(x, y), (x, y) E. Для любой вершины x (при этом только x s, t) величина выходящего потока должна быть равна величине входящего потока в вершину x. Условие 2. ∑ fx+(e) ∑fx (e)=0 , e Ix+ e Ixˉ где Ix+ - множество ребер инцидентных вершине x по которым поток входит; Ixˉ - множество ребер, по которым поток исходит; Суммарное число единиц потока, выходящих из источника, должно быть равно суммарному числу единиц потока, входящих в сток. Если указанное число обозначить через С, то эти условия можно представить следующим образом: Условие 3. ∑ ft+(e) = C , e It+ Условие 4. ∑fs (e)=C. e Isˉ Потоком из s в t в сети G=(V, E) называется набор величин f(x, y), удовлетворяющий всем четырем условиям. И наоборот, если указан набор величин, удовлетворяющий этим четырем условиям, то определен поток из источника s к стоку t.

Понятие разреза. • • (s, t) – (реберным) разрезом в графе называется некоторый набор ребер G при удалении которых из графа источник s и сток t оказываются в разных компонентах связности. Величина разреза определяется суммарным весом ребер (или дуг) входящих в этот разрез. Наименьший разрез (или минимальный) – это разрез имеющий минимально возможную величину. Понятие величины разреза можно проиллюстрировать рисунком Теорема Форда - Фалкерсона. Величина максимального потока из s в t равна величине минимального разреза, отделяющего s от t.

Методы определения максимального потока Метод насыщения ребер • • Шаг 1. Найти в исходном графе независимые пути из вершины s в вершину t. Шаг 2. Рассмотреть последовательно из найденных на шаге 1 путей. В рассмотренном пути найти разрез с минимальной пропускной способность, которые отметить как насыщенные. Остальные ребра на этом пути расщепить (пропускная способность всех ребер получаемых при расщеплении и соединяющих одну и ту же пару вершин в сумме должна быть равна пропускной способности исходного ребра соединяющего эту пару вершин). Шаг 3. Найти последовательно все остальные пути из вершины s в вершину t. Используются ребра полученные при расщеплении. Каждый раз на новом пути отмечать насыщенные ребра и расщеплять все остальные. Шаг 4. Построить все возможные разрезы через насыщенные ребра. Шаг 5. Определить величины всех разрезов (по первоначальным весам входящих в разрезы ребер) Шаг 6. Найти минимальный по величине разрез из всех построенных на шаге 4. Шаг 7. Найти максимальный s t – поток равный по величине минимальному разрезу в графе в соответствии с теоремой Форда-Фалкерсона.

Метод двойственного графа для определения максимального (s-t ) потока на графических моделях сети • Метод двойственного графа можно применять только для плоских графов. Кроме того, его рекомендуется применять, когда вершины s и t находятся на внешних гранях исходного графа. Алгоритм на основе метода двойственного графа не указывает ребра, по которым пройдет максимальный поток. Он дает лишь численную величину этого потока. • Опишем последовательность построения графа двойственного исходному графа G. • Шаг 1. Произвести мысленно линию через вершины s и t. • Мысленно построить через эту прямую плоскость перпендикулярную плоскости чертежа. • Шаг 2. По обеим сторонам плоскости на чистом поле чертежа проставить вершины двойственного графа a и b

Задавайте вопросы
Введение в теорию графов Л.1.ppt