МОДЕЛИРОВАНИЕ ЭЛЕКТРОННОЙ АППАРАТУРЫ Воспроизведение процессов в проектируемых системах

МОДЕЛИРОВАНИЕ ЭЛЕКТРОННОЙ АППАРАТУРЫ Воспроизведение процессов в проектируемых системах с целью обеспечения анализа проектных решений возможно только путем моделирования, т. е. создания тех или иных аналогий интересующих процессов.

2. 1. МЕТОДЫ МОДЕЛИРОВАНИЯ СИСТЕМ ЭЛЕКТРОННОЙ ТЕХНИКИ • Первоначально в качестве моделей использовались реальные системы, близкие к проектируемой по отдельным параметрам и характеристикам (прототипы). • Однако необходимость выбора реальных систем-аналогов в качестве моделей существенно сдерживает разработку систем принципиально нового типа, резко отличающихся по уровням параметров и характеристик.

• Дальнейшее развитие моделирование получило в двух основных направлениях. • Первое – создание электрических (электродинамических) моделей. • Второе – создание аналоговых моделей электрических систем. • Электродинамические, по существу масштабные физические, модели создаются с помощью функциональных элементов и связей, во многом аналогичных реальным системам. В их состав можно включать отдельные реальные элементы, например, регуляторы, датчики, аппараты защиты и т. п. Указанные особенности придают электродинамическим моделям универсальность и многоцелевое назначение. Они обеспечивают не только моделирование и исследование процессов в аналогичных системах, включая проектируемые, но и проведение испытаний и исследований новых элементов и приборов.

• В отличие от физического подобия процессов, присущего электродинамическим моделям, аналоговые модели электрических систем строятся на основе математического подобия интересующих процессов и процессов аналоговых вычислительных машин (АВМ). • Для моделирования необходимо сначала составить математическое описание процессов в реальной или проектируемой системе, а затем набрать и решать задачу на АВМ со стандартным набором элементов.

• К преимуществам аналоговых моделей можно отнести большое быстродействие, возможность решения относительно сложных систем уравнений, легкость варьирования параметров моделируемой системы, удобство наблюдения и регистрации процессов, компактность и т. п. • Аналоговое моделирование сталкивается с трудностями подготовки задачи, связанными с переводом исходной системы уравнений в машинные уравнения, масштабированием коэффициентов, а также невысокой точностью решений. В связи с этим аналоговые модели получили практическое применение для систем небольшой сложности.

• Аналоговые модели интересны с точки зрения присущей им двойственности. • С одной стороны, они обеспечивают только математическое подобие процессов, • С другой – они реализуются в виде физических процессов в элементах АВМ, которые также собираются с помощью электронных компонентов. • Эта двойственность определяет положение аналоговых моделей как переходных от физических моделей к математическим моделям.

• Наиболее эффективными являются гибридные модели, использующие преимущества физических и математических моделей и компенсирующие их недостатки. • В настоящее время гибридные модели на базе электродинамических моделей и ЭВМ получили наиболее широкое применение в виде автоматизированных экспериментальных комплексов. • В этих комплексах обеспечивается физическая аналогия моделируемых процессов, автоматический съем и обработка результатов испытаний, гибкая смена параметров и элементов аппаратурного типа, установка режимов испытаний и т. д. • Область применения автоматизированных экспериментальных комплексов ограничивается в основном всесторонним обследованием опытных образцов систем и их элементов.

• Под математическим моделированием понимают способ исследования путем изучения явлений, имеющих различное физическое содержание, но описываемых одинаковыми математическими соотношениями. • Наиболее универсальным средством математического моделирования являются ЭВМ, позволяющие решать практически любого типа системы уравнений очень высокой сложности. • Дискретный характер переменных и арифметический характер операций в ЭВМ требуют преобразовать уравнения, описывающие непрерывные процессы, в уравнения дискретных аналогов этих процессов. Поэтому моделирование с помощью ЭВМ часто называют цифровым или электронным моделированием.

• Математическая модель позволяет проанализировать предельные режимы работы ЭУ, физическая реализация которых опасна, а также быстро определять статические и динамические характеристики ЭУ и прогнозировать их изменение под воздействием различных возмущающих факторов.

• В общем виде математическая модель технического объекта есть совокупность математических объектов (чисел, переменных, матриц и т. д. ) и отношений между ними (математических схем), которые адекватно отражают свойства технического объекта. • При исследовании любого объекта строится его математическая модель, которая описывает основные закономерности объекта, затем производятся исследования на модели и результаты исследования модели распространяются на исследуемый объект. • В англоязычной литературе для обозначения этих этапов обычно используются два отдельных понятия: mathematical modeling (математическое моделирование) – процесс составления математических описаний и simulation – процесс реализации математического описания с помощью технических средств и процесс исследования на модели.

• На стадии проектирования, особенно в САПР, предпочтение отдается цифровым моделям, исходя из общности технических средств проектирования и моделирования, информационной базы данных на всех этапах проектирования, большого быстродействия и высокой точности расчетов современных ЭВМ, широких возможностей наглядного, графического представления моделируемых процессов. • Таким образом, на современном этапе развития средств САПР при проектировании и исследованиях электронной аппаратуры в процессе продвижения от замысла к готовому изделию применяются следующие виды моделирования.

Моделирование систем: ММ – математическое моделирование; НЭ – натурный эксперимент; ЦВМ – моделирование на цифровых вычислительных машинах; АЦВС – моделирование на аналого-цифровых вычислительных системах; АВМ – моделирование на аналоговых вычислительных машинах; МПА – модели прямой аналогии. Электрические цепи являются моделями прямой аналогии многих физических систем; ФМ – физическое моделирование (масштабные макеты); ПНМ – полунатурное моделирование.

• К основным методам исследования математических моделей относятся: • аналитическое исследование; • имитационное моделирование. • Аналитические (символьные) модели это модели, в которых для представления процесса или системы используются символы. • Аналитическая модель даёт решение в замкнутом виде, после формирования системы уравнений относительно искомых величин, которая допускает получение нужного результата аналитическим методом. • Аналитическое моделирование – теоретическое исследование объекта или его отдельных характеристик, вывод расчётных формул, уравнений и алгоритмов, и реализация их на ЭВМ. • Аналитические модели могут исследоваться численными методами, при этом путем нахождения частных решений определяются характерные особенности объекта и закономерности его функционирования на заданном интервале времени или изменения параметров.

• Исторически первым сложился аналитический подход к исследованию систем, когда ЭВМ использовалась в качестве вычислителя по полученным аналитическим зависимостям. • Чисто математическое (аналитическое) моделирование можно реализовать когда исследуемые системы уравнений имеют замкнутые решения в явном виде. Как правило, это простые случаи, не требующие применения ЭВМ.

• Имитационная модель – описание объектов, в том числе в форме алгоритмов, при котором отражается (воспроизводится) как структура системы, что достигается отождествлением элементов системы с соответствующими элементами алгоритма), так и процесс функционирования системы во времени, то есть последовательность событий. • Иными словами имитационная модель обеспечивает подобие процессов, а не характеристик объекта, как аналитическая.

• В отличие от аналитических моделей содержание операций, выполняемых при имитационном моделировании, не требует преобразования исходной математической модели к такой, которая содержит искомые величины в явном виде. • Поведение элементов исследуемого объекта, а также взаимосвязи между ними описываются набором алгоритмов, реализуемых на некотором языке моделирования. • Имитационное моделирование в отличие от других методов имеет ряд преимуществ, из которых можно выделить следующие: • возможность описания модели исследуемого объекта на высоком уровне детализации; • практическое отсутствие ограничений на вид зависимостей между параметрами модели.

• Имитационные модели не способны формировать решение в том виде, в котором это имеет место в аналитических моделях, а могут лишь служить инструментальным средством для анализа поведения системы в условиях определяемых экспериментатором, позволяя следить за ходом процесса. • В этом смысле имитационное моделирование не теория, а методология решения проблемы, когда задача синтеза решается путем направленного перебора при вариации основных независимых переменных.

• Различие аналитического и имитационного подходов иллюстрирует пример вычисления коэффициента гармоник меандра • Коэффициент гармоник КГ меандра можно вычислить аналитическим методом, с допущением об идеальных фронтах переключения. • Известны формулы, по которым для меандра с амплитудой и действующим значением действующее значение первой гармоники , • а коэффициент гармоник

• При имитационном моделировании воспроизводится процесс формирования прямоугольного сигнала в схеме и коэффициент гармоник вычисляется по формуле • где n – конечное число гармоник Ui, определяемых разложением реального сигнала в ряд Фурье.

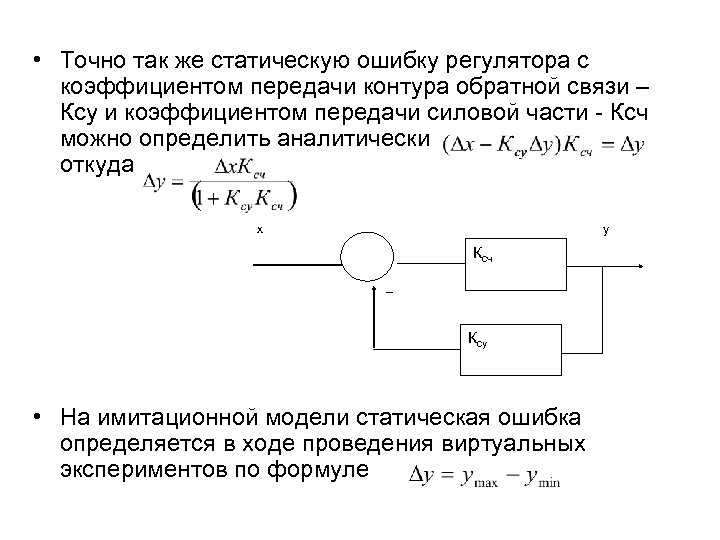• Точно так же статическую ошибку регулятора с коэффициентом передачи контура обратной связи – Ксу и коэффициентом передачи силовой части - Ксч можно определить аналитически откуда х у Ксч Ксу • На имитационной модели статическая ошибка определяется в ходе проведения виртуальных экспериментов по формуле

• В процессе математического моделирования возникает задача оценки соответствия используемых для исследования математических моделей реальному объекту. • Эта задача обычно решается следующими способами: • 1. Верификация (установление работоспособности) – проверка соответствия поведения модели логике поведения системы. • 2. Оценка адекватности – проверка соответствия между поведением модели и реальной системы путем сравнения характеристик объекта и модели.

• Правильная организация работы с моделью предусматривает: • • формирование модели и определение границ ее применяемости; • • стратегическое планирование – планирование эксперимента, который должен дать полную информацию о системе (программа испытаний); • • тактическое планирование – определение способа проведения каждой серии испытаний, предусмотренных планом эксперимента (методика испытаний); • • экспериментирование – процесс получения требуемых данных; • • интерпретация – построение выводов по полученным данным; • • документирование – регистрация хода создания модели и осуществления проекта.

• В используемых в САПР универсальных и специализированных моделирующих пакетах, как правило, заложены возможности реализации и аналитических и имитационных моделей. • При разработке ЭУ средствами моделирования выполняются: • тепловой анализ; • механический анализ конструкции; • электрический анализ (статика, динамика); • анализ худшего случая; • проектный анализ электромагнитной совместимости; • анализ надежности и др.

• 2. 2. КЛАССИФИКАЦИЯ МОДЕЛЕЙ, ИСПОЛЬЗУЕМЫХ ПРИ АВТОМАТИЗИРОВАННОМ ПРОЕКТИРОВАНИИ • В зависимости от принадлежности к тому или иному иерархическому уровню выделяют модели системного, функционально-логического, макроуровня (сосредоточенного) и микроуровня (распределенного). • Кроме того, используются понятия полных моделей и макромоделей, моделей статических и динамических, детерминированных и стохастических, аналоговых и дискретных. • Особое место занимают геометрические модели, используемые в системах конструирования.

• Полная модель объекта в отличие от макромодели описывает не только процессы на внешних выводах моделируемого объекта, но и внутренние для объекта процессы. • Статические модели описывают статические состояния, в них не присутствует время в качестве независимой переменной. Динамические модели отражают поведение системы, т. е. в них обязательно используется время. • Стохастические и детерминированные модели различаются в зависимости от учета или не учета случайных факторов. • В аналоговых моделях фазовые переменные – непрерывные величины, в дискретных – дискретные, в частном случае дискретные модели являются логическими (булевыми), в них состояние системы и ее элементов описывается булевыми величинами. • В ряде случаев применяют смешанные модели, в которых одна часть подсистем характеризуется аналоговыми моделями, другая – логическими.

• На микроуровне типичные математические модели представлены дифференциальными уравнениями в частных производных вместе с краевыми условиями. К этим моделям, называемым распределенными, относятся многие уравнения математической физики. • Объектами исследования здесь являются поля физических величин, что требуется при анализе прочности конструкций, моделировании концентраций и потоков частиц и т. п. • Число совместно исследуемых различных сред (число деталей, слоев материала, фаз агрегатного состояния) в практически используемых моделях микроуровня не может быть большим из-за сложностей вычислительного характера. • Резко снизить вычислительные затраты в многокомпонентных средах можно, применив иной подход к моделированию, основанный на принятии определенных допущений.

• Допущение, выражаемое дискретизацией пространства, позволяет перейти к моделям макроуровня. • Моделями макроуровня, называемыми также сосредоточенными, являются системы алгебраических и обыкновенных дифференциальных уравнений, поскольку независимой переменной здесь остается только время t. • Упрощение описания отдельных компонентов (деталей) позволяет исследовать модели процессов в устройствах, приборах, механических узлах, число компонентов в которых может доходить до нескольких тысяч.

• В тех случаях, когда число компонентов в исследуемой системе превышает некоторый порог, сложность модели системы на макроуровне вновь становится чрезмерной. Поэтому, принимая соответствующие допущения, переходят на функционально-логический уровень. • На этом уровне используют аппарат передаточных функций для исследования аналоговых (непрерывных) процессов или аппарат математической логики и конечных автоматов, если объектом исследования является дискретный процесс, т. е. процесс с дискретным множеством состояний. • Наконец, для исследования еще более сложных объектов, примерами которых могут служить вычислительные системы и сети, применяют аппарат теории массового обслуживания, возможно использование и некоторых других подходов, например, сетей Петри. Эти модели относятся к системному уровню моделирования.

• Процесс моделирования состоит из этапов формирования модели и ее исследования (решения). В свою очередь, формирование модели включает две процедуры: вопервых, разработку моделей отдельных компонентов, вовторых, формирование модели системы из моделей компонентов. • Первая из этих процедур выполняется предварительно по отношению к типовым компонентам вне маршрута проектирования конкретных объектов. • Как правило, модели компонентов разрабатываются специалистами в прикладных областях, причем знающими требования к моделям и формам их представления в САПР. • Обычно в помощь разработчику моделей в САПР предлагаются методики и вспомогательные средства, например, в виде программ анализа для экспериментальной отработки моделей. • Созданные модели включаются в библиотеки моделей прикладных программ анализа.

• На маршруте проектирования каждого нового объекта выполняется вторая процедура – формирование модели системы с использованием библиотечных моделей компонентов. Как правило, эта процедура выполняется автоматически по алгоритмам, включенным в заранее разработанные программы анализа. • При применении этих программ пользователь описывает исследуемый объект на входном языке программы анализа не в виде системы уравнений, которая будет получена автоматически, а в виде списка элементов структуры, эквивалентной схемы, эскиза или чертежа конструкции.

• Исходными для формирования математических моделей объектов на макроуровне являются компонентные и топологические уравнения. • Компонентными уравнениями называют уравнения, описывающие свойства элементов (компонентов), другими словами, это уравнения математических моделей элементов. • Топологические уравнения описывают взаимосвязи в составе моделируемой системы. • В совокупности компонентные и топологические уравнения конкретной физической системы представляют собой исходную математическую модель системы.

• Очевидно, что компонентные и топологические уравнения в системах различной физической природы отражают разные физические свойства, но могут иметь одинаковый формальный вид. • Одинаковая форма записи математических соотношений позволяет говорить о формальных аналогиях компонентных и топологических уравнений. • Такие аналогии существуют для механических поступательных, механических вращательных, электрических, гидравлических (пневматических), тепловых объектов и др. • Наличие аналогий приводит к практически важному выводу: значительная часть алгоритмов формирования и исследования моделей в САПР оказывается инвариантной и может быть применена к анализу проектируемых объектов в разных предметных областях. • Единство математического аппарата формирования моделей особенно удобно при анализе систем, состоящих из физически разнородных подсистем.

• • • Компонентные уравнения имеют вид FК (d. V / dt, V, t) = 0, а топологические FТ (V) = 0, где V = (v 1, v 2, . . . vn) – вектор фазовых переменных, t – время. • К фазовым переменным можно отнести токи и напряжения в электрических системах, силу и скорость – в механических, давление и расход – в гидравлических, тепловой поток (мощность) и температуру – в тепловых. • Различают фазовые переменные двух типов, фазовые переменные типа потенциала (например, электрическое напряжение) и типа потока (например, электрический ток).

• Каждое компонентное уравнение характеризует связи между разнотипными фазовыми переменными, относящимися к одному компоненту (например, закон Ома описывает связь между напряжением и током в резисторе), а топологическое уравнение – связи между однотипными фазовыми переменными в разных компонентах. • Модели можно представлять в виде систем уравнений или в виде эквивалентных схем. • Компонентные уравнения простых двухполюсников: • для R: u = i R (закон Ома), • для C: i = C du/dt, • для L: u = L di/dt, • где u – напряжение (точнее, падение напряжения на двухполюснике), i – ток. • Топологические уравнения выражают законы Кирхгофа для напряжений (ЗНК) и токов (ЗТК). Согласно ЗНК, сумма напряжений на компонентах вдоль любого замкнутого контура в эквивалентной схеме равна нулю, а в соответствии с ЗТК сумма токов в любом замкнутом сечении эквивалентной схемы равна нулю.

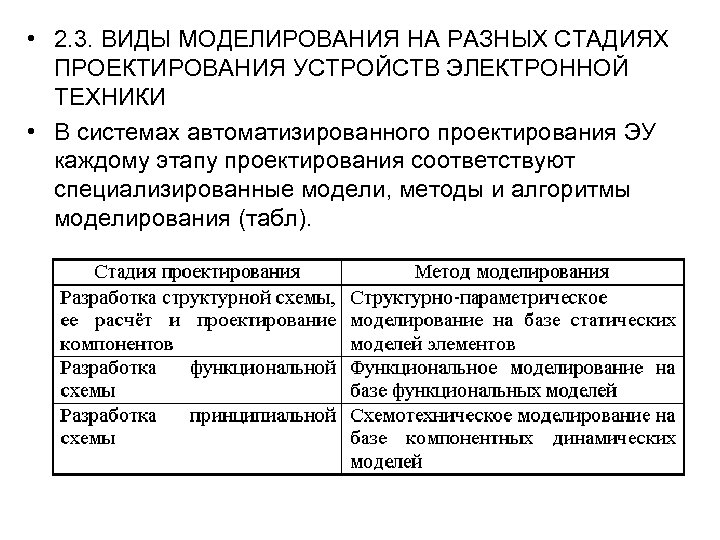• 2. 3. ВИДЫ МОДЕЛИРОВАНИЯ НА РАЗНЫХ СТАДИЯХ ПРОЕКТИРОВАНИЯ УСТРОЙСТВ ЭЛЕКТРОННОЙ ТЕХНИКИ • В системах автоматизированного проектирования ЭУ каждому этапу проектирования соответствуют специализированные модели, методы и алгоритмы моделирования (табл).

• Наиболее универсальными являются полные модели элементов, описывающие все тонкие физические взаимодействия и содержащие всю необходимую для разработчика и конструктора информацию об элементе. • Но даже когда физические принципы работы элемента хорошо известны, для идентификации его внутренней структуры необходимо использовать большое количество параметров, причём определение этих параметров часто связано с большими экспериментальными исследованиями. • Кроме того, на разных этапах проектирования требуется разная информация об элементе.

• Поэтому в подсистемах САПР различного назначения используют специализированные (локальные) модели элементов, которые разделяют на следующие группы: • Статические (интегральные) для программ проектирования. Предназначены для расчёта установившихся режимов и энергетических соотношений в схемах электронных устройств с использованием действующих и средних значений токов и напряжений и алгебраических уравнений. • Динамические (дифференциальные) для систем моделирования. Предназначены для расчёта переходных процессов с использованием мгновенных значений токов и напряжений и интегро-дифференциальных уравнений.

• Структурно-параметрическое моделирование – исследование состава элементов устройства, способов их соединения и взаимодействия, т. е. выбор схемы, ее расчёт и проектирование компонентов. • Функциональное моделирование – исследование процесса преобразования сигнала по мере его прохождения от входа к выходу схемы. На этапе функционального моделирования решаются вопросы функционирования разрабатываемых электронных устройств и определяются оптимальные стратегии их управления.

• При этом схема разбивается на отдельные блоки, и производится расчет формы сигнала и его основных параметров в узлах полученной функциональной схемы. • При функциональном моделировании, в соответствии с принципами информационного подхода, делается допущение о согласовании входных и выходных параметров блоков и потому не требуется решения уравнений равновесия. • При функциональном моделировании широко используются представления отдельных блоков схемы их передаточными функциями или управляемыми эквивалентными источниками. • Характерным примером задач, решаемых методами функционального моделирования, является исследование систем автоматического регулирования, функциональные схемы которых состоят из типовых звеньев – дифференцирующих, интегрирующих, форсирующих, чистой задержки и т. д.

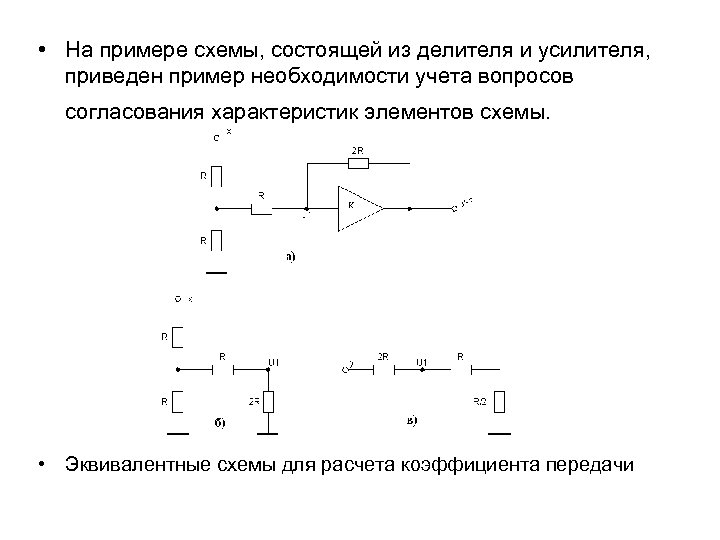• На примере схемы, состоящей из делителя и усилителя, приведен пример необходимости учета вопросов согласования характеристик элементов схемы. • Эквивалентные схемы для расчета коэффициента передачи

• Если считать делитель и усилитель согласованными, то коэффициент передачи схемы равен – 1. Но приведенный ниже расчет дает значение Кп = – 2/3. • Действительно, в соответствии с принципом суперпозиции, • в схеме б) и • в схеме в) • При К и • Значение Кп = – 1 можно получить при выполнении условия согласования делителя и усилителя: R делителя << R на входе усилителя.

• Схемотехническое моделирование – моделирование электрических процессов в электронных устройствах, изображённых в виде электрических схем (принципиальных и эквивалентных). • При схемотехническом моделировании используются компонентные динамические модели элементов и требуется решение уравнений равновесия (топологических – законы Кирхгофа) и компонентных уравнений. • Для анализа логических (цифровых) устройств используется функциональнологическое моделирование.

• Классификация функциональных (макро) моделей • Моделирование нелинейных схем требует больших временных затрат, так как для исследования процесса необходимо просчитать большое число временных интервалов. • Поэтому для снижения затрат на этапе синтеза функциональной схемы часто используются макромодели элементов и функциональных устройств. • Макромодель – это более простая, по сравнению с моделью на компонентном уровне, модель схемы (или её части), воспроизводящая её поведение на уровне входных, выходных и передаточных характеристик, и также учитывающая наиболее важные для конкретных видов расчёта характеристики и реакции схемы на внешние воздействия.

• При использовании макромоделей увеличивается скорость счёта (за счёт упрощения), но должны быть решены проблемы точности и правильного выбора области использования моделей, особенно линеаризованных. • Выделяют три способа формирования макромоделей: • 1. Упрощающие макромодели. В основу их формирования положен принцип редукции: • использование более простых (идеализированных) моделей компонентов; • замена блоков (узлов) схемы эквивалентными источниками тока или напряжения; • исключение отдельных компонентов схемы, слабо влияющих на выходные параметры схемы в данных режимах работы. • Для макромоделей, полученных на основе упрощений, основным достоинством является возможность сохранения компонентной структуры модели.

• 2. Формальные макромодели. Основаны на формальной аппроксимации внешних характеристик схем. Схемные элементы таких моделей не имеют сходства с элементами истинной схемы и более того инвариантны к различным элементным базисам. • При таком подходе удается реализовывать модели представленные: • • структурой дифференциальных уравнений (реализуются моделями математических операций, в том числе на базе решающих операционных усилителей); • • моделями "черного ящика" в виде входных выходных и передаточных характеристик – эти модели реализуются аппроксимацией характеристик встроенными функциями и формальными моделями на основе управляемых источников тока и напряжения; • • функциональными моделями узлов схемы, логическими моделями.

• 3. Смешанное логико-схемное моделирование. Моделирующая система содержит программу, совмещающую схемотехническое и функциональнологическое моделирование т. е. совмещает два различных математических базиса. Между обеими частями информация передаётся через трансляторы, преобразующие электрические значения напряжений в их логические эквиваленты и наоборот. • Таким образом, функциональное моделирование основано на использовании спектра моделей, позволяющего в зависимости от решаемой задачи использовать как приёмы макромоделирования, так и компонентное представление элементов.

• При решении задач функционального моделирования используются как специализированные, так и универсальные пакеты программ, библиотека моделей которых дополняется моделями математических операций, используемых в дифференциальных уравнениях (интегрирование, умножение, ограничение, суммирование и т. д. ). • Например, использование в качестве базисного пакета моделирования PSPICE при работе в среде PCAD, Or. CAD обеспечивает связь и передачу начерченной схемы для анализа, что соответствует структуре сквозной САПР. Пакет PSPICE реализует все необходимые виды анализа электронной аппаратуры: временной, частотный, Фурье, статистический и т. д. • Возможность реализации формальных макромоделей, оформленных в виде подсхем, позволяет эффективно использовать этот пакет для структурного и функционального моделирования сложных динамических систем.

Способы реализации различных форм представления моделей приведены в табл.

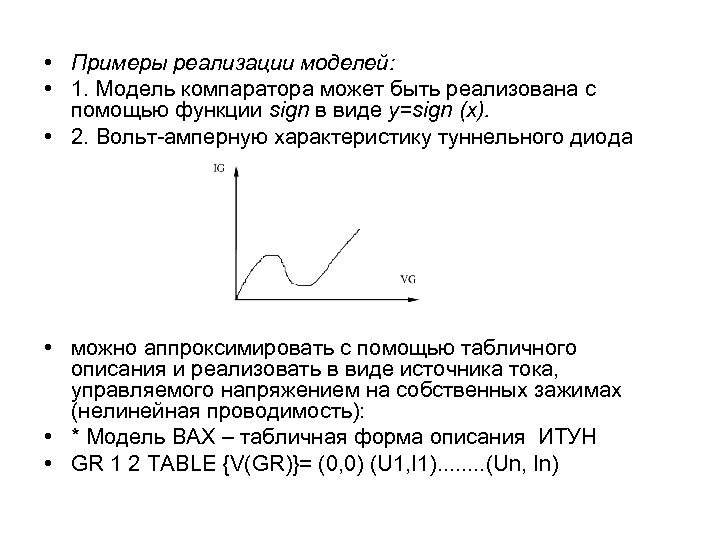• Примеры реализации моделей: • 1. Модель компаратора может быть реализована с помощью функции sign в виде y=sign (x). • 2. Вольт-амперную характеристику туннельного диода • можно аппроксимировать с помощью табличного описания и реализовать в виде источника тока, управляемого напряжением на собственных зажимах (нелинейная проводимость): • * Модель ВАХ – табличная форма описания ИТУН • GR 1 2 TABLE {V(GR)}= (0, 0) (U 1, I 1). . . . (Un, In)

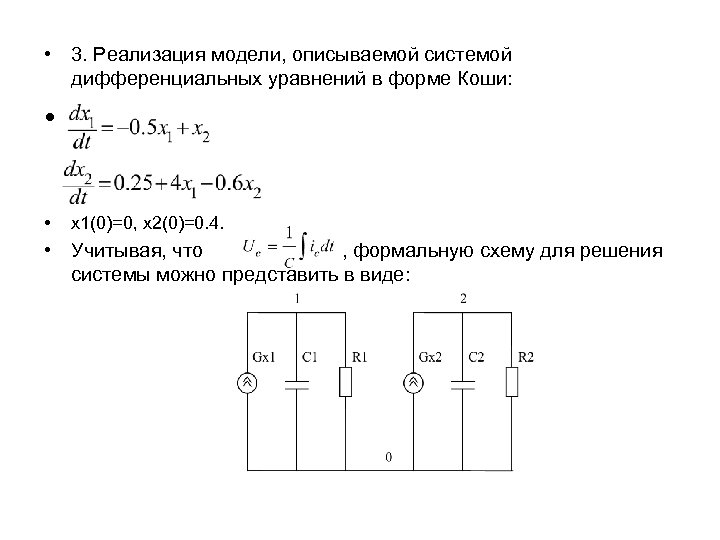• 3. Реализация модели, описываемой системой дифференциальных уравнений в форме Коши: • • x 1(0)=0, x 2(0)=0. 4. • Учитывая, что , формальную схему для решения системы можно представить в виде:

• На рисунке значения переменных х1 и х2 равны напряжениям в узлах 1 и 2 соответственно. • Описание модели в системе PSPICE будет иметь вид: • GX 1 0 1 POLY(2) (1, 0) (2, 0) 0 – 0. 5 1 • GX 2 0 2 POLY(2) (1, 0) (2, 0) 0. 25 4 – 0. 6 • C 1 1 0 1 • C 2 2 0 1 • R 1 1 0 1 E 9 • R 2 2 0 1 E 9 • . IC V(1)=0 V(2)=0. 4 • *В схеме GX 1, GX 2 – источники тока, управляемые напряжениями в узлах 1 и 2.

• 4. Реализация модели инерционно – форсирующего звена с передаточной функцией • По аналогии с методами аналогового моделирования на базе решающих операционных усилителей, модель можно реализовать на основе формальной схемы с идеальным усилителем. В схеме T 1=R 1 C 1, T 2=R 2 C 2, K=R 2/ R 1.

• Описание модели в системе PSPICE будет иметь вид (Е - ИНУН): • E 3 0 2 0 – 100 K • R 1 1 2 (R 1) • R 2 2 3 (R 2) • R 3 2 0 (R 3) • C 1 1 2 (C 1) • C 2 2 3 (C 2)

• 5. Модель генератора пилообразного напряжения может быть реализована с помощью эквивалентного источника напряжения. • Описание модели генератора «пилы» с амплитудой 1 В, длительностью 100 мкс, вершиной и спадом 1 мкс в системе PSPICE будет иметь вид: • Up 1 0 PULSE (0 1 0 98 U 1 U 1 U 100 U)

• 6. Электро-тепловая аналогия. • Основные соотношения электро-тепловой аналогии: • • • где Pp – источник тока, имитирующий рассеиваемую в элементе схемы мощность; Rт – тепловое сопротивление; Т 1 – перегрев элемента; Токр – источник напряжения, устанавливающий температуру окружающей среды; λ – коэффициент теплопроводности материала, Вт/мо. С; δ, S – длина, м и поперечное сечение материала, м 2, через который проходит тепловой поток.

• 7. Расчет магнитной цепи. В соответствии с законом полного тока • • где аналогии: - магнитное • сопротивление (сравни - электрическое сопротивление). • - магнитодвижущая сила (МДС) намагничивающей обмотки, • - магнитное напряжение, • - участок магнитной цепи. • (Помним, что )

• 2. 4. СХЕМОТЕХНИЧЕСКОЕ МОДЕЛИРОВАНИЕ • Схемотехническое моделирование (Сх. М) – это моделирование электрических процессов в электронных устройствах, изображённых в виде принципиальных электрических схем. • При (Сх. М) используются компонентные динамические модели элементов и в отличие от информационного моделирования требуется решение уравнений равновесия (или топологических уравнений), которыми являются первый и второй законы Кирхгофа и компонентных (уравнения отдельных элементов схемы) уравнений. • Более высокая строгость описания электронных схем позволяет получить более точное представление о процессах в схеме, однако время моделирования увеличивается.

• • • Цель Сх. М в точном определении формы и параметров сигналов во всех точках схемы, для чего решаются типовые задачи Сх. М: расчет режима цепи по постоянному току в том числе при вариации одного или нескольких источников постоянного напряжения или тока, температуры, параметров элементов схемы; анализ чувствительности характеристик цепи к вариации параметров элементов; анализ характеристик линеаризованной цепи в частотной области при воздействии одного или нескольких сигналов; анализ переходных процессов (временной анализ) при воздействии сигналов различной формы и при разных начальных условиях; спектральный анализ кривых токов и напряжений в схеме с помощью преобразования Фурье; многовариантный анализ при вариации любого параметра для любого из перечисленных видов анализа, например многовариантный анализ переходных процессов при изменении параметров корректирующего звена; статистический анализ, при котором случайное значение каждого параметра рассчитывается по формуле: где – центрированная случайная величина, принимающая значения на отрезке (– 1, +1), –относительный разброс параметра x; анализ «худшего» случая, при котором значение каждого параметра рассчитывается по формуле.

• На основе решения этих задач становятся возможными: • проверка соответствия электрических режимов элементов расчетным, принятым для проектирования компонентов схемы; • проверка, в том числе в аварийных режимах, соответствия электрических режимов элементов предельно допустимым по техническим условиям на них; • проверка статической точности, спектра и качества динамических характеристик выходных сигналов; • контроль чувствительности схемы к изменению параметров ее элементов, статистический анализ (определение для схемы вероятности работоспособности в соответствии с ТЗ при статистическом разбросе ее параметров), анализ наихудшего случая, когда учитываются максимальные «уходы» параметров элементов при воздействии всех дестабилизирующих эксплуатационных факторов.

• Современные программы Сх. М, такие как, например PSPICE, позволяют создавать входной файл с помощью текстового редактора и графического описания топологии (рисования схемы) с помощью графических редакторов. • Предложения входного языка делятся на описание компонентов и директивы управления заданием. • Имена элементов начинаются с общепринятых буквенных обозначений (R, L, C, D и т. д. ). • Программа включает встроенные модели основных типов и библиотеку параметров электрорадио элементов – LIB. • С помощью директив управления задается вид анализа, способ задания начальных условий, способ вывода результатов.

• При использовании даже самых совершенных программ схемотехнического моделирования надо помнить о проблеме сходимости решения. Эта проблема обостряется, если: • заданы слишком крутые фронты независимых источников, или не фиксируются, как в реальных схемах, фронты переключения импульсных генераторов и компараторов, например RCцепочками; • в схеме имеются реактивные элементы с очень большим разбросом постоянных времени (проблема «жестких» матриц); • в схеме не «развязаны» резисторами индуктивные звезды и емкостные контуры; • не учтено затухание колебательных контуров с помощью эквивалентных резисторов.

• Для парирования проблемы конвергенции (сходимости решения) рекомендуется использовать заложенные в программах моделирования возможности управления расчетом: • увеличить количество итераций на одном шаге расчета, • ухудшить статическую точность расчета, • уменьшить максимальный шаг расчета, • отключить расчет базовой точки (по постоянному току), при этом нужно задать начальные условия. • Естественно, нужно устранить перечисленные недостатки моделей.

• Очевидно, что при Сх. М необходимы проверенные, точные модели элементов, гарантирующие достоверность результатов. • Такие модели разработаны и встраиваются, как правило, в современные пакеты прикладных программ схемотехнического моделирования. • Все расчеты параметров моделей элементов производят по данным и характеристикам, взятым из технических условий на элемент, либо по результатам экспериментальных исследований. • При этом используются специальные программы, имеющиеся в современных пакетах, таких как PSPICE (Model Editor).

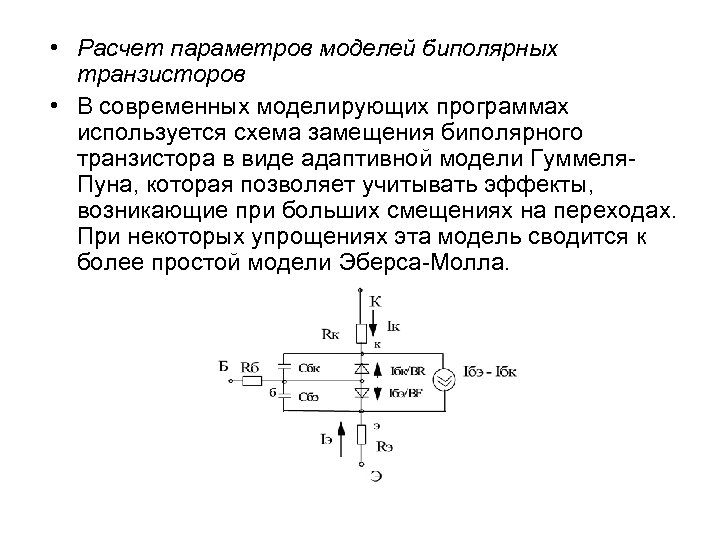• Расчет параметров моделей биполярных транзисторов • В современных моделирующих программах используется схема замещения биполярного транзистора в виде адаптивной модели Гуммеля. Пуна, которая позволяет учитывать эффекты, возникающие при больших смещениях на переходах. При некоторых упрощениях эта модель сводится к более простой модели Эберса-Молла.

• Статический режим в этой схеме описывается следующими соотношениями: • • • где IS – ток насыщения при Т=270 С, Vt – тепловой потенциал. ; ; ; ,

• В соответствии с эквивалентной схемой и приведенными уравнениями основными параметрами модели биполярного транзистора, зависящими от его типа, являются: • Статические параметры: • BF – пpямой коэффициент усиления по току; • BR – инвеpсный коэффициент усиления по току; • RC – омическое сопpотивление коллектоpа, Oм; • RB – несмещенное сопpотивление базы, Oм; • RE – сопртивление эмиттера, Ом. • Динамические параметры: • CJC – емкость коллектоpного пеpехода, Ф; • CJE – емкость эмиттеpного пеpехода, Ф; • TF – постоянная вpемени диффузионной емкости эмиттеpного пеpехода, с; • TR – постоянная вpемени диффузионной емкости коллектоного пеpехода, с.

• Для расчета сопротивления базы выбирают точки тока Iб и напряжения Uбэ по входной характеристике транзистора в схеме с ОЭ при Uкэ=0. . . 10 В. • Если входная характеристика Iб=f(Uбэ) представлена в ТУ серией кривых, зависящих от напряжения Uкэ, то выбор точек производят при Uкэ=0 В. Точки тока Iб и напряжения Uбэ выбирают на линейном участке входной характеристики транзистора с высоким уровнем инжекции. • RB= Uбэ/ Iб. • Для расчета сопротивления коллектора выбирают две точки тока коллектора Iк и две точки напряжения Uкэ. нас на линейном участке характеристики "Зависимость напряжения насыщения от тока коллектора при Iк/Iб=const" на участке токов с B=const. • RС= Uкэ/ Iк. • Сопротивление эмиттера можно принять равным нулю.

• Для расчета B в инверсном режиме можно пользоваться соотношением • BR=BF(Iтэ/Iтк), где Iтэ, Iтк – тепловые токи эмиттерного и коллекторного переходов. • Коэффициент усиления в прямом включении – BF выбирают по ТУ и, как правило типовое значение BR = (Bmin + Bmax)/2. • Динамические параметры биполярного транзистора, учитывая, что емкости Сбк и Сбэ включают зарядную и диффузионную составляющие, определяются по следующей методике: • Зарядные емкости транзистора CJC и CJE выбирают из ТУ, равными постоянной усредненной величине.

• Для расчета постоянной времени диффузионной емкости эмиттерного перехода определяют по ТУ модуль коэффициента передачи тока | h 21 э | в схеме с ОЭ, граничную частоту fгр, коэффициент передачи тока на низкой частоте определяют по характеристике из ТУ "Зависимость Bст от тока коллектора" в точке тока, указанного для pежима измеpения | h 21 э |). • Для расчета постоянной времени диффузионной емкости коллекторного перехода определяются по ТУ время рассасывания ts, коэффициент пеpедачи тока в схеме с ОЭ при токе коллектора Ic и токи базы вкл. и откл. – Iб 1 и Iб 2. • Если в ТУ указаны время выключения транзистора и время спада коллекторного тока, то ts оределяют из соотношения: ts = tвык – tспада. • .

• Определение параметров модели диода • Основными параметрами диодов, зависящими от их типа, являются: • RS – омическое сопpотивление диода, ОМ; • TT – постоянная вpемени восстановления обpатного сопpотивления диода, c; • CJO – заpядная емкость диода, Ф; • BV – напpяжение обpатного пpобоя, B. • Для pасчета сопpотивления тела базы RS выбиpают точки тока Iпp и напpяжения Uпp на линейном участке вольт-ампеpной хаpактеpистики пpи больших уpовнях инжекции. • RS= Uпр/ Iпр.

• Заpядную емкость СJO, pавную усpедненной величине, выбирают из ТУ. • Постоянную времени восстановления обpатного сопpотивления в pежиме пеpеключения определяют по формуле • • при времени восстановления ts, суммаpном сопpотивлении pазpяда – Rs, пpямом токе – IFM, обратном токе отсчета – IR 0 и обpатном напpяжении – URM. • Если в ТУ отсутствуют параметры Rs, IFM, URM, IR 0, то их значения выбирают из ГОСТа, указанного в ТУ в разделе "Измерения электрических параметров" для определения времени восстановления обратного сопротивления диода в режиме переключения.

• Расчет параметров модели полевого транзистора • Для модели полевого транзистора с p-n переходом определяются следующие параметры: • VTO – напряжение отсечки, В; • BETA – удельная крутизна, A/B²; • LAMBDA – коэффициент модуляции, 1/B; • RD – омическое сопротивление стока, ОМ; • RS – омическое сопротивление истока, ОМ; • CGD – проходная емкость сток-затвор, Ф; • CGS – входная емкость исток-затвор, Ф. • Для расчета удельной крутизны BETA из ТУ выбирают ток стока начальный – ICN, напряжение затвор-исток отсечки – UZIO. • BETA=ICN / UZIO 2. • Проходную и входную емкости выбирают из ТУ постоянными усредненными величинами.

• Дроссель представляется обычно моделью, содержащей последовательно соединенную индуктивность L и сопротивление r 0. • Сопротивление r 0 определяет активные потери в обмотке дросселя. • Потери в сердечнике учитываются эквивалентным сопротивлением Rs. • Индуктивность дросселя может быть задана постоянным значением. Нелинейность индуктивности является функцией тока и описывается полиномом n порядка. • При заданных коэффициентах полинома индуктивность вычисляется по формуле

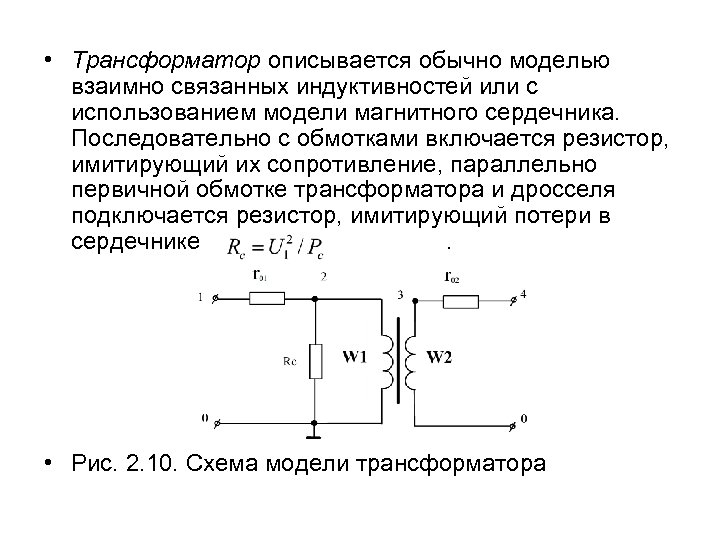• Трансформатор описывается обычно моделью взаимно связанных индуктивностей или с использованием модели магнитного сердечника. Последовательно с обмотками включается резистор, имитирующий их сопротивление, параллельно первичной обмотке трансформатора и дросселя подключается резистор, имитирующий потери в сердечнике. • Рис. 2. 10. Схема модели трансформатора

• Модель трансформатора, схема которого представлена на рис. 2. 10, при использовании модели сердечника из феррита М 2000 -НМ имеет вид. • * Описание модели трансформатора • Ro 1 1 2 0. 1 • Ro 2 3 4 0. 1 • Rc 2 0 5 K • L 1 2 0 50 • L 2 3 0 100 • K 1 L 2 0. 9999 M 2000 • model M 2000 CORE (MS=334 e 3 ALFA=2. 3 e-2 A=4050 K=166 C=0. 05 • + AREA=0. 064 PATH=2. 25).

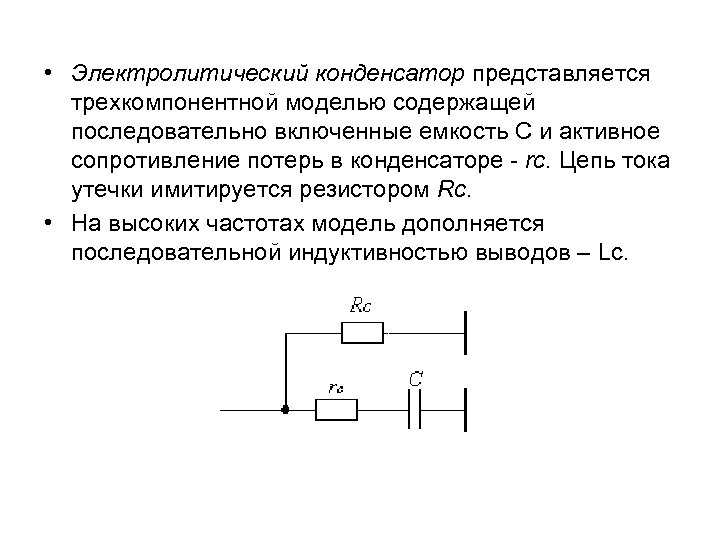• Электролитический конденсатор представляется трехкомпонентной моделью содержащей последовательно включенные емкость C и активное сопротивление потерь в конденсаторе - rc. Цепь тока утечки имитируется резистором Rc. • На высоких частотах модель дополняется последовательной индуктивностью выводов – Lc.

• Модели микросхем оформляют как подсхему, описываемую на входном языке моделирующей программы по принципиальной схеме или схеме замещения, или алгоритму работы микросхемы • *Модель операционного усилителя • subckt K 140 UD 6 A 1 2 3 4 5 • * 1– неинвертирующий вход, • * 2– инвертирующий вход, • * 3– питание плюс, • * 4– питание минус, • * 5– выход • [ текст описания модели] • ends. • Вызов макромодели в схеме: • X 1 4 0 15 16 8 K 140 UD 6 A, • где 4, 0, 15, 16, 8 – номера узлов подключения соответствующих выводов усилителя в схеме.

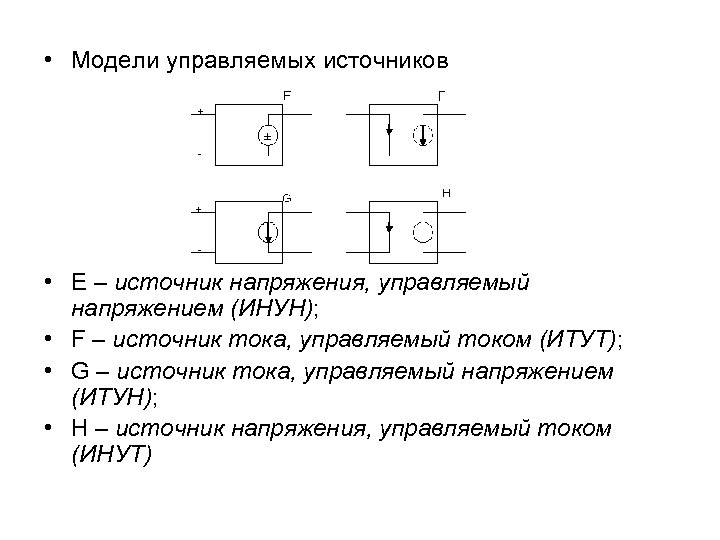• Модели управляемых источников • Е – источник напряжения, управляемый напряжением (ИНУН); • F – источник тока, управляемый током (ИТУТ); • G – источник тока, управляемый напряжением (ИТУН); • Н – источник напряжения, управляемый током (ИНУТ)

• Входные и выходные параметры зависимых источников связываются полиномами вида: • Моделирующие программные пакеты: Workbench, Pspice, Circuit Maker, Micro. Cap, Matlab– Simulink, System. Viev, Workview office, Labview. • Proteus – моделирование микро – контроллеров 8051, AVR, PIC и др. • Table Curve – программа для регрессионного анализа (определения коэффициентов полиномов). • В САПР база данных по ЭРИ должна включать: имитационную модель, схематический символ, электрические параметры, макет для разводки, 3 D – модель.

• 2. 5. ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИСКРЕТНЫХ УСТРОЙСТВ • Для моделирования устройств вычислительной техники и дискретных устройств автоматики используется аппарат алгебры логики в виде теории комбинационных устройств для проектирования логических схем, не запоминающих информацию и теории конечных автоматов для схем с памятью. • Исходная информация для разработки логических схем – функциональная схема, алгоритм её работы, система базовых логических элементов. • Для разработки логических схем используются: • • типовые функциональные решения и прямой (интуитивный) способ синтеза; • • автоматизированный синтез.

• Процесс автоматизированного синтеза состоит из следующих этапов: • Формируются логические условия работы устройства в виде таблицы истинности или логической функции. • Производится минимизация логической функции методом непосредственных преобразований (дизъюнкция-или, конъюнкция-и, инвертирование-не), карт Карно, применением законов и правил алгебры логики. • По упрощенной логической формуле строится принципиальная схема устройства, причем минимальному числу и однородности логических элементов отдается предпочтение.

• Корректность разработанных схем оценивается моделированием. • Причём с помощью моделирования оценивается не только правильность функционирования схемы, но и исследуются переходные процессы при различных начальных условиях, надёжность работы схемы и оценка электрических режимов, граничные режимы и вероятность сбоя, генерируются тесты для проверки устройства. • Задачи и методы логического моделирования: • Проверка логики работы схемы. • Анализ переходных процессов. • Граничные испытания, проверка допустимых нагрузок по выходам элементов схемы. • 4. Генерация тестов.

• В зависимости от характера решаемых задач выбирается метод моделирования. Основными отличительными чертами методов функционально-логического моделирования являются: • а) способ учёта времени распространения сигналов; • б) способ кодирования сигналов; • в) способ построения модели; • г) очерёдность моделирования элементов.

• Модели сигналов • В зависимости от способа представления сигналов различают двоичное и многозначное моделирование – в алгебре логики как внешние сигналы, так и сигналы на входах и выходах элементов представляются: • 1. В виде логических нулей и единиц "1", "0" (двоичное кодирование). • 2. В виде трех значений (троичное кодирование) "1", "0" и "X" – обозначает переход из одного состояния в другое, либо неопределенное состояние. • 3. В системах более детального моделирования используется многозначное кодирование "0", "1", "X" и "H" -переход 0 -1, "L"-переход 1 -0, и "Z"-высокий импеданс.

• Модели элементов могут задаваться одним из следующих способов: • Внутренней структурой компонента на уровне элементов низшего ранга – простейших функционально законченных элементов логической схемы (устройства "И", "ИЛИ", "НЕ"). В качестве отдельных элементов могут использоваться триггеры, дешифраторы и т. д. • Функциональными моделями "чёрного ящика", для которых связь между входными и выходными сигналами задаётся в виде Булевых уравнений (автоматная модель) или таблиц истинности. Например, для схемы ИЛИ: • Уравнение. F=A+B. Таблица истинности • Схема

• В зависимости от способа учёта распространения сигнала различают: • • синхронное моделирование без учета временных задержек сигнала; • • асинхронное моделирование с учетом временных задержек, значения которых задаются в моделях элементов. • Синхронное логическое моделирование. Модели представляются их логическими функциями без учёта задержек, а сигналы кодируются в двоичной логике. • Применяется для оценки правильности функционирования схемы. Моделирование работы схемы сводится к вычислению значений сигналов на выходах логических элементов схемы по заданным входным сигналам.

• Вследствие того, что не учитываются времена задержки, особенностью синхронного моделирования является решение логических уравнений в определенном порядке, соответствующем последовательности прохождения сигнала через элементы схемы. • Для определения этого порядка схему предварительно ранжируют, чтобы к моменту решения каждого уравнения значения всех входных сигналов были известны. • Таким образом, под ранжированием понимается определение очередности элементов, у которых рассчитываются выходные сигналы. • Входным сигналам схемы присваивается ранг r=0. Ранжирование осуществляется автоматически. • Результатом моделирования являются временные диаграммы. На диаграмме для каждого такта моделирования приводятся значения входных воздействий и выходных сигналов элементов схемы. • Схема считается работоспособной, если в установившемся режиме каждому набору входных воздействий однозначно соответствует определенное значение сигнала на выходе.

Ранжирование схемы

• Асинхронное моделирование позволяет учитывать время распространения сигналов в элементах и соединительных цепях схемы. • Каждый элемент характеризуется некоторой средней задержкой, значение которой может меняться в различных режимах. • Временное рассогласование сигналов вследствие задержек может привести к появлению ложного сигнала на выходе логического элемента. • Вероятность проявления ложных сигналов называется "риском сбоя". Различают статические и динамические риски сбоя. • В логических схемах с памятью, то есть в схемах с обратными связями, под воздействием входных сигналов могут изменить состояние сразу несколько элементов памяти. • Окончательное состояние схемы зависит от очередности переключения элементов памяти. Считается, что в схеме существуют состязания сигналов обратной связи. • Если под воздействием входного сигнала схема из одного состояния может перейти в различные состояния в зависимости от задержек в элементах, то в этом случае состязания называют критическими.

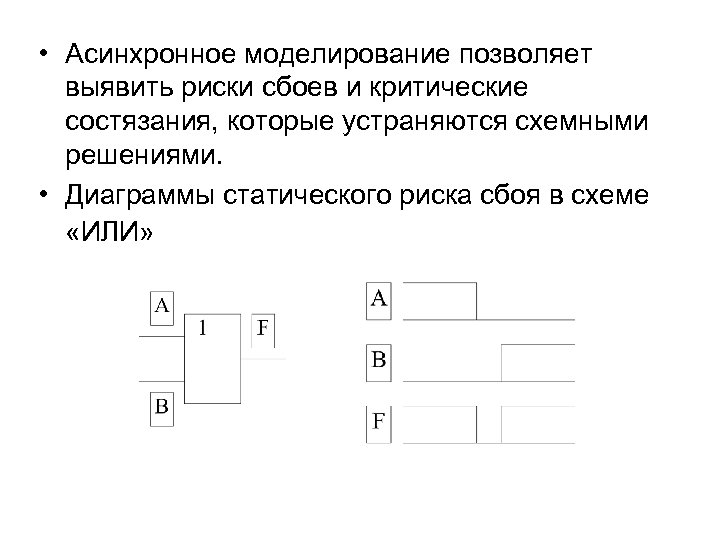• Асинхронное моделирование позволяет выявить риски сбоев и критические состязания, которые устраняются схемными решениями. • Диаграммы статического риска сбоя в схеме «ИЛИ»

• Модель логического элемента для асинхронного моделирования представляется в виде последовательного соединения безынерционного логического элемента и элемента задержки. • Асинхронное моделирование заключается в вычислении сигналов на выходах логических элементов, с определением моментов времени, когда произошли переключения. При асинхронном моделировании ранжирование схемы не производится. • По организации очередности моделирования элементов выделяют сквозной и событийный методы. • Состояния всех элементов при сквозном моделировании многократно просчитываются через интервал t (шаг). Шаг определяется как наибольший общий делитель времён задержек элементов.

• Асинхронное событийное моделирование. Обычно в активном состоянии находится только часть элементов схемы, поэтому считать с постоянным шагом всю схему не целесообразно. • Следует моделировать каждый раз только те элементы, у которых изменились входные сигналы. • На этом принципе основано событийное моделирование, при котором событие это изменение состояния какоголибо элемента и связанных с ним цепей. • Время моделирования при таком подходе существенно уменьшается, т. к. шаг определяется моментами возникновения событий. • Схема анализируется в окрестностях переключений (фронтов). При этом формируются массив состояния цепей и очередь будущих событий – моментов появления входных воздействий. • Результат моделирования – временная диаграмма с обозначением "рисков сбоя" и "критических состязаний".

• Синтез тестов. В процессе производства и эксплуатации электронной аппаратуры возникает задача проверки правильности её функционирования, обнаружения и локализации неисправностей. • Проверка производится путём подачи некоторой последовательности наборов (векторов) входных сигналов и анализа реакции устройства на эти сигналы. • Входной набор и соответствующий ему выходной сигнал называют элементарной проверкой. • Совокупность элементарных проверок – тест. Тесты бывают контролирующие и диагностические. • Контролирующие тесты – определяют наличие или отсутствие неисправностей. • Диагностические – локализуют тип и место неисправности устройства. • С целью упрощения тестов рассматривается ограниченный класс неисправностей – обрыв или короткое замыкание, то есть постоянный 0 или 1 на каком-либо выходе. • Затем по результатам моделирования составляется диагностическая таблица с набором тестов и нормальных реакций схем.

• Уровни моделей и виды схем: • Схема соединений. Ее узлы – отдельные электронные устройства в системе. • Структурная (блочная) схема. Ее узлы: выпрямители, преобразователи, фильтры, регуляторы, стабилизаторы и т. д. • Функциональная схема. Ее узлы (операции): модуляция, фильтрация, усиление, детектирование, экранирование и др. • Принципиальная электрическая схема. Элементы схемы: транзисторы, диоды, конденсаторы, резисторы, дроссели, трансформаторы и др. • 5. Эквивалентная схема. Ее элементы: сопротивление полное, эквивалентное, генераторы тока и др.