Modeling and Analyzing Distributed Systems Using I O Automata

Modeling and Analyzing Distributed Systems Using I/O Automata Nancy Lynch, MIT Draper Laboratory, IR&D Mid-Year Meeting December 11, 2002 1

Project Description • Develop I/O-automata-based methods and tools for modeling and analyzing distributed systems, with emphasis on systems for military and space applications. • Methods and tools can be used for: – System documentation/specification – Design validation: • Simulation • Stating correctness and performance theorems • Proving theorems, manually or with interactive theorem-provers – Automatic code generation • Use the methods and tools to describe and analyze Draper’s ACME system. • Project participants: – MIT: Nancy Lynch, Stephen Garland, Vida Ha, Amittai Axelrod – Draper: Joe Kochocki, Alan Tanzman 2

I/O Automata • Infinite-state, nondeterministic, interacting state machines. • Support modular system description, using parallel composition and levels of abstraction. • Static description: – Actions a (input, output, internal) – States s, start states – Transitions (s, a, s') • Dynamic description: – Execution: s 0 a 1 s 1 a 2 s 2 … – Trace: Project on external actions. – A implements B: traces(A) traces(B). • Operations for building automata: – Parallel composition, action hiding. • Reasoning methods: – Invariant assertions: Property holds in all reachable states. – Simulation relations: Imply one automaton implements another. 3

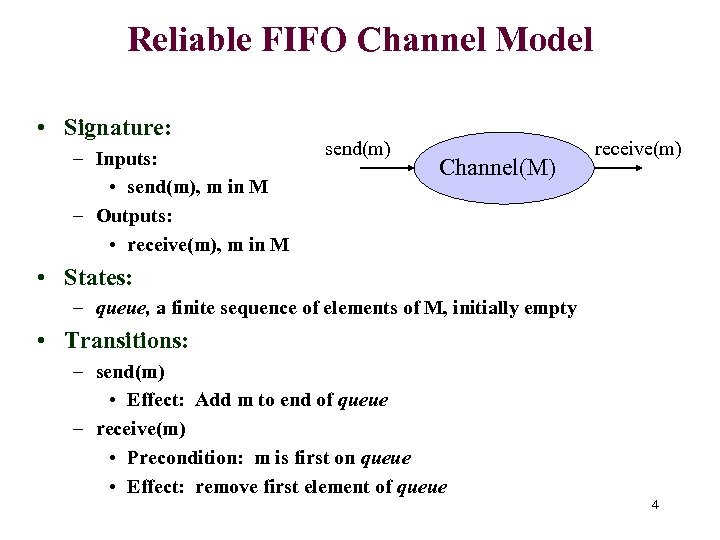
Reliable FIFO Channel Model • Signature: – Inputs: • send(m), m in M – Outputs: • receive(m), m in M send(m) Channel(M) receive(m) • States: – queue, a finite sequence of elements of M, initially empty • Transitions: – send(m) • Effect: Add m to end of queue – receive(m) • Precondition: m is first on queue • Effect: remove first element of queue 4

Example Applications • Basic distributed algorithms: – Resource allocation, consensus, atomic objects, concurrency control, group communication, … • Distributed systems: – Orca distributed shared memory system [Fekete, Kaashoek, Lynch] – Transis group communication system [Fekete, Lynch, Shvartsman] – Ensemble GCS [Hickey, Lynch, van Renesse] • Algorithms for dynamic networks: – Reconfigurable atomic memory [Lynch, Shvartsman 02] [Gilbert, Lynch, Shvartsman 02] [Musial, Shvartsman 02] – Dynamic atomic broadcast [Bar-Joseph, Keidar, Lynch 02] 5

IOA Language + Toolset • Formally-defined programming/modeling language for describing and analyzing systems modelled as I/O automata. • Current tools: Simulator, connection to Larch theorem-prover. • In progress: Invariant detector, connection to Isabelle/HOL theorem-prover, automatic code generator. I • Steve Garland will say more. O A 6

Additions to I/O Automaton Models • Timing behavior: TIOA – For describing timeout-based algorithms. – Local clocks, clock synchronization. – Timing/performance analysis. • Hybrid (continuous/discrete) behavior: HIOA – Systems with real world + computer components – Vehicle control: ground, air, space – Embedded systems 7

Timed I/O Automata (TIOA) • Add special time-passage actions, pass(t), to IOA model. • Example: Reliable FIFO channel that always delivers messages within time d. – send(m) • Effect: Add (m, now + d) to end of queue – receive(m) • Precondition: (m, u) is first on queue (for some u) • Effect: remove first element of queue – pass(t) • Precondition: for all (m, u) in queue, now + t u • Effect: now : = now + t • Can use standard automaton-based reasoning methods: – Invariant: for all (m, u) in queue, now u now + d. – Inductive proofs. 8

Example Applications • Distributed algorithms: – Resource allocation, consensus, … • Timeout-based communication protocols: – TCP, reliable multicast, … • Performance (latency) analysis: – Group communication systems: • Using GCS to build TO-Bcast [Fekete, Lynch, Shvartsman] • Scalable GCS [Khazan, Keidar 01] – RAMBO reconfiguration atomic memory • Hybrid (continuous/discrete) systems (toy examples): – RR crossing [Heitmeyer, Lynch, Archer] – Steam boiler controller 9

Hybrid I/O Automata (HIOA) • TIOA plus facilities for representing continuous behavior. • Static description: – – States: input, output, internal variables; start states Actions: input, output, internal Discrete steps (s, a, s') Trajectories , mapping time intervals to states • Dynamic description: – Execution 0 a 1 1 a 2 2 … – Trace: Project on external variables, external actions. – A implements B if traces(A) traces(B). • Operations: Composition, hiding • Reasoning methods: Invariants, simulation relations, compositional methods 10

Example Applications • Ground transportation: – People-mover (Raytheon) [Livadas, Lynch, Weinberg, Delisle]. – California PATH automated highway system: Analysis of platoon maneuvers [Dolginova, Lynch, Lygeros]. • Aircraft control: – TCAS (Lincoln Labs): Models, proofs [Livadas, Lygeros, Lynch]. – Quanser helicopter system (MIT Aero/Astro). Models, proofs [Mitra, Wang, Feron, Lynch 02]. • Spacecraft: – ACME [Ha, Axelrod, Lynch, Garland, Kochocki, Tanzman 03] 11

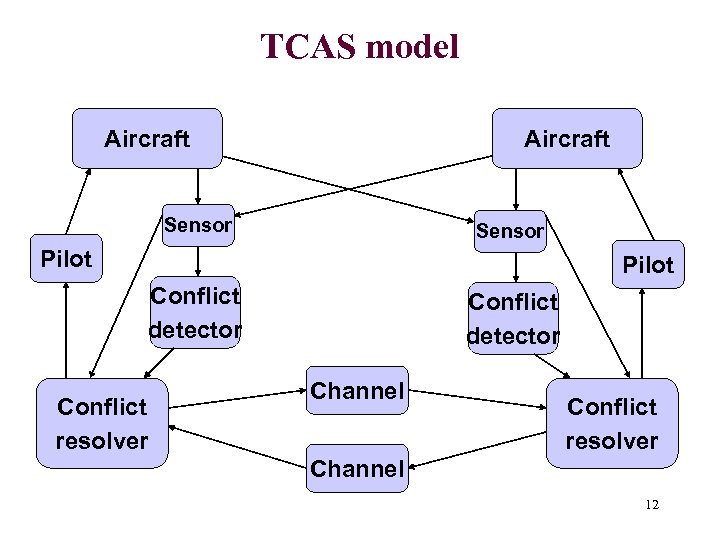
TCAS model Aircraft Sensor Pilot Conflict detector Conflict resolver Conflict detector Channel Conflict resolver Channel 12

Quanser Model Helicopter System [Mitra, Wang, Feron, Lynch 02] • 3 Do. F models manufatured by Quanser • User Controllers not safe • Supervisory pitch controller – Sensor inaccuracies – Actuator delay – Limited sampling frequency 13

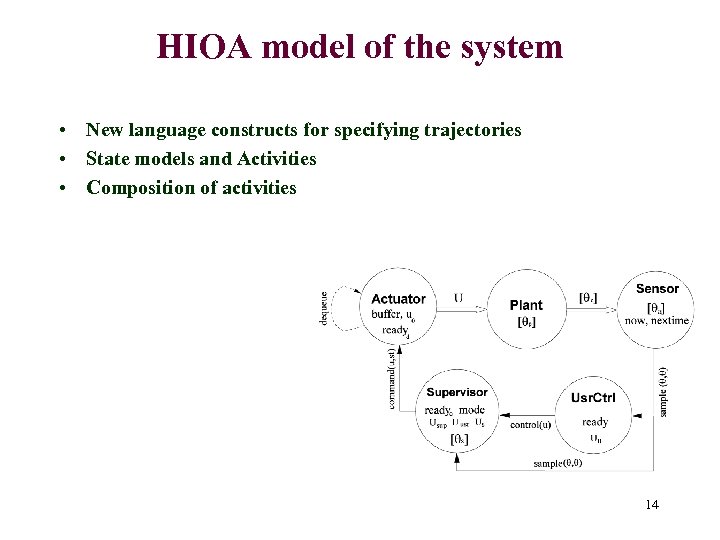
HIOA model of the system • New language constructs for specifying trajectories • State models and Activities • Composition of activities 14

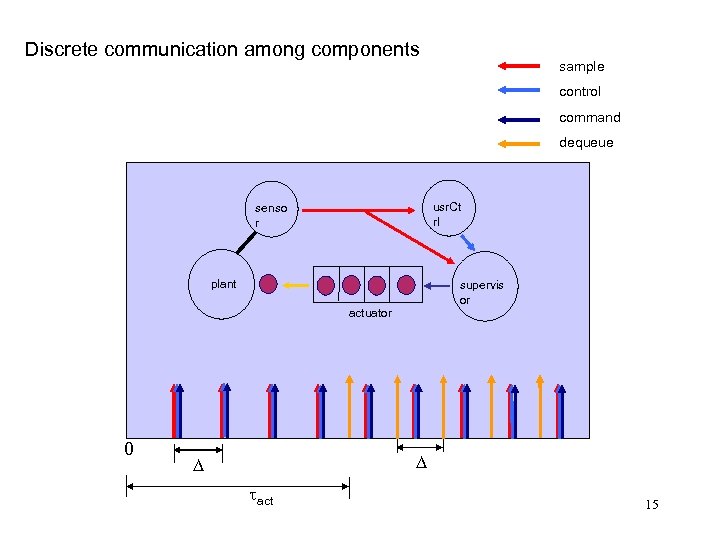
Discrete communication among components sample control command dequeue usr. Ct rl senso r plant supervis or actuator 0 D D tact 15

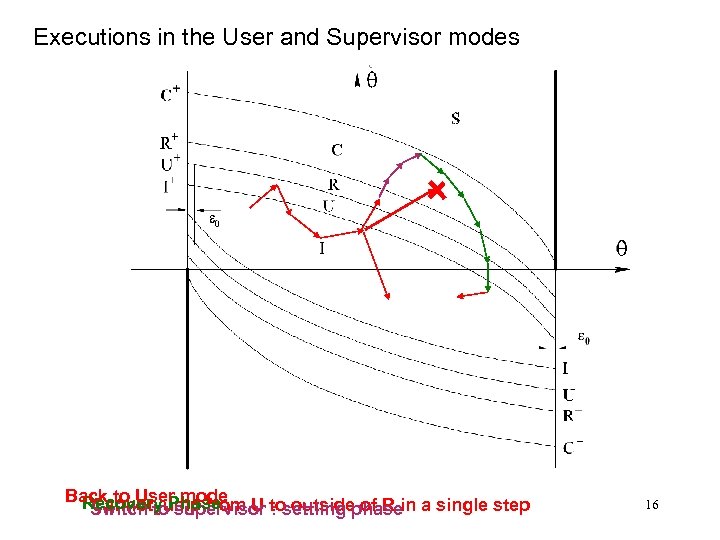
Executions in the User and Supervisor modes Back to User mode U to outside of R in a single step Recovery Phase Cannot jump from Switch to supervisor : settling phase 16

Contributions • Application of HIOA model to verification – Realistic dynamics, inaccuracies, delays • Design of safe Supervisory Controller – For arbitrary user controller • Language constructs for HIOA Future Directions • Study systems with more complicated discrete behavior and dynamics. • Develop a set of ‘useful lemmas’ from control theory to be directly used in invariant proofs • Partially automate proofs using theorem provers 17