модели сигнала Литература Ю А Евсиков Г В

модели сигнала Литература Ю. А. Евсиков, Г. В. Обрезков, В. Д. Разевиг, В. В. Чапурский, В. М. Чиликин. – Прикладные математические методы анализа в радиотехнике. – М. , Высшая школа, 1985, 343 с. 1. С. И. Баскаков. Радиотехнические цепи и сигналы. – М. , Высшая школа, 1983, 535 с. (И БОЛЕЕ ПОЗДНИЕ ИЗДАНИЯ) 2. Голубева Н. В. Математическое моделирование систем и процессов. – СПб, «Лань» , 2013, 192 стр. 3. Тепляков И. М. Основы построения телекоммуникационных систем и сетей. – Радио и связь, 2004, 328 с. 4. А. Б. Сергиенко. Цифровая обработка сигналов. – СПб. : Питер, 2002, 608 с. 5. Э. Оппенгейм, Р. Шафер. Цифровая обработка сигналов. – Связь, 1979. 416 с. 6. Л. М. Гольденберг, Б. Д. Матюшкин, М. Н. Поляк. М. Цифровая обработка сигналов. – Радио и связь, 1990. 256 с. 7. Л. Рабинер, Б. Гоулд. Теория и применение цифровой обработки сигналов. – М. , Мир, 1978, 848 с. 8. Дж. Прокис. Цифровая связь. – М. : Радио и связь, 2000, 797 с. 9. Д. Даджион, Р. Мерсеро. Цифровая обработка многмерных сигналов. – М. , Мир, 1988, 488 с. 10. Волков Л. Н. и др. Системы цифровой радиосвязи: базовые методы и характеристики. – М. : Эко-Трендз, 2005. 11. Галкин В. А. Цифровая мобильная радиосвязь. – М. : Горячая линия-Телеком, 2012, 592 с. 1

модели сигнала сигнал, сообщение, информация Сигнал ( «signum» — «знак» ), имеет широкий смысловой диапазон В соответствии с принятой традицией сигналом называют процесс изменения во времени физического состояния какого-либо объекта, служащий для отображения, регистрации и передачи сообщений. В практике человеческой деятельности сообщения неразрывно связаны с заключенной в них информацией. Круг вопросов, базирующихся на понятиях «сообщение» и «информация» , весьма широк. Он является объектом пристального внимания инженеров, математиков, лингвистов, философов. Мы не будем излагать связь, которая существует между физическим обликом сигнала и смыслом заключенного в нем сообщения. Также не будем обсуждаться вопрос о ценности информации, заключенной в сообщении и в конечном счете в сигнале. 2

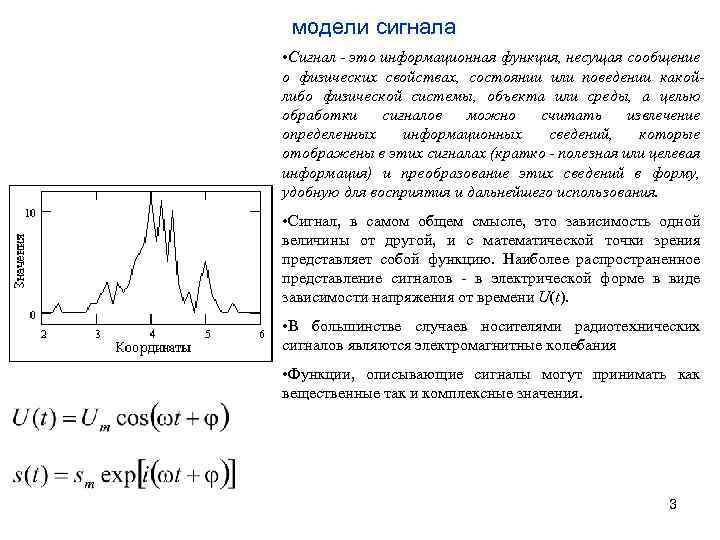модели сигнала • Сигнал - это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какойлибо физической системы, объекта или среды, а целью обработки сигналов можно считать извлечение определенных информационных сведений, которые отображены в этих сигналах (кратко - полезная или целевая информация) и преобразование этих сведений в форму, удобную для восприятия и дальнейшего использования. • Сигнал, в самом общем смысле, это зависимость одной величины от другой, и с математической точки зрения представляет собой функцию. Наиболее распространенное представление сигналов - в электрической форме в виде зависимости напряжения от времени U(t). • В большинстве случаев носителями радиотехнических сигналов являются электромагнитные колебания • Функции, описывающие сигналы могут принимать как вещественные так и комплексные значения. 3

модели сигнала Анализ сигналов Под "анализом" сигналов имеется в виду не только их чисто математические преобразования, но и получение на основе этих преобразований выводов о специфических особенностях соответствующих процессов и объектов. Например, ответ на казалось бы элементарный вопрос: в каком смысле можно говорить о величине сигнала, утверждая, что один сигнал значительно превосходит другой. Обычные цели анализа сигналов : - Определение или оценка числовых параметров сигналов (энергия, средняя мощность, среднее квадратическое значение и пр. ). - Разложение сигналов на элементарные составляющие для сравнения свойств различных сигналов. - Сравнение степени близости, "похожести", "родственности" различных сигналов, в том числе с определенными количественными оценками. Математический аппарат анализа сигналов весьма обширен, и широко применяется на практике во всех без исключения областях науки и техники. 4

модели сигнала Одномерные и многомерные сигналы Одномерный описывается одной функцией s(t) Многомерный описывается упорядоченной совокупностью функций {s 1(t); s 2(t); s 3(t); …. . }. Примеры Замечание 5

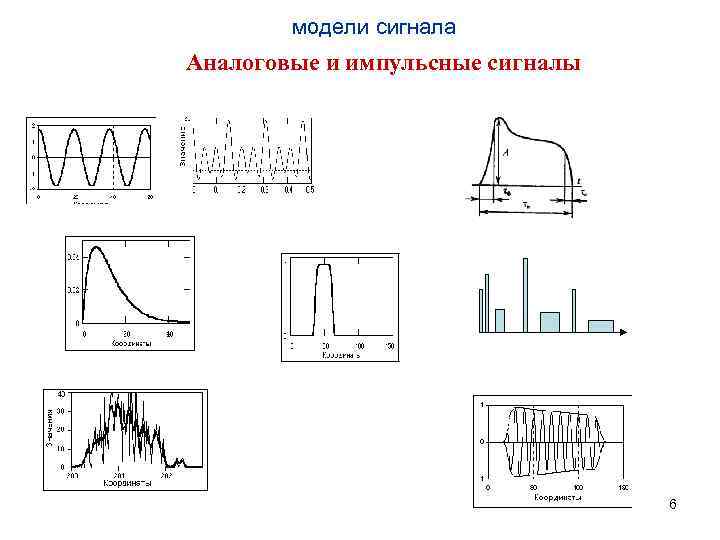модели сигнала Аналоговые и импульсные сигналы 6

модели сигнала Дискретные и цифровые сигналы 7

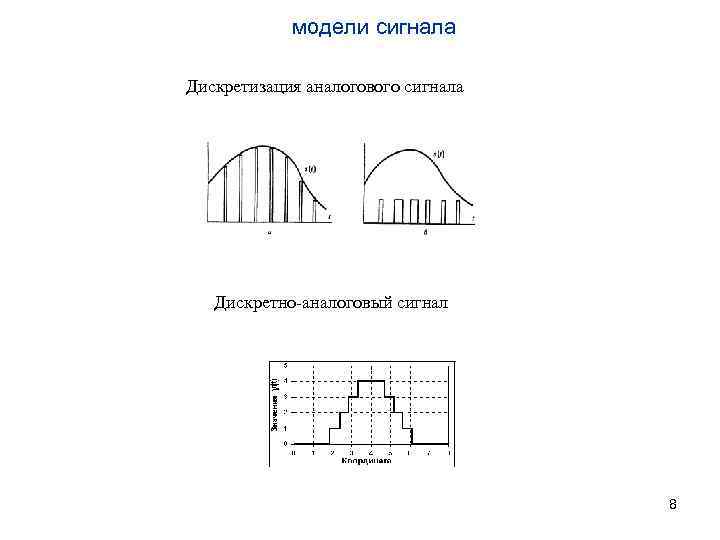модели сигнала Дискретизация аналогового сигнала Дискретно-аналоговый сигнал 8

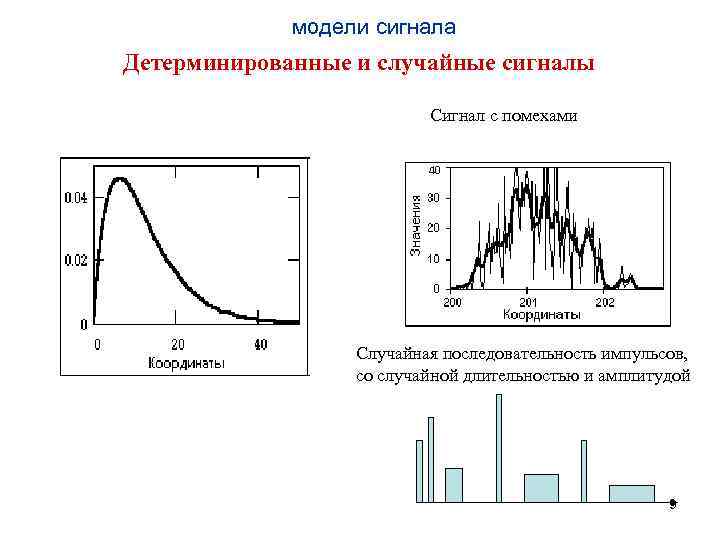модели сигнала Детерминированные и случайные сигналы Сигнал с помехами Случайная последовательность импульсов, со случайной длительностью и амплитудой 9

модели сигнала Динамическое представление сигналов Принцип динамического представления. Реальный сигнал приближенно представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. Если теперь устремить к нулю длительность отдельных элементарных сигналов, то, естественно, в пределе будет получено точное представление исходного сигнала. Два широкораспространенных способа в качестве элементарных сигналов используются ступенчатые функции, возникающие через равные промежутки времени , высота каждой ступеньки равна приращению сигнала на интервале времени . элементарными сигналами служат прямоугольные импульсы, непосредственно примыкающие друг к другу и образующие последовательност, вписанную в кривую или описанную вокруг 10 нее.

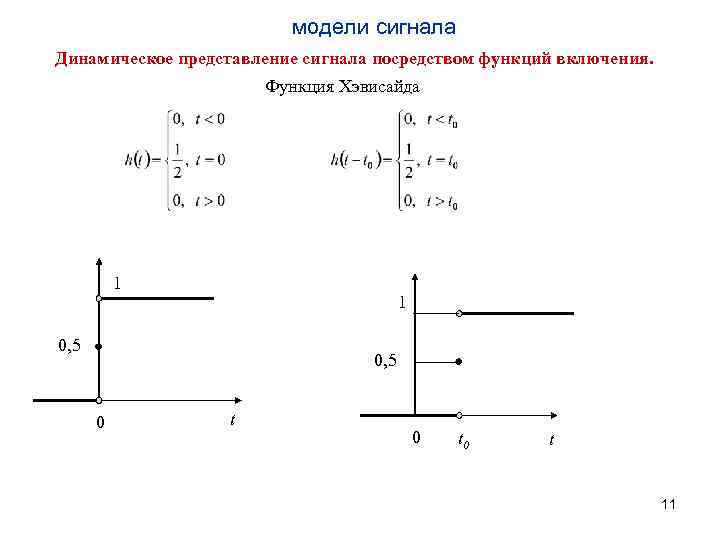модели сигнала Динамическое представление сигнала посредством функций включения. Функция Хэвисайда 1 1 0, 5 0 t 0 t 11

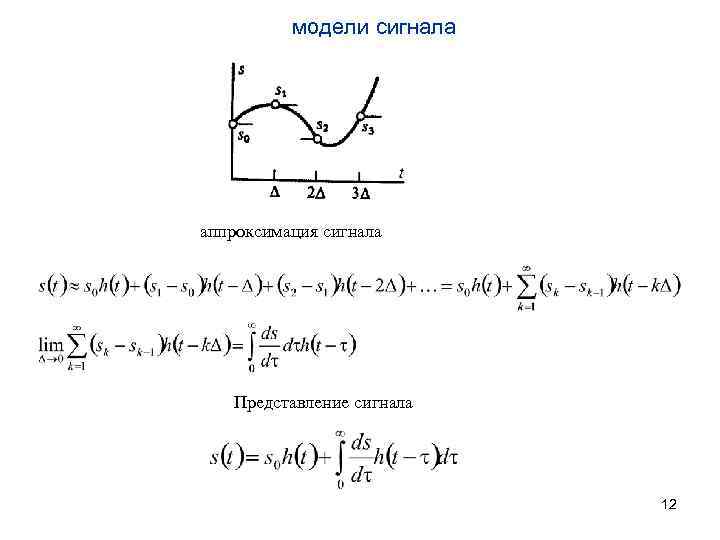модели сигнала аппроксимация сигнала Представление сигнала 12

модели сигнала Представление сигнала посредством -функций Функция Дирака - обобщенная функция Фильтрующее свойство Интуитивно должно быть Но тогда, что за интеграл в предыдущих формулах? 13

модели сигнала Импульс на k-ом отрезке Импульсная аппроксимация сигнала Импульсное представление сигнала 14

модели сигнала Свойства функции Дирака четность Обобщенное фильтрующее свойство Изменение масштаба Представление пределом последовательности функций sin Представление интегралом Фурье 15

модели сигнала Обобщенные функции, как математические модели сигналов В классической математике полагают, что функция f(t) должна принимать какие-то значения в каждой точке оси t. Однако рассмотренная -функция не вписывается в эти рамки - ее значение при t = 0 не определено вообще, хотя эта функция и имеет единичный интеграл. Очевидна необходимость расширить само понятие функции как математической модели сигнала. Современная математика преодолела эту трудность, введя принципиально новое понятие обобщенной функции. В основе идеи обобщенной функции лежит простое интуитивное соображение. Держа в руках и рассматривая какой-нибудь предмет, мы его поворачиваем, стремясь получить множество проекций этого объекта на всевозможные плоскости. Аналогом «проекции» исследуемой функции s(t) может служить, например, значение интеграла На множестве пробных финитных классических функций (t). Такой интеграл называют функционалом. 16

модели сигнала Этот интеграл линеен Если он еще и непрерывен, то говорят, что на множестве пробных функций (t) задана обобщенная функция f(t). Подчеркнем, что этот интеграл нужно понимать формально-аксиоматически, а не как предел соответствующих интегральных сумм, который в смысле определения обычного интеграла Римана может и не существовать. 17

модели сигнала Дифференцирование обобщенных функций Пример: производная функции Хэвисайда 18

модели сигнала 19

модели сигнала 20

модели сигнала Спасибо за внимание! 21