МОДЕЛИ ОПИСЫВАЕМЫЕ СИСТЕМАМИ ДВУХ АВТОНОМНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

МОДЕЛИ, ОПИСЫВАЕМЫЕ СИСТЕМАМИ ДВУХ АВТОНОМНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.

Основные понятия: • • • Фазовая плоскость. Фазовый портрет. Метод изоклин. Главные изоклины. Устойчивость стационарного состояния. Линейные системы. Типы особых точек: узел, седло, фокус, центр.

Типы устойчивости стационарного состояния Ляпунов Александр Михайлович (1857 -1918) - выдающийся русский математик, создал теорию устойчивости состояний равновесия и движения механических систем с конечным числом параметров. Работал также в области дифференциальных уравнений, гидродинамики, теории вероятностей.

Рассмотрим систему (1): P(x, y), Q(x, y)- непрерывные функции, определенные в некоторой области G евклидовой плоскости и имеющие в этой области непрерывные производные порядка не ниже первого.

Пусть в начальный момент времени t=t 0 координаты изображающей точки М 0(x(t 0), y(t 0)). В каждый следующий момент времени t изображающая точка будет смещаться в соответствии с изменениями значений переменных x(t), y(t). Совокупность точек М(x(t), y(t)) на фазовой плоскости, положение которых соответствует состояниям системы в процессе изменения во времени переменных x(t), y(t) согласно уравнениям (1), называется фазовой траекторией. Совокупность фазовых траекторий при различных начальных значениях переменных образует фазовый портрет системы.

Метод изоклин

Линии вдоль которых направление поля одинаково называются изоклинами. Точка пересечения всех изоклин называется особой точкой. Она соответствует стационарному состоянию системы (1) и определяется из условия Главные изоклины: dy/dx=0, P(x, y)=0 – изоклина горизонтальных касательных и dy/dx= , Q(x, y)=0 – изоклина вертикальных касательных.

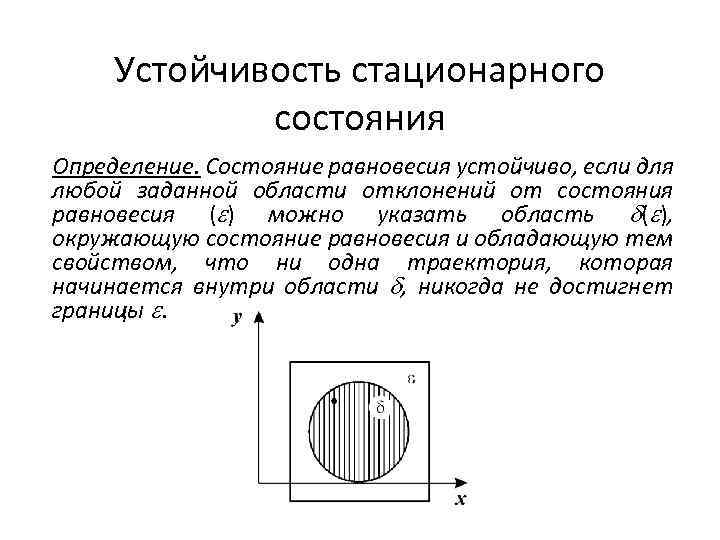Устойчивость стационарного состояния Определение. Состояние равновесия устойчиво, если для любой заданной области отклонений от состояния равновесия ( ) можно указать область ( ), окружающую состояние равновесия и обладающую тем свойством, что ни одна траектория, которая начинается внутри области , никогда не достигнет границы .

Линейные системы Типы поведения траекторий в окрестности стационарного состояния (2) (3) (4)

Рассмотрим систему в каноническом виде: 1) Корни λ 1, λ 2 – действительны и одного знака. Особая точка типа узел

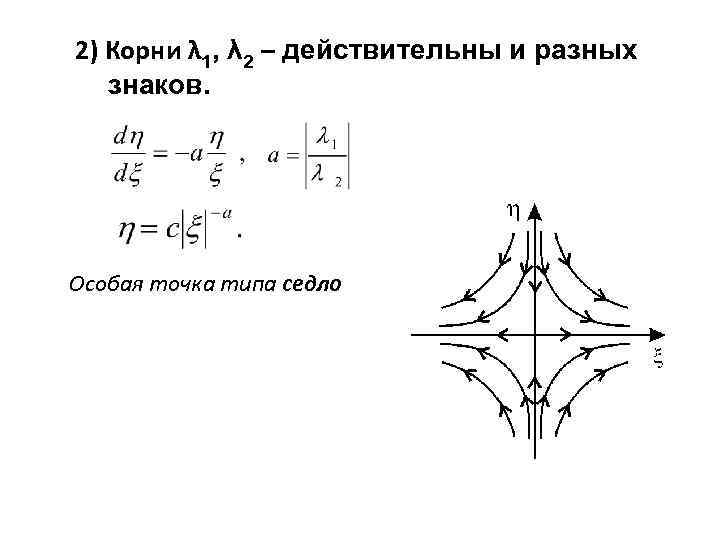2) Корни λ 1, λ 2 – действительны и разных знаков. Особая точка типа седло

Если ad-bc=0, то состояниями являются все точки прямой равновесия Остальные интегральные кривые представляют собой семейство параллельных прямых с угловым коэффициентом Фазовый портрет, когда один из корней характеристического уравнения равен нулю, а другой – отрицательный

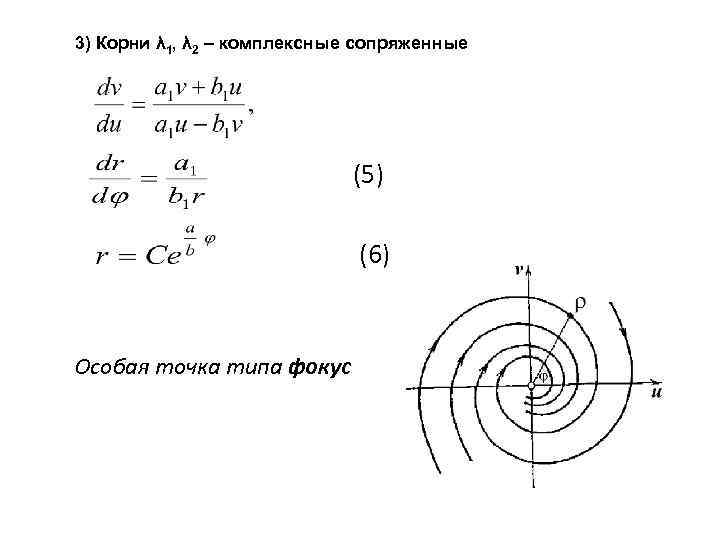3) Корни λ 1, λ 2 – комплексные сопряженные (5) (6) Особая точка типа фокус

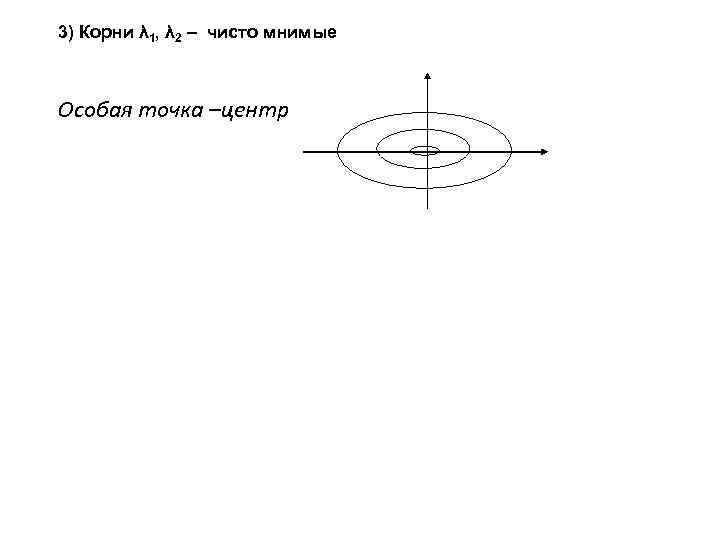3) Корни λ 1, λ 2 – чисто мнимые Особая точка –центр

Типы поведения фазовых траекторий в окрестности стационарного состояния для линейной системы

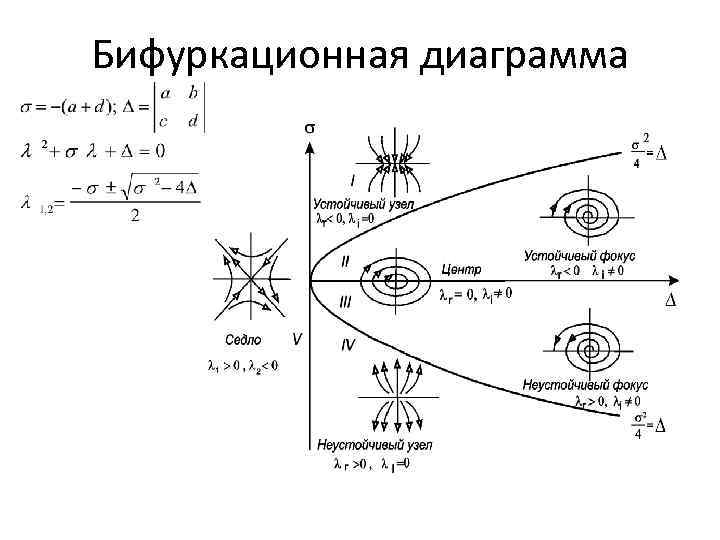Бифуркационная диаграмма

Пример. Система линейных химических реакций

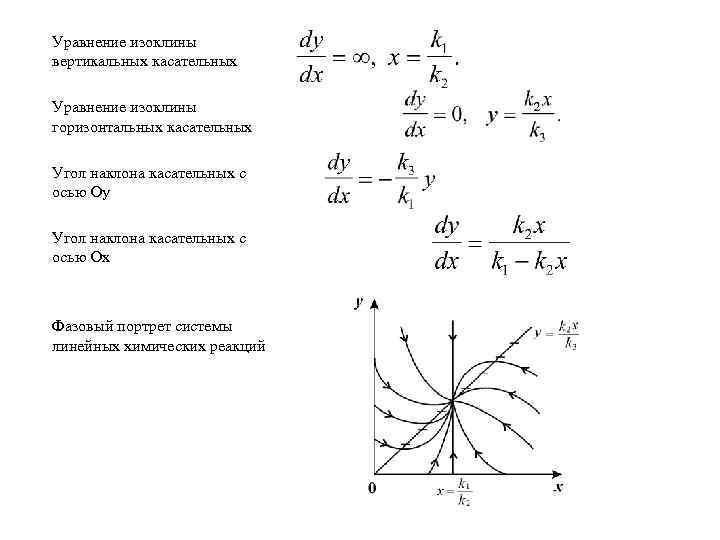Уравнение изоклины вертикальных касательных Уравнение изоклины горизонтальных касательных Угол наклона касательных с осью Оу Угол наклона касательных с осью Ох Фазовый портрет системы линейных химических реакций