Модели экономического роста Актуальность темы Сущность

Модели экономического роста • Актуальность темы • Сущность эконом. роста • Основные вопросы теории • • • роста Моделирование роста Модель Лукаса Базовые положения модели Модель Солоу Диаграмма и фазовая диаграмма модели Список литературы

Актуальность темы • Повышение качества жизни • Решение глобальных проблем: - Рост населения и ограниченность ресурсов - Бедность, голод, неграмотность - Войны, конфликты - Экология, болезни Чтобы все это решить достаточно ускорить рост.

Основные вопросы теории роста. • • Каковы источники экономического роста? В чем причина различий в доходах между странами? • • Ответив на эти вопросы, мы научимся управлять экономическим ростом, а значит решать большинство проблем, с которыми сегодня сталкиваемся Роберт Лукас: – «Однажды задумавшись над этими вопросами, экономисту сложно думать о чем-нибудь еще» • • Роберт Эмерсон Лукас, младший Дата рождения: 15 сентября 1937) Место рождения: Якима, шт. Вашингтон, США Научная сфера: экономика Автор модели «Лукаса-Ромера» , Вклад в теории нейтральности денег и рациональных ожиданий Награды и премии Нобелевская премия по экономике (1995)

Моделирование роста • Логика (любого) моделирования – Поставить вопрос • Основные вопросы теории роста – Задать предпосылки (обычно самая сложная часть) – Вывести результат (обычно самая легкая часть) – Отвечает ли модель на вопрос, который был задан? – Проверить результат эмпирически… – Проверить предпосылки… найти ошибку – Построить другую модель. . .

Эндогенный экономический рост. Модель Лукаса • Модель Лукаса что это? • Базовые положения о модели. • Решения об образовании. • Общая задача модели. • Конкурентный рост.

Базовые положения модели 1) Общий объем человеческого капитала H=h*L L=const 2) Сектор конечной продукции 3)Накопление физического капиатала К=Y-C 4) Продуктом производства сектора образования является прирост индивидуального уровня чел капитала

Решения об образовании 1) Доход 2) Нормирование человеческого капитала и зар. платы к 1 получаем Условие максимум будет следующим

• Сокращая интеграл и решая его получаем • Общее решение задачи максимизации дохода индивидуума будет выглядеть следующим образом

Общая задача модели • Общую задачу модели можно определить, как задачу максимизации полезности домашним хозяйством с бесконечным временным горизонтом. При оптимальном выборе уровня потребления С, времени обучения U и заданных начальных объемах физического и человеческого капиталов Система будет выглядеть следующим образом

Математическое отражение задачи

Конкурентный рост • Конкуренция приводит к тому, что предельная производительность в секторе равна факторным издержкам • Производственная функция и уравнения заработной платы выглядят след образом

Модель Солоу. üПервая и самая важная неоклассическая модель роста üРеалистично описывает долгосрочные тенденции в развитых странах üЗаложила основу современной теории роста üМодификации модели Солоу используются при разработке экономической политики многих стран и стратегий международных компаний

Роберт Солоу • Ph. D. , Harvard • Emeritus • • Professor of Economics, MIT Nobel Prize, 1987 http: //en. wikipedi a. org/wiki/Robert _Solow

Модель Солоу. • Модель изучает динамику • • Y — выпуск продукции A — технический прогресс K — объем используемого капитала L — затраты живого труда • накопления капитала Модель экзогенного роста Базовая модель для анализа роста Базовые предпосылки: основаны на производственной функции Время не входит прямо в производственную функцию Для заданных K и L выпуск со временем увеличивается только за счет технического прогресса

Динамика модели Это дифференциальное уравнение. Наша цель–найти стационарное решение и изучить динамику системы около него Поэтому приравняем Получим Левая часть возрастает по k с убывающим темпом, так как Правая часть возрастает линейно Сделав дополнительные предпосылки (условия Инады) , решим уравнение графически

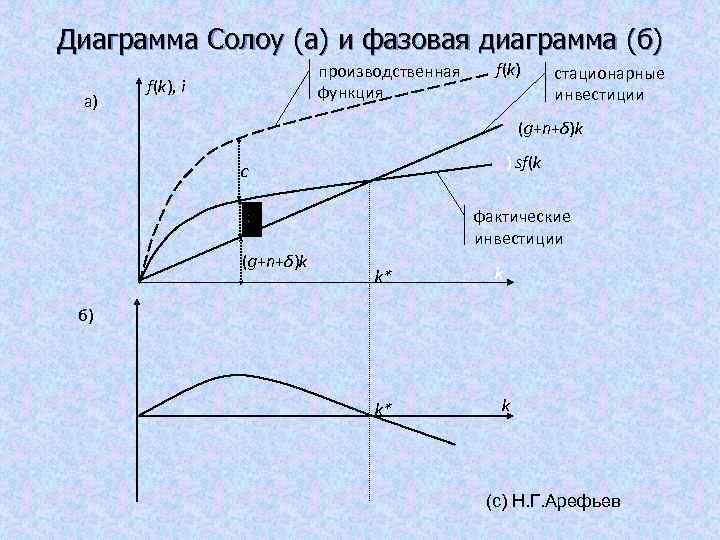Диаграмма Солоу (а) и фазовая диаграмма (б) а) производственная функция f(k), i f(k) стационарные инвестиции (g+n+δ)k ) sf(k c фактические инвестиции (g+n+δ)k k* k б) k* k (с) Н. Г. Арефьев

Используемая литература – – – – – Ромер, главы 1 и 3 Бланшар, главы 10 -13 Mankiw, Macroeconomics, ch. 7 -8 Ю. В. Шараев. Теория экономического роста, 2006 В. М. Полтерович, лекции D. Acemoglu. Introduction to modern economic growth, 2009, ch. 2, 3, 11, 14 P. Aghion, P. Howitt. Endogenous Growth Theory, 1999, ch. 1 -2 P. Aghion, P. Howitt. The Economics of Growth, 2009, ch. 1 -2 R. Lucas, Ideas and Growth (Economica, 2009)