fd83c15889eaa5bac57947c22625c9c1.ppt
- Количество слайдов: 38

Modelarea matematica a proceselor biologice - Curs -

Structura cursului: Cap. 1: Introducere in modelarea numerica a proceselor biologice Cap. 2: Ecuatii de transport Cap. 3: Difuzia. Conductia termica. Cap. 4: Microcurgeri

Cap. 5: Micropicaturi Cap. 6: Transportul speciilor biochimice Cap. 7: Reactii biochimice Cap. 8: Curgerea si transportul de masa in domenii variabile Cap. 9: Transportul in camp magnetic Cap. 10: Transportul in camp electric

BIBLIOGRAFIE: 1) Friedman M. H. 2008, Principles and models of biological transport; Springer. 2) Kojic M, et al. 2008, Computer modeling in bioengineering; Wiley & Sons. 3) Berthier J. , Silberzan P. 2005, Microfluidics for Biotechnology; Artech House, Boston/London. 4) Alberts B, et al. 2002 Molecular biology of the cell; 4 th ed. New York, Garland Science. 5) Perthame B. 2007 Transport equations in biology; Birkhauser Verlag. 6) Dym C. 2004 Principles of mathematical modelling; Academic Press.

A. Neculae: Modelarea matematica a proceselor biologice (Curs) Capitolul 6: Transportul speciilor biochimice 6. 1 Consideratii generale 6. 2 Ecuatia de advectie-difuzie 6. 3 Calculul traiectoriilor 6. 4 Separarea/Purificarea bioparticulelor 6. 5 Simularea numerica a proceselor de advectie-difuzie (seminar)

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 1 Cosideratii generale Biotehnologiile implica transportul selectiv al elementelor biologice Situatii intalnite, in functie de gradul de selectivitate [3]:
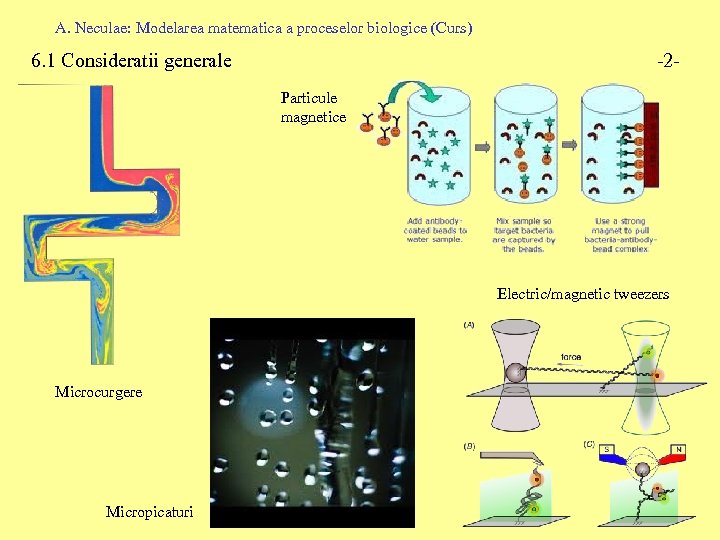
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 1 Consideratii generale -2 Particule magnetice Electric/magnetic tweezers Microcurgere Micropicaturi

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie (transport convectiv) Forma generala a ecuatiei de advectie-difuzie: Daca S = 0: In coordonate carteziene: Daca D = ct:

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie Transportul in absenta difuziei: -2 -
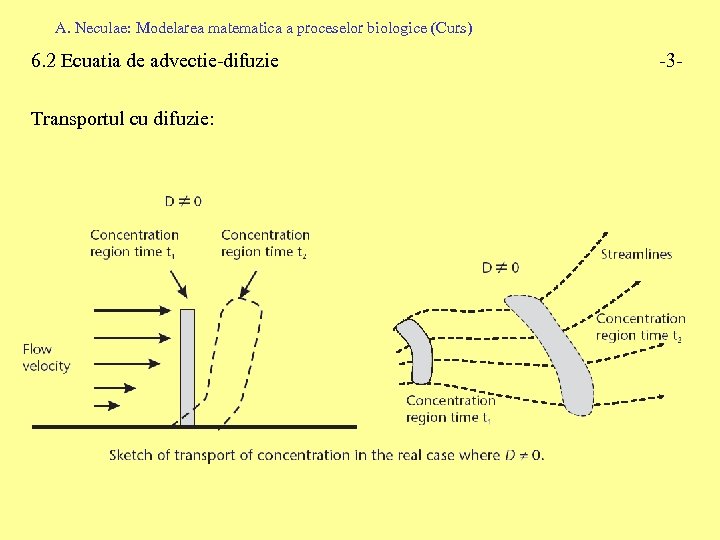
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie Transportul cu difuzie: -3 -
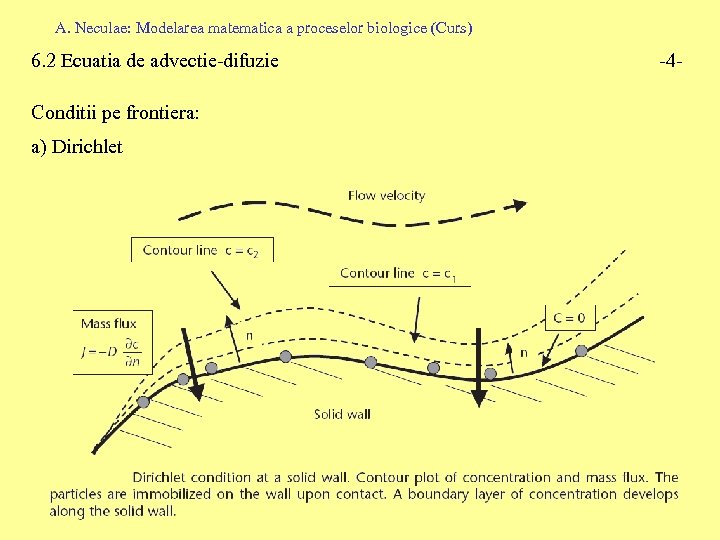
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie Conditii pe frontiera: a) Dirichlet -4 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie Conditii pe frontiera: b) Neumann omogen -5 -
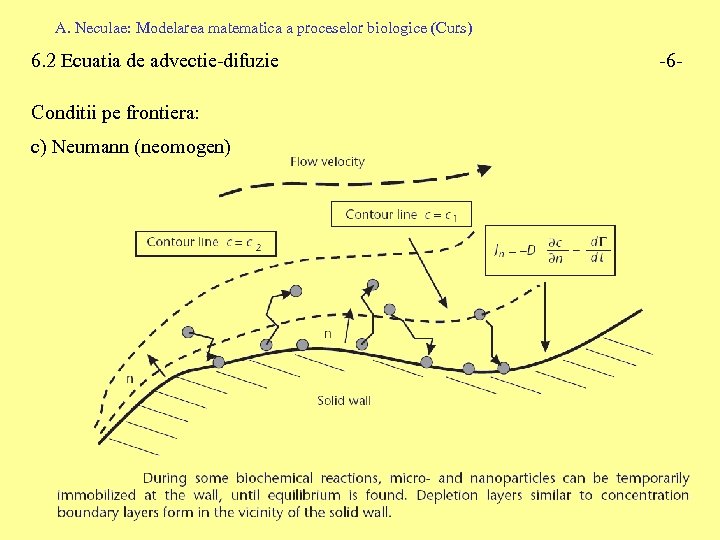
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie Conditii pe frontiera: c) Neumann (neomogen) -6 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie -7 - Cuplajul cu hidrodinamica: a) Cazul general: b) Curgere stationara, fluid incompresibil: c) Aproximatia Stokes:

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie -8 - Variatia proprietatilor fizice cu concentratia: Fractia volumica a particulelor: a) Vascozitatea aparenta a unei solutii: pentru solutii diluate: pentru particule sferice:

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie -9 - b) Coeficientul de difuzie: Relatia Einstein: - variatia relativa a coeficientului de difuzie: c) Densitatea: Densitatea amestecului lichid-particule: - variatia relativa a densitatii:

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie Ecuatii de transport cuplate Sistemul de ecuatii de transport in aproximatia Stokes: impreuna cu relatiile constitutive: -10 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 2 Ecuatia de advectie-difuzie Ecuatii adimensionalizate. Numarul Peclet. Ecuatia de advectie-difuzie fara termen sursa in coordonate carteziene: Relatii de adimensionalizare: Ecuatia de advectie-difuzie adimensionalizata: Numarul Peclet: -11 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 3 Calculul traiectoriilor In stabilirea ecuatiei de advectie-difuzie, greutatea particulelor a fost neglijata. In cazul particulor mari (grele) procesul de sedimantare nu mai poate fi neglijat (miscarea Browniana devine neglijabila) si gravitatia trebuie luata in considerare. Miscarea unei particule este guvernata de legea lui Newton: Forta de rezistenta hidrodinamica: Forta gravitationala:

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 3 Calculul traiectoriilor Ecuatia pentru viteza particulei devine: In cazul 2 D, se scrie pe componente: -2 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 3 Calculul traiectoriilor Facand notatiile: sistemul de ecuatii devine: Solutiile analitice ale acestuia sunt: -3 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 3 Calculul traiectoriilor -4 - Ecuatiile pentru coordonate: Daca presupunem o curgere Poiseuille a fluidului si viteza initiala a particulei nula obtinem relatiile: si ecuatia traiectoriei: unde este pozitia initiala a particulei.

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 4 Separarea/Purificarea bioparticulelor Separarea/purificarea bioparticulelor este necesara intr-un numar important de aplicatii: - purificarea proteinelor - separarea secventelor ADN dupa lungime - etc. . Principalele tehnici utilizate: - separarea in camp de curgere (Field Flow Fractionation - FFF) - coloanele cromatografice(chromatography columns)

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 4 Separarea/Purificarea bioparticulelor -2 - a) Separare in camp de curgere (Field Flow Fractionation - FFF): Rezultatul separarii:
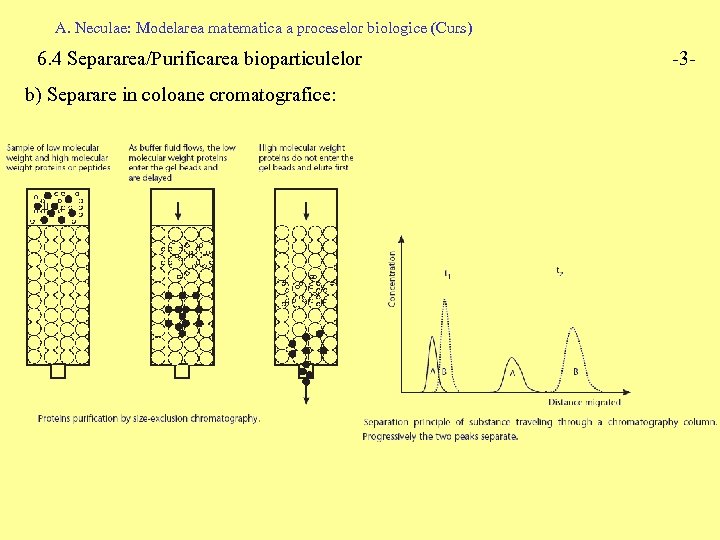
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 4 Separarea/Purificarea bioparticulelor b) Separare in coloane cromatografice: -3 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 4 Separarea/Purificarea bioparticulelor Detectia cu spectrometru de masa: -4 -
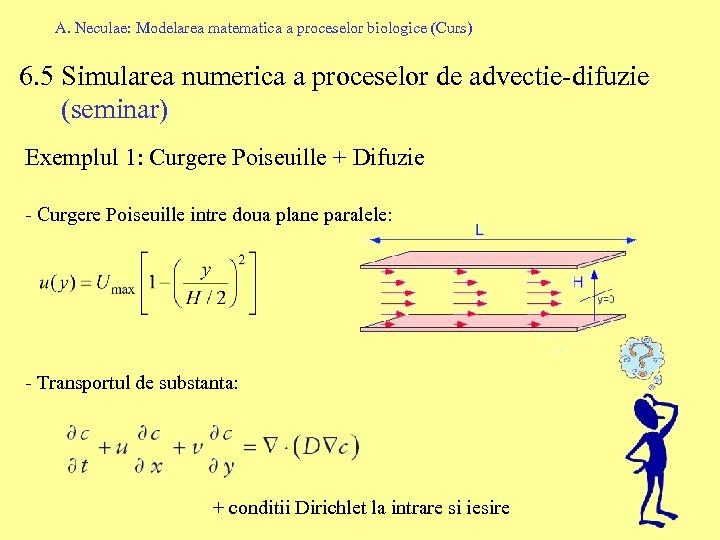
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie (seminar) Exemplul 1: Curgere Poiseuille + Difuzie - Curgere Poiseuille intre doua plane paralele: - Transportul de substanta: + conditii Dirichlet la intrare si iesire

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie // // Program curgere Poiseuille + transport de substanta // real A=1. ; real H=10. ; real umax=1. ; real D=1. ; border a (t=0, H) {x=t; y=0; label=1; }; border b (t=0, A) {x=H; y=t; label=2; }; border c (t=H, 0) {x=t; y=A; label=3; }; border d (t=A, 0) {x=0; y=t; label=4; }; mesh dom=buildmesh(a(100) +b(10) +c(100) +d(10)); plot (dom, wait=1); fespace Vh(dom, P 2); fespace Ph(dom, P 1); Vh u, v, psit, C, Ct, Cold; Ph p, pth; int i=0; real dt=0. 01; -2 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie problem streamlines(psi, psit)= int 2 d(dom, qforder=5)(dx(psi)*dx(psit)+dy(psi)*dy(psit)) +int 2 d(dom, qforder=5)(-psit*(dy(u)-dx(v))) + on(1, psi=0); problem Conc(C, Ct)= int 2 d(dom, qforder=5)( (1. /dt)*C*Ct+ u*dx(C)*Ct+v*dy(C)*Ct+D*(dx(C)*dx(Ct)+dy(C)*dy(Ct))) +int 2 d(dom, qforder=5)(-(1. /dt)*Cold*Ct) + on(4, C=1)+ on(2, C=0); real[int] yy(201), yyu(201); u=umax*4*y*(1 -y); Cold=0; {ofstream file("u. txt"); for (int jj=0; jj<=200; jj++) {x=H/2. ; y=(jj*0. 005); yy[jj]=y; yyu[jj]=u; file << yyu[jj] << " "<< yy[jj] << endl; }} -3 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie for (i=0; i<=500; i++) { streamlines; if (!(i % 500)) plot(psi, wait=0, bw=0, value=1, nbiso=10, ps="psi_"+i*dt+". eps"); Conc; if (!(i % 50)) plot(C, wait=0, bw=0, value=1, nbiso=10, ps="C_"+i*dt+". eps"); Cold=C; if (!(i % 100)) { ofstream file("C_050 H"+i*dt+". txt"); for (int jj=0; jj<=200; jj++) {x=0. 5*H. ; y=(jj*0. 005); yy[jj]=y; yyu[jj]=C; file << yyu[jj] << " "<< yy[jj] << endl; }} }; -4 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie -5 -
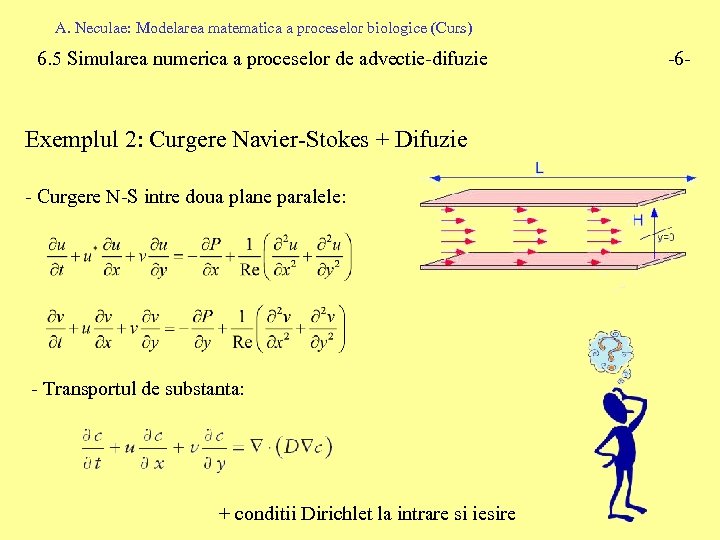
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie Exemplul 2: Curgere Navier-Stokes + Difuzie - Curgere N-S intre doua plane paralele: - Transportul de substanta: + conditii Dirichlet la intrare si iesire -6 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie // // Program curgere Navier-Stokes --> Poiseuille + transport de substanta // real A=1. ; real H=10. ; border a (t=0, H) {x=t; y=0; label=1; }; border b (t=0, A) {x=H; y=t; label=2; }; border c (t=H, 0) {x=t; y=A; label=3; }; border d (t=A, 0) {x=0; y=t; label=4; }; mesh dom=buildmesh(a(100) +b(20) +c(100) +d(20)); plot (dom, wait=1); fespace Vh(dom, P 2); fespace Ph(dom, P 1); Vh u, v, ut, vt, uth, up, vp, psit, C, Ct, Cold; Ph p, pth; int i=0; real Re=10. ; real dt=0. 01; real D=1. ; -7 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie problem NS(u, v, p, ut, vt, pt, solver=Crout, eps=1. e-8, init=i)= int 2 d(dom, qforder=5)((1. /dt)*(u*ut+v*vt)+ (1/Re)*(dx(u)*dx(ut)+dy(u)*dy(ut)+dx(v)*dx(vt)+dy(v)*dy(vt))+ p*pt*(0. 00000001)+dx(p)*ut+dy(p)*vt+dx(u)*pt+dy(v)*pt) +int 2 d(dom, qforder=5)(-(1. /dt)*convect([up, vp], -dt, up)*ut -(1. /dt)*convect([up, vp], -dt, vp)*vt) + on(1, 3, u=0, v=0)+ on(4, p=8*H/Re)+ on(2, p=0); problem streamlines(psi, psit)= int 2 d(dom, qforder=5)(dx(psi)*dx(psit)+dy(psi)*dy(psit)) +int 2 d(dom, qforder=5)(-psit*(dy(u)-dx(v))) + on(1, psi=0); problem Conc(C, Ct)= int 2 d(dom, qforder=5)((1. /dt)*C*Ct+u*dx(C)*Ct+v*dy(C)*Ct +D*(dx(C)*dx(Ct)+dy(C)*dy(Ct))) +int 2 d(dom, qforder=5)(-(1. /dt)*Cold*Ct) + on(4, C=1)+ on(2, C=0); real[int] yy(201), yyu(201); uth=4*y*(1 -y); u=0; v=0; p=0; Cold=0; -8 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie for (i=0; i<=500; i++) { up=u; vp=v; NS; streamlines; if (!(i % 100)) plot(psi, wait=0, bw=0, value=1, nbiso=10, ps="psi_"+i*dt+". eps"); Conc; if (!(i % 100)) plot(C, wait=0, bw=0, value=1, nbiso=10, ps="C_"+i*dt+". eps"); Cold=C; if (!(i % 50)) { ofstream file("u_"+i*dt+". txt"); for (int jj=0; jj<=200; jj++) {x=H/2. ; y=(jj*0. 005); yy[jj]=y; yyu[jj]=u; file << yyu[jj] << " "<< yy[jj] << endl; }} -9 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie if (!(i % 100)) { ofstream file("C_000 H_"+i*dt+". txt"); for (int jj=0; jj<=200; jj++) {x=0. ; y=(jj*0. 005); yy[jj]=y; yyu[jj]=C; file << yyu[jj] << " "<< yy[jj] << endl; }} if (!(i % 100)) { ofstream file("C_050 H_"+i*dt+". txt"); for (int jj=0; jj<=200; jj++) {x=0. 5*H; y=(jj*0. 005); yy[jj]=y; yyu[jj]=C; file << yyu[jj] << " "<< yy[jj] << endl; }} }; -10 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie -11 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 6. 5 Simularea numerica a proceselor de advectie-difuzie Studiati efectul vitezei de curgere si coeficientului de difuzie asupra concentratiei! -12 -
fd83c15889eaa5bac57947c22625c9c1.ppt