Modelarea matematica a proceselor biologice — Curs —

Modelarea matematica a proceselor biologice - Curs -

Structura cursului: Cap. 1: Introducere in modelarea numerica a proceselor biologice Cap. 2: Ecuatii de transport Cap. 3: Difuzia. Conductia termica. Cap. 4: Microcurgeri

Cap. 5: Micropicaturi Cap. 6: Transportul speciilor biochimice Cap. 7: Reactii biochimice Cap. 8: Curgerea si transportul de masa in domenii variabile Cap. 9: Transportul in camp magnetic Cap. 10: Transportul in camp electric

BIBLIOGRAFIE: 1) Friedman M. H. 2008, Principles and models of biological transport; Springer. 2) Kojic M, et al. 2008, Computer modeling in bioengineering; Wiley & Sons. 3) Berthier J. , Silberzan P. 2005, Microfluidics for Biotechnology; Artech House, Boston/London. 4) Alberts B, et al. 2002 Molecular biology of the cell; 4 th ed. New York, Garland Science. 5) Perthame B. 2007 Transport equations in biology; Birkhauser Verlag. 6) Dym C. 2004 Principles of mathematical modelling; Academic Press.

A. Neculae: Modelarea matematica a proceselor biologice (Curs) Capitolul 4: Microcurgeri 4. 1 De la curgeri continue la picaturi 4. 2 Curgerea monofazica 4. 2. 1 Ecuatia Navier-Stokes 4. 2. 2 Ecuatia Stokes 4. 2. 3 Ecuatia Hagen-Poiseuille 4. 2. 4 Aproximatia Bernoulli 4. 3 Curgerea multifazica 4. 4 Simularea numerica a microcurgerilor (seminar)

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 1 De la curgeri continue la picaturi - elementele biologice (molecule, celule, etc. ) sunt aproape intotdeauna transportate de catre un fluid purtator (de regula un lichid si foarte rar un gaz) - de obicei discutam despre microcurgeri in canale si tuburi capilare, in care fluidul se deplaseaza sub actiunea presiunii (produsa de o siringa sau o micropompa) sau a fortelor electrice (curgere electro-osmotica) - Microcurgerea poate fi: - continua monofazica multifazica (bifazica, etc…) - digitala (picaturi manipulate individual)

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 1 De la curgeri continue la picaturi Exemple de microcurgeri [3]: -2 -

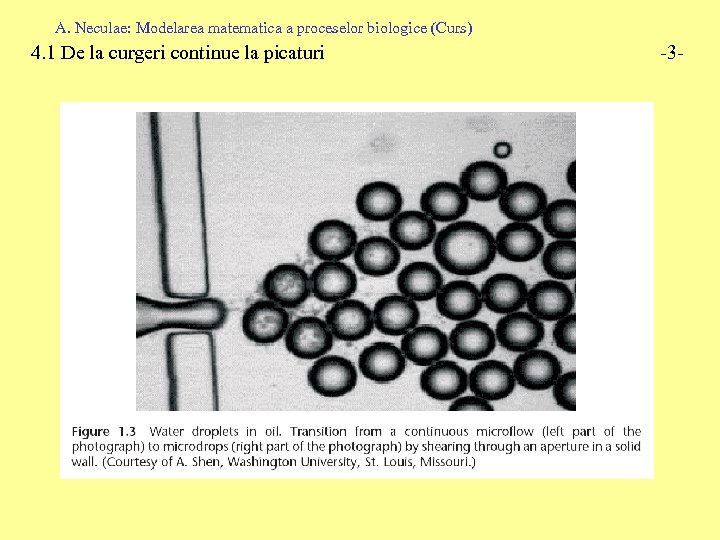
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 1 De la curgeri continue la picaturi -3 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 1 De la curgeri continue la picaturi -4 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica Ecuatii care guverneaza curgerea monofazica (au la baza ipoteza continuului): - Ecuatia de continuitate (conservarea masei) - Ecuatia de miscare (conservarea impulsului) - ecuatia Navier–Stokes - ecuatia Stokes - curgerea Hagen-Poiseuille - aproximatia Bernoulli - Ecuatia energiei (conservarea energiei)

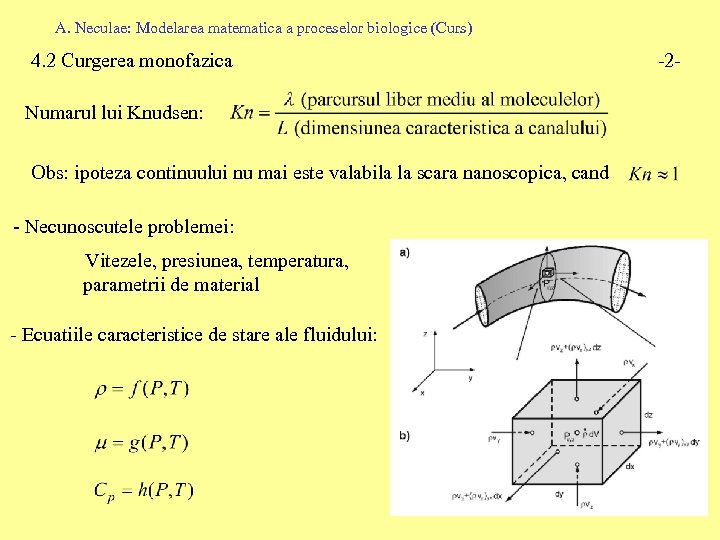
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica Numarul lui Knudsen: Obs: ipoteza continuului nu mai este valabila la scara nanoscopica, cand - Necunoscutele problemei: Vitezele, presiunea, temperatura, parametrii de material - Ecuatiile caracteristice de stare ale fluidului: -2 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica 4. 2. 1 Ecuatia Navier-Stokes: a) Ecuatia de continuitate (conservarea masei) - daca mediul este incompresibil: - in coordonate carteziene: - in coordonate cilindrice: -3 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica b) Ecuatia Navier-Stokes (conservarea impulsului) c) Ecuatia energiei (conservarea energiei ) -4 -

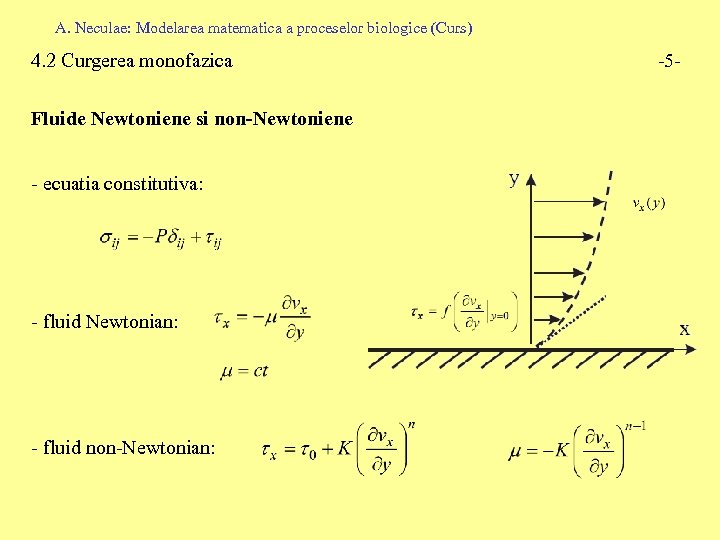
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica Fluide Newtoniene si non-Newtoniene - ecuatia constitutiva: - fluid Newtonian: - fluid non-Newtonian: -5 -

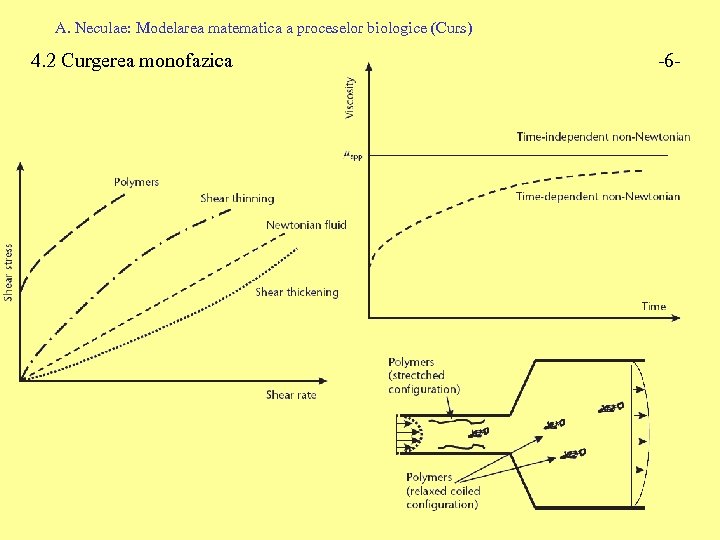
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica -6 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica Curgere laminara - fortele de vascozitate domina fortele de inertie - liniile de curgere sunt, cel putin la nivel local, paralele Obs: in caz contrar vorbim despre turbulenta! Numarul lui Reynolds: Regim laminar: -7 -

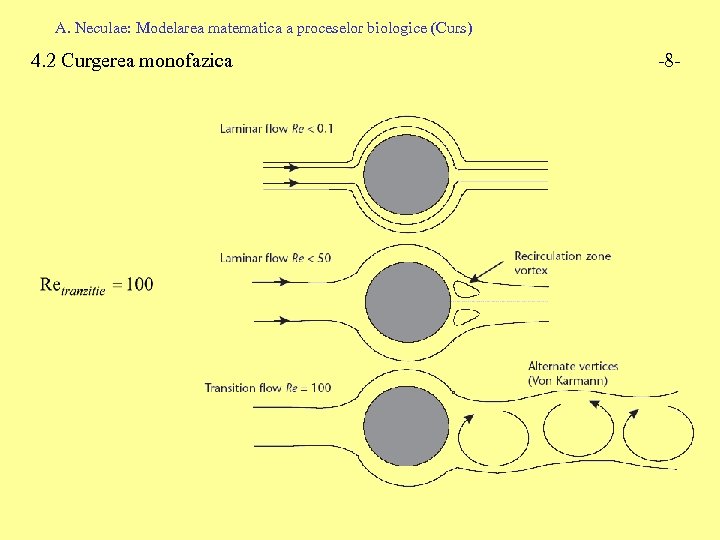
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica -8 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica Ecuatia N-S, cazul 2 D: Adimensionalizare: Ecuatii adimensionalizate: -9 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica 4. 2. 2 Ecuatia Stokes: - este valabila in cazul curgerii stationare lente, cand termenii inertiali devin neglijabili; Pentru o geometrie carteziana 2 D: Daca forta externa este gravitatia: -10 -

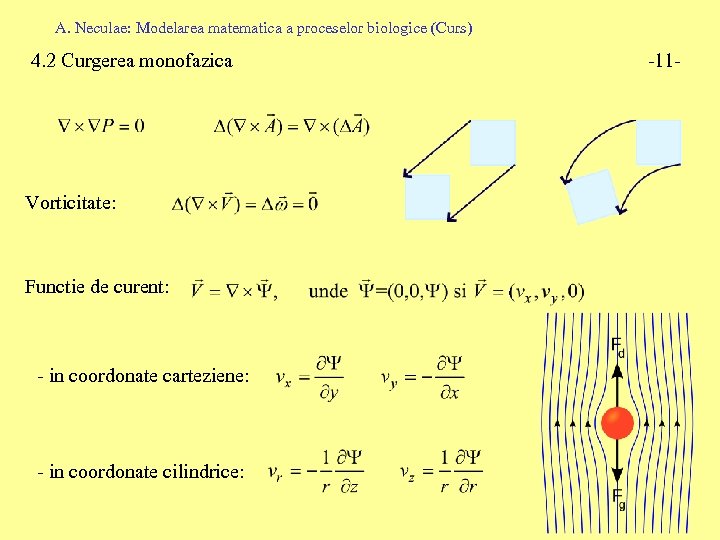
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica Vorticitate: Functie de curent: - in coordonate carteziene: - in coordonate cilindrice: -11 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica 4. 2. 3 Ecuatia Hagen-Poiseuille: - intr-un tub cilindric: - Curgere indusa de un gradient de presiune: -12 -

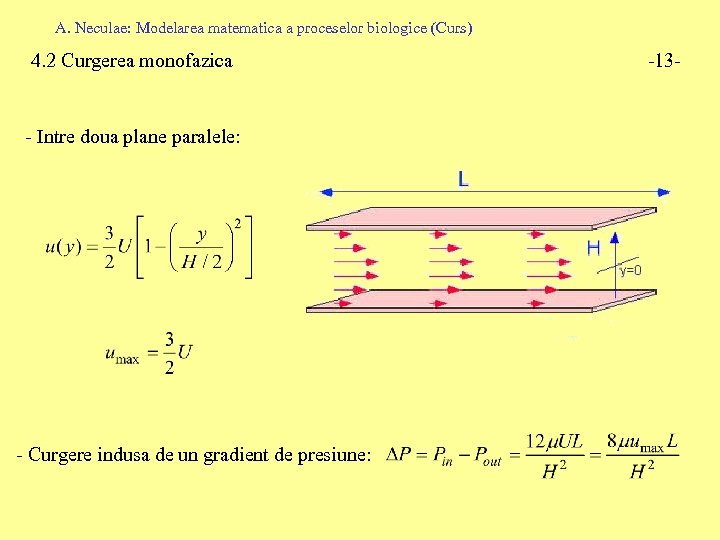
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica - Intre doua plane paralele: - Curgere indusa de un gradient de presiune: -13 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica -14 - 4. 2. 4 Aproximatia Bernoulli: - Ipoteze de lucru: problema unidimensionala, fluid perfect - Notatii :

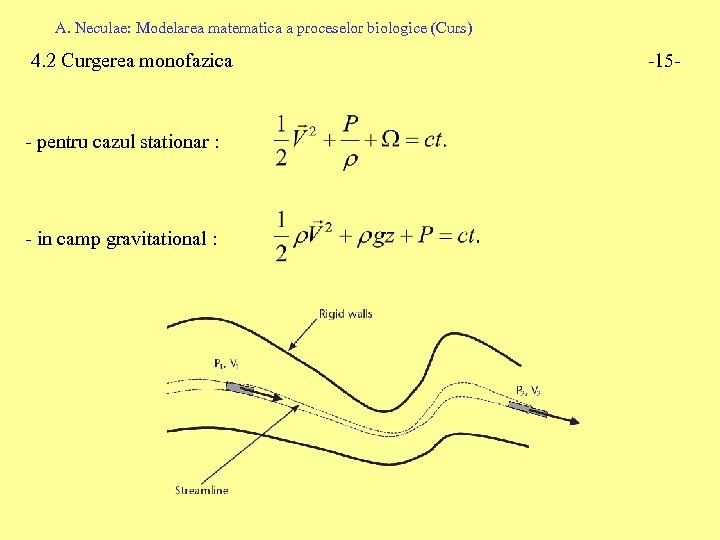
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 2 Curgerea monofazica - pentru cazul stationar : - in camp gravitational : -15 -

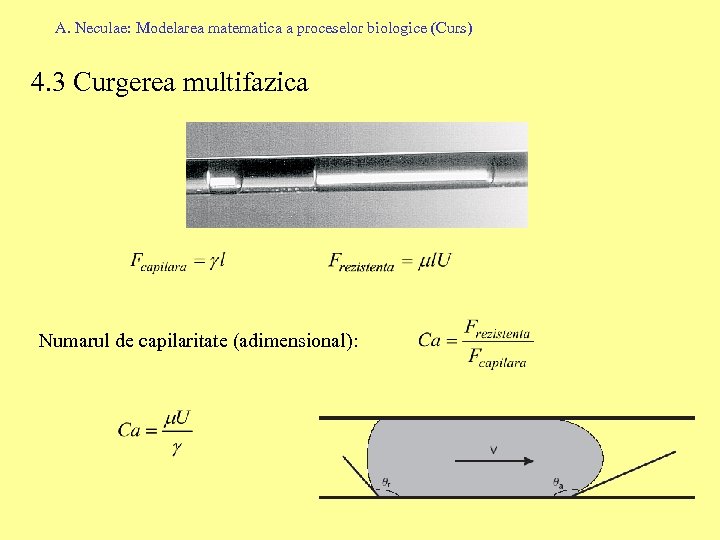
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 3 Curgerea multifazica Numarul de capilaritate (adimensional):

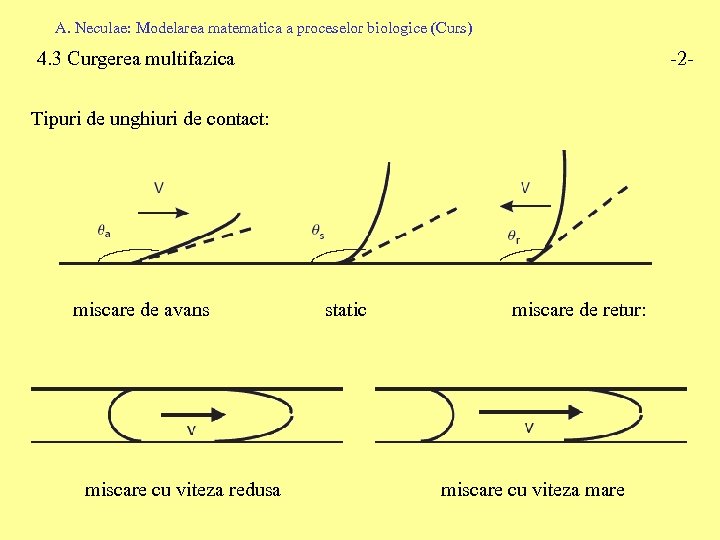
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 3 Curgerea multifazica -2 - Tipuri de unghiuri de contact: miscare de avans miscare cu viteza redusa static miscare de retur: miscare cu viteza mare

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcurgerilor (seminar) Exemple practice 1. Microcamera cu deflector:

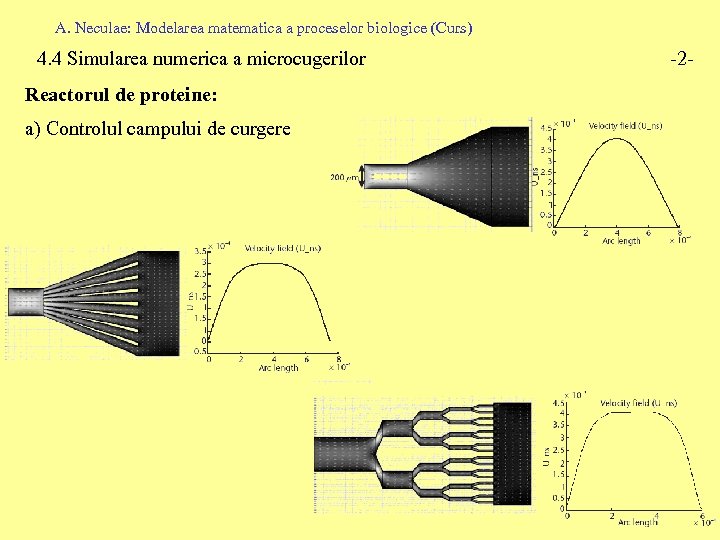
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor Reactorul de proteine: a) Controlul campului de curgere -2 -

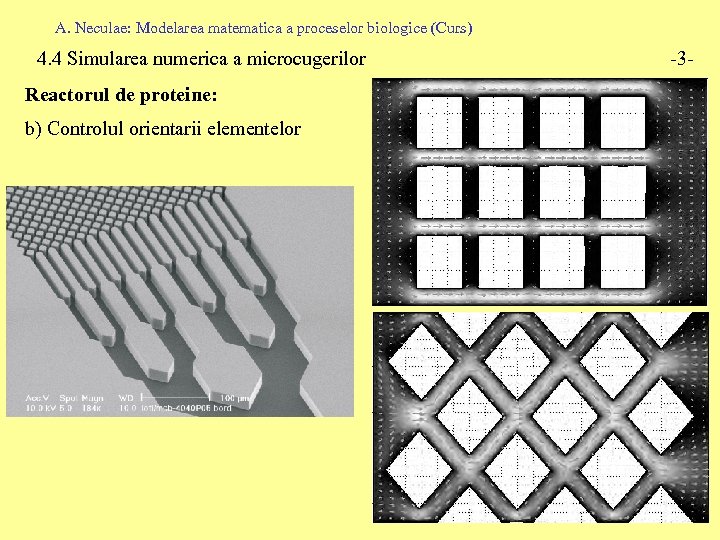
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor Reactorul de proteine: b) Controlul orientarii elementelor -3 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor Exercitiul 1: Curgerea Poiseuille intre doua plane cu conditii Dirichlet in viteza pe frontierele 1 si 3, respectiv in presiune pe frontierele 2 si 4 Solutie analitica: -4 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor real A=1. ; real H=10. ; int i=0; real Re=10. ; real dt=0. 01; border a (t=0, H) {x=t; y=0; label=1; }; border b (t=0, A) {x=H; y=t; label=2; }; border c (t=H, 0) {x=t; y=A; label=3; }; border d (t=A, 0) {x=0; y=t; label=4; }; mesh dom=buildmesh(a(100) +b(20) +c(100) +d(20)); plot (dom, wait=1); fespace Vh(dom, P 2); fespace Ph(dom, P 1); Vh u, v, ut, vt, uth, psit, up, vp; Ph p, pt; problem NS(u, v, p, ut, vt, pt, solver=Crout, eps=1. e-8, init=i)= int 2 d(dom, qforder=5)((1. /dt)*(u*ut+v*vt)+ (1/Re)*(dx(u)*dx(ut)+dy(u)*dy(ut)+ dx(v)*dx(vt)+dy(v)*dy(vt))+ p*pt*(0. 00000001)+ dx(p)*ut+dy(p)*vt+ dx(u)*pt+dy(v)*pt) +int 2 d(dom, qforder=5)(-(1. /dt)*convect([up, vp], -dt, up)*ut -(1. /dt)*convect([up, vp], -dt, vp)*vt) + on(1, 3, u=0, v=0)+ on(4, p=8*H/Re) + on(2, p=0) ; -5 problem streamlines(psi, psit)= int 2 d(dom, qforder=5)(dx(psi)*dx(psit)+dy(psi)*dy(psit)) +int 2 d(dom, qforder=5)(-psit*(dy(u)-dx(v))) + on(1, psi=0); real[int] yy(201), yyu(201); uth=4*y*(1 -y); u=0; v=0; p=0; for (i=0; i<=500; i++) { up=u; vp=v; NS; if (!(i % 100)) plot(psi, wait=0, bw=0, value=1, nbiso=10, ps="psi_"+i*dt+". eps"); if (!(i % 100)) { ofstream file("u_"+i*dt+". txt"); for (int jj=0; jj<=200; jj++) { x=H/2. ; y=(jj*0. 005); yy[jj]=y; yyu[jj]=u; file << yyu[jj] << " "<< yy[jj] << endl; }} };

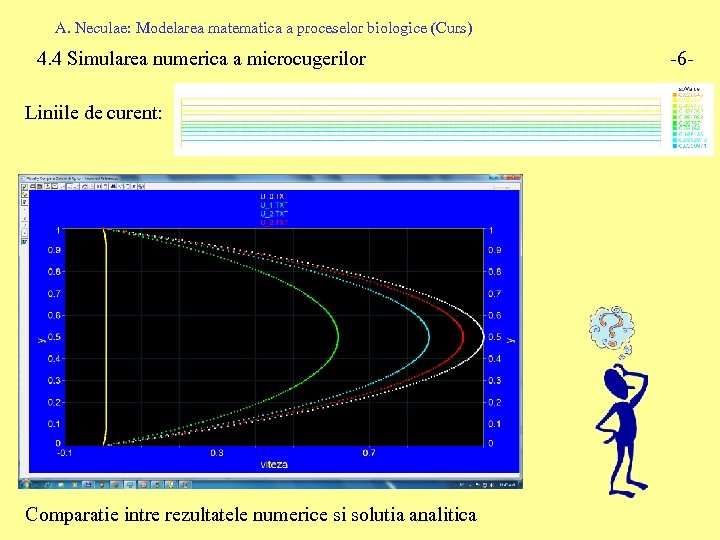
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor Liniile de curent: Comparatie intre rezultatele numerice si solutia analitica -6 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor Exercitiul 2: Curgerea Couette intre doua plane cu conditii Dirichlet in viteza pe frontierele 1 si 3, respectiv in presiune pe frontierele 2 si 4 Solutie analitica: -7 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor real A=1. ; real H=10. ; int i=0; real Re=50. ; real dt=0. 05; border a (t=0, H) {x=t; y=0; label=1; }; border b (t=0, A) {x=H; y=t; label=2; }; border c (t=H, 0) {x=t; y=A; label=3; }; border d (t=A, 0) {x=0; y=t; label=4; }; mesh dom=buildmesh(a(80) +b(20) +c(80) +d(20)); plot (dom, wait=1); fespace Vh(dom, P 2); fespace Ph(dom, P 1); Vh u, v, ut, vt, uth, up, vp, psit; Ph p, pt; problem NS(u, v, p, ut, vt, pt, solver=Crout, eps=1. e-8, init=i)= int 2 d(dom, qforder=5)((1. /dt)*(u*ut+v*vt)+ (1/Re)*(dx(u)*dx(ut)+dy(u)*dy(ut)+ dx(v)*dx(vt)+dy(v)*dy(vt))+ p*pt*(0. 00000001)+dx(p)*ut+dy(p)*vt+ dx(u)*pt+dy(v)*pt) +int 2 d(dom, qforder=5)( -(1. /dt)*convect([up, vp], -dt, up)*ut -(1. /dt)*convect([up, vp], -dt, vp)*vt) + on(1, u=0) + on(3, u=1) + on(2, 4, p=100); -8 - problem streamlines(psi, psit)= int 2 d(dom, qforder=5)(dx(psi)*dx(psit)+dy(psi)*dy(psit)) +int 2 d(dom, qforder=5)(-psit*(dy(u)-dx(v))) + on(1, psi=0) + on(3, psi=y); real[int] yy(201), yyu(201); uth=y; u=0; v=0; for (i=0; i<=500; i++) { up=u; vp=v; NS; streamlines; if (!(i % 100)) plot(psi, wait=0, bw=0, value=1, nbiso=10, ps="psi_"+i*dt+". eps"); if (!(i % 100)) { ofstream file("u_"+i*dt+". txt"); for (int jj=0; jj<=200; jj++) { x=H/2. ; y=(jj*0. 005); yy[jj]=y; yyu[jj]=u; file << yyu[jj] << " "<< yy[jj] << endl; } } };

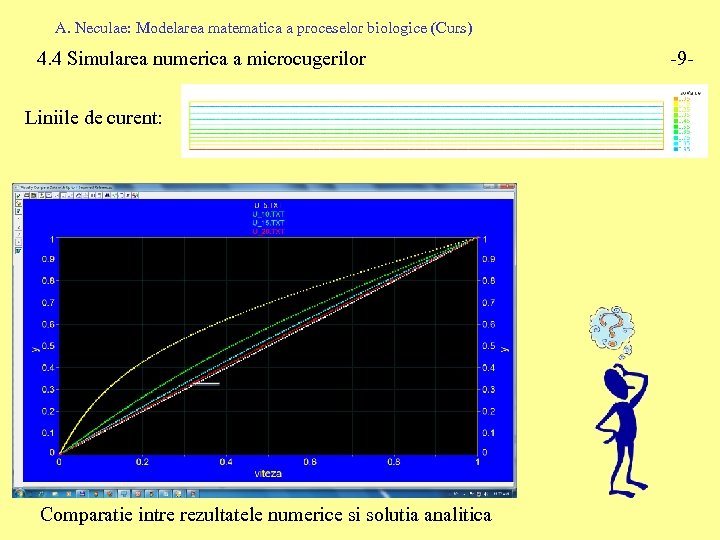
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor Liniile de curent: Comparatie intre rezultatele numerice si solutia analitica -9 -

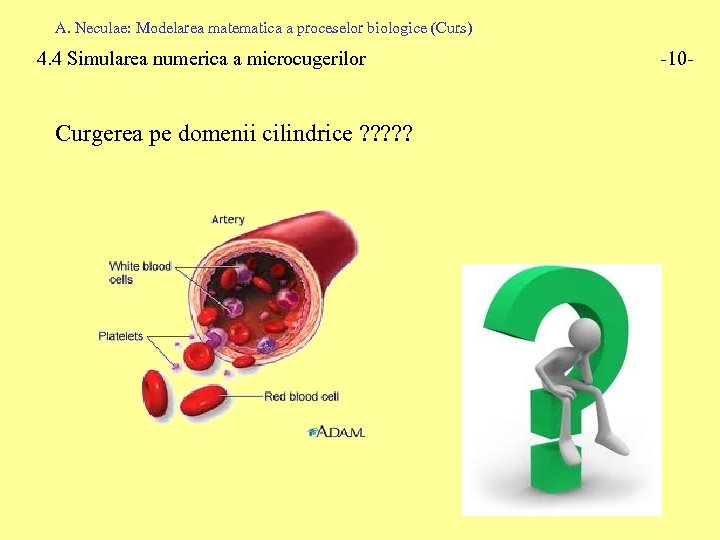
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor Curgerea pe domenii cilindrice ? ? ? -10 -

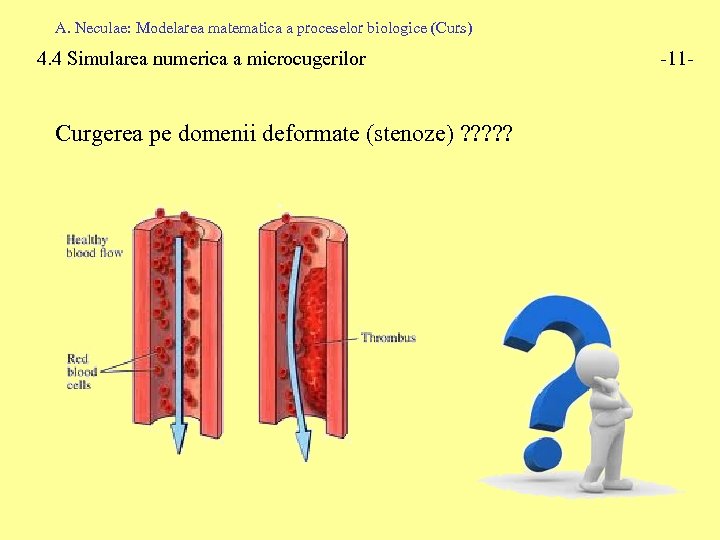
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor Curgerea pe domenii deformate (stenoze) ? ? ? -11 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 4. 4 Simularea numerica a microcugerilor Curgerea pe domenii cilindrice bifurcate ? ? ? -12 -