af721d056c0b2774b5a1171a636e8c24.ppt
- Количество слайдов: 48

Modelarea matematica a proceselor biologice - Curs -

Structura cursului: Cap. 1: Introducere in modelarea numerica a proceselor biologice Cap. 2: Ecuatii de transport Cap. 3: Difuzia. Conductia termica. Cap. 4: Microcurgeri

Cap. 5: Micropicaturi Cap. 6: Transportul speciilor biochimice Cap. 7: Reactii biochimice Cap. 8: Curgerea si transportul de masa in domenii variabile Cap. 9: Transportul in camp magnetic Cap. 10: Transportul in camp electric

BIBLIOGRAFIE: 1) Friedman M. H. 2008, Principles and models of biological transport; Springer. 2) Kojic M, et al. 2008, Computer modeling in bioengineering; Wiley & Sons. 3) Berthier J. , Silberzan P. 2005, Microfluidics for Biotechnology; Artech House, Boston/London. 4) Alberts B, et al. 2002 Molecular biology of the cell; 4 th ed. New York, Garland Science. 5) Perthame B. 2007 Transport equations in biology; Birkhauser Verlag. 6) Dym C. 2004 Principles of mathematical modelling; Academic Press.

A. Neculae: Modelarea matematica a proceselor biologice (Curs) Capitolul 3: Difuzia. Conductia termica 3. 1 Miscarea Browniana 3. 2 Ecuatia macroscopica a difuziei 3. 3 Forma adimensionalizata a ecuatiei difuziei 3. 4 Difuzia si sedimentarea 3. 5 Abordarea microscopica. Metoda Monte Carlo 3. 6 Conductia termica 3. 7 Simularea numerica a proceselor de difuzie si conductie (seminar)

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 1 Miscarea Browniana - Miscare la scara microscopica descoperita de biologii J. Ingenhousz (1730 -1799) si R. Brown (1773 -1858) - Agitatia moleculelor depinde de temperatura - Drum liber mediu = distanta parcursa intre doua ciocniri consecutive Parcursul unei nanoparticule intr-un fluid la doua momente de timp [3]:

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 1 Miscarea Browniana -2 - Miscarea Browniana

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 1 Miscarea Browniana -3 - Difuzia -1

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 1 Miscarea Browniana -4 - Difuzia -2
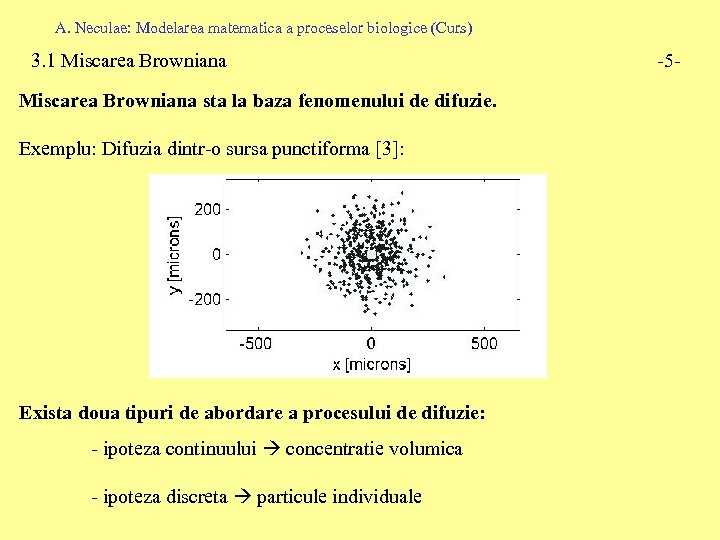
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 1 Miscarea Browniana sta la baza fenomenului de difuzie. Exemplu: Difuzia dintr-o sursa punctiforma [3]: Exista doua tipuri de abordare a procesului de difuzie: - ipoteza continuului concentratie volumica - ipoteza discreta particule individuale -5 -
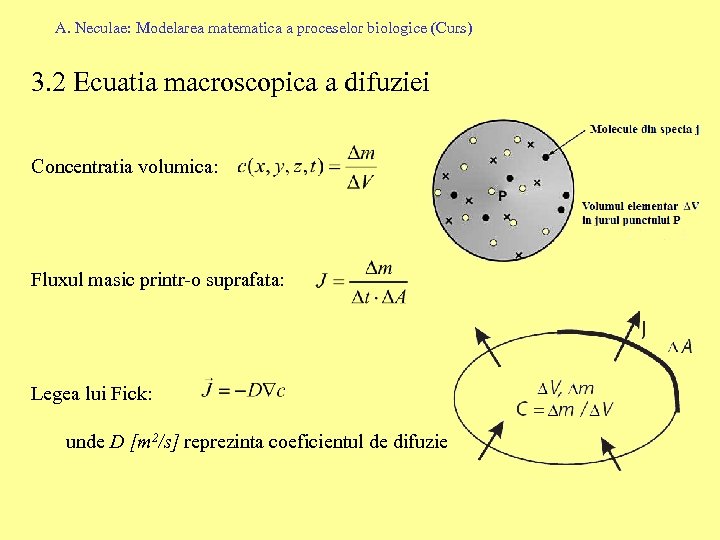
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 2 Ecuatia macroscopica a difuziei Concentratia volumica: Fluxul masic printr-o suprafata: Legea lui Fick: unde D [m 2/s] reprezinta coeficientul de difuzie

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 2 Ecuatia macroscopica a difuziei -2 - Forma diferentiala a ecuatiei difuziei: unde S este termenul sursa - daca D este constant: In medii anizotrope: - tensorul de difuzie - Legea lui Fick:
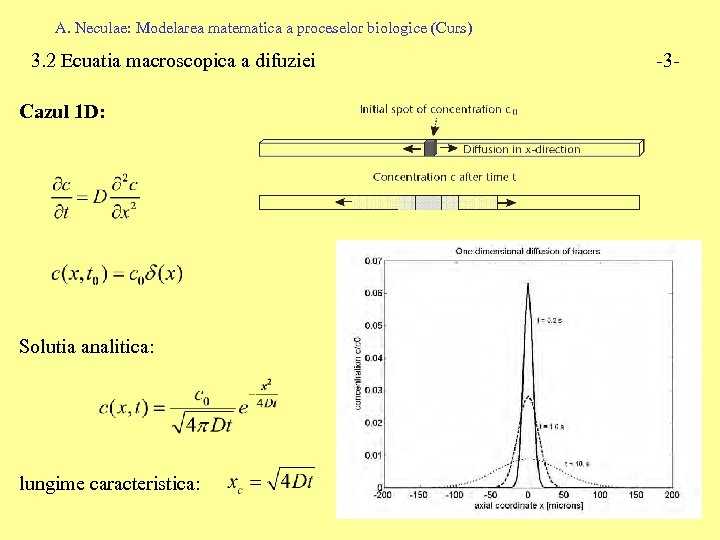
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 2 Ecuatia macroscopica a difuziei Cazul 1 D: Solutia analitica: lungime caracteristica: -3 -
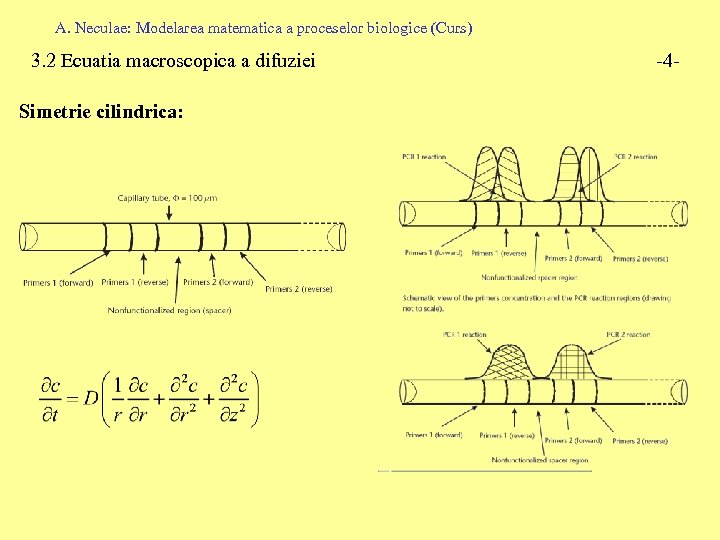
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 2 Ecuatia macroscopica a difuziei Simetrie cilindrica: -4 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 2 Ecuatia macroscopica a difuziei Simetrie sferica: - Cazul nestationar: - Cazul stationar: -5 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 3 Forma adimensionalizata a ecuatiei difuziei Cazul 1 D: Ecuatia dimensionala: Adimensionalizare: Ecuatia adimensionalizata:

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 3 Forma adimensionalizata a ecuatiei difuziei Cazul simetriei cilindrice: Ecuatia dimensionala: Adimensionalizare: Ecuatia adimensionalizata: -2 -
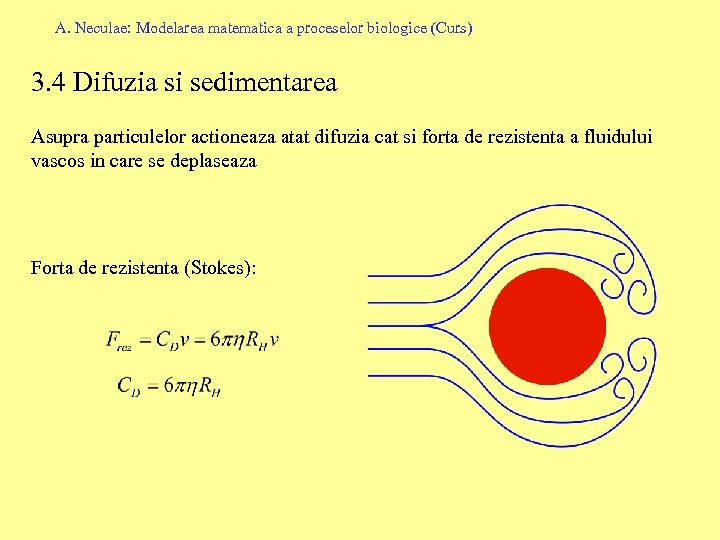
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 4 Difuzia si sedimentarea Asupra particulelor actioneaza atat difuzia cat si forta de rezistenta a fluidului vascos in care se deplaseaza Forta de rezistenta (Stokes):

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 4 Difuzia si sedimentarea -2 - La echilibru: Pentru particule sferice: Timpi caracteristici pentru sedimentare, respectiv miscarea Browniana: Daca In general, particulele cu , predomina sedimentarea. sunt afectate de sedimentare

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 5 Abordarea microscopica. Metoda Monte Carlo Cazul 2 D Domeniu 2 D cu sursa punctiforma [3]:
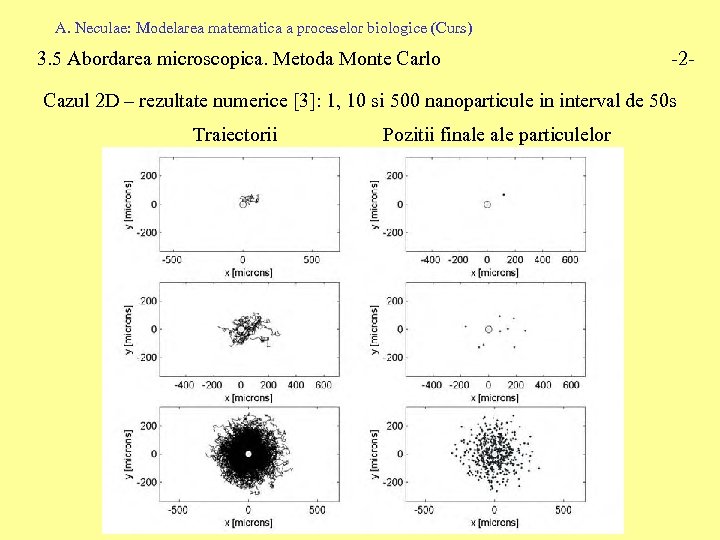
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 5 Abordarea microscopica. Metoda Monte Carlo -2 - Cazul 2 D – rezultate numerice [3]: 1, 10 si 500 nanoparticule in interval de 50 s Traiectorii Pozitii finale particulelor
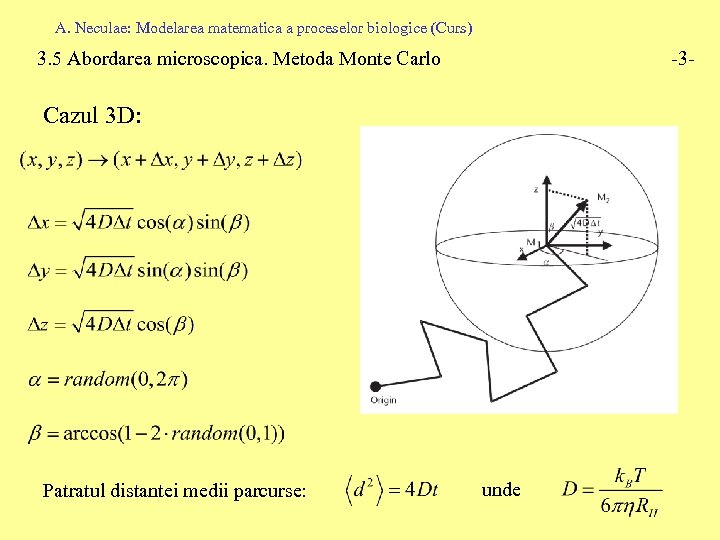
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 5 Abordarea microscopica. Metoda Monte Carlo -3 - Cazul 3 D: Patratul distantei medii parcurse: unde

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 6 Conductia termica Legea lui Fourier: unde k reprezinta coeficientul de conductivitate termica Forma diferentiala a ecuatiei conductiei: unde ST este termenul sursa - daca k este constant: In medii anizotrope: - tensorul conductivitatii termice

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 6 Conductia termica Adimensionalizare (Cazul 1 D) : Ecuatia dimensionala: Adimensionalizare: Ecuatia adimensionalizata: -2 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie (seminar) Exemplul 1: Difuzia stationara Ecuatia dimensionala: Adimensionalizare: Ecuatia adimensionalizata:

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie Fara termen sursa (s=0) si cu conditii Dirichlet pe frontierele 2 si 4 Formulare variationala (formula Green) -2 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie border a (t=0, 10) {x=t; y=0; label=1; }; border b (t=0, 1) {x=10; y=t; label=2; }; border cc (t=10, 0) {x=t; y=1; label=3; }; border d (t=1, 0) {x=0; y=t; label=4; }; plot(a(100)+b(10)+cc(100)+d(10), wait=1); mesh dom=buildmesh(a(100)+b(10)+cc(100)+d(10)); plot (dom, wait=1); fespace Vh(dom, P 2); Vh c, ct, cref; cref=1 -0. 1*x; problem difuzie(c, ct)= int 2 d(dom)(dx(c)*dx(ct)+dy(c)*dy(ct)) + on(4, c=1) + on(2, c=0); difuzie; plot(c, wait=0, value=1, nbiso=10, ps="concentratie. eps"); -3 - real[int] tabx(101), tabc(101); { ofstream file("C. txt"); for (int jj=0; jj<=100; jj++) { x=(jj*0. 1); y=0. 5; tabx[jj]=x; tabc[jj]=c; file << tabx[jj] << " "<< tabc[jj] << endl; } } { ofstream file("Cref. txt"); for (int jj=0; jj<=100; jj++) { x=(jj*0. 1); y=0. 5; tabx[jj]=x; tabc[jj]=cref; file << tabx[jj] << " "<< tabc[jj] << endl; } }

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -4 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -5 - Exemplul 2: Difuzia stationara intr-un domeniu cu simetrie circulara cu considerarea termenului sursa si implementarea unor conditii pe frontiera mixte (Dirichlet pe 1 si Neumann pe 2) unde am ales

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -6 - real R=1; func s=x^2+y^2; func g=exp(-x^2 -y^2); border a (t=0, 2*pi) {x=R*cos(t); y=R*sin(t); label=1; }; border b (t=0, 2*pi) {x=0. 25*R*cos(t); y=0. 25*R*sin(t); label=2; }; plot(a(50)+b(-20), wait=1); mesh dom=buildmesh(a(60)+b(-30)); real[int] tabx(101), tabc(101); plot (dom, wait=1); { fespace Vh(dom, P 2); ofstream file("C. txt"); Vh c, ct; for (int jj=0; jj<=100; jj++) problem difuziecircular(c, ct)= { int 2 d(dom)(dx(c)*dx(ct)+dy(c)*dy(ct)) x=0. 25+jj*0. 0075; +int 2 d(dom)(-s*ct) y=0. ; +int 1 d(dom, 1)(-g*ct) tabx[jj]=x; + on(2, c=1); tabc[jj]=c; difuziecircular; plot(c, wait=0, value=1, nbiso=10, ps="concentratie. eps"); file << tabx[jj] << " "<< tabc[jj] << endl; } }

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -7 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie Exemplul 3: Difuzia nestationara pe domeniu dreptunghiular (S=0) Ecuatia dimensionala: Adimensionalizare: Ecuatia adimensionalizata: -8 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie Evaluarea derivatei temporale: Evaluarea valorii la pasul m+1 in functie de valoarea de la pasul m: Conditia initiala: -9 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie Conditii Dirichlet pe frontierele 2 si 4; Flux nul pe frontierele 1 si 3; Conditie initiala: C 0=0 la t 0=0. -10 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) for(int i=0; i<100; i++) { { ofstream file("variatie_concentratie. txt", append); x=1; y=0. 5; tabx[jj]=x; taby[jj]=y; tabc[jj]=c; file << i*dt << " " << tabx[jj] << " " << taby[jj] << " " << tabc[jj] << endl; } difuzie; plot(c, wait=0, value=1, nbiso=20); cold=c; if (!(i % 10)) { { ofstream file("C_"+i*dt+". txt"); for (int jj=0; jj<=100; jj++) { x=(jj*0. 1); y=0. 5; tabx[jj]=x; tabc[jj]=c; file << tabx[jj] << " "<< tabc[jj] << endl; } } plot(c, wait=0, value=1, nbiso=20, ps="concentratie_"+i*dt+". eps"); } }; { ofstream file("Cref. txt"); for (int jj=0; jj<=100; jj++) { x=(jj*0. 1); y=0. 5; tabx[jj]=x; tabc[jj]=cref; file << tabx[jj] << " "<< tabc[jj] << endl; } } -11 - border a (t=0, 10) {x=t; y=0; label=1; }; border b (t=0, 1) {x=10; y=t; label=2; }; border cc (t=10, 0) {x=t; y=1; label=3; }; border d (t=1, 0) {x=0; y=t; label=4; }; plot(a(100)+b(10)+cc(100)+d(10), wait=1); mesh dom=buildmesh(a(100)+b(10)+cc(100)+d(10)); plot (dom, wait=1); fespace Vh(dom, P 2); Vh c, ct, cref, cold; //solutia analitica cref=1 -0. 1*x; int i=0; int jj=0; real dt=0. 5; real D=1; problem difuzie(c, ct)= int 2 d(dom)(1/dt*c*ct) +int 2 d(dom)(D*(dx(c)*dx(ct)+dy(c)*dy(ct))) -int 2 d(dom)(1/dt*cold*ct) + on(4, c=1) + on(2, c=0); //conditia initiala cold=0; real[int] tabx(101), taby(101), tabc(101);

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -12 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie Exemplul 4: Difuzia nestationara pe domeniu cilindric In cazul simetriei axiale : Ecuatia dimensionala: Adimensionalizare: Ecuatia adimensionalizata: -13 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -14 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -15 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie border a (t=0, 10) {x=t; y=0; label=1; }; border b (t=0, 1) {x=10; y=t; label=2; }; border cc (t=10, 0) {x=t; y=1; label=3; }; border d (t=1, 0) {x=0; y=t; label=4; }; plot(a(100)+b(10)+cc(100)+d(10), wait=1); mesh dom=buildmesh(a(100)+b(10)+cc(100)+d(10)); plot (dom, wait=1); fespace Vh(dom, P 2); Vh c, ct, cref, cold; int i=0; int jj=0; real dt=0. 5; real D=1; problem difuzie(c, ct)= int 2 d(dom)(1/dt*c*ct) +int 2 d(dom)(D*(dx(c)*dx(ct)+dy(c)*dy(ct)-1/y*dy(c)*ct)) -int 2 d(dom)(1/dt*cold*ct) + on(4, c=1) + on(2, c=0); //conditia initiala cold=0; real[int] tabx(101), taby(101), tabc(101); -16 - for(int i=0; i<100; i++) { { ofstream file("variatie_concentratie. txt", append); x=1; y=0. 5; tabx[jj]=x; taby[jj]=y; tabc[jj]=c; file << i*dt << " " << tabx[jj] << " " << taby[jj] << " " << tabc[jj] << endl; } difuzie; plot(c, wait=0, value=1, nbiso=20); cold=c; if (!(i % 10)) { { ofstream file("C_"+i*dt+". txt"); for (int jj=0; jj<=100; jj++) { x=(jj*0. 1); y=0. 5; tabx[jj]=x; tabc[jj]=c; file << tabx[jj] << " "<< tabc[jj] << endl; } } plot(c, wait=0, value=1, nbiso=20, ps="concentratie_"+i*dt+". eps"); } };

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -17 -
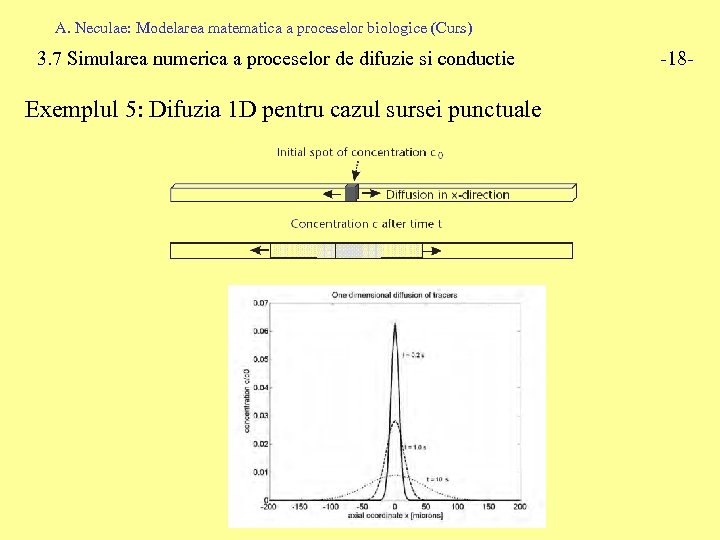
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie Exemplul 5: Difuzia 1 D pentru cazul sursei punctuale -18 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) border a (t=0, 10) {x=t; y=0; label=1; }; border b (t=0, 0. 5) {x=10; y=t; label=2; }; border cc (t=10, 0) {x=t; y=0. 5; label=3; }; border d (t=0. 5, 0) {x=0; y=t; label=4; }; plot(a(100)+b(10)+cc(100)+d(10), wait=1); mesh dom=buildmesh(a(100)+b(10)+cc(100)+d(10)); plot (dom, wait=1); fespace Vh(dom, P 2); Vh c, ct, cold; int i=0; int jj=0; real dt=0. 01; real D=1. ; //conditia initiala cold=200. *(0<x<=0. 5)+0. *(x>0. 5); plot(cold, wait=1, value=1, nbiso=20); problem difuzie(c, ct)= int 2 d(dom)(1/dt*c*ct) +int 2 d(dom)(D*(dx(c)*dx(ct)+dy(c)*dy(ct))) -int 2 d(dom)(1/dt*cold*ct); real[int] tabx(101), taby(101), tabc(101); { ofstream file("Cini. txt"); for (int jj=0; jj<=100; jj++) { x=(jj*0. 1); y=0. 5; tabx[jj]=x; tabc[jj]=cold; file << tabx[jj] << " "<< tabc[jj] << endl; } } -19 - for(int i=0; i<200; i++) { { ofstream file("variatie_concentratie. txt", append); x=1; y=0. 5; tabx[jj]=x; taby[jj]=y; tabc[jj]=c; file << i*dt << " " << tabx[jj] << " " << taby[jj] << " " << tabc[jj] << endl; } difuzie; plot(c, wait=0, value=1, nbiso=20); cold=c; if (!(i % 10)) { { ofstream file("C_"+i*dt+". txt"); for (int jj=0; jj<=100; jj++) { x=(jj*0. 1); y=0. 5; tabx[jj]=x; tabc[jj]=c; file << tabx[jj] << " "<< tabc[jj] << endl; } } plot(c, wait=0, value=1, nbiso=20, ps="concentratie_"+i*dt+". eps"); } };
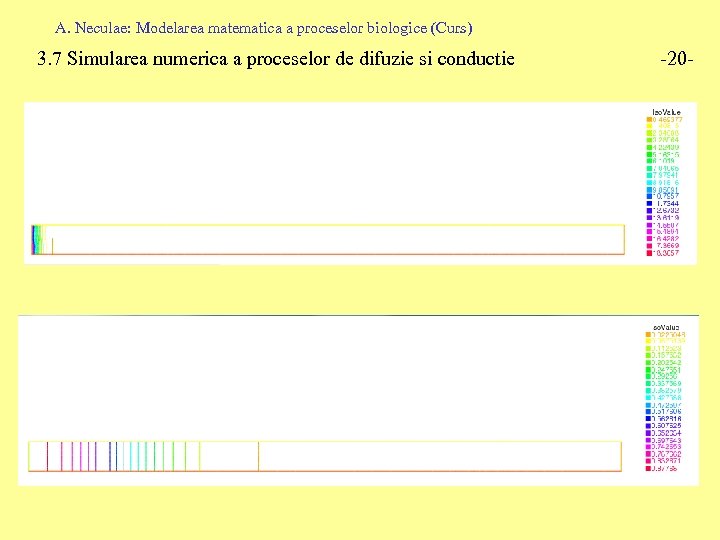
A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -20 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -21 - Exemplul 6: Conductia termica. Problema Newton Implementarea unei conditii de tip Robin: unde pe frontiera exterioara a cilindrului.

A. Neculae: Modelarea matematica a proceselor biologice (Curs) border a (t=0, 5) {x=t; y=0; label=1; }; border b (t=0, 1) {x=5; y=t; label=2; }; border c (t=5, 0) {x=t; y=1; label=3; }; border d (t=1, 0) {x=0; y=t; label=4; }; plot (a(20)+b(5)+c(20)+d(5), wait=1); mesh Dom =buildmesh(a(20)+b(5)+c(20)+d(5)); plot (Dom, wait=1); int i=0; real dt=0. 01 ; real k=1; real h=1. ; fespace Xh(Dom, P 2); Xh Told, T, Tt; Told=0; func Text=1 -0. 2*x; solve Prob 4(T, Tt)=int 2 d(Dom)(1/dt*T*Tt) +int 2 d(Dom)(k*(dx(T)*dx(Tt)+dy(T)*dy(Tt)-1/y*dy(T)*Tt)) -int 2 d(Dom)(1/dt*Told*Tt)+ int 1 d(Dom, 3)(h*T*Tt)-int 1 d(Dom, 3)(h*Text*Tt) +on(2, T=0) +on(4, T=1); for(int i=0; i<100; i++) {Prob 4; if (!(i%10)) plot(T, wait=0, value=1, nbiso=10); Told=T; }; -22 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie -23 -

A. Neculae: Modelarea matematica a proceselor biologice (Curs) 3. 7 Simularea numerica a proceselor de difuzie si conductie Difuzia in medii cu simetrie sferica ? ? ? -24 -
af721d056c0b2774b5a1171a636e8c24.ppt