Modelado Matemático de Sistemas Físicos El Algoritmo de

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides para Eliminar Singularidades Estructurales • Esta presentación trata con un algoritmo que puede usarse para la eliminación de singularidades estructurales de un modelo en forma sistemática y algorítmica. Se llama el algoritmo de Pantelides. • El algoritmo de Pantelides es un algoritmo simbólico de la reducción del índice de perturbación. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Contenido • Singularidades estructurales y el dígrafo de la estructura • El algoritmo de Pantelides Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

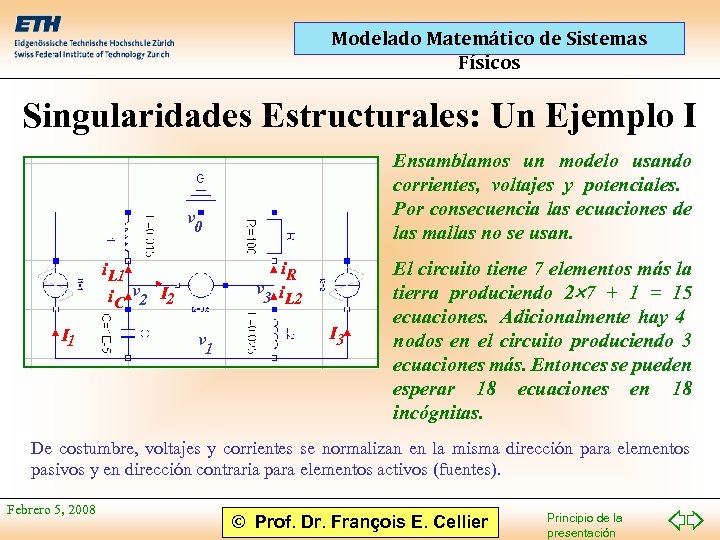Modelado Matemático de Sistemas Físicos Singularidades Estructurales: Un Ejemplo I Ensamblamos un modelo usando corrientes, voltajes y potenciales. Por consecuencia las ecuaciones de las mallas no se usan. v 0 i. R v 3 i L 2 i. L 1 i. C v 2 I 1 v 1 I 3 El circuito tiene 7 elementos más la tierra produciendo 2 7 + 1 = 15 ecuaciones. Adicionalmente hay 4 nodos en el circuito produciendo 3 ecuaciones más. Entonces se pueden esperar 18 ecuaciones en 18 incógnitas. De costumbre, voltajes y corrientes se normalizan en la misma dirección para elementos pasivos y en dirección contraria para elementos activos (fuentes). Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 /dt i. C = C · du. C /dt v 0 = 0 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 Febrero 5, 2008 03 I 3 u. R 05 i. R 06 u. L 1 07 di. L 1 /dt 08 u. L 2 09 di. L 2 /dt 10 i. C 11 du. C /dt 12 v 0 v 1 14 v 2 15 v 3 16 u 1 17 I 2 13 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 02 u 2 18 1: 2: 3: 4: 5: 6: 7: 8: I 1 04 Singularidades Estructurales: Un Ejemplo II 01 u 3 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos 01 02 03 I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 /dt i. C = C · du. C /dt v 0 = 0 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 Febrero 5, 2008 I 3 u. R i. R 06 u. L 1 07 di. L 1 /dt 08 u. L 2 09 di. L 2 /dt 10 i. C 11 du. C /dt 12 v 0 v 1 14 v 2 15 v 3 16 u 1 17 03 05 04 I 2 13 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 02 u 2 18 1: 2: 3: 4: 5: 6: 7: 8: I 1 04 Singularidades Estructurales: Un Ejemplo III 01 u 3 © Prof. Dr. François E. Cellier Principio de la presentación 13 14 15 16 17 18

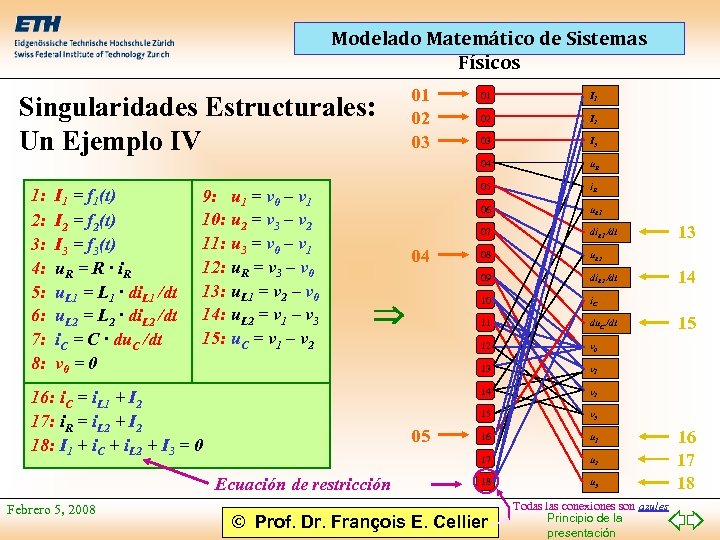Modelado Matemático de Sistemas Físicos 01 02 03 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 /dt i. C = C · du. C /dt v 0 = 0 Febrero 5, 2008 i. R u. L 1 di. L 1 /dt 08 u. L 2 di. L 2 /dt 10 i. C 11 du. C /dt 12 v 0 v 1 14 v 2 15 v 3 16 u 1 17 Ecuación de restricción u. R 09 05 I 3 07 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 03 06 I 2 05 04 02 13 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 I 1 04 Singularidades Estructurales: Un Ejemplo IV 01 u 2 18 u 3 © Prof. Dr. François E. Cellier Todas las conexiones son azules Principio de la presentación 13 14 15 16 17 18

Modelado Matemático de Sistemas Físicos Coloración del Dígrafo de la Estructura • El algoritmo de la coloración del dígrafo de la estructura es análogo al método de la coloración de las ecuaciones usado antes. • Una implementación del algoritmo usando un compilador probablemente usará el dígrafo ya que ese algoritmo puede transformarse fácilmente a estructuras de datos comunes en idiomas de la programación. • Para el ojo humano la coloración de las ecuaciones puede resultar más bien legible. Por eso continuaremos coloreando las ecuaciones en lugar del dígrafo. • La ordenación vertical puede efectuarse simultáneamente usando la renumeración de las ecuaciones. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides I • Una vez que una ecuación de restricción se encontró, esa ecuación tiene que derivarse. • Usando el algoritmo de Pantelides, la ecuación de restricción derivada se añade al sistema de ecuaciones. • Por consecuencia, el sistema de ecuaciones ahora tiene más ecuaciones que incógnitas. • El número de ecuaciones e incógnitas puede equilibrarse de nuevo eliminando uno de los integradores asociados con la ecuación de restricción. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

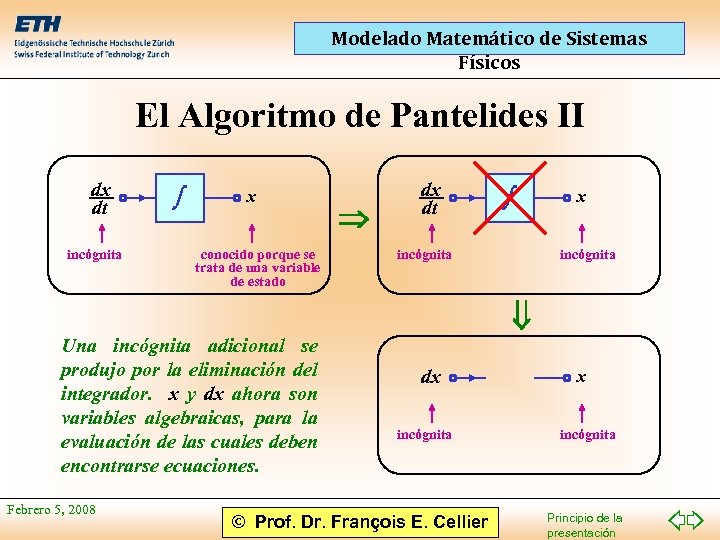Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides II dx dt incógnita x conocido porque se trata de una variable de estado dx dt incógnita x incógnita Una incógnita adicional se produjo por la eliminación del integrador. x y dx ahora son variables algebraicas, para la evaluación de las cuales deben encontrarse ecuaciones. Febrero 5, 2008 dx incógnita © Prof. Dr. François E. Cellier x incógnita Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides III • En la diferenciación de las ecuaciones de restricción puede ocurrir que variables adicionales se generan, por ejemplo v dv, donde v as una variable algebraica. • Se sabe que v ya está coloreado en azul (como se trata de una ecuación de restricción que solamente contiene variables azules). Entonces existe otra ecuación en la cual se encuentra v coloreado en rojo. • Aquella ecuación también tiene que derivarse. • La diferenciación de ecuaciones adicionales continúa hasta que no se genera ninguna variable nueva más. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides: Un Ejemplo I Integrador eliminado 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 /dt i. C = C · du. C /dt v 0 = 0 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 d. I 1 + di. C + di. L 2 + d. I 3 = 0 Nuevas variables introducidas 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides: Un Ejemplo II 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 /dt i. C = C · du. C /dt v 0 = 0 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 19: d. I 1 + di. C + di. L 2 + d. I 3 = 0 Febrero 5, 2008 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 i. C = C · du. C /dt v 0 = 0 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 19: d. I 1 + di. C + di. L 2 + d. I 3 = 0 © Prof. Dr. François E. Cellier Principio de la presentación

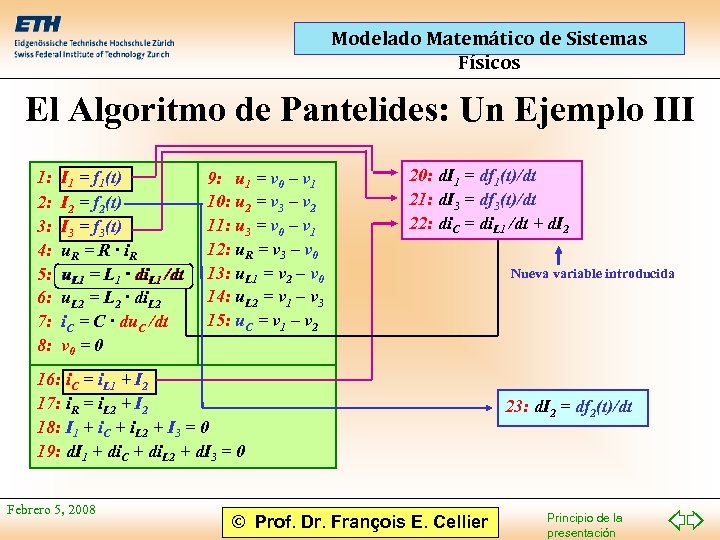Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides: Un Ejemplo III 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 i. C = C · du. C /dt v 0 = 0 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 20: d. I 1 = df 1(t)/dt 21: d. I 3 = df 3(t)/dt 22: di. C = di. L 1 /dt + d. I 2 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 19: d. I 1 + di. C + di. L 2 + d. I 3 = 0 Febrero 5, 2008 © Prof. Dr. François E. Cellier Nueva variable introducida 23: d. I 2 = df 2(t)/dt Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides: Un Ejemplo IV 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 i. C = C · du. C /dt v 0 = 0 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 19: d. I 1 + di. C + di. L 2 + d. I 3 = 0 Febrero 5, 2008 20: d. I 1 = df 1(t)/dt 21: d. I 3 = df 3(t)/dt 22: di. C = di. L 1 /dt + d. I 2 23: d. I 2 = df 2(t)/dt © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides: Un Ejemplo V 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 i. C = C · du. C /dt v 0 = 0 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 19: d. I 1 + di. C + di. L 2 + d. I 3 = 0 Febrero 5, 2008 20: d. I 1 = df 1(t)/dt 21: d. I 3 = df 3(t)/dt 22: di. C = di. L 1 /dt + d. I 2 23: d. I 2 = df 2(t)/dt © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides: Un Ejemplo VI 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 i. C = C · du. C /dt v 0 = 0 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 19: d. I 1 + di. C + di. L 2 + d. I 3 = 0 Febrero 5, 2008 20: d. I 1 = df 1(t)/dt 21: d. I 3 = df 3(t)/dt 22: di. C = di. L 1 /dt + d. I 2 23: d. I 2 = df 2(t)/dt © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides: Un Ejemplo VII 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 i. C = C · du. C /dt v 0 = 0 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 19: d. I 1 + di. C + di. L 2 + d. I 3 = 0 Febrero 5, 2008 20: d. I 1 = df 1(t)/dt 21: d. I 3 = df 3(t)/dt 22: di. C = di. L 1 /dt + d. I 2 23: d. I 2 = df 2(t)/dt © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides: Un Ejemplo VIII 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 i. C = C · du. C /dt v 0 = 0 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 19: d. I 1 + di. C + di. L 2 + d. I 3 = 0 Resulta un sistema algebraico con 7 ecuaciones en 7 incógnitas. 20: d. I 1 = df 1(t)/dt 21: d. I 3 = df 3(t)/dt 22: di. C = di. L 1 /dt + d. I 2 23: d. I 2 = df 2(t)/dt Elección Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Pantelides: Un Ejemplo IX 1: 2: 3: 4: 5: 6: 7: 8: I 1 = f 1(t) I 2 = f 2(t) I 3 = f 3(t) u. R = R · i R u. L 1 = L 1 · di. L 1 /dt u. L 2 = L 2 · di. L 2 i. C = C · du. C /dt v 0 = 0 9: u 1 = v 0 – v 1 10: u 2 = v 3 – v 2 11: u 3 = v 0 – v 1 12: u. R = v 3 – v 0 13: u. L 1 = v 2 – v 0 14: u. L 2 = v 1 – v 3 15: u. C = v 1 – v 2 16: i. C = i. L 1 + I 2 17: i. R = i. L 2 + I 2 18: I 1 + i. C + i. L 2 + I 3 = 0 19: d. I 1 + di. C + di. L 2 + d. I 3 = 0 Febrero 5, 2008 20: d. I 1 = df 1(t)/dt 21: d. I 3 = df 3(t)/dt 22: di. C = di. L 1 /dt + d. I 2 23: d. I 2 = df 2(t)/dt © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Conclusiones I • Empezamos deduciendo un sistema completo de EDAs. • El algoritmo de Tarjan de la coloración del dígrafo se aplica al sistema de EDAs. • Si se encuentra una ecuación coloreada completamente en azul, el sistema contiene una singularidad estructural. • El sistema estructuralmente singular se hace regular usando el algoritmo de Pantelides. • Puede suceder que el algoritmo de Pantelides tiene que aplicarse múltiples veces. • Cada vez el índice de perturbación se reduce por uno. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Conclusiones II • Ahora el algoritmo de Tarjan de la coloración del dígrafo se aplica al sistema de EDAs modificado (regular). • Si el algoritmo se atasca, el sistema modificado contiene al menos un bucle algebraico. La introducción de nuevos bucles algebraicos en la aplicación del algoritmo de Pantelides es muy común. • Se puede continuar con el procesamiento del sistema. El algoritmo de rasgadura es uno de los algoritmos que puede usarse para tratar con bucles algebraicos. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Referencias • Cellier, F. E. and H. Elmqvist (1993), “Automated formula manipulation supports object-oriented continuous-system modeling, ” IEEE Control Systems, 13(2), pp. 28 -38. • Pantelides, C. C. (1988), “The consistent initialization of differential-algebraic systems, ” SIAM Journal Scientific Statistical Computation, 9(2), pp. 213 -231. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación