МОДЕЛЬ ТОЧКИ общий случай ЗНАНИЯ, НЕОБХОДИМЫЕ ПРИ

Скачать презентацию МОДЕЛЬ ТОЧКИ общий случай ЗНАНИЯ, НЕОБХОДИМЫЕ ПРИ Скачать презентацию МОДЕЛЬ ТОЧКИ общий случай ЗНАНИЯ, НЕОБХОДИМЫЕ ПРИ

6_model_tochki.ppt

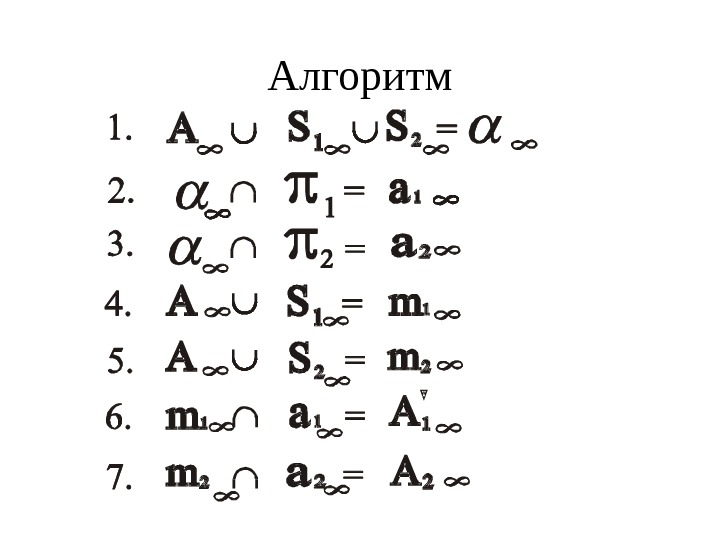
  • Размер: 2.5 Mегабайта
  • Количество слайдов: 33

Описание презентации МОДЕЛЬ ТОЧКИ общий случай ЗНАНИЯ, НЕОБХОДИМЫЕ ПРИ по слайдам

МОДЕЛЬ ТОЧКИ общий случай МОДЕЛЬ ТОЧКИ общий случай

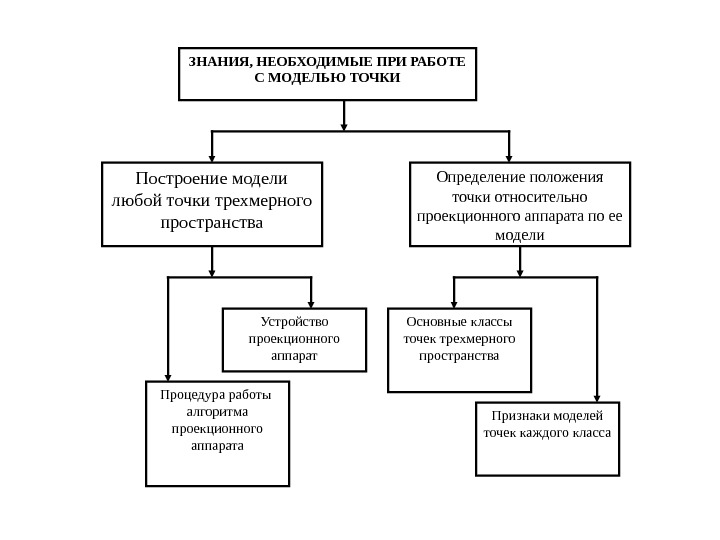
ЗНАНИЯ, НЕОБХОДИМЫЕ ПРИ РАБОТЕ С МОДЕЛЬЮ ТОЧКИ Построение модели любой точки трехмерного пространства Определение положения точкиЗНАНИЯ, НЕОБХОДИМЫЕ ПРИ РАБОТЕ С МОДЕЛЬЮ ТОЧКИ Построение модели любой точки трехмерного пространства Определение положения точки относительно проекционного аппарата по ее модели Устройство проекционного аппарат Процедура работы алгоритма проекционного аппарата Признаки моделей точек каждого класса. Основные классы точек трехмерного пространства

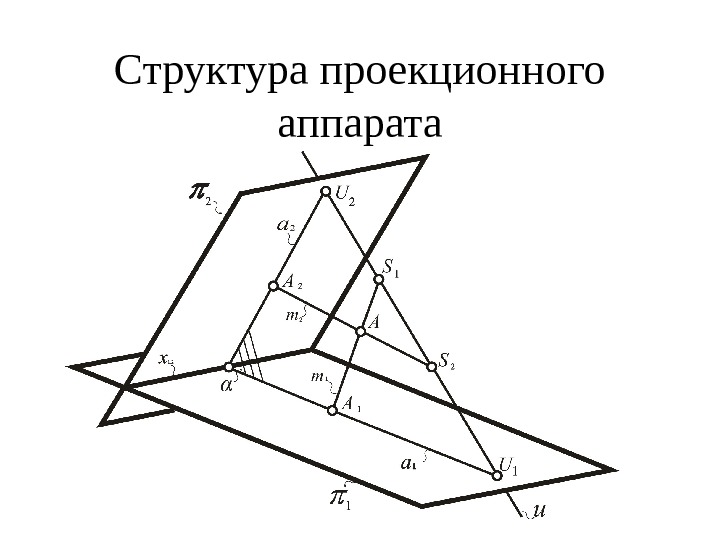
Структура проекционного аппарата Структура проекционного аппарата

Алгоритм 1) A u = – проецирующая плоскость; )2 1 = а 1 – линияАлгоритм 1) A u = – проецирующая плоскость; )2 1 = а 1 – линия связи; ) 3 2 = a 2 – линия связи; 4) А S 1 = m 1 , – проецирующая прямая; 5) А S 2 = m 2 – проецирующая прямая; 6) m 1 а 1 = A 1 – первая проекция точки A ; 7) m 2 a 2 = A 2 — вторая проекция точки A.

Модель точки трехмерного пространства, построенной методом двух изображений - два ее изображения (проекции), которые принадлежатМодель точки трехмерного пространства, построенной методом двух изображений — два ее изображения (проекции), которые принадлежат двойной линии связи, проходящей через двойную исключенную точку.

КЛАССИФИКАЦИЯ ТОЧЕК ТРЕХМЕРНОГО ПРОСТРАНСТВА • 1. Точки частного положения • Точки принадлежащие картинам. •КЛАССИФИКАЦИЯ ТОЧЕК ТРЕХМЕРНОГО ПРОСТРАНСТВА • 1. Точки частного положения • Точки принадлежащие картинам. • Бесконечно удаленные точки. • Точки, принадлежащие нейтральной плоскости. • Точки, принадлежащие плоскостям тождества. • 2. Точки общего положения

Задача 1. Построение плоской модели точки трехмерного пространства перспектива Задача 1. Построение плоской модели точки трехмерного пространства перспектива

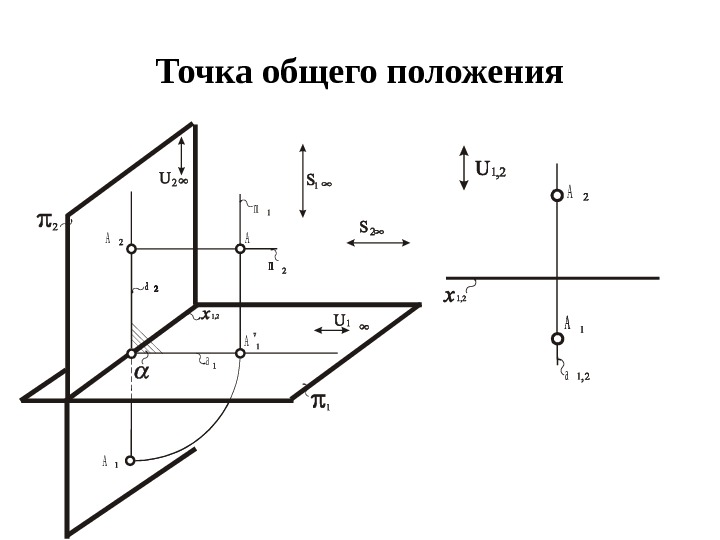
Модель точки общего положения Модель точки общего положения

Алгоритм Алгоритм

Модели точек частного положения Характерные признаки Модели точек частного положения Характерные признаки

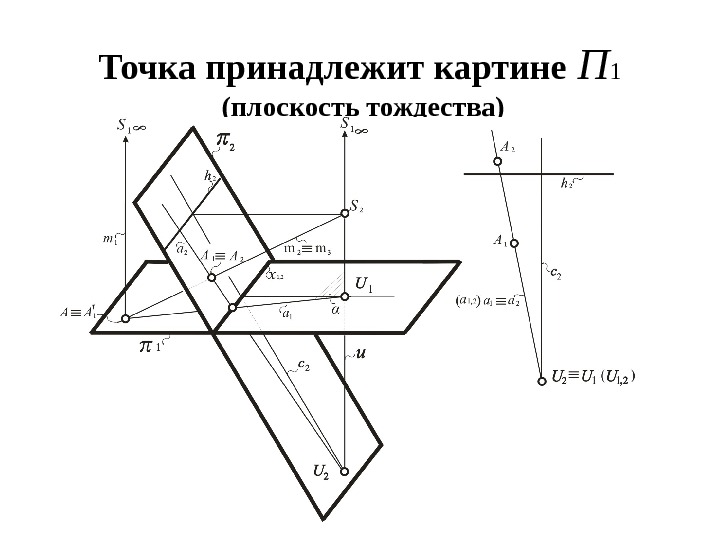
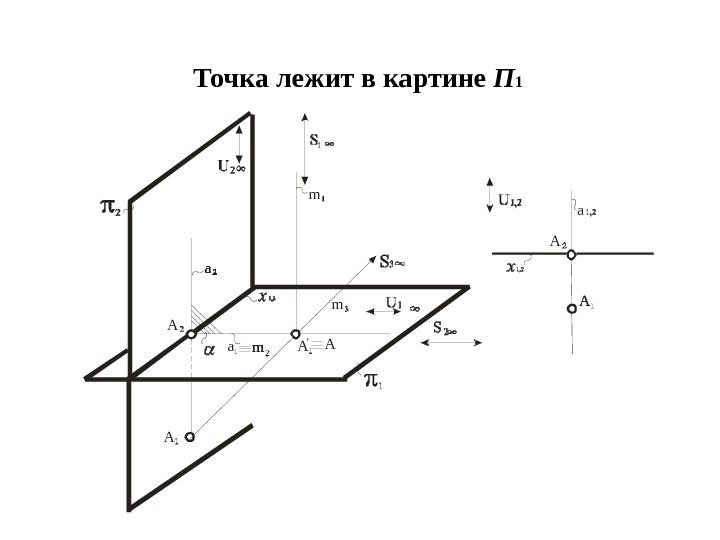
Точка принадлежит картине П 1 (плоскость тождества) Точка принадлежит картине П 1 (плоскость тождества)

Алгоритм Алгоритм

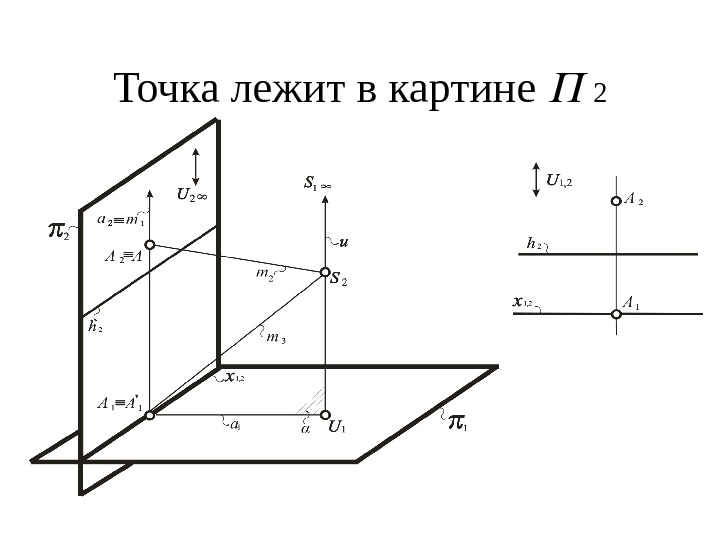
Точка лежит в картине 2 Точка лежит в картине

Алгоритм Алгоритм

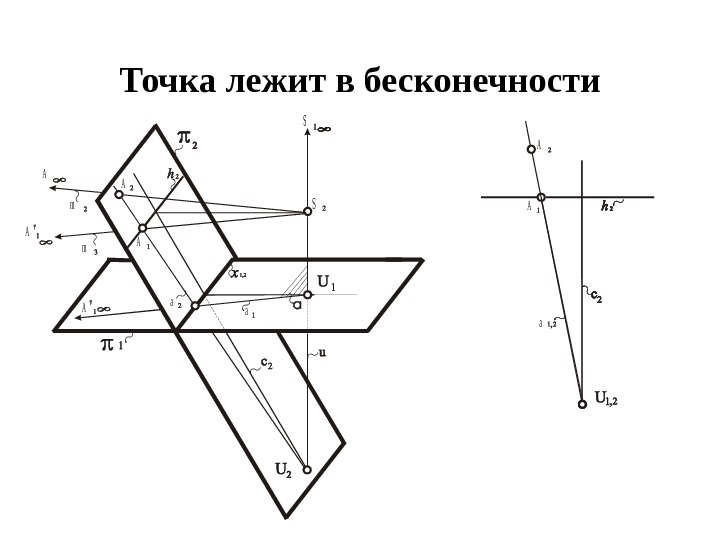
Точка лежит в бесконечности. А А а m S S А А а А Точка лежит в бесконечности. А А а m S S А А а А

Алгоритм Алгоритм

Точка лежит в нейтральной плоскости Перспектива на наклонной картинеm S SSS а m а А АТочка лежит в нейтральной плоскости Перспектива на наклонной картинеm S SSS а m а А А А а А

Алгоритм Алгоритм

Точка лежит в нейтральной плоскости Перспектива на вертикальной картине. А m АА а mmmm А аТочка лежит в нейтральной плоскости Перспектива на вертикальной картине. А m АА а mmmm А а m АА А

Алгоритм Алгоритм

Задача 1. Построение плоской модели точки трехмерного пространства Эпюр Монжа Задача 1. Построение плоской модели точки трехмерного пространства Эпюр Монжа

Точка общего положенияа mmmm А А ааа m АА а АА А Точка общего положенияа mmmm А А ааа m АА а АА А

Алгоритмα Алгоритмα

Модели точек частного положения Характерные признаки Модели точек частного положения Характерные признаки

Точка лежит в картине П 1 а АА А аmmmm А ааа m А АА mТочка лежит в картине П 1 а АА А аmmmm А ааа m А АА m

Алгоритм Алгоритм

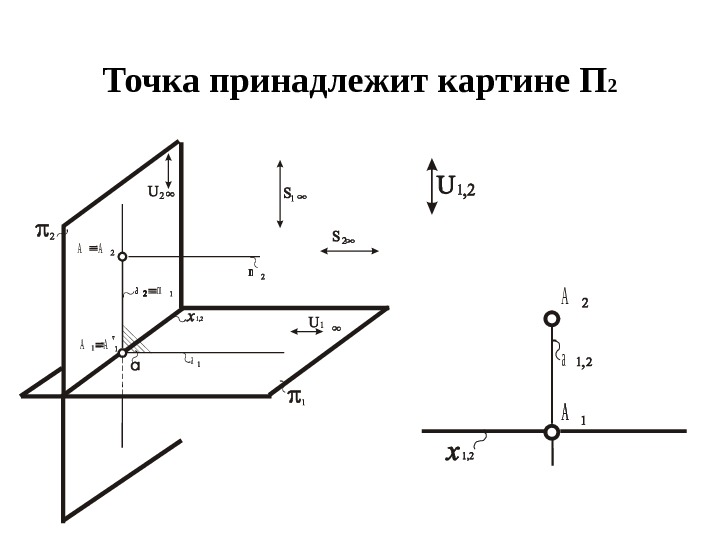
Точка принадлежит картине П 2 а mmmm АА аааm АА а АА А Точка принадлежит картине П 2 а mmmm АА аааm АА а АА А

Алгоритм Алгоритм

Точка находится в бесконечности (в нейтральной плоскости)А А АА АА А Точка находится в бесконечности (в нейтральной плоскости)А А АА АА А

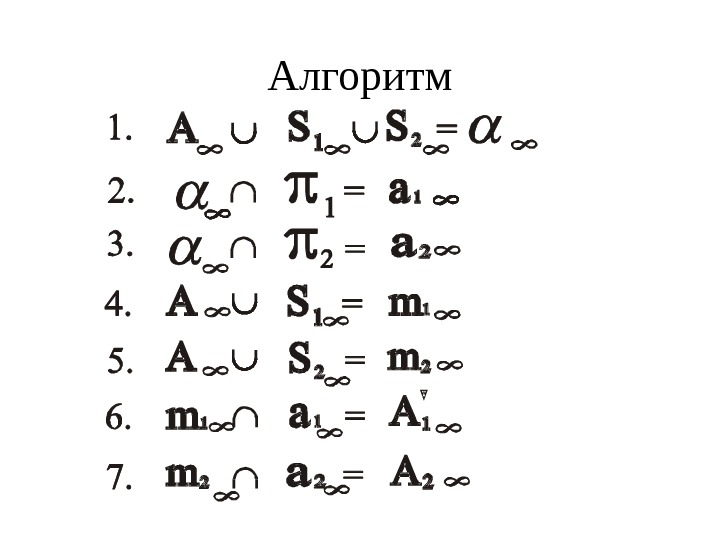Алгоритм Алгоритм

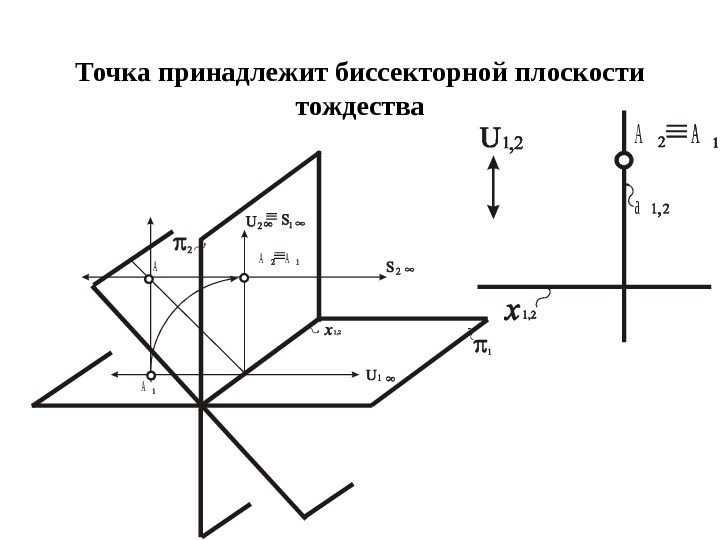
Точка принадлежит биссекторной плоскости тождестваа ААА А А АА Точка принадлежит биссекторной плоскости тождестваа ААА А А АА

Алгоритм Алгоритм

Зарегистрируйтесь, чтобы просмотреть полный документ!
РЕГИСТРАЦИЯ