Model Selection in Semiparametrics and Measurement Error Models

Model Selection in Semiparametrics and Measurement Error Models Raymond J. Carroll Department of Statistics Faculty of Nutrition and Toxicology Texas A&M University http: //stat. tamu. edu/~carroll

Outline § Problem motivating the work § Measurement error in nutritional epidemiology § Power of model selection/averaging § Difficulties with BIC § Semiparametric formulation § The Hjort and Claeskens asymptotics § Major results on semiparametric efficiency

Co-authors, Nutritional Epidemiology Victor Kipnis National Cancer Institute Laurence Freedman, Gertner Institute (Israel) and National Cancer Institute

Co-author, Semiparametrics Gerda Claeskens, University of Leuvan

Papers § Seemingly Unrelated Measurement Error Models, Biometrics, 2006, Victor Kipnis and Larry Freedman § Post-Model Selection Inference in Semiparametric Models, with Gerda Claeskens § This paper has been under review for 6 months, at a journal that just asked me to review a paper in 6 weeks.

Seemingly Unrelated Measurement Error Models (SUMEM) § Problem: Understand the properties of food frequency questionnaires (FFQ), the most used means of estimating nutrient intakes § Issue: True intake cannot be measured

SUMEM § Notation: § Y = FFQ § X = true intake (Not Observable) § Z = other covariates § Goals: Estimate two important properties § For pre-study sample sizes § post-study relative risk and power

The OPEN Study § I will use data from the OPEN Study § First large biomarker study for nutritional epidemiology § Biomarkers available: § Protein (urinary nitrogen) § Energy/Calories (Doubly labeled water) § Approximately 200 women in the study

SUMEM: Model for Protein § Basic variance components model: § Error Model for Biomarker:

SUMEM: Model for Protein § More Data: Along with Protein, we also measure Energy (calories) § Correlated: § Energy = Protein + Fat + Carbohydrates + Alcohol § Combine: We try to combine energy with protein

SUMEM: Model for Protein § Variance components model with Energy: Note how this model predicts FFQ protein using true energy § Error Model for Biomarker:

SUMEM: More pain, no gain § Variance components model with Energy: Note how this model predicts FFQ protein using true energy § No Gain: One can show that if you fit this measurement error model, § Marginal protein fit unaffected, identical estimates of correlation and attenuation

SUMEM: More pain, no gain § Variance components model with Energy: Note how this model predicts FFQ protein using true energy § Intuition: To predict FFQ Protein: § If I tell you true protein intake, why should true energy intake matter?

SUMEM: More pain, more gain? § Variance components model with Energy: Full Model § A reduced model: Reduced Model

OPEN Biomarker Study Results § Variance Reduction: As if the sample size increased by a factor of 3 (s. e. from Burnham & Anderson) Model Correlation Full Reduced Estimate 0. 282 0. 250 Std. err. 0. 088 0. 048 Attenuation Full Reduced 0. 129 0. 114 0. 041 0. 024

OPEN: Model Selection § AIC and Weights: Let be the likelihood ratio chi-squared statistic, full vs. reduced § Let d be the difference in degrees of freedom § The AIC weight to the reduced model is § We can do a weighted average of the full and reduced model estimates

OPEN: Model Selection § BIC and Weights: Let be the likelihood ratio chi-squared statistic, full vs. reduced § Let d be the difference in degrees of freedom § The BIC weight to the reduced model is

OPEN: Model Selection § In OPEN: the AIC weight to the reduced model is § We can do a weighted average of the full and reduced model estimates § In OPEN, this is obviously essentially the reduced model

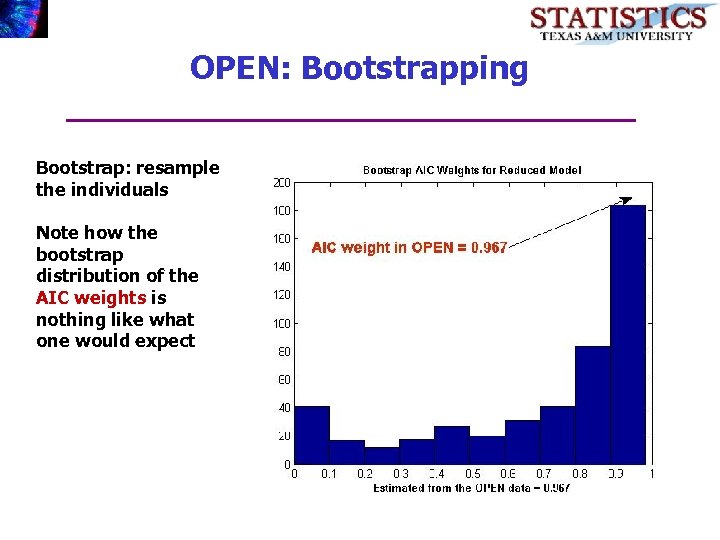OPEN: Bootstrapping Bootstrap: resample the individuals Note how the bootstrap distribution of the AIC weights is nothing like what one would expect

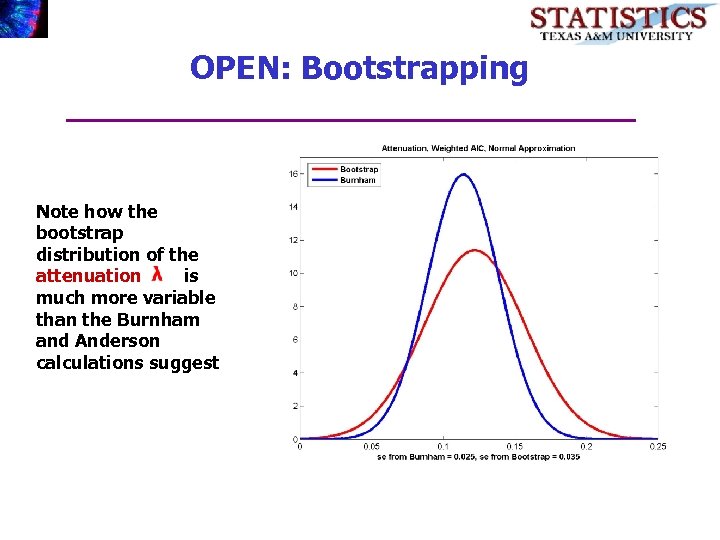OPEN: Bootstrapping Note how the bootstrap distribution of the attenuation is much more variable than the Burnham and Anderson calculations suggest

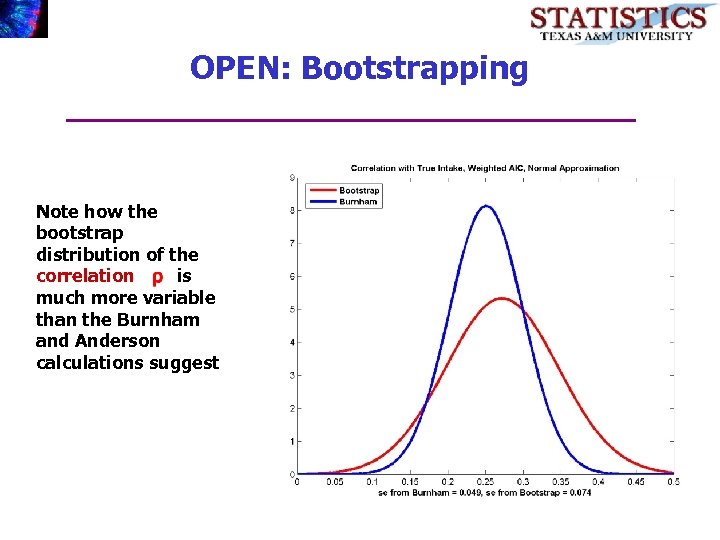OPEN: Bootstrapping Note how the bootstrap distribution of the correlation is much more variable than the Burnham and Anderson calculations suggest

OPEN Type Simulation § Setup: We used OPEN parameters, but put in a full model § n = 200, as in OPEN § BIC is supposed to be a consistent model selector, hence should have weights near 0. § AIC is not a consistent model selector

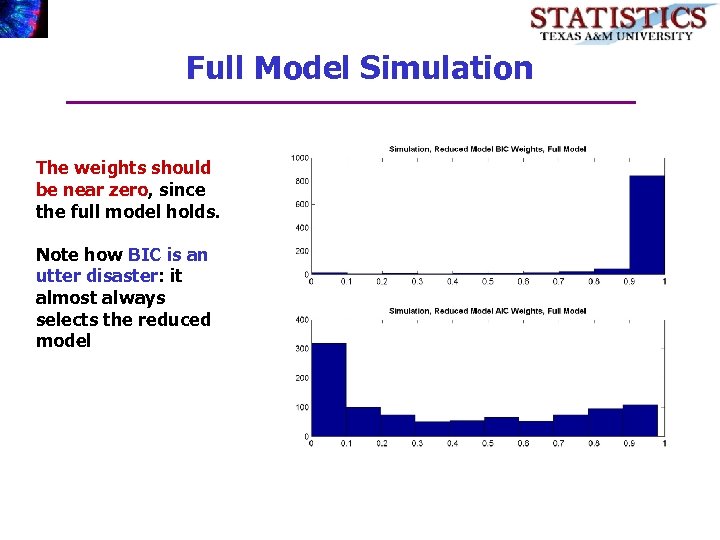Full Model Simulation The weights should be near zero, since the full model holds. Note how BIC is an utter disaster: it almost always selects the reduced model

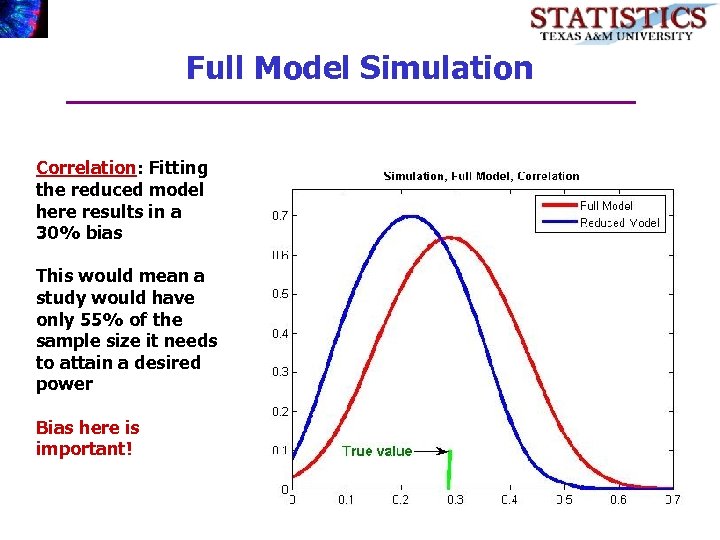Full Model Simulation Correlation: Fitting the reduced model here results in a 30% bias This would mean a study would have only 55% of the sample size it needs to attain a desired power Bias here is important!

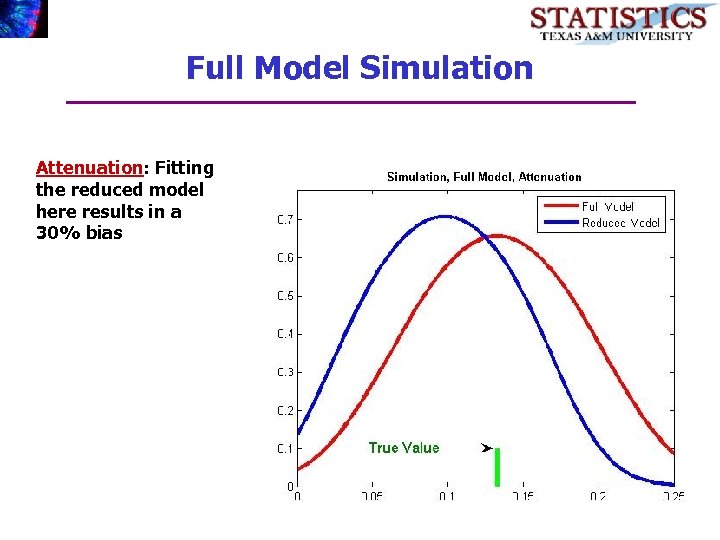Full Model Simulation Attenuation: Fitting the reduced model here results in a 30% bias

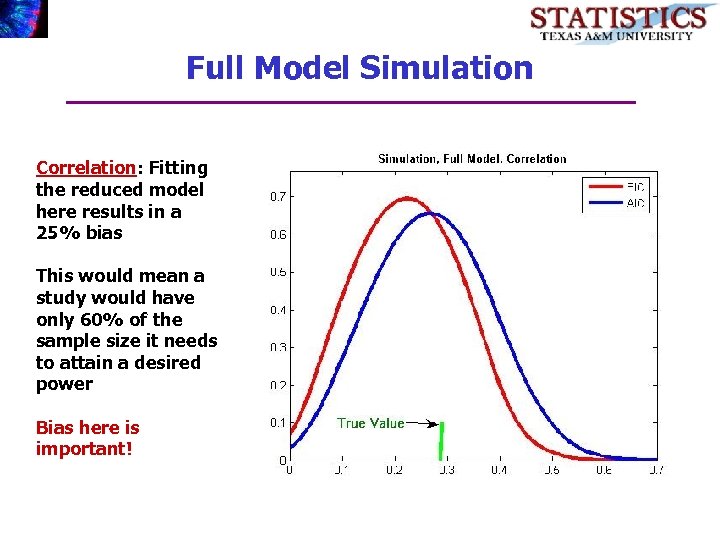Full Model Simulation Correlation: Fitting the reduced model here results in a 25% bias This would mean a study would have only 60% of the sample size it needs to attain a desired power Bias here is important!

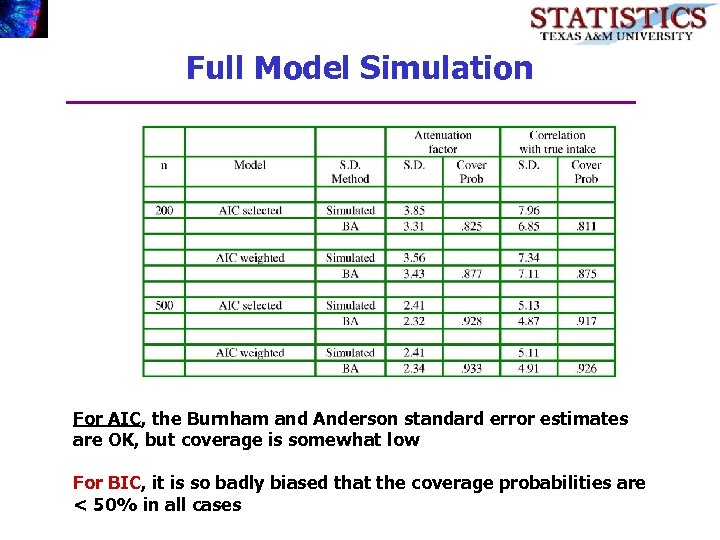Full Model Simulation For AIC, the Burnham and Anderson standard error estimates are OK, but coverage is somewhat low For BIC, it is so badly biased that the coverage probabilities are < 50% in all cases

Summary of Numerical Work § BIC: § seriously biased in the full model holds § Seems to love the reduced model § From the Biometrics article

Oracle Estimators § BIC: § This is an example of an oracle estimator § Leeb and Poetscher state

Oracle Estimators § Leeb and Poetscher go on to state § This seems to be too good to be true, and it is § It is a delusion to believe it carries statistical meaning § It is remarkable that some of the lessons learned from Hodges’ counterexample seem not to have been received in the model selection literature

Asymptotic Framework § I will next describe some local-alternative asymptotics for semiparametric models § These go some way to understanding the problem with oracle estimators § Semiparametric generalization of the work of Hjort and Claeskens

Semiparametric Framework § Likelihood Formulation § Example: Partially Linear Model

Semiparametric Framework § Example: Heteroscedastic Linear Model

Semiparametric Framework § Likelihood Formulation § Two models: § Full model § Reduced model

Semiparametric Framework § Local misspecification assumption § Intuitively: even an oracle will have to think a bit to distinguish between the full and reduced models § Practically: the models are not extremely different

Semiparametric Framework § Local misspecification assumption § Hjort and Claeskens: parametric models § We deal with semiparametric models

Profile Methods § Likelihood Formulation § For every , do local likelihood nonparametric regression to obtain § Then maximize

Semiparametric Information Bound § The semiparametric information is the semiparametric version of Fisher information § Many references, good one is Murphy and van der Vaart, JASA, 2002

Semiparametric Information Bound § Standard Result: For any function the full model , at

Semiparametric Information Bound § Non-Standard Result: we have to compute the limit distribution of the reduced model estimate at the full (local) model § Easy using contiguity arguments (Le. Cam’s 1 st, 2 nd and 3 rd Lemma)

Semiparametric Information Bound § Non-Standard Result: Note asymptotic bias

Semiparametric Information Bound § Model Averaging Result: Consider a model averaged estimator with weights for the reduced model depending on the profile likelihood, e. g. , BIC, AIC, etc. § Recall that § Let D be the limiting distribution of

Semiparametric Information Bound § Model Averaging Result: Then the model average estimator has limiting distribution § This is exactly the same result as in Hjort and Claeskens, except their Fisher information matrix is replaced by the semiparametric information bound

Semiparametric Information Bound § Inference: Hjort and Claeskens propose a method for inference that is asymptotically correct. § In numerous simulations and examples for AIC, we have found that it is essentially the same as fullmodel inference § BIC: In this local misspecification framework, BIC is an inconsistent model selector: it selects the reduced model with probability 1.

Summary § SUMEM: Model averaging can, in real life, result in estimators that decrease variance by 2/3 while retaining robustness § Very important in measurement error problems, where information is sparse § Inference: The Burnham and Anderson standard error formulae are reasonably precise § Because of non-normal limit distributions, coverage probabilities are much less than nominal

Summary § BIC and Oracles: Simply disastrous in our example § Lack of uniform consistency means the: “it sounds too good to be true” is correct § Bootstrap: Does not work § Not new, but striking numerics § Semiparametrics: § In the local framework, same as parametric methods with the semiparametric information bound replacing the Fisher information (I contiguity)

Burnham and Anderson Formula § You want to estimate a standard errror for a model-average estimate of

Bootstrap Problem § First two terms have same limit as the limit in the data world. § 3 rd term is not 0, hence inconsistency