Пример.ppt
- Количество слайдов: 28

Модель распределения работников по уровню заработной платы • • . Формирование заработной платы представляет собой мультипликативный процесс. На ее размер оказывает влияние различные факторы: образование, квалификация, общий стаж работы, педагогический стаж, использование новых технологий в образовательном процессе, количество и объем научных публикаций, интенсивность создания и освоения новых учебных курсов, количество и объем выпущенной учебной и учебнометодической литературы и другие.

Модель распределения работников по уровню заработной платы Сложность и многоплановость преподавательской деятельности обусловливает примерную равноценность множества факторов по их участию в формировании заработной платы, что дает основание предполагать логарифмически нормальное распределения анализируемого признака для однородной группы объектов. .

Модель распределения работников по уровню заработной платы • • В то же время, действие некоторых факторов, может приводить к существенным отличиям в уровне оплаты труда профессорско-преподавательского состава. К их числу можно отнести следующие: должность, ученая степень, ученое звание, преподавание как основной вид или не основной вид деятельности. Действие этих факторов обусловливает расслоение профессорско-преподавательского состава на дискретные страты в соответствие с традиционными представлениями о рассматриваемой сфере деятельности.

Модель распределения работников по уровню заработной платы • • • Отобраны Данные о заработной плате 496 преподавателей университета за 10 месяцев одного года в условных денежных единицах по следующим показателям: д – должность 1 – внешний, 2 – преподаватель, 3 – старший преподаватель, доцент, 4 – профессор, 5 - заведующий кафедрой; з – ученое звание 1 – доцент, 2 – профессор; с – ученая степень 1 – кандидат наук, 2 – доктор наук.

Модель распределения работников по уровню заработной платы Необходимо произвести классификацию преподавателей по уровню их заработной платы и охарактеризовать полученные классы (страты)

Модель распределения работников по уровню заработной платы Анализируемый признак – заработная плата – представляет собой результат совокупного действия множества факторов, среди которых отсутствуют явно доминирующие, характер действия факторов можно считать мультипликативным. вывод: для исследуемых объектов закон распределения признака логарифмически нормальный: где и - соответственно математическое ожидание и среднее квадратическое отклонение величины логарифма заработной платы.

Модель распределения работников по уровню заработной платы При наличии р - однородных групп сотрудников, существенно отличающихся друг от друга уровнем заработной платы, закон распределения будет представлять собой смесь р логарифмически-нормальных распределений. • где – доля объектов i– й группы в генеральной совокупности, • - плотность вероятности распределения i-й группы.
Модель распределения работников по уровню заработной платы Использование надстройки Excel «Гистограмма» для подтверждения теоретических предположений результатами анализа эмпирического распределения.
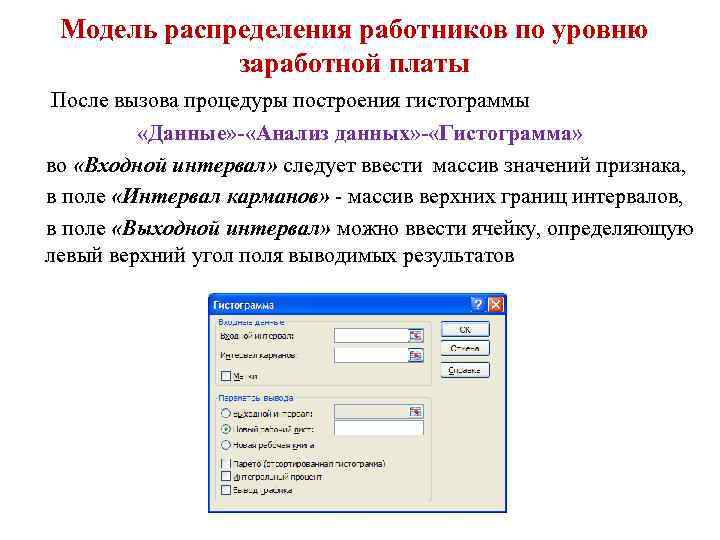
Модель распределения работников по уровню заработной платы После вызова процедуры построения гистограммы «Данные» - «Анализ данных» - «Гистограмма» во «Входной интервал» следует ввести массив значений признака, в поле «Интервал карманов» - массив верхних границ интервалов, в поле «Выходной интервал» можно ввести ячейку, определяющую левый верхний угол поля выводимых результатов

Модель распределения работников по уровню заработной платы Выбор интервалов, которые в Excel называются «карманами» , должен обеспечить: • наглядное отражение структуры распределения, • достаточное количество объектов, попадающих в каждый из интервалов. На предварительном этапе можно обойтись без указания «карманов» , после чего на основе визуального анализа полученной гистограммы построить ее окончательный вариант.

Модель распределения работников по уровню заработной платы Так как предполагается логарифмически-нормальное распределение заработной платы, гистограмму целесообразно строить по логарифму анализируемого признака. При этом границы интервалов тоже должны представлять собой логарифмы соответствующих значений.
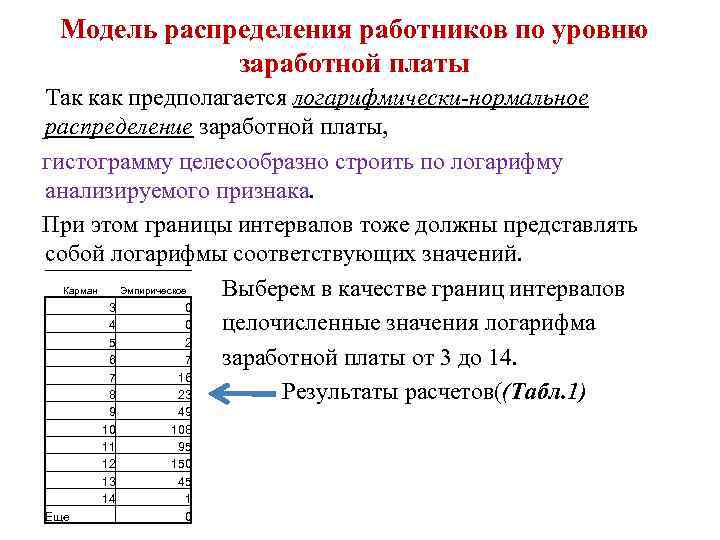
Модель распределения работников по уровню заработной платы Так как предполагается логарифмически-нормальное распределение заработной платы, гистограмму целесообразно строить по логарифму анализируемого признака. При этом границы интервалов тоже должны представлять собой логарифмы соответствующих значений. Карман Эмпирическое Выберем в качестве границ интервалов 3 0 4 0 целочисленные значения логарифма 5 2 6 7 заработной платы от 3 до 14. 7 16 8 23 Результаты расчетов((Табл. 1) 9 10 11 12 13 14 Еще 49 108 95 150 45 1 0
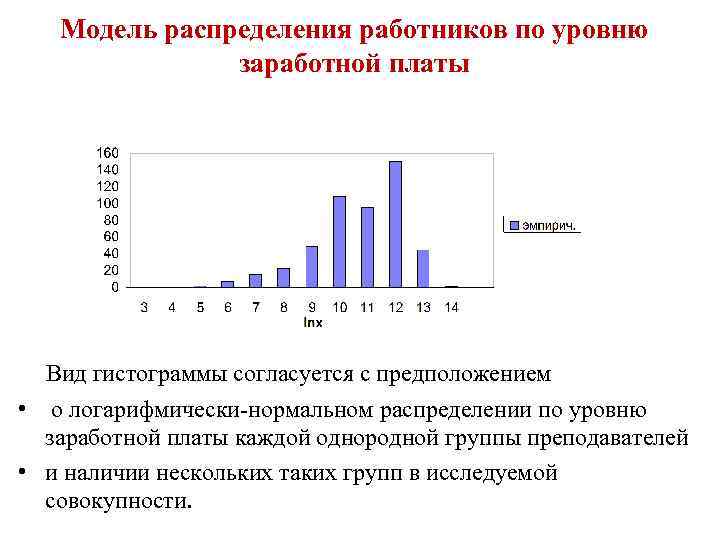
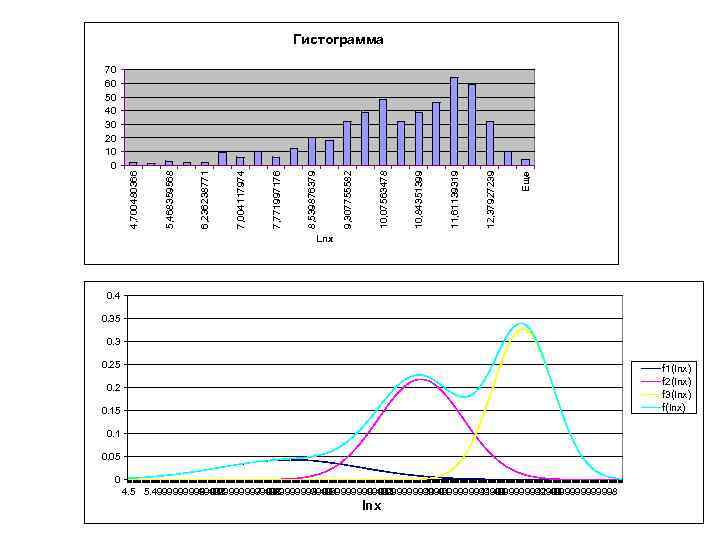
Модель распределения работников по уровню заработной платы Вид гистограммы согласуется с предположением • о логарифмически-нормальном распределении по уровню заработной платы каждой однородной группы преподавателей • и наличии нескольких таких групп в исследуемой совокупности.

Оценивание параметров закона распределения По полученной гистограмме логарифма заработной платы предположим • наличие трех страт с колообразными функциями распределения • визуально определим начальные приближения значений параметров Среднее значение для логарифма каждой страты определим приближенно как абсциссу точки ее предполагаемого максимума. Стандартное отклонение логарифма признака будет определяться расстоянием по оси абсцисс от предполагаемой точки максимума до точки перегиба плотности вероятности логарифма признака.
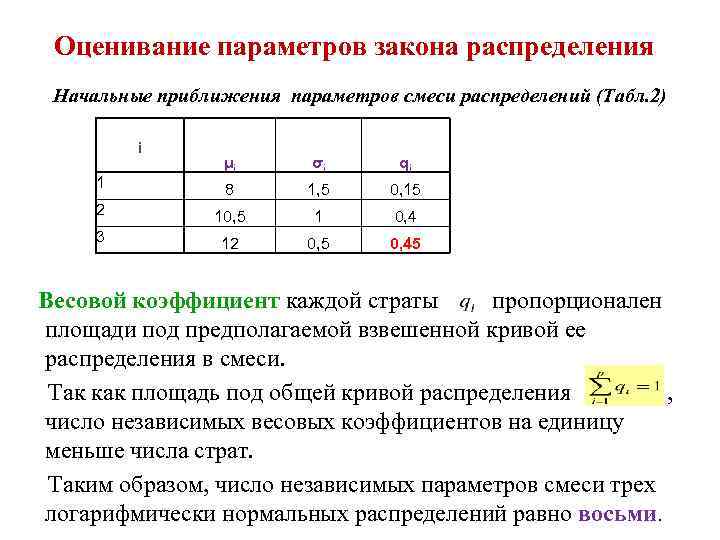
Оценивание параметров закона распределения Начальные приближения параметров смеси распределений (Табл. 2) i μi σi qi 8 1, 5 0, 15 2 10, 5 1 0, 4 3 12 0, 5 0, 45 1 Весовой коэффициент каждой страты пропорционален площади под предполагаемой взвешенной кривой ее распределения в смеси. Так как площадь под общей кривой распределения , число независимых весовых коэффициентов на единицу меньше числа страт. Таким образом, число независимых параметров смеси трех логарифмически нормальных распределений равно восьми.

Оценивание параметров закона распределения Теоретическую гистограмму можно построить по данным табл. 2, для выбранных ранее карманов (табл. 1). Для расчета используем функцию Excel ЛОГНОРМРАСП(x; среднее; стандартное_откл), которая возвращает интегральное логнормальное распределение, «Среднее» представляет собой среднее значение lnx для данного компонента смеси, то есть μi, а «Стандартное отклонение» - стандартное отклонение lnx, то есть σi. Таким образом, для расчета теоретической частоты первого (открытого) интервала можно использовать команду (ЛОГНОРМРАСП(exp(3); 8, 0; 1, 5)*0, 15+ЛОГНОРМРАСП(exp(3); 10, 5; 1, 0)*0, 4+ЛОГНОРМРАСП(exp(3); 12, 0; 0, 5)*0, 45)*496

Оценивание параметров закона распределения Расчет теоретических частот последующих закрытых интервалов предполагает вычисление накопленных частот для верхних границ и вычитание из них накопленных частот для нижних границ. Для второго интервала можно рекомендовать команду (ЛОГНОРМРАСП(exp(4); 8, 0; 1, 5)*0, 15+ЛОГНОРМРАСП(exp(4) ; 10, 5; 1, 0)*0, 4+ЛОГНОРМРАСП(exp(4); 12, 0; 0, 5)*0, 45)*496(ЛОГНОРМРАСП(exp(3); 8, 0; 1, 5)*0, 15+ЛОГНОРМРАСП(exp (3); 10, 5; 1, 0)*0, 4+ЛОГНОРМРАСП(exp(3); 12, 0; 0, 5)*0, 45)*496 Частоту конечного открытого интервала можно произвести с помощью команды 1(ЛОГНОРМРАСП(exp(14); 8, 0; 1, 5)*0, 15+ЛОГНОРМРАСП(ex p(14); 10, 5; 1, 0)*0, 4+ЛОГНОРМРАСП(exp(14); 12, 0; 0, 5)*0, 45)*4 96
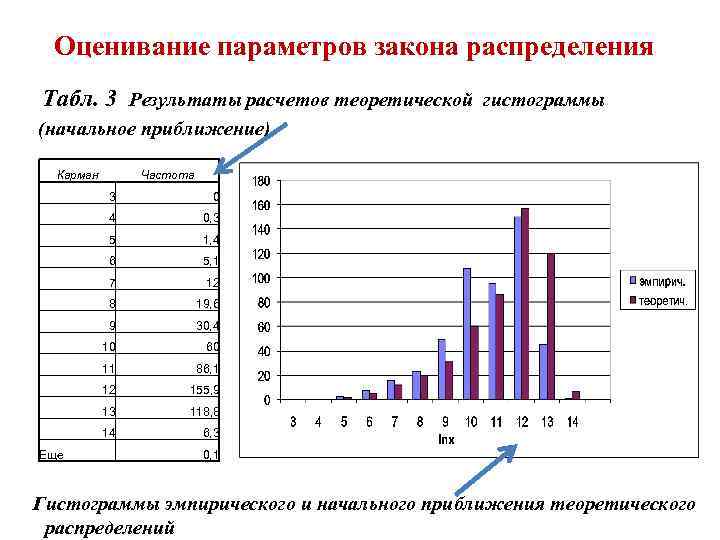
Оценивание параметров закона распределения Табл. 3 Результаты расчетов теоретической гистограммы (начальное приближение) Карман Частота 3 4 0, 3 5 1, 4 6 5, 1 7 12 8 19, 6 9 30, 4 10 60 11 86, 1 12 155, 9 13 118, 8 14 Еще 0 6, 3 0, 1 Гистограммы эмпирического и начального приближения теоретического распределений

Модель распределения работников по уровню заработной платы Существенное отличие гистограмм объясняется тем, что параметры, использованные для построения теоретического распределения, не являются оптимальными. Получение наилучших значений параметров требует • выбора критерия оптимальности • организации процедуры получения оценок. Использование критерия максимума правдоподобия. Он предусматривает использование в качестве оценок таких значений параметров, которые максимизируют многомерную плотность вероятности распределения признака для всей совокупности наблюдаемых значений, называемую функцией правдоподобия

Модель распределения работников по уровню заработной платы Для решения оптимизационной задачи удобно использовать надстройку «Поиск решения» в Excel. В качестве целевой ячейки следует указать ячейку с вычисляемым логарифмом отношения правдоподобия. Изменяемыми будут ячейки с задаваемыми значениями параметров (табл. 1). Ограничения позволят обеспечить выполнение условия , а также не допустить чрезмерного ухода параметров от первоначальных и попадания в точку локального максимума. T
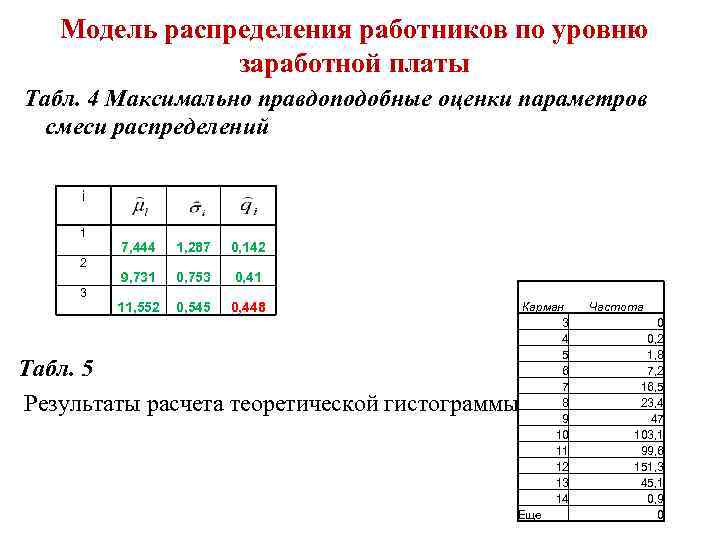
Модель распределения работников по уровню заработной платы Табл. 4 Максимально правдоподобные оценки параметров смеси распределений i 1 2 3 7, 444 1, 287 0, 142 9, 731 0, 753 0, 41 11, 552 0, 545 0, 448 Карман 3 4 5 6 7 8 9 10 11 12 13 14 Еще Табл. 5 Результаты расчета теоретической гистограммы Частота 0 0, 2 1, 8 7, 2 16, 5 23, 4 47 103, 1 99, 6 151, 3 45, 1 0, 9 0
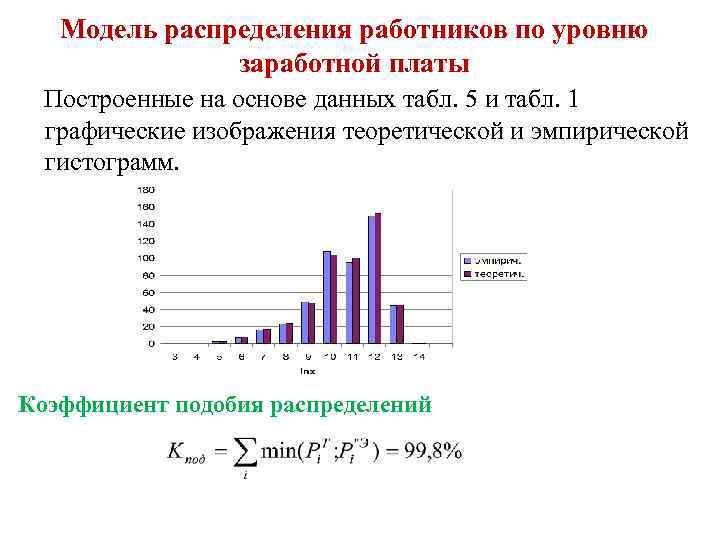
Модель распределения работников по уровню заработной платы Построенные на основе данных табл. 5 и табл. 1 графические изображения теоретической и эмпирической гистограмм. Коэффициент подобия распределений

Построение теоретического распределения и анализ результатов На основе полученных оценок строят модель смеси логарифмически нормальных распределений. Для этого формируют массив значений логарифма заработной платы с одинаковыми интервалами между соседними значениями. Число значений должно обеспечить необходимое качество графика плотности вероятности. Выберем сетку значений аргумента на интервале (4; 13, 5) с шагом 0, 02. Рассчитаем значения теоретической плотности вероятности, используя команду: Ссылки на соответствующие ячейки
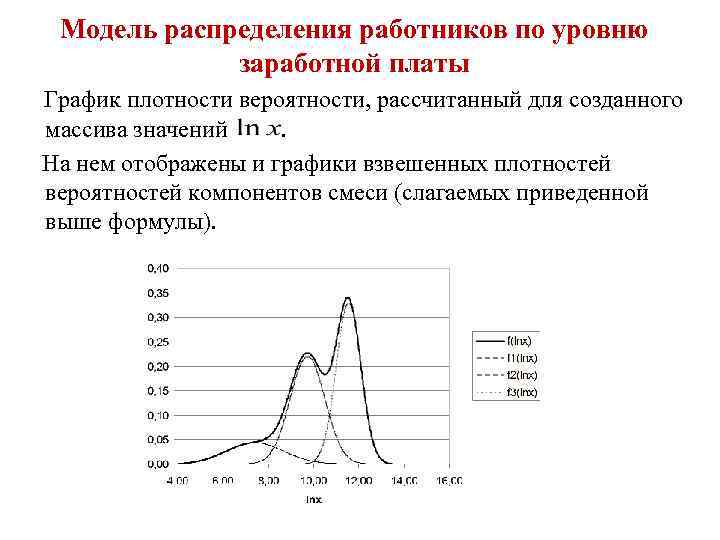
Модель распределения работников по уровню заработной платы График плотности вероятности, рассчитанный для созданного массива значений. На нем отображены и графики взвешенных плотностей вероятностей компонентов смеси (слагаемых приведенной выше формулы).
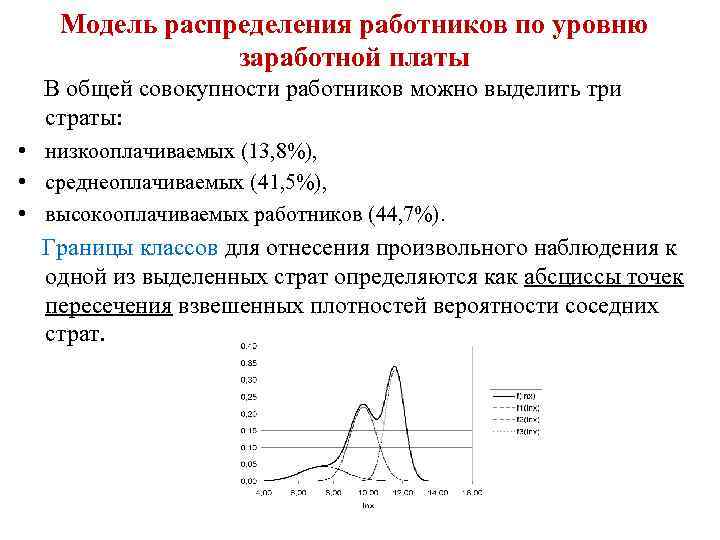
Модель распределения работников по уровню заработной платы В общей совокупности работников можно выделить три страты: • низкооплачиваемых (13, 8%), • среднеоплачиваемых (41, 5%), • высокооплачиваемых работников (44, 7%). Границы классов для отнесения произвольного наблюдения к одной из выделенных страт определяются как абсциссы точек пересечения взвешенных плотностей вероятности соседних страт.
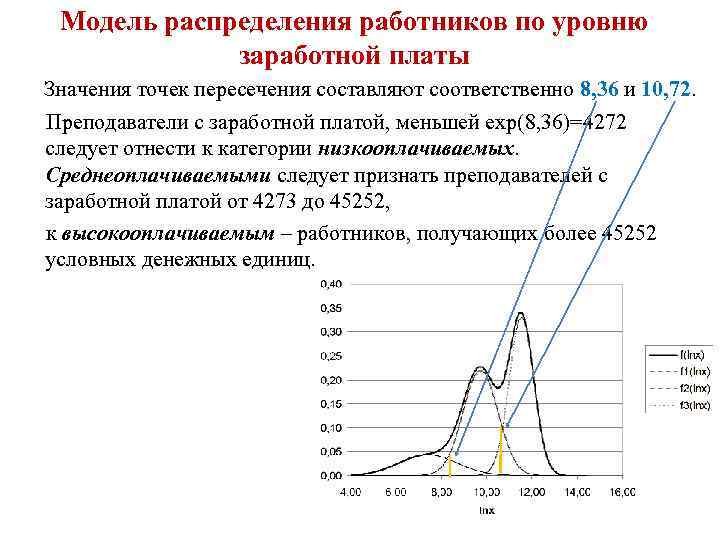
Модель распределения работников по уровню заработной платы Значения точек пересечения составляют соответственно 8, 36 и 10, 72. Преподаватели с заработной платой, меньшей exp(8, 36)=4272 следует отнести к категории низкооплачиваемых. Среднеоплачиваемыми следует признать преподавателей с заработной платой от 4273 до 45252, к высокооплачиваемым – работников, получающих более 45252 условных денежных единиц.
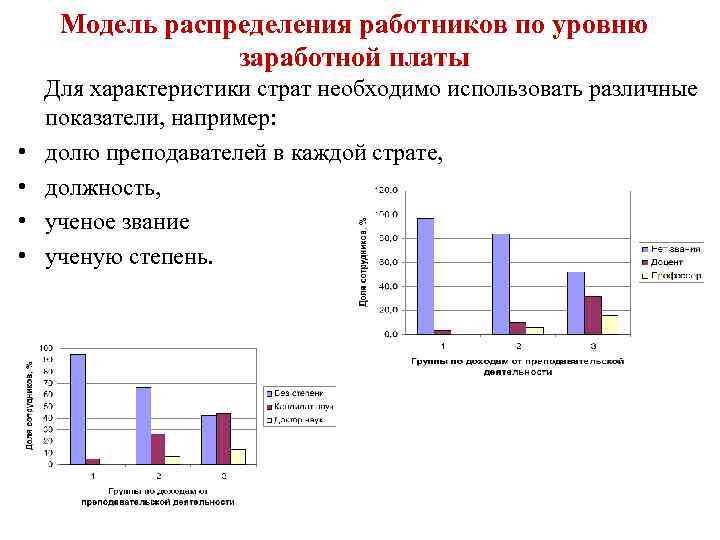
Модель распределения работников по уровню заработной платы • • Для характеристики страт необходимо использовать различные показатели, например: долю преподавателей в каждой страте, должность, ученое звание ученую степень.
Еще 12, 37927239 11, 61139319 10, 84351399 10, 07563478 9, 307755582 8, 539876379 7, 771997176 7, 004117974 6, 236238771 5, 468359568 70 60 50 40 30 20 10 0 4, 700480366 Гистограмма Lnx 0. 4 0. 35 0. 3 0. 25 f 1(lnx) f 2(lnx) f 3(lnx) f(lnx) 0. 2 0. 15 0. 1 0. 05 0 4. 5 5. 49999998 6. 49999996 7. 49999994 8. 49999993 9. 49999991 10. 4999999 11. 4999999 12. 49999998 lnx
Пример.ppt