Decision making for Gutin.pptx
- Количество слайдов: 29
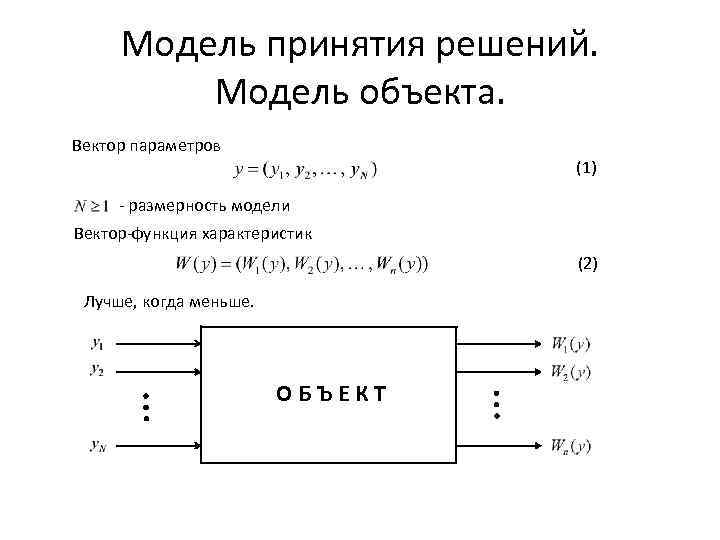
Модель принятия решений. Модель объекта. Вектор параметров (1) - размерность модели Вектор-функция характеристик (2) Лучше, когда меньше. ОБЪЕКТ

Модель принятия решений. Координатные ограничения. Координаты вектора изменяются в заданных пределах, определяемых векторами начала и конца (3) где - константы, причем , возможно Гиперпараллелепипед возможных значений вектора (4)

Модель принятия решений. Функциональные ограничения. Задается множество индексов (5) и набор допусков Для характеристик с номерами непревышения соответствующих допусков ставится условие т. е. вводятся функциональные ограничения (6) Определение. Вектор удовлетворяющий неравенствам (6), называется допустимым вектором (допустимой точкой).

Модель принятия решений. Функциональные ограничения. Введем обозначения (7) Тогда (8) Допустимая область (9) Если , то .

Модель принятия решений. Частичная вычислимость. Введем семейство вложенных множеств (10) Очевидно, что Определение. Ограничения (7) называются полностью вычислимыми, если все функции определены и вычислимы в множестве Определение. Ограничения (7) называются частично-вычислимыми, если каждая функция соответствующем множестве определена и вычислима в

Модель принятия решений. Векторный критерий эффективности. Зададим множество индексов (11) и введем вектор-функцию (12) где (13) Вектор-функция (12) называется векторным критерием эффективности. В модели с частичной вычислимостью все частные критерии могут быть определены только в области В общем случае допускается

Модель принятия решений. Оптимальность решения. Решение оптимизационной задачи (14) принимается в качестве оптимального решения в рамках сформированной модели.

Модель принятия решений. Консервная банка.
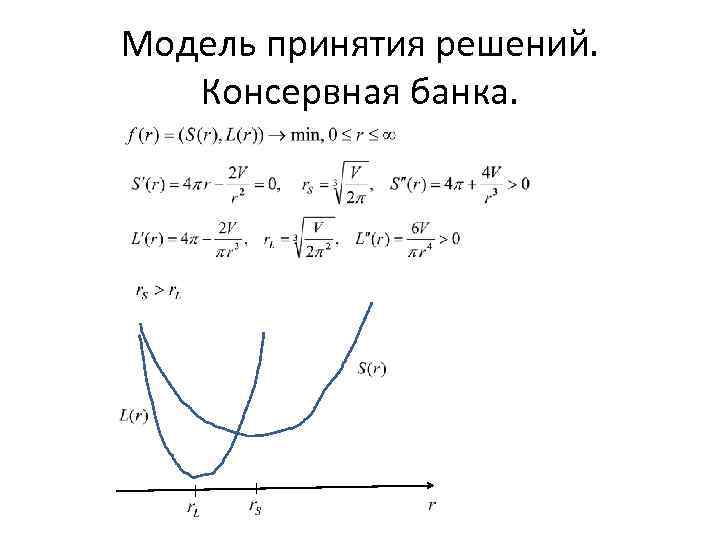
Модель принятия решений. Консервная банка.

Модель принятия решений. Оптимальное решение Что является оптимальным решением в случае противоречивости частных критериев?

Модель принятия решений. Оптимальное решение Определение 1. Точка доминирует точку , если (сильное доминирование). Определение 2. Точка и существует номер (слабое доминирование). доминирует точку такой, что , если

Модель принятия решений. Паретовское оптимальное решение. Определение 3. Точка и соответствующий ей вектор называются эффективными (неулучшаемыми, оптимальными по Парето), Если из условий следует, что . оптимальна по Парето, если ее нельзя улучшить в частному критерию. Оптимальное решение – множество ни по одному всех паретовских точек.

Модель принятия решений. Слейтеровское оптимальное решение. Определение 4. Точка называется слабо эффективной (оптимальной по Слейтеру, слейтеровской точкой), если не существует такой, что (т. е. не существует доминатора в смысле Определения 1). Оптимальное решение – множество Очевидно, что . всех слейтеровских точек.

Метод главного критерия . . .

Метод сверток. Линейная свертка. Вектор весов Линейная свертка Рассмотрим задачу
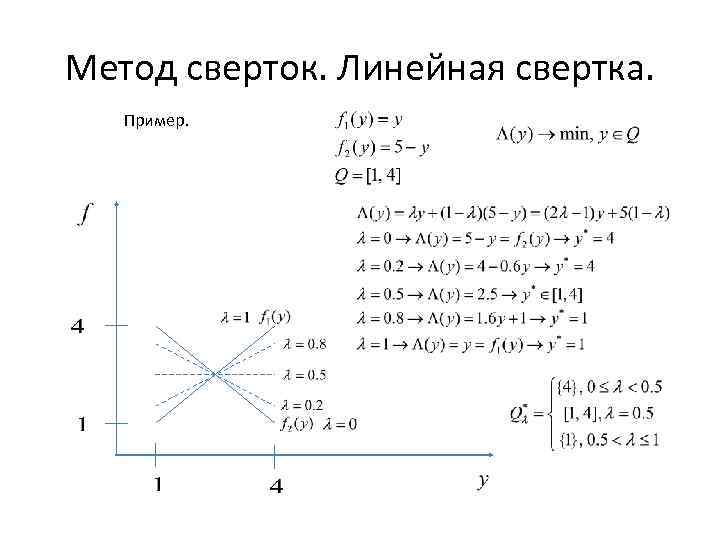
Метод сверток. Линейная свертка. Пример.
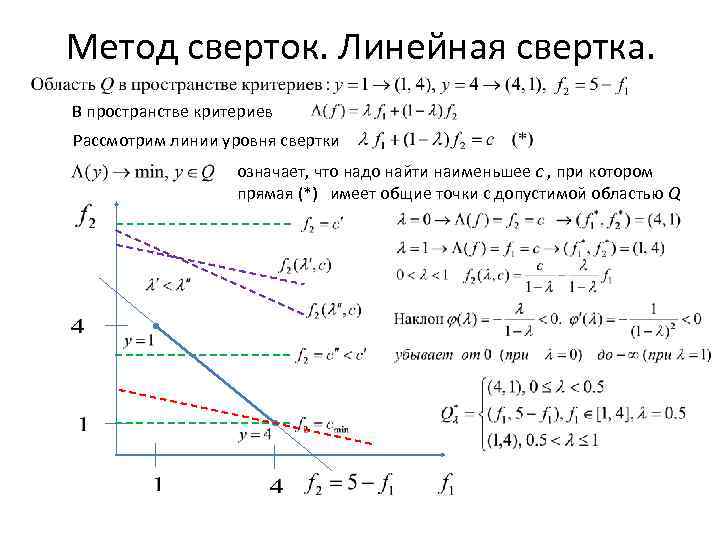
Метод сверток. Линейная свертка. В пространстве критериев Рассмотрим линии уровня свертки означает, что надо найти наименьшее c , при котором прямая (*) имеет общие точки с допустимой областью Q
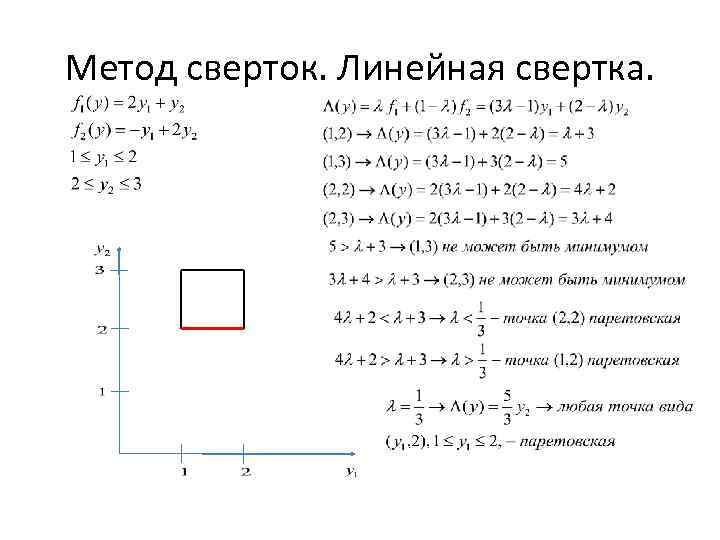
Метод сверток. Линейная свертка.
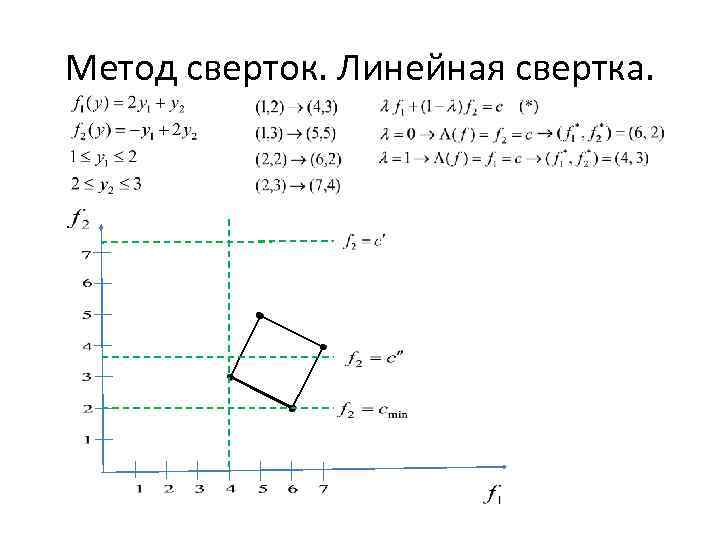
Метод сверток. Линейная свертка.
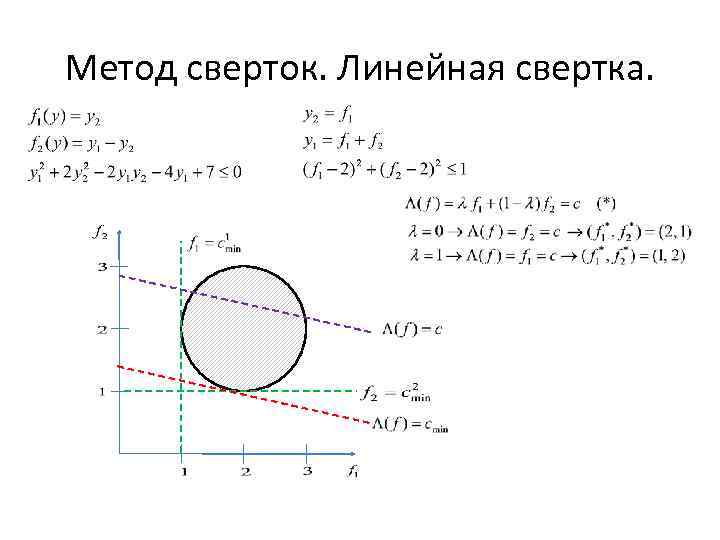
Метод сверток. Линейная свертка.
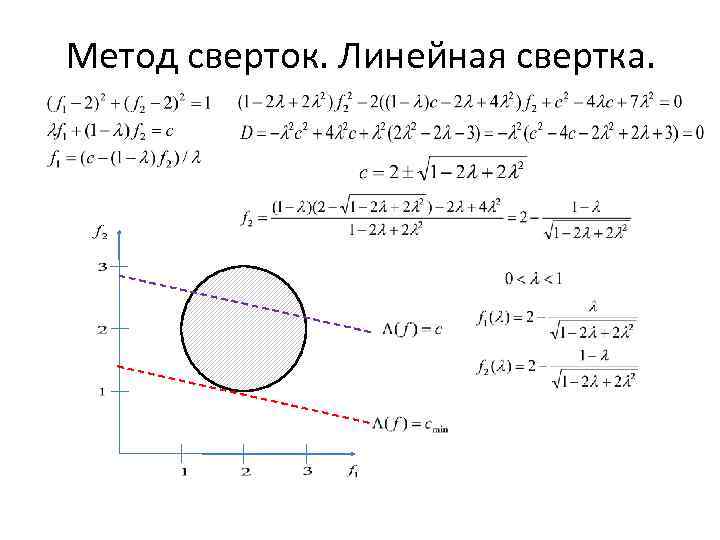
Метод сверток. Линейная свертка.

Метод сверток. Свертка Гермейера. Вектор весов Свертка Гермейера Пусть Решение задачи является слейтеровским решением многокритериальной задачи

Геометрическая интерпретация свертки Гермейера.
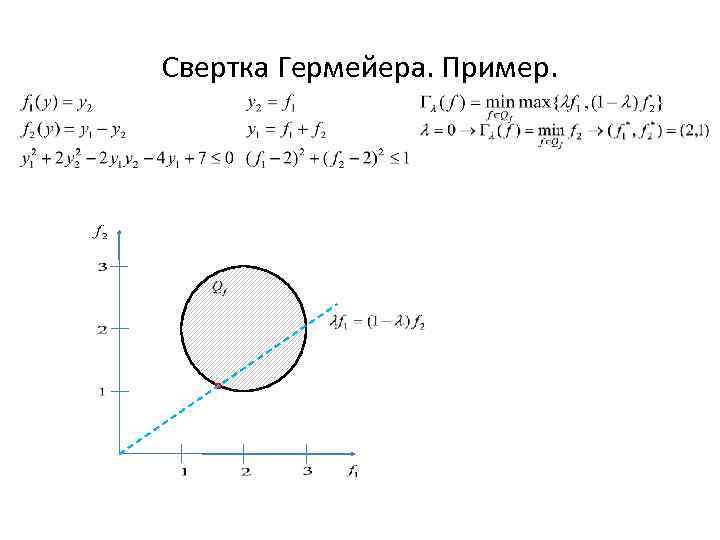
Свертка Гермейера. Пример.
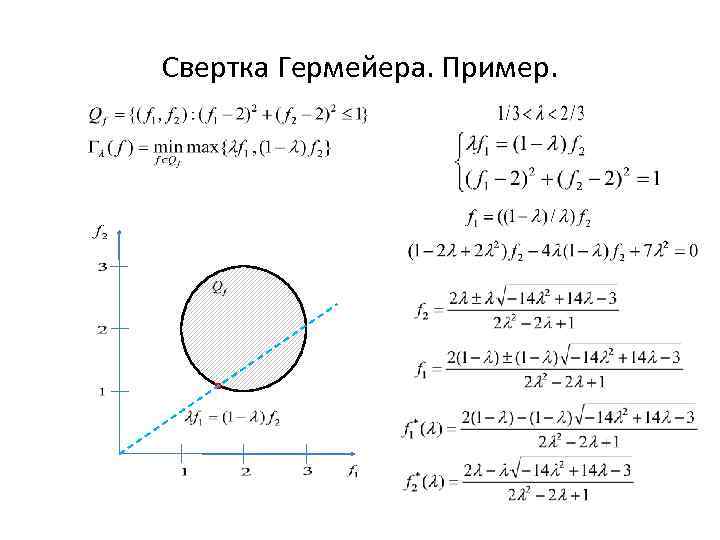
Свертка Гермейера. Пример.

Метод уступок Упорядочиваем по важности

Метод уступок. . . Точка - глобальный минимум последней задачи – паретовская.

Многокритериальные задачи. Примеры. ______________________________

Многокритериальные задачи. Примеры.
Decision making for Gutin.pptx