Модель оптимального планирования L O G O www themegallery com

Модель оптимального планирования L/O/G/O www. themegallery. com

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОПТИМИЗАЦИИ ПРОИЗВОДСТВА Умение строить планы на различном уровне, для разных целей – это важное, но не достаточное условие наилучшего функционирования экономических систем различной степени сложности, различного уровня и различного масштаба. Надо не просто уметь строить планы, главное – уметь выбирать из них один, наилучший (оптимальный из всех допустимых).

Иными словами, следует пользоваться принципом оптимальности, который в самом простом виде можно выразить следующим образом: есть цель, ради которой строится план (критерий оптимальности или целевая функция), и есть условия, при которых может быть достигнута эта цель (ограничения).

Математический аппарат – математическое программирование. Линейное программирование решает задачи на достижение максимума (минимума) линейной функции с линейными ограничениями.

При попытке оптимизации любой экономической системы на любом уровне экономической иерархии встречаемся с целым рядом трудностей: 1 Сложность экономической системы 2 Большое число факторов, влияющих на ее развитие 3 Постоянная изменчивость ее компонентов 4 Влияние случайных факторов В большинстве случаев стараются свести все задачи оптимизации к линейному варианту, к линейным функциям.

Линейная статическая модель оптимального планирования Рассматривая новую модель, для лучшего понимания материала будем сравнивать её с моделью межотраслевого баланса производства и распределения продукции является то, что вместо единственного столбца коэффициентов затрат каждому виду продукции может соответствовать несколько способов, отражающих затраты при различных технологических (производственных) способах получения этой продукции.

Технологические способы могут входить в план с различной интенсивностью, в т. ч. и нулевой. При этом допустимым вариантом плана будет любой набор интенсивностей применения технологических способов, при котором выполняются исходные ограничения модели. Среди допустимых вариантов должен быть найден наиболее эффективный, поэтому исключительное значение приобретает вопрос о показателе, по которому оценивается эффективность вариантов и отбирается наилучший, т. е. вопрос о критерии оптимальности плана. Остановимся на одном возможном критерии (простейшем). Будем считать целью оптимального планирования достижение максимального объема конечной продукции при заданной ее структуре.

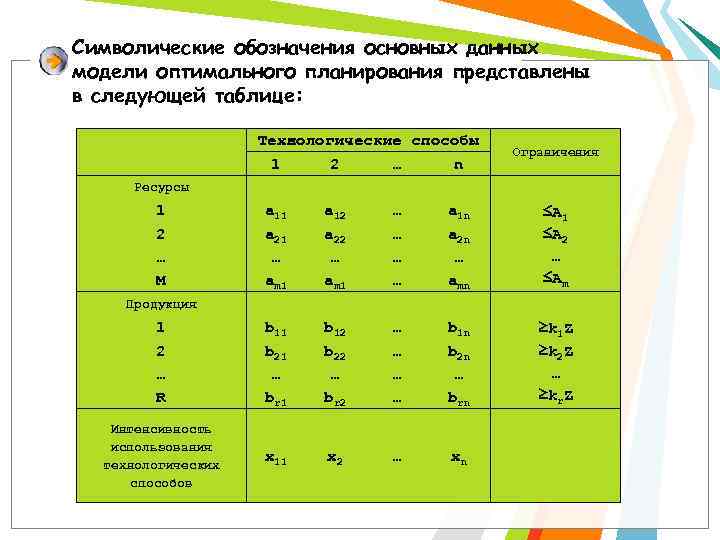Символические обозначения основных данных модели оптимального планирования представлены в следующей таблице: Технологические способы 1 2 … n Ограничения Ресурсы 1 2 … M a 11 a 21 … am 1 a 12 a 22 … am 1 … … a 1 n a 2 n … amn ≤А 1 ≤А 2 … ≤Аm 1 2 … R b 11 b 21 … br 1 b 12 b 22 … br 2 … … b 1 n b 2 n … brn ≥k 1 Z ≥k 2 Z … ≥kr. Z Интенсивность использования технологических способов x 11 x 2 … xn Продукция

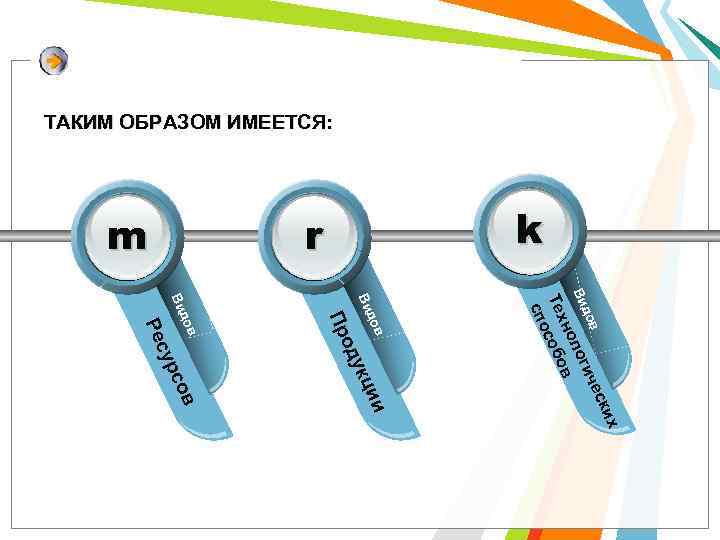ТАКИМ ОБРАЗОМ ИМЕЕТСЯ: k r m в ких ии сов укц ес в до гич Ви ло но в Тех собо спо до Ви од Пр в до Ви сур Ре

Заданы коэффициенты k 1, k 2, . . , kr aij bij - доля каждого вида в общем объеме конечной продукции Z. - показывают, сколько единиц ресурса i-го вида затрачивается при j-м технологическом способе, если способ используется один раз или с единичной интенсивностью, i=1, …, m; j=1, …, n. - показывают, сколько единиц продукции i-го вида выпускается при j-м технологическом способе, если способ используется один раз или с единичной интенсивностью. max Z (общий объем конечной продукции)

Смысл задачи в рамках данной модели следующий: с какой интенсивностью следует использовать каждый технологический способ, чтобы получить максимальный объем конечной продукции Z при заданной его структуре и заданных ограничениях по ресурсам и продукции.