Модель оцінки капітальних активів МОКА Сapital Asset Pricing

Модель оцінки капітальних активів (МОКА) Сapital Asset Pricing Model — CАРМ Розроблена у середині 60 -х рр. Уільямом Шарпом та Дж. Лінтерном. Застосування САРМ дає змогу значно обмежити кількість вхідних параметрів. Наприклад, за умови залучення 100 різних видів фінансових активів для моделі Марковіца слід обчислити 4950 параметрів, для моделі Шарпа — лише 201.

Народився 16 червня 1934 р. (79 років) у м. Бостон, Массачусетст, США. Американський економіст. Лауреат нобелевської премії 1990 року “за работи з теорії фінансової економіки”. Закінчив Каліфорнійський університет (Лос-Анжелес), там же отримав ступінь доктора. Уільям Шарп Викладав в університеті штату Вашингтон, Каліфорнійському і Стенфордському університетах.

Портфель інвестора складається з безризикового активу та ринкового портфеля. Ринковий портфель - це портфель, що з усіх фінансових інструментів, наявних на ринку, питома вага яких дорівнює їх питомій вазі у сукупній вартості фінансових інструментів на ринку. У всіх покупців цінних паперів структура попиту однакова. Хоча розміри портфелів у інвесторів різні, всі вони хочуть мати однаковий асортимент ризикових активів. Для забезпечення рівноваги на ринку ризикових цінних паперів структура пропозиції цінних паперів збігається зі структурою ринкового портфеля.

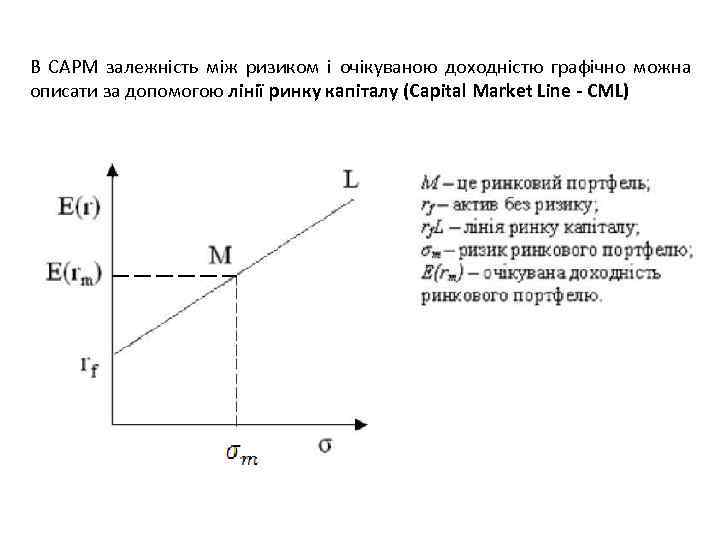В САРМ залежність між ризиком і очікуваною доходністю графічно можна описати за допомогою лінії ринку капіталу (Capital Market Line - CML)

СМL є прямою лінією, рівняння якої можна представити як: у = а + вх, де: а - значення ординати в точці перетину її лінією СМL, що відповідає ставці без ризику в - кут нахилу СМL. Кут нахилу визначається як відношення зміни значення функції до зміни аргументу:

Модель САРМ встановлює залежність між ризиком активу (портфеля) і його очікуваною дохідністю. Лінія ринку капіталу (CML) показує залежність між ризиком широко діверсифікованого портфеля, вимірюваним дисперсією, і його очікуваною дохідністю.

Очікувана доходність портфеля дорівнює ставці без ризику плюс добуток відношення ризику активу (портфеля) до ризику ринкового портфеля і різниці між очікуваною дохідністю ринкового портфеля і ставкою без ризику. Приклад 1. Визначити очікувану дохідність портфеля: 25 % Приклад 2. 10 % 15 % 20 %

У чому різниця між ринковим та неринковим ризиком? Ризик, з яким пов’язане володіння активом, можна поділити на дві частини. Перша складова - це ринковий ризик. Його також називають системним або недиверсифікованим (неспецифічним). Він пов’язаний із станом кон’юнктури ринку, загальнозначущими подіями (війною, революцією тощо). Друга складова - неринковий, специфічний або диверсифікований ризик. Він пов’язаний з індивідуальними властивостями конкретного активу, а не зі станом ринку в цілому. Широко диверсифікований портфель включає в себе практично лише ринковий ризик. Слабко диверсифікованому портфелю притаманні як ринкоий, так і неринковий ризики. Таким чином, інвестор може знизити свій ризик лише до рівня ринкового, якщо сформує широко диверсифікований портфель.

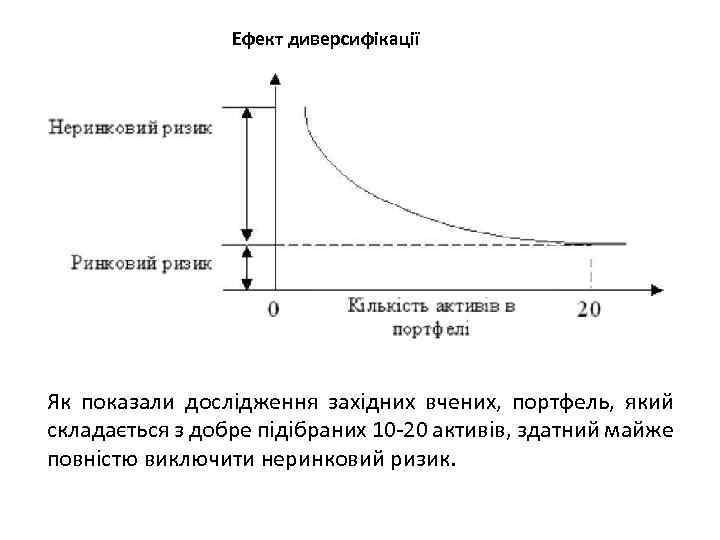Ефект диверсифікації Як показали дослідження західних вчених, портфель, який складається з добре підібраних 10 -20 активів, здатний майже повністю виключити неринковий ризик.

Для вимірювання ринкового ризику активу (портфеля) використовується величина бета. Вона показує залежність між прибутковістю активу (портфеля) і прибутковістю ринку. Доходність ринку - це доходність ринкового портфеля. Оскільки неможливо сформувати портфель, в який би входили всі фінансові активи, то в якості нього приймається будь-який індекс з широкою базою. Тому доходність ринку - це доходність портфеля, представленого обраним індексом. Величина активу (портфеля) без ризику дорівнює нулю, тому що нулю дорівнює коваріація доходності активу (портфеля) без ризику з доходністю ринкового портфелю. Величина активу (портфеля) показує, наскільки його ризик більше або менше ризику ринкового портфелю. Активи з більше одиниці є більш ризиковими, а з менше одиниці - менш ризиковими, ніж ринковий портфель. Якщо активу дорівнює одиниці, то його ризик дорівнює ризику ринкового портфелю.

Величина може бути додатньою, так і від’ємною. Додатнє значення свідчить про те, що доходності активу (портфеля) і ринку при зміні кон’юнктури змінюються в одному напрямку. Від’ємна показує, що дохідності активу (портфеля) і ринку змінюються в протилежних напрямках. Наприклад, цінного паперу дорівнює +2. Це означає, що при збільшенні очікуваної дохідності ринкового портфелю на 1 % доходність цінного паперу зросте на 2 %, і навпаки, при зменшенні доходності ринкового портфелю на 1 % доходність цінного паперу знизиться на 2 %.

Оскільки цінного паперу більше одиниці, то вона є більш ризиковою, ніж ринковий портфель. Якщо цінного паперу дорівнює 0, 5, то при збільшенні очікуваної доходності ринку на 1 % очікувана доходність паперу повинна зрости тільки на 0, 5 %. І навпаки, при зниженні доходності ринку на 1 % доходність цінного паперу зменшиться тільки на 0, 5 %. Таким чином, ризик даного цінного паперу менше ризику ринку. Якщо дорівнює -2, то при підвищенні доходності ринкового портфелю на 1 % доходність активу зменшиться на 2 % і, навпаки. Активи з від’ємною є цінними інструментами для диверсифікації портфелю, оскільки в даному випадку можна побудувати портфель з “нульовою ”, який не буде ризиковим. Однак потрібно пам’ятати, що такий портфель не аналогічний активу без ризику, так як при нульовому значенні він не містить тільки систематичного ризику. У той же час даний портфель збереже неринковий ризик.

Знаючи величину для кожного з активів, вкладник може легко сформувати портфель необхідного рівня ризику та доходності. портфеля - це середньозважене значення величин активів, що входять в портфель, де вагою виступає їх частка в портфелі. Вона розраховується за формулою: кожного активу розраховується на підставі доходності активу і ринку за попередні періоди часу. Інформацію про значення можна одержати від аналітичних компаній, які займаються аналізом фінансового ринку, а також з періодичної преси. Приклад. Інвестор формує портфель з трьох активів: А, В и С. βа = 0, 8; βв = 0, 95; βс = 1, 3; θа = 0, 5; θв = 0, 2; θс = 0, 3. β портфеля дорівнює: 0, 5 • 0, 8 + 0, 2 • 0, 95 + 0, 3 • 1, 3 = 0, 98.

Про що говорить бета активу? Якщо бета активу дорівнює нулю, чи означає це, що він є безризиковим? Портфель складається з п'яти активів. Питома вага і першого активу дорівнюють відповідно 20 % та 0, 5, другого – 20 % і 0, 8, третього – 40 % і 1, четвертого – 10 % і 1, 2, п'ятого – 10 % і 1, 4. Визначити портфеля. (Відповідь: 0, 92) Портфель складається з двох акцій - А і В. Питома вага акції А в портфелі дорівнює 30 %, = 0, 8, неринковий ризик – 15 %. Питома вага акції В дорівнює 70 %, = 1, 3, неринковий ризик – 8 %. Ринковий ризик дорівнює 10 %. Чому дорівнює весь ризик портфеля, представлений стандартним відхиленням? (Відповідь: 13, 5%)

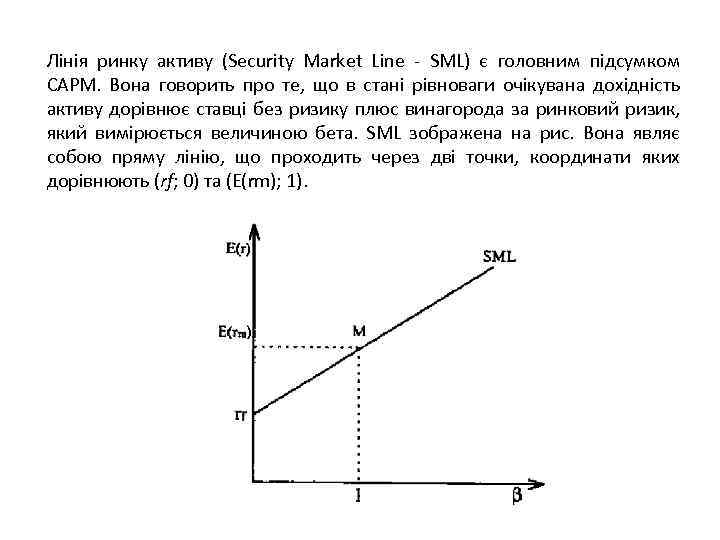Лінія ринку активу (Security Market Line - SML) є головним підсумком САРМ. Вона говорить про те, що в стані рівноваги очікувана дохідність активу дорівнює ставці без ризику плюс винагорода за ринковий ризик, який вимірюється величиною бета. SML зображена на рис. Вона являє собою пряму лінію, що проходить через дві точки, координати яких дорівнюють (rf; 0) та (E(rm); 1).

Очікувану прибутковість активу (портфеля) визначають за допомогою рівняння SML. Приклад. rf = 15 %, E(rm) = 25 %, = 1, 5. Визначити E(ri). 15 % + 1, 5 (25 %− 15 %) = 30 % Ставка без ризику 10 %, очікувана дохідність ринку – 20 %, бета портфеля акцій - 0, 8. Визначте очікувану прибутковість портфеля. (Відповідь: 18%)

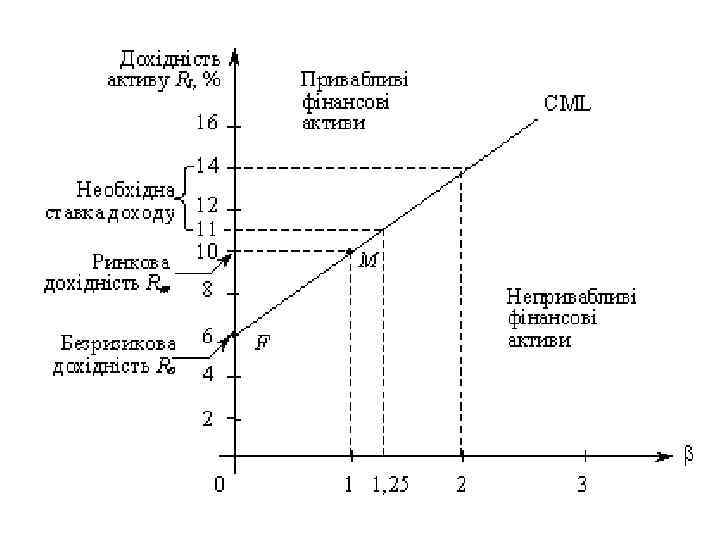
Графічне відображення САРМ — лінію ринку капіталу CML можна побудувати, враховуючи, що вона увиразнює компроміс між дохідністю і ризиком для ефективних портфелів. Якщо -коефіцієнт дорівнює 0, очікувана дохідність дорівнює дохідності безризикових активів (6 %), а якщо 1 — ринковій дохідності 10 %. На підставі зазначених даних отримують дві крапки на графіку (F і M), через які проводять пряму лінію Capital Market Line CML, що демонструє, якою мірою зростання ризику збільшується очікувана дохідність. Очікувана дохідність активу (необхідна ставка доходу), наприклад, дорівнюватиме 11 %, коли дорівнює 1, 25. Якщо збільшити до 2, дохідність становитиме 14 %.

Розглянемо застосування САРМ на конкретному прикладі. Інвестиція є прийнятною для інвестора, якщо дохідність фінансового активу становитиме не менше 14 %. Визначимо доцільність альтернативи інвестування коштів в акції компанії Z, яка має = 1, 6, або компанії Q, що має = 0, 9. Безризикова дохідність Rо = 6 %, середня дохідність ринку Rm = 12 %. Очікувана дохідність акцій для компанії Z: = 0, 06 + 1, 6 (0, 12 - 0, 06) = 0, 156; для компанії Q = 0, 06 + 0, 9 (0, 12 - 0, 06) = 0, 114. На підставі розрахунків доходимо висновку, що інвестиція доцільна в акції компанії Z. Взаємозв’язок розглянутих показників графічно можна продемонструвати лінією ринку капіталів.

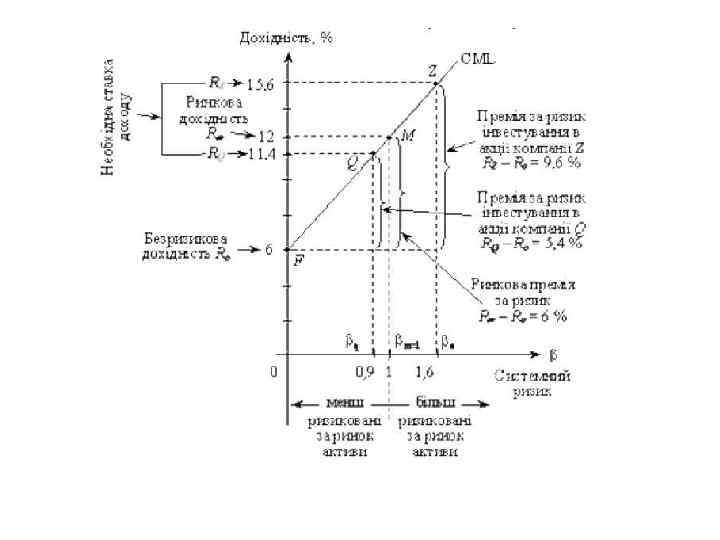
Як випливає з САРМ, кожному фінансовому активу відповідає точка на рисунку. Можливі три варіанти розташування цієї точки: на лінії ринку капіталів, вище або нижче цієї лінії. У другому разі актив вважають інвестиційно привабливим, у третьому — не привабливим. Можливі й інші способи використання лінії ринку капіталів. Якщо безризикова ставка 0, 06, середня за (фондовим індексом) дохідність ринку — 0, 12, а -коефіцієнт акції — 1, 2, необхідна ставка доходу і-го фінансового активу дорівнює Rі = 0, 06 + 1, 2 (0, 12 - 0, 06) = 0, 132. Це означає, що акції з ризиком = 1, 2 мають забезпечити дохідність, не меншу за 13, 2 %. Якщо дохідність акцій менша, їх треба позбутися, якщо вища — має сенс залучити до портфеля. Якщо Rі (необхідну ставку доходу) розраховують на майбутній період, дохідність дисконтують за цією ставкою.

Як безризикову ставку під час практичних досліджень обирають, як правило, дохідність за короткотерміновими (від трьох місяців до року) державним зобов’язанням, облікову ставку (або ставку рефінансування) центрального банку, або розраховану визначеним способом середньозважену ставку за кредитами на міжбанківському ринку (наприклад, ставку LIBOR — London Interbank Offered Rate). Для розрахунку ринкової дохідності використовують фондові індекси, які вимірюють середньозважений рівень цін за певною групою активів. Серед аналітиків тривають суперечки щодо сутності фондових індексів. Дехто з них взагалі заперечує можливість визначення на їх підставі середніх ринкових показників для САРМ. Утім, практики вже мають достатній позитивний досвід застосування індексів Standart and Poor’s (SP-500) та інших фондових індексів за умови залучення до їх обчислення ринкових цін великої кількості цінних паперів. Приріст фондового індексу за конкретний період — це середньозважений капітальний дохід за цінними паперами, ціни на які використано під час розрахунку індексу. Проте за багатьма цінними паперами капітальний дохід — це лише одна складова загального доходу. Так, за акціями також виплачують дивіденди, за облігаціями — відсотки. Крім того, доходи, отримані впродовж певного періоду, можуть бути реінвестовані. За наявності потрібної інформації можна врахувати також середньозважені проміжні доходи за цінними паперами.

Альфа - це показник, який характеризує величину невірної оцінки дохідності активу ринком у порівнянні з рівноважним рівнем його дохідності. Позитивне значення альфи свідчить про його недооцінку, негативне - переоцінку. Альфа визначається за формулою: Альфа являє собою різницю між дійсною дохідністю актива і рівноважною дохідністю, тобто дохідністю, яку вимагає ринок для даного рівня ризику .

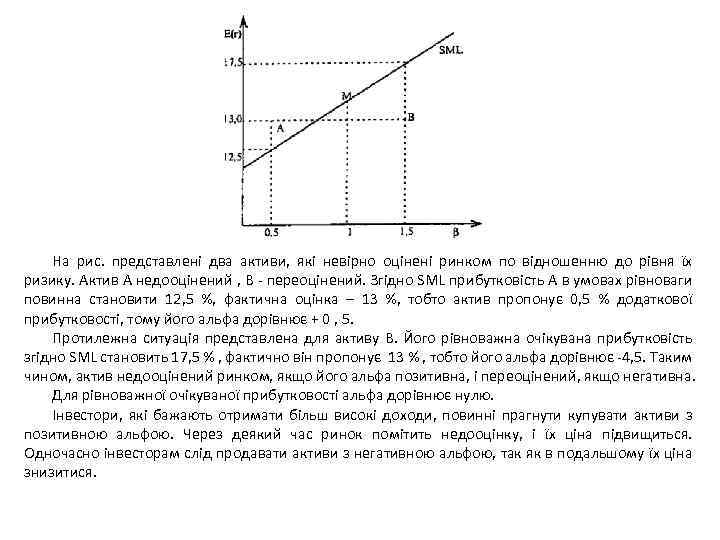На рис. представлені два активи, які невірно оцінені ринком по відношенню до рівня їх ризику. Актив А недооцінений , В - переоцінений. Згідно SML прибутковість А в умовах рівноваги повинна становити 12, 5 %, фактична оцінка – 13 %, тобто актив пропонує 0, 5 % додаткової прибутковості, тому його альфа дорівнює + 0 , 5. Протилежна ситуація представлена для активу В. Його рівноважна очікувана прибутковість згідно SML становить 17, 5 % , фактично він пропонує 13 % , тобто його альфа дорівнює -4, 5. Таким чином, актив недооцінений ринком, якщо його альфа позитивна, і переоцінений, якщо негативна. Для рівноважної очікуваної прибутковості альфа дорівнює нулю. Інвестори, які бажають отримати більш високі доходи, повинні прагнути купувати активи з позитивною альфою. Через деякий час ринок помітить недооцінку, і їх ціна підвищиться. Одночасно інвесторам слід продавати активи з негативною альфою, так як в подальшому їх ціна знизитися.

Дохідність портфеля - це середньозважена величина дохідностей активів що входять до нього, тому альфа портфеля також є середньозваженою величиною і визначається за формулою: - альфа портфеля; - питома вага і-того актива у портфелі; - альфа і-того актива. Приклад. Портфель складається з трьох цінних паперів — А, В і С. αА = 2; αв = 1, 5; αс = -1; θА = 0, 5; θв = 0, 2 і θс = 0, 3. Альфа такого портфеля дорівнює: 0, 5 • 2 + 0, 2 • 1, 5 + 0, 3 • (− 1) =1

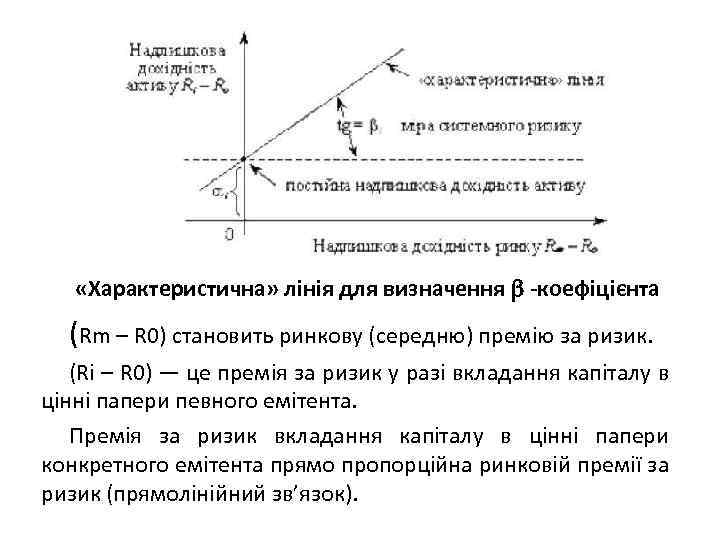«Характеристична» лінія для визначення -коефіцієнта (Rm – R 0) становить ринкову (середню) премію за ризик. (Ri – R 0) — це премія за ризик у разі вкладання капіталу в цінні папери певного емітента. Премія за ризик вкладання капіталу в цінні папери конкретного емітента прямо пропорційна ринковій премії за ризик (прямолінійний зв’язок).

Під час використання портфельної теорії найпростішим і найчастіше застосовуваним на практиці підходом до розрахунку очікуваної дохідності й міри ризику є розрахунок на підставі історичних значень. Значення в визначають на підставі пошуку параметрів регресивної моделі «характеристичної» лінії ( «Characteristic» Line) типу Ri - Rо = аі + i (Rm - Rо), де Ri — дохідність і-го цінного папера, Rо — безризикова ставка доходу, αі — постійна надлишкова дохідність активу, Rm — середньоринкова дохідність, i— тангенс кута нахилу, міра системного ризику. Ця модель визначає залежність між надлишковою дохідністю (премією за ризик) і-го цінного папера (Ri - Rо) і надлишковою дохідністю ринку (Rm - Rо). Значення αі може бути більшим і меншим за 0. Чим вище α, тим привабливіша акція. Якщо α > 0, актив недооцінено, якщо α < 0, актив переоцінено. За американським висловом: «keep your α high and low» (дотримуйся високого α і низького ). Для спрощення розрахунків α і на практиці застосовується модель типу Ri = αі + βіRm, де Ri — дохідність і-го цінного папера, Rm — дохідність ринку, αі, і —відповідні параметри.

Визначте альфу активу, якщо його рівноважна очікувана дохідність дорівнює 20 %, а дійсна очікувана дохідність = 18 %. (Відповідь: -2) Портфель складається з двох активів. Питома вага першого активу 25 %, другого = 75 %, альфа портфеля = 5, першого активу = 3. Визначте альфу другого активу. (Відповідь: 5, 67)

Оцінювання ефективності управління портфелем не можна здійснювати ізольовано (абсолютно), без порівняння з іншими реальними портфелями або ринковим (індексним) портфелем. Джек Трейнор уперше запропонував коефіцієнт, який врахував одночасно дохідність і ризик. За еталон для оцінювання ефективності конкретного портфеля цінних паперів використано показник надлишкової дохідності ринкового портфеля, розрахований на підставі реального фондового індексу і віднесений до рівня ринкового ризику. Критерій Трейнора обчислюють за певний період часу, він являє собою відношення надлишкової дохідності (премії за ризик) портфеля до показника (міри) системного ризику . Для і-го портфеля цінних паперів він становить (Ті): де Rі — середньорічна дохідність і-го портфеля за певний період; Rо — середньорічна безризикова ставка доходу за цей же період; і — історичний -коефіцієнт і-го портфеля за цей період.

Для ринкового портфеля критерій Трейнора (Тт) становить: де: Rm — середньорічна ринкова дохідність за певний період; Rо — середньорічна безризикова ставка доходу; m — міра системного ризику ринкового портфеля ( m ринку = 1, 0).

Вище значення критерію Ті свідчить про досконаліший склад портфеля інвестора, незалежно від його ставлення до ризику. Критерій Трейнора дає змогу зіставляти різні портфелі на підставі відносного показника надлишкового доходу за портфелем на одиницю вимірювання системного ризику. Припустімо, що за останні п років середньорічна дохідність сукупного ринкового (індексного) портфеля становила 16 %, тобто Rm = 16, а безризикова дохідність Rо = 8 %. За портфелем цінних паперів фірми A середня дохідність за той самий проміжок часу становила 17 %, фірми B = 0, 32 %, фірми C =14 %, показники системного ризику відповідно 1 = 0, 89, 2 = 1, 08 і 3 = 1, 2. На підставі цієї інформації можна обчислити критерій Трейнора для ринкового портфеля (Тm) і кожного (і-го) портфеля зазначених фірм: Найвище значення критерію Трейнора Т 2 притаманне портфелю цінних паперів фірми B. Цей портфель забезпечив найвищу дохідність на одиницю ризику й згідно з розрахунками може вважатися найефективнішим.

У. Шарп запропонував інший критерій (коефіцієнт), подібний до критерію Трейнора, але який враховує загальний ризик портфеля, визначений як стандартне відхилення σ, а не тільки системний -ризик. У загальному вигляді для і-го портфеля критерій Шарпа (S) за певний період визначають так: де: Rі — середньорічна дохідність і-го портфеля за певний період; Rо — безризикова дохідність; σі — історичне значення стандартного відхилення і-го портфеля. Числівник цього рівняння визначає надлишкову дохідність (премію за ризик), знаменник — загальний ризик, тобто критерій Шарпа визначає премію за ризик на одиницю вимірювання загального ризику. Коефіцієнт Шарпа характеризує для портфеля міру стабільності (стійкості) перевищення безризикової дохідності (надлишкової дохідності).

Припустімо, що середньорічна дохідність ринку Rm упродовж n років дорівнює 16 %, а безризикова дохідність Rо = 8 %. Стандартне відхилення як показник ризику σ приблизно 21, 2 залишається незмінним на ринку акцій упродовж багатьох років, тому саме це значення найчастіше використовують у різних обчисленнях у разі поточного оцінювання і на майбутнє. Додатково розглядаються дані стосовно портфелів цінних паперів фірм E, L і K, які мали в аналізованому періоді середньорічну дохідність відповідно 17, 32 і 13 % і стандартне відхилення як міру ризику відповідно 0, 13, 0, 19 і 0, 13. На підставі наведених даних обчислюємо коефіцієнт Шарпа: для ринку для портфелів цінних паперів зазначених фірм: Аналізуючи ці дані, можна дійти висновку, що найефективніший портфель у фірми «І» . Найнижчий рівень премії за ризик на одиницю вимірювання ризику має портфель фірми «К» . Проте всі розглянуті портфелі ефективніші за ринок.