Модель обслуживания машинного парка_Баталов.pptx
- Количество слайдов: 24

МОДЕЛЬ ОБСЛУЖИВАНИЯ МАШИННОГО ПАРКА

Модель обслуживания машинного парка представляет собой модель замкнутой системы массового обслуживания.

Система массового обслуживания(СМО) это система, которая производит обслуживание поступающих в неё требований. Обслуживание требований в СМО производится обслуживающими приборами.

Модель обслуживания машинного парка Например, обслуживается машинный парк, состоящий из N машин, бригадой R механиков (N > R), причем каждая машина может обслуживаться только одним механиком. Здесь машины являются источниками требований (заявок на обслуживание), а механики обслуживающими каналами.

Неисправная машина после обслуживания используется по своему прямому назначению и становится потенциальным источником возникновения требований на обслуживание.

Рассмотрим все на примере: Пусть для обслуживания десяти персональных компьютеров (ПК) выделено два инженера одинаковой производительности. Поток отказов (неисправностей) одного компьютера – пуассоновский(поток однородных событий) с интенсивностью l = 0, 2. Время обслуживания ПК подчиняется показательному закону. Среднее время обслуживания одного ПК одним инженером составляет: t=1, 25 час.

Возможны следующие варианты организации обслуживания ПК: • оба инженера обслуживают все десять компьютеров, так что при отказе ПК его обслуживает один из свободных инженеров, в этом случае R= 2, N= 10; • каждый из двух инженеров обслуживает по пять закрепленных за ним ПК. В этом случае R= 1, N= 5. Необходимо выбрать наилучший вариант организации обслуживания ПК.

Решение 1. Вычислим параметр обслуживания: 2. Приведенная интенсивность: 3. Вычислим вероятностные характеристики СМО для двух вариантов организации обслуживания ПК.

Вариант 1 Определим вероятности состояний системы:



Учитывая, что и используя результаты расчета Рк, вычислим Р 0: Откуда PQ = 0, 065, тогда

Определим среднее число компьютеров в очереди на обслу живание:

Определим среднее число ПК, находящихся в системе (на об служивании и в очереди):

Определим среднее число инженеров, простаивающих из за от сутствия работы: Коэффициент простоя персонального компьютера в очереди следующий:

Коэффициент использования компьютеров определяется по формуле Коэффициент простоя обслуживающих инженеров рассчитывая так:

Среднее время ожидания ПК обслуживания

Вариант 2 Определим вероятности состояний системы:

Откуда тогда Среднее число компьютеров в очереди на обслуживание таково:

Среднее число компьютеров, находящихся на обслуживании и в очереди, рассчитывается так: Среднее число инженеров, простаивающих из за отсутствия работы:

Коэффициент простоя персонального компьютера в очереди: Коэффициент использования компьютеров: Среднее время ожидания ПК обслуживания:
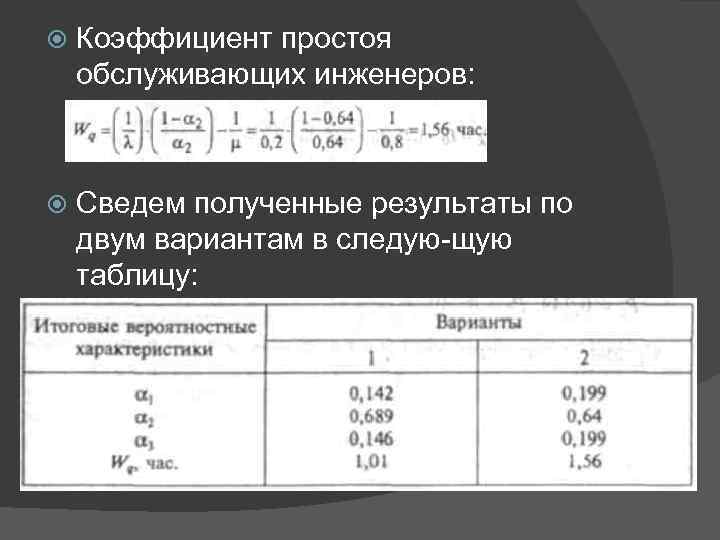
Коэффициент простоя обслуживающих инженеров: Сведем полученные результаты по двум вариантам в следую щую таблицу:

Таким образом, в варианте 1 каждый компьютер стоит в очере ди в ожидании начала его обслуживания приблизительно 0, 142 ча сти рабочего времени, что меньше этого показателя при варианте 2 организации работ. Далее в варианте 1 вероятность того, что ПК в любой момент времени будет работать выше, чем в варианте 2, и равна а 12 0, 689 > а 22 =0, 64. Очевидно, вариант I организации работ по обслуживанию ПК эффективнее, чем вариант 2.

Конец.
Модель обслуживания машинного парка_Баталов.pptx