Model Independent Visual Servoing CMPUT 610 Literature Reading

Model Independent Visual Servoing CMPUT 610 Literature Reading Presentation Zhen Deng

Introduction Summaries and Comparisons of Traditional Visual Servoing and Model independent Visual Servoing emphasizing on the latter. w Works are mostly from Jenelle A. Piepmeier’s thesis and Alexandra Hauck’s thesis w

Visual Servo w Visual servo control has the potential to provide a low-cost, low-maintenance automation solution for unstructured industries and environments. w Robotics has thrived in ordered domains, it has found challenges in environments that are not well defined.

Traditional Visual Servoing w Precise knowledge of the robot kinematics, the camera model, or the geometric relationship between the camera and the robot systems is assumed. w Need to know the exact position of the endeffector and the target in the Cartesian Space. w Require lots of calculation.

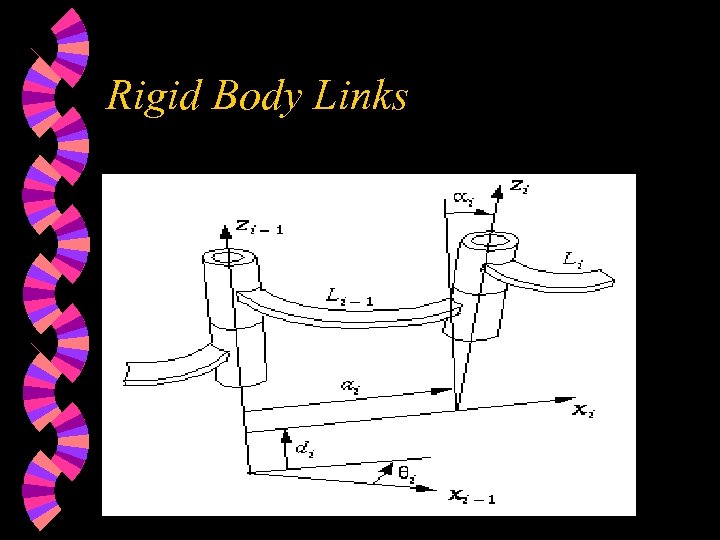Rigid Body Links

Forward Kinematics The Denavit-Hartenberg Notation: . Transz(d). Rotx(a). Trans(a) i-1 T i = Rotz(q) w Transformation 0 0 1 2 n-1 n T e= T 1 T 2 T 3 … T n T e w

Jacobian by Differential Velocity variables can transformed between joint space and Euclidean space using Jacobian matrices w Dx = J * Dq w Dq = J Dx w Jij = ¶qi/ ¶xj w

Calibrated Camera Model

Model Independent Visual Servoing An image-based Visual Servoing method. w Could be further classified as dynamic lookand-move according to the classification scheme developed by Sanderson and Weiss. w Estimate the Jacobian on-line and does not require calibrated models of either of the camera configuration or the robot kinematics. w

History Martin Jagersand formulates the visual Servoing problem as a nonlinear least squares problem solved by a quasi-Newton method using Broyden Jacobian estimation. w Base on Martin’s work, Jenelle P adds a frame to solve the problem of grasping a moving target. w me ? … w

Reaching a Stationary Target w w w Residual error f(q) = y(q) - y*. Goal: minimize f(q) Df = fk - fk-1 Jk = Jk-1 + (Df-Jk-1 Dq) Dq. T/ Dq. TDq qk+1 = qk -J-1 kfk

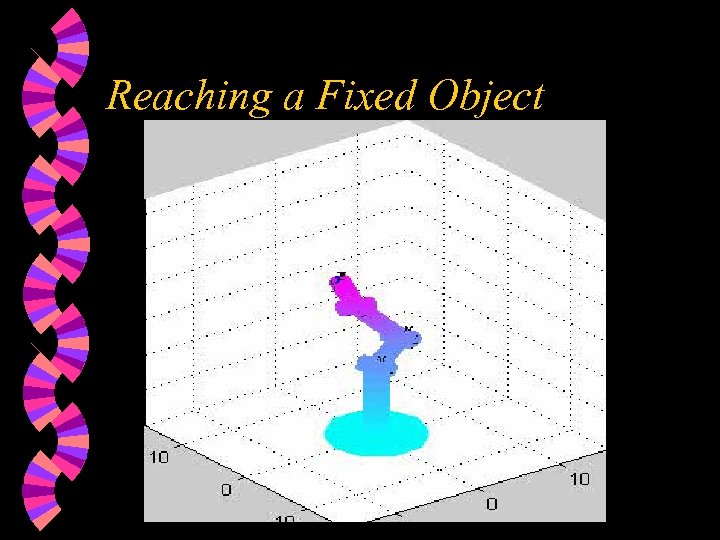Reaching a Fixed Object

Tracking the moving object Interaction with a moving object, e. g. catching or hitting it, is perhaps the most difficult task for a hand-eye system. w Most successful systems presented in paper uses precisely calibrated, stationary stereo camera systems and image-processing hardware together with a simplified visual environment. w

Peter K. Allen’s Work Allen et al. Developed a system that could grasp a toy train moving in a plain. The train’s position is estimated from(hardwaresupported) measurements of optic flow with a stationary, calibrated stereo system. w Using a non-linear filtering and prediction, the robot tracks the train and finally grasps it. w

“Ball player” Andersson’s ping-pong player is one of the earliest “ball playing” robot. w Nakai et al developed a robotic volleyball player. w

Jenelle’s modification to Broyden w w w Residual error f(q, t) = y(q) - y*(t). Goal: minimize f(q, t) Df = fk - fk-1 Jk = Jk-1 + (Df - Jk-1 Dq + (¶ y*(t)/ ¶t *Dt) ) Dq. T/ Dq. TDq qk+1 = qk -(Jk. TJk)-1 Jk. T (fk - (¶ y*(t)/ ¶t *Dt) ).

Convergence The residual error converges as the iterations increasing. w While the static method does not. w The mathematics proof of this result could be found in Jenelle’s paper. w

Experiments with 1 DOF system

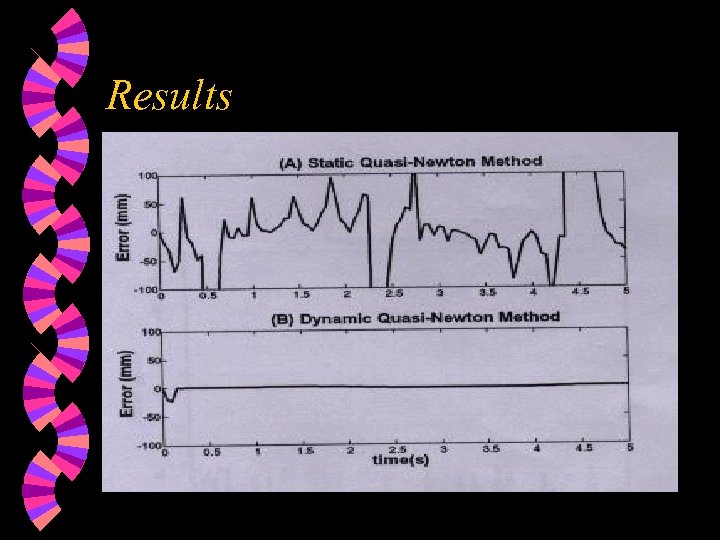Results

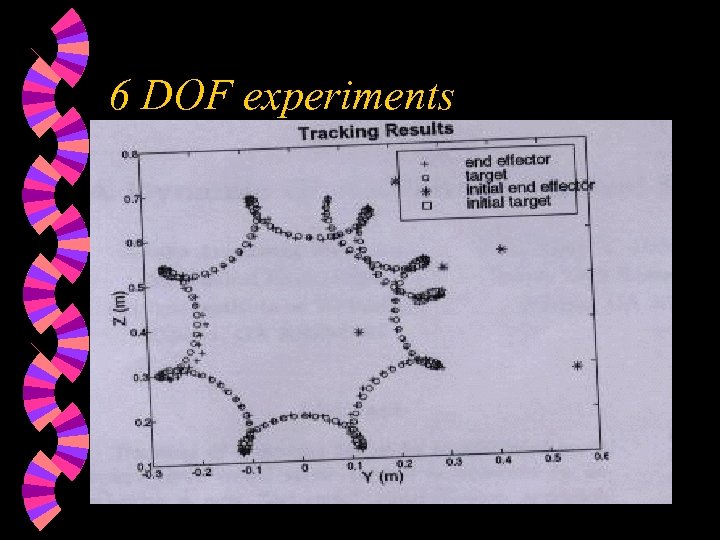6 DOF experiments

Future work ? Analysis between the two distinct ways of computing the Jacobian Matrix. w Solving the tracking problem without the knowledge of target motion. w More robust … ? w

Literature Links http: //mime 1. gtri. gatech. edu/imb/projects/m ivs/vsweb 2. html w A Dynamic Quasi-Newton Method for Uncalibrated Visual Servoing by Jenelle al w Automated Tracking and Grasping of a Moving Object with a Robotic Hand-Eye System. By Peter K. Allen w

Summary w Model Independent approach is proved to be more robust and more efficient.