Лекция_Портфель+ценных+бумаг.pptx
- Количество слайдов: 29

Модель ценных бумаг

Ценная бумага. Виды ценных бумаг n n ЦБ - финансовый инструмент, выпускаемый компаниями, финансовыми и государственными организациями, представляющий собой денежный документ - свидетельство об участии в капитале или предоставлении займа и праве на получение дохода от эмитента ценой бумаги. Виды ценных бумаг: Акция Банковская сберегательная книжка на предъявителя Вексель Депозитный сертификат Двойное складское свидетельство Закладная Инвестиционный пай Ипотечный сертификат участия Коносамент Облигация Опцион эмитента Простое складское свидетельство Приватизационные ценные бумаги Российская депозитарная расписка Сберегательный сертификат Чек

Портфель ценных бумаг n это совокупность ценных бумаг, которая принадлежит одному физическому или юридическому лицу и выступает целостным объектом управления. n Главная цель формирования портфеля ценных бумаг состоит в достижении наиболее оптимальной комбинации риска и дохода инвестора.
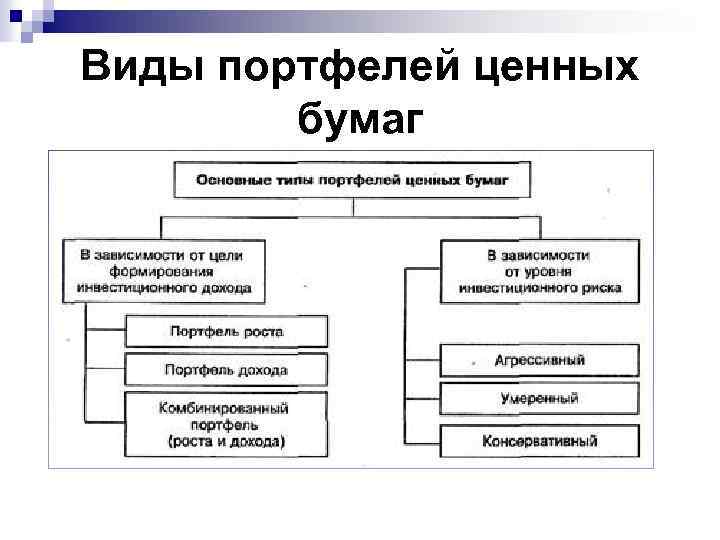
Виды портфелей ценных бумаг

Виды портфелей ценных бумаг n Портфель роста формируется из акций компаний, курсовая стоимость которых растет. Цель портфеля - рост капитальной стоимости вместе с получением дивидендов. Различают несколько видов портфелей роста. ¨ Портфель агрессивного роста нацелен на максимальный прирост капитала. Сюда входят акции молодых быстрорастущих компаний. Инвестиции в акции довольно рискованны, но могут принести самый высокий доход. ¨ Портфель консервативного роста наименее рискованный, состоит из акций крупных компаний. Состав портфеля устойчив в течение длительного времени, нацелен на сохранение капитала. ¨ Портфель среднего роста сочетает инвестиционные свойства портфелей агрессивного и консервативного роста. Наряду с надежными ценными бумагами сюда включаются рискованные фондовые инструменты. При этом гарантируются средний прирост капитала и умеренная степень риска вложений. Это наиболее популярный портфель среди инвесторов, не склонных к большому риску.

Виды портфелей ценных бумаг n n Портфель дохода ориентирован на получение высокого текущего дохода - процентных и дивидендных выплат. Здесь также различают несколько типов портфелей: ¨ портфель регулярного дохода - формируется из высоконадежных ценных бумаг и приносит средний доход при минимальном риске; ¨ портфель доходных бумаг - состоит из высокодоходных облигаций корпораций, ценных бумаг, приносящих высокий доход при среднем уровне риска. Портфели роста и дохода формируются во избежание потерь на фондовом рынке как от падения курсовой стоимости, так и от снижения дивидендных выплат.

Таким образом, становится ясно, что необходимо построить математическую модель, позволяющую в «портфельных» терминах: риск и доходность формализовать управление ценными бумагами с целью формирования портфеля ценных бумаг и управления его доходностью.

Что же такое доходность ценной бумаги в момент времени t? n n Сt- стоимость ценной бумаги в момент времени t Сt+1 - стоимость ценной бумаги в момент времени t+1 Rt – доходность ценной бумаги в момент времени t По своей природе величина Rt является случайной величиной, то есть ее значение наперед не задано.

Что же такое риск ценной бумаги в момент времени t? n n n Под риском понимается возможность не получения ожидаемого дохода или утраты (полной или частичной) средств, размещенных в данную ценную бумагу. Риск принято разделять на рыночный – единый для всех ценных бумаг, которого невозможно избежать, и индивидуальный – присущий конкретной ценной бумаге. По своей природе величина риска является случайной величиной, то есть ее значение наперед не задано. Есть ли формула оценивающая риск конкретной ценной бумаги? Возможна ли такая формула? Принцип построения такой формулы один: риск должен минимальным, а при этом доходность максимальна. Это «идеальная модель» ценной бумаги. Некий предел ее положения!
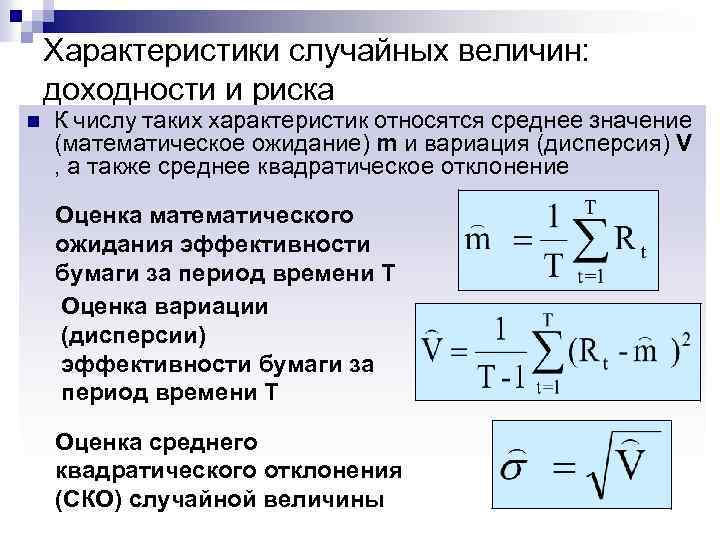
Характеристики случайных величин: доходности и риска n К числу таких характеристик относятся среднее значение (математическое ожидание) m и вариация (дисперсия) V , а также среднее квадратическое отклонение Оценка математического ожидания эффективности бумаги за период времени Т Оценка вариации (дисперсии) эффективности бумаги за период времени Т Оценка среднего квадратического отклонения (СКО) случайной величины

Статистические оценки параметров доходности и риска ценных бумаг Определяет среднее значение доходности Rt. Определяет отклонение доходности от среднего значения. Если , то отклонения нет и Rj точно предсказуемая, то есть неслучайная величина. Чем больше вариация, тем больше неопределенность в предсказании эффективности ценной бумаги и, как следствие, тем больший риск инвестора при ее приобретении. Поэтому величина вариации или СКО считается мерой риска.
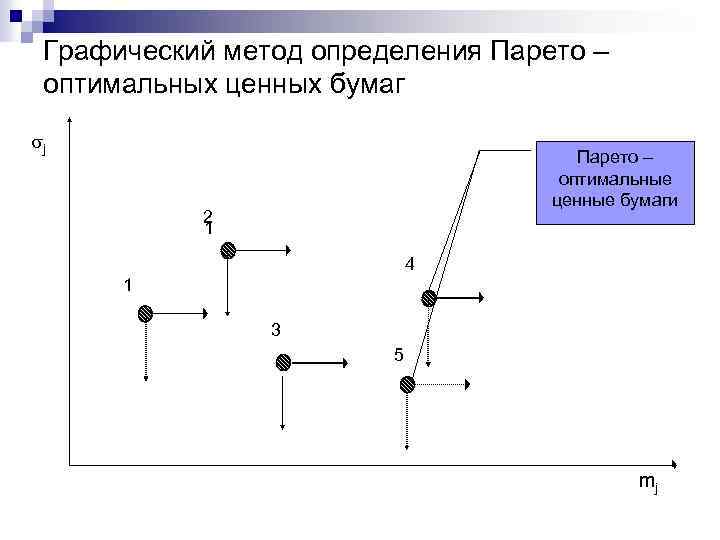
Графический метод определения Парето – оптимальных ценных бумаг j Парето – оптимальные ценные бумаги 2 1 4 1 3 5 mj

n Мы рассмотрели простой графический прием, который позволяет из множества точек (ценных бумаг) выделить те, которым есть более предпочтительные. n Для этого следует построить в каждой точке как в начале координат положительный квадрант с направлением оси ординат сверху вниз. n Если в этом квадранте расположена хотя бы одна точка, то точке в начале координат есть предпочтительная, т. е. точка в начале координат квадранта обладает худшими характеристиками, чем те, которые попали внутрь квадранта. n Исключив из рассмотрения такие точки, которым есть предпочтительные, получим множество точек, которые называются оптимальными по Парето (Парето-оптимальными) (в нашем примере это точки 4 и 5).

n Строгими математическими методами принципиально возможно выделить оптимальные по Парето точки (ценные бумаги). n Однако выбрать наилучшую (наиболее предпочтительную из Парето -оптимальных) с использованием дополнительных неформальных процедур (например, с помощью экспертных оценок специалистов).

Портфель ценных бумаг. Модели оптимизации

Портфель ценных бумаг Формализуем наши представления о портфеле ценных бумаг. Пусть в некоторый портфель P входи n ценных бумаг для каждой из которых определены как минимум 2 параметра: R – доходность и - риск Таким образом, для каждой j –ой бумаги определена пара (Rj и ) Это позволяет нам ввести понятие доходности и риска портфеля, как некоторой интегральной характеристики портфеля, то есть ввести понятия: риск и доходность портфеля (Rp )

n n Доходность портфеля Rp аналогично доходностью ценной бумаги Rj является точно непредсказуемой, то есть случайной величиной. Для ее характеристики используются оценки , которые могут быть вычислены по прошлым значениям (статистике) Rpt для t=1, 2, …T. Оценка математического ожидания эффективности портфеля ценных бумаг Оценка вариации (риска ) портфеля ценных бумаг Разберемся теперь с понятием риска портфеля ценных бумаг. Как его вычислить? Какие «подводные» камни здесь имеются?

Правила формирования портфеля ценных бумаг Величина риска портфеля отличается от величины риска ценной бумаги. Это объясняется просто: существуют ценные бумаги на рынке изменение цены на которые автоматически повлечет изменения цены на связанные с ними бумаги. В этом случае говорят о корреляции ценных бумаг n Доходность ценных бумаг и портфеля ценных бумаг величины случайные. n Портфель ценных бумаг формируется из Паретооптимальных ценных бумаг. n Доходность портфеля ценных бумаг определяется доходностью каждой бумаги и долей этой бумаги в портфеле. Портфель может включать: ¨ некоррелированные бумаги, рекомендуется диверсификация (разнообразие ценных бумаг) портфеля. ¨ коррелированные бумаги , диверсификация неэффективна

Параметром связи доходности ценных бумаг принято считать оценку ковариации случайных величин При наличии аналогичной статистики для случайной величины Rit , оценка ковариации случайных величин Rit и Rjt определяется выражением

Построим модель n Пусть инвестор располагает денежной суммой S и расходует ее на приобретение n видов ценных бумаг. Будем полагать, что на приобретение j бумаги он выделяет sj денежных единиц так, что n Поскольку на единицу затрат на приобретение бумаги j доход равен Rj , то ожидаемый доход от приобретения ценных бумаг вида j составит sj. Rj, а ожидаемый доход от приобретения n ценных бумаг равен.

Совокупность n ценных бумаг, приобретенная инвестором, называется портфелем ценных бумаг. Эффективность портфеля Rp по аналогии с эффективностью ценной бумаги определяется как отношение ожидаемого дохода инвестора к его затратам, то есть - доля затрат инвестора на приобретение ценных бумаг вида j.

Изучим некоторые важнейшие (для инвестора) свойства портфеля ценных бумаг. n Пусть портфель состоит из ценных бумаг, эффективности Rj , для которых взаимно некоррелированы, то есть n Некоррелированность двух ценных бумаг i и j имеет место в тех случаях, когда изменение эффективности одной из них не влечет за собой изменение эффективности другой (например, курс(эффективность) акций компаний по переработке сельскохозяйственного сырья мало влияет на курс акций (эффективность) ювелирных компаний). n Количественно коррелированность двух видов ценных бумаг i и j непосредственно может быть установлена расчетом оценок ковариаций

Итак окончательно имеем: Получим оценку математического ожидания портфеля (сумма произведений МО эффективности каждой бумаги, входящей в портфель, на её долю). Получим оценку риска портфеля, как оценку коэффициента вариации (или СКО) с учетом долей каждой из бумаг в портфеле

n n n Оценим количество бумаг в портфеле. Пусть хmax- максимальная доля в портфеле ценных бумаг какой-то конкретной бумаги, то есть хj <=хmax. максимально рискованная бумага Тогда риск портфеля n Если считать, что То для портфеля Т. е. риск портфеля меньше риска бумаги, имеющей максимальный риск. Количество бумаг в портфеле от 8 до 20

n Таким образом, следует, что с ростом n - количества видов ценных бумаг, включенных в портфель, при неизменности ожидаемой эффективности сокращается риск портфеля и при. n Полученный вывод является частным случаем закона больших чисел в теории вероятностей, а в теории финансового рынка называется эффектом диверсификации (разнообразия) портфеля ценных бумаг. n Именно этим правилом руководствуются различные инвестиционные фонды, которые деньги вкладчиков (инвесторов) помещают в наборы по возможности независимых акций, сокращая тем самым риск своих инвесторов.

Пример n Рассматриваются два вида ценных бумаг j =1 и j =2 и m 1=12; 1= 4; m 2 =8; 2 = 3. Тогда в соответствии с ранее приведёнными формулами следует. Таким образом, даже при n = 2 и неравных m риск портфеля становится меньше минимального из рисков ценных бумаг (2, 5 < 3), а ожидаемая эффективность портфеля равна средней эффективности составляющих ценных бумаг.

n Если , то Таким образом при полной корреляции эффективностей ценных бумаг эффект диверсификации портфеля не имеет места, так как согласно неравенству СКО не уменьшается с ростом n , а остается не меньше минимального из рисков.

Формирование портфеля ценных бумаг

Правила формирования портфеля ценных бумаг Структура портфеля акций: треть – крупные компании, треть – средние компании, треть – небольшие компании. Номенклатура портфеля акций: портфель должен состоять акции не менее 12 компаний. Капитал необходимо распределять между различными сферами деятельности (источниками прибыли). «Правило пяти пальцев» : одна акция из пяти приносит убытки, три – достигают целей (соответствующих им ожидаемых норм прибыли), еще одна – повышенный успех. «Золотое правило инвестирования» : покупать надо дешево, а продавать – дорого.
Лекция_Портфель+ценных+бумаг.pptx