d15a3fe601aa0dd5e1a1c4239a75e345.ppt
- Количество слайдов: 26

MODEL BUILDING IN REGRESSION MODELS

Model Building and Multicollinearity • Suppose we have five factors that we feel could linearly affect y. If all 5 are included we have: y = 0 + 1 x 1 + 2 x 2 + 3 x 3 + 4 x 4 + 5 x 5 + • But while the p-value for the F-test (Significance F) might be small, one or more (if not all) of the pvalues for the individual t-tests may be large. • Question: Which factors make up the “best” model? – This is called model building

Model Building • There many approaches to model building – Elimination of some (all) of the variables with high p-values is one approach • Forward stepwise regression “builds” the model by adding one variable at a time. • Modified F-tests can be used to test if the a certain subset of the variables should be included in the model.

The Stepwise Regression Approach • y = 0 + 1 x 1 + 2 x 2 + 3 x 3 + 4 x 4 + 5 x 5 + • Step 1: Run five simple linear regressions: – – – y = 0 + 1 x 1 y = 0 + 2 x 2 y = 0 + 3 x 3 y = 0 + 4 x 4 y = 0 + 5 x 5 Suppose this model has lowest p-value (< α) • Check the p-values for each – – Note for simple linear regression Significance F = p-value for the t-test.

Stepwise Regression • Step 2: Run four 2 -variable linear regressions: Check Significance F and p-values for: – y = 0 + 4 x 4 + 1 x 1 – y = 0 + 4 x 4 + 2 x 2 – y = 0 + 4 x 4 + 3 x 3 – y = 0 + 4 x 4 + 5 x 5 Suppose lowest p-values (< α) Add X 3

Stepwise Regression • Step 3: Run three 3 -variable linear regressions: – y = 0 + 3 x 3 + 4 x 4 + 1 x 1 – y = 0 + 3 x 3 + 4 x 4 + 2 x 2 – y = 0 + 3 x 3 + 4 x 4 + 5 x 5 • Suppose none of these models have all p-values < α -- STOP -- best model is the one with x 3 and x 4 only
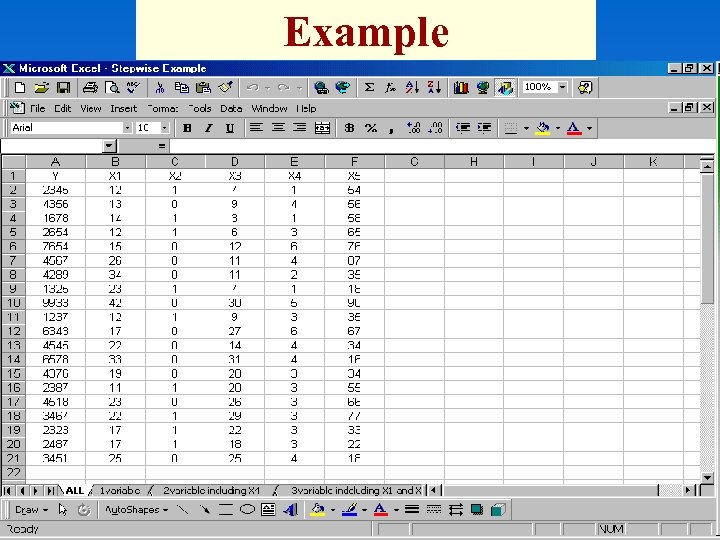
Example
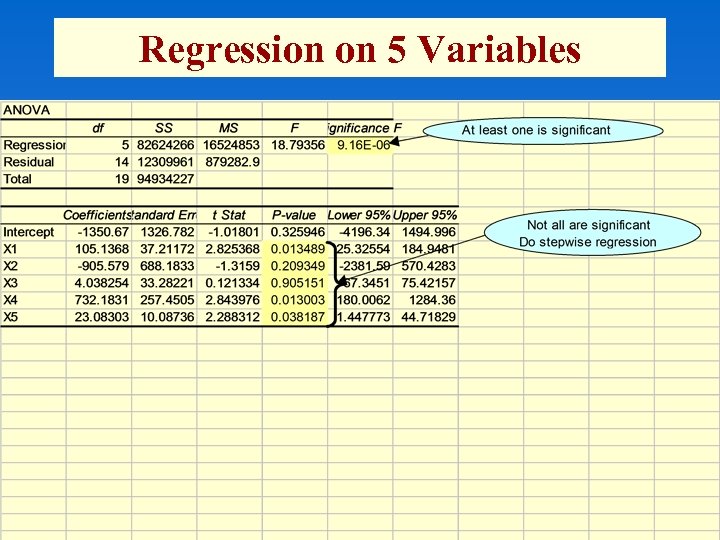
Regression on 5 Variables
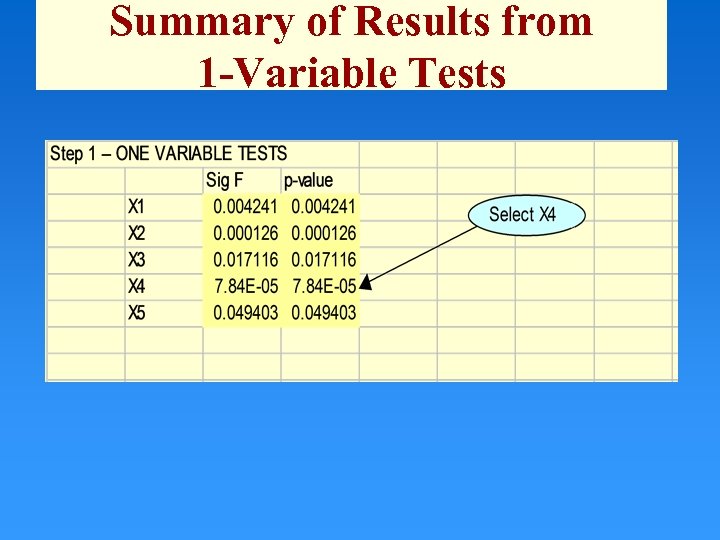
Summary of Results from 1 -Variable Tests

Performing Tests With More Than One Variable • Remember the Range for X must be contiguous • Use CUT and INSERT CUT CELLS to arrange the X columns so that they are next to each other
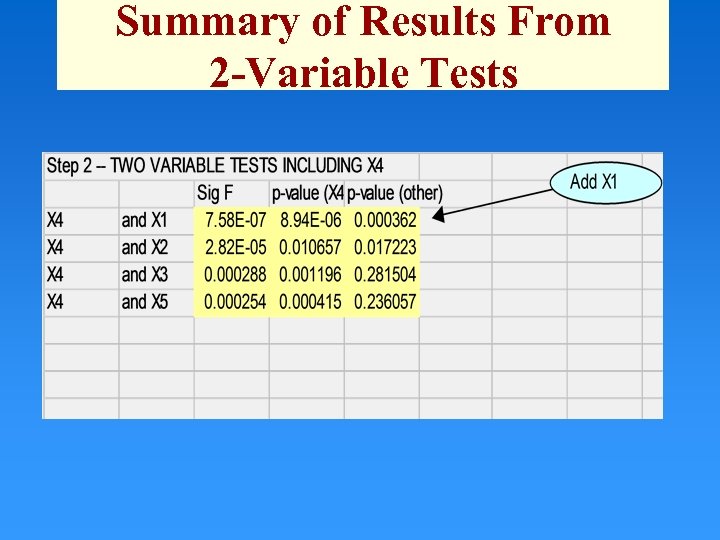
Summary of Results From 2 -Variable Tests
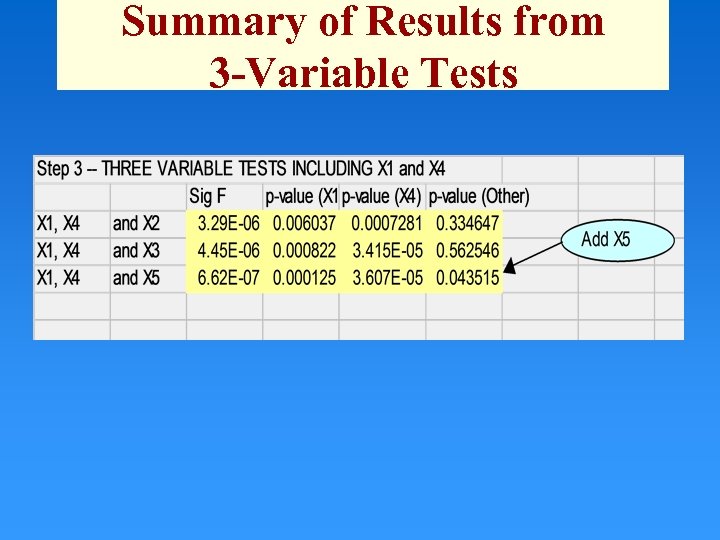
Summary of Results from 3 -Variable Tests
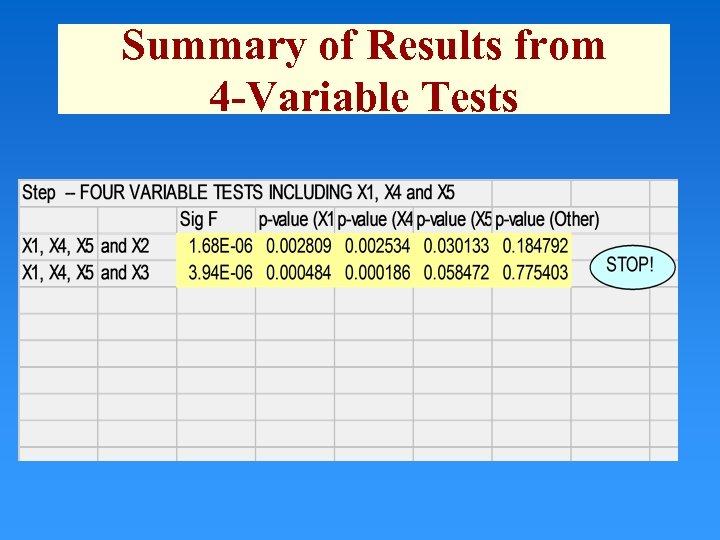
Summary of Results from 4 -Variable Tests

Best Model • The best model is the three-variable model that includes x 1, x 4, and x 5.

TESTING PARTS OF THE MODEL • Sometimes we wish to see whether to keep a set of variables “as a group” or eliminate them from the model. – Example: Model might include 3 dummy variables to account for how the independent variable is affected by a particular season (or quarter) of the year. • Will either keep all seasons or will keep none • The general approach is to assess how much “extra value” these additional variables will add to the model. – Approach is a Modified F-test

Approach: Compare Two Models – The Full Model and The Reduced Model • Suppose a model consists of p variables and we wish to consider whether or not to keep a set of p-q of those p variables in the model. • Two models – Full model – p variables – Reduced model – q variables • For notational convenience, assume the last p-q of the p variables are the ones that would be eliminated. – Sample of size n is taken

The Modified F-Test • Modified F-Test: H 0: βq+1 = βq+2 =. . … = βp = 0 HA: At least one of these p-q β’s ≠ 0 • This is an F-test of the form: Reject H 0 (Accept HA) if: F > Fα, p-q, n-p-1 # variables considered for elimination Degrees of Freedom for the Error Term of the Full Model

The Modified F-Statistic • For this model, the F-statistic is defined by:

Example • A housing price model (Full model) is proposed for homes in Laguna Hills that takes into account p = 5 factors: – House size, Lot Size, Age, Whether or not there is a pool, # Bedrooms • A reduced model that takes into account only the first of these (q = 3) was discussed earlier. • Based on a sample of n = 38 sales, can we conclude that adding these p-q = 2 additional variables (Pool, # Bedrooms) is significant?

The Modified F-Test For This Example • Modified F-Test: H 0: β 4 = β 5 = 0 HA: At least one of β 4 and β 5 ≠ 0 For α =. 05, the test is Reject H 0 (Accept HA) if: F > F. 05, 2, 32 can be generated in Excel by FINV(. 05, 2, 32) = 3. 29.
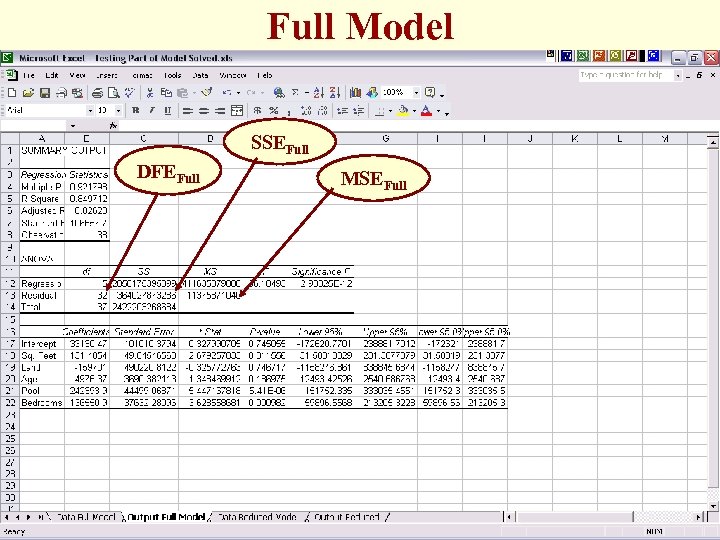
Full Model SSEFull DFEFull MSEFull
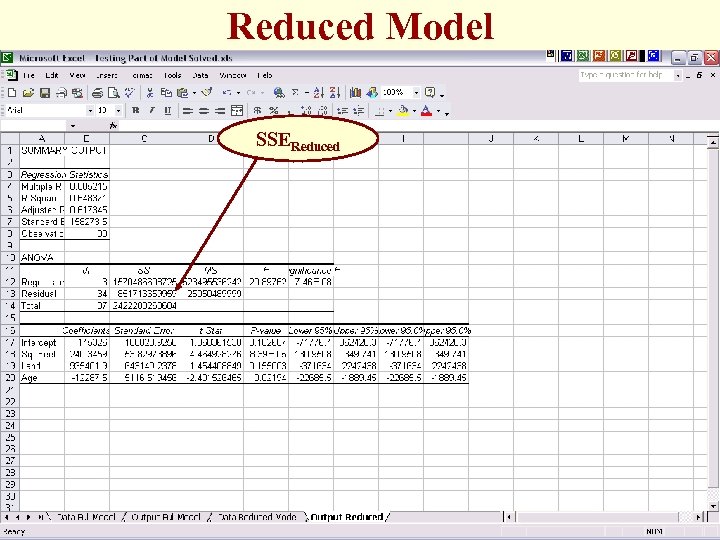
Reduced Model SSEReduced
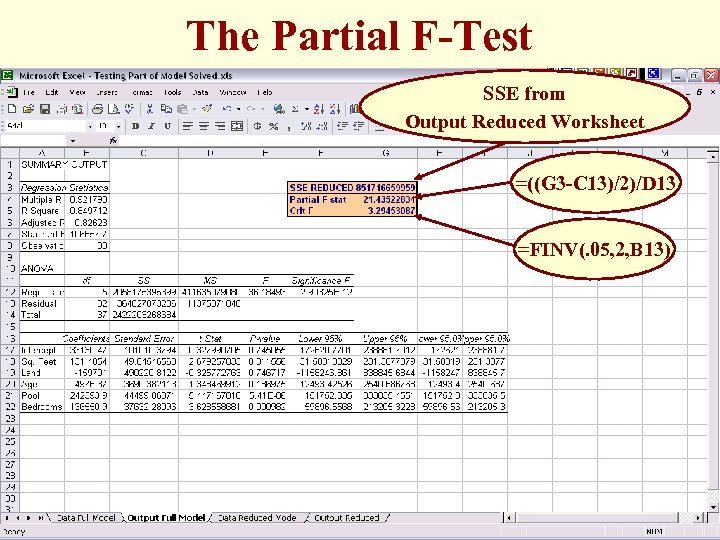
The Partial F-Test SSE from Output Reduced Worksheet =((G 3 -C 13)/2)/D 13 =FINV(. 05, 2, B 13)

The Modified F-Statistic • For this model, the modified F-statistic is: • The critical value of F = F. 05, 2, 32 = 3. 29453087 • 21. 43522834 > 3. 29453087 There is enough evidence to conclude that including Pool and Bedrooms is significant.

Review • Stepwise regression helps determine a “best model” from a series of possible independent variables (x’s) – Approach – • Step 1 – Run one variable regressions – If there is a p-value < , keep the variable with lowest p-value as a variable in the model • Step 2 – Run 2 -variable regressions – One of the two variables in each model is the one determined in Step 1 – Keep the one with the lowest p-values if both are < • Repeat with 3, 4, 5 variables, etc. until no model as has p-values < • Modified F-test for testing the significance of parts of the model – Compare F to Fα, p-q, DFE(Full), where F= ((SSEReduced – SSEFull)/(#terms removed))/MSEFull
d15a3fe601aa0dd5e1a1c4239a75e345.ppt