987436bcf3b645374601f0c59a13e2fa.ppt
- Количество слайдов: 47

Model Based Testing Property Checking for Real Jan Tretmans University of Nijmegen tretmans@cs. kun. nl © Jan Tretmans University of Nijmegen

Overview F Introduction ¨ Testing ¨ Formal methods and Testing F Formal Testing ¨ Framework ¨ Pre/post-condition program testing F Transition system testing ¨ ioco test theory ¨ a test tool ¨ an application: "Rekeningrijden" F Conclusions © Jan Tretmans University of Nijmegen 2

Overview F Introduction ¨ Testing ¨ Formal methods and Testing F Formal Testing ¨ Framework ¨ Pre/post-condition program testing F Transition system testing ¨ ioco test theory ¨ a test tool ¨ an application: "Rekeningrijden" F Conclusions © Jan Tretmans University of Nijmegen 3

Testing: to check the quality of an object by performing experiments in a controlled way w. r. t. a specification n m IUT tester n+m Software Testing : testing the quality of a software product © Jan Tretmans University of Nijmegen 4

Paradox of Software Testing is: But also: F important F much practiced F 30% - 50% of project effort F expensive F time critical F not constructive F ad-hoc, manual, error-prone F hardly theory / research F no attention in curricula F not cool : “if you’re a bad programmer you might be a tester” (but sadistic? ) sible pos s ! ents thod vem l me o mpr orma I ith f w © Jan Tretmans University of Nijmegen ? Attitude is changing: F more awareness F more professional 5
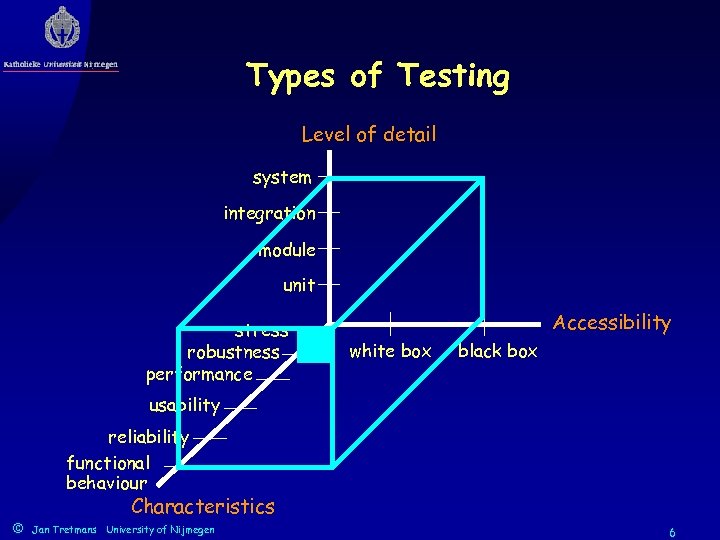
Types of Testing Level of detail system integration module unit stress robustness performance Accessibility white box black box usability reliability functional behaviour Characteristics © Jan Tretmans University of Nijmegen 6
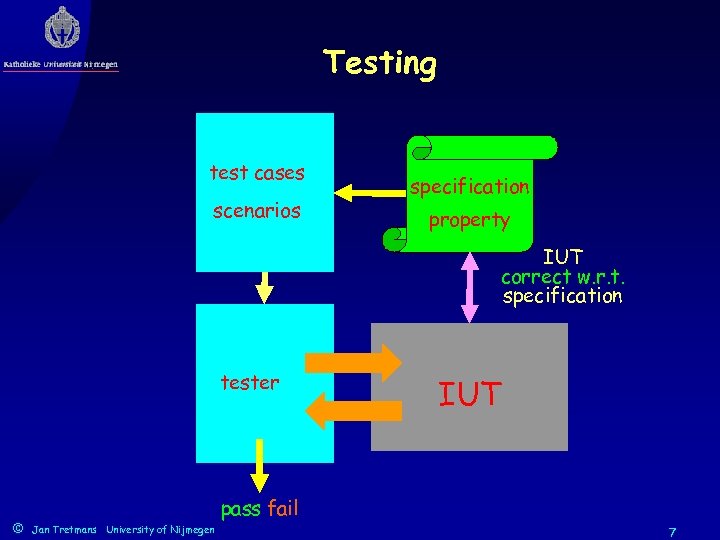
Testing test cases scenarios specification property IUT correct w. r. t. specification tester © IUT pass fail Jan Tretmans University of Nijmegen 7

Overview F Introduction ¨ Testing ¨ Formal methods and Testing F Formal Testing ¨ Framework ¨ Pre/post-condition program testing F Transition system testing ¨ ioco test theory ¨ a test tool ¨ an application: "Rekeningrijden" F Conclusions © Jan Tretmans University of Nijmegen 8

Testing & Formal Methods A Perfect Couple ? Formal methods: F proving properties F research F sound theories F “clean” Testing : F trial & error F practice F heuristics F “dirty hands” “Testing is not necessary after formal verification” “Testing can only detect the presence of errors, not their absence” “Formal methods are toys for boys” “Formal methods are only for toy problems" © Jan Tretmans University of Nijmegen 9

Formal Testing Why testing with a formal specification: F improves the testing process F precise and unambiguous basis for testing F allows automatic generation of tests Why no formal verification (theorem proving, model checking, …) : F code/structure of system not accessible (black-box) F system too complex F verification only on model of implementation F prove evidence to customer/user F no formalization possible © Jan Tretmans University of Nijmegen 10
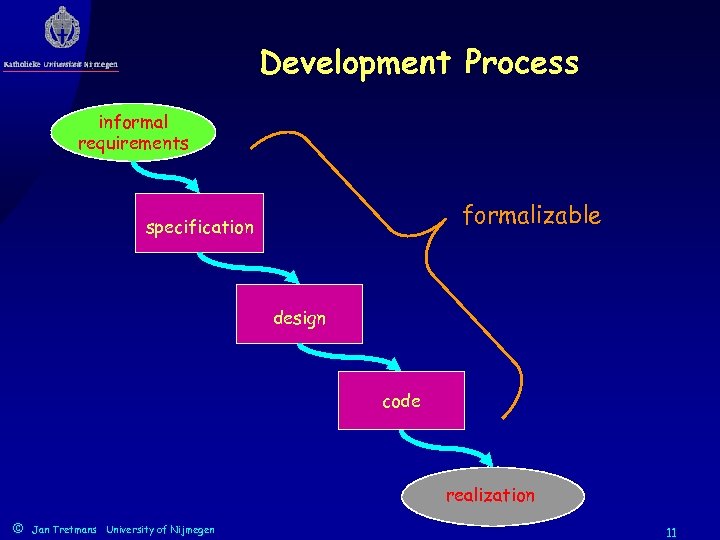
Development Process informal requirements formalizable specification design code realization © Jan Tretmans University of Nijmegen 11

Specification Based Functional Testing with Formal Methods specification s Goal: Testing functional behaviour formal testing of black-box implementation with respect to specification in formal language implementation under test based on formal definition of conformance Model assumed to be correct © Jan Tretmans University of Nijmegen 12

Overview F Introduction ¨ Testing ¨ Formal methods and Testing F Formal Testing ¨ Framework ¨ Pre/post-condition program testing F Transition system testing ¨ ioco test theory ¨ a test tool ¨ an application: "Rekeningrijden" F Conclusions © Jan Tretmans University of Nijmegen 13
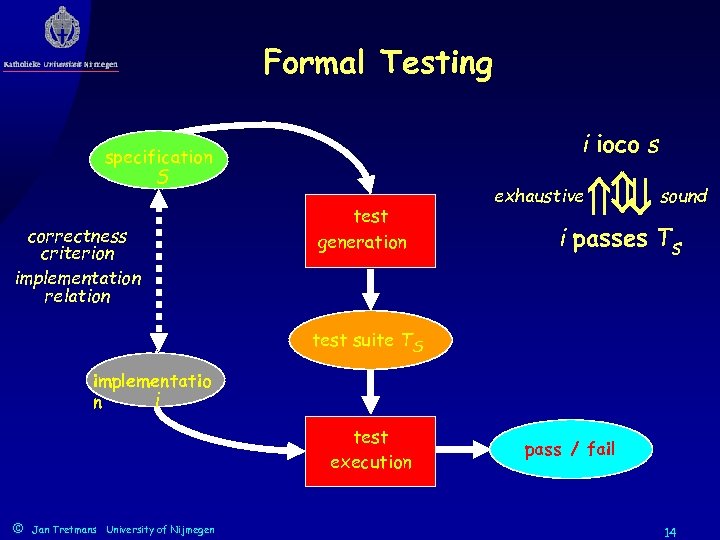
Formal Testing S correctness criterion implementation relation test generation exhaustive i ioco s specification sound i passes Ts test suite TS implementatio i n test execution © Jan Tretmans University of Nijmegen pass / fail 14

Formal Testing : Conformance specification S IUT correct wrt s correctness criterion implementatio n IUT s SPECS Specification IUT Implementation under Test IUT is concrete, physical object Model the physical world But IUT is black box ! ? Assume that model i. IUT exists © Jan Tretmans University of Nijmegen 15

Formal Testing : Test Hypothesis Test hypothesis : IUT IMPS. i. IUT MODS. t TESTS. obs ( t, IUT ) = obs ( t, i. IUT ) IUT test t © i. IUT test t Jan Tretmans University of Nijmegen 16

Formal Testing : Conformance specification S formal correctness criterion i. IUT imp s implementatio i. IUT n s SPECS Specification i. IUT MODS model of IUT Test hypothesis : each concrete IUT can be modelled by some i. IUT MODS Correctness : i. IUT imp s i. IUT is not known ; testing to learn about i. IUT © Jan Tretmans University of Nijmegen 17

Completeness of test suite Ts on models: i MODS. t Ts. obs ( t, i ) = pass exhaustive i imp s sound © Jan Tretmans University of Nijmegen 18

Testing for Conformance IUT passes Ts ? correct wrt s IUT passes Ts IUT ) t Ts. obs ( t, passes t = passobs ( t, IUT ) = pass def t Ts. obs ( t, i. IUT ) Test hypothesis : i. IUT imp s obligation : Proof t TESTS. obs ( t, IUT ) = obs ( t, i. IUT ) © t Ts. IUT passess t def IUT passes T IUT correct wrt s Jan Tretmans University of Nijmegen t Ts. IUT passes t = pass i MODS. Definition : IUT correct wrt s ( t Ts. obs ( t, i ) = pass ) i imp s 19
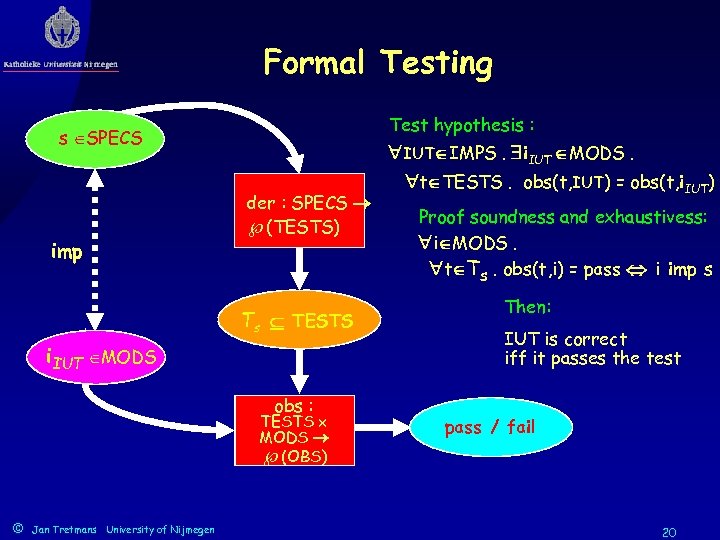
Formal Testing Test hypothesis : s SPECS imp der : SPECS (TESTS) Ts TESTS i. IUT MODS IUT IMPS obs exec : : TESTS MODS IMPS (OBS) © Jan Tretmans University of Nijmegen IUT IMPS. i. IUT MODS. t TESTS. obs(t, IUT) = obs(t, i. IUT) Proof soundness and exhaustivess: i MODS. t Ts. obs(t, i) = pass i imp s Then: IUT is correct iff it passes the test pass / fail 20

Approaches to Formal Testing Instantiations of Formal Framework F Programs as functions (pre/post-conditions) F Finite State Machine / methods with state F Labelled Transition Systems F Abstract Data Type testing © Jan Tretmans University of Nijmegen 21

Overview F Introduction ¨ Testing ¨ Formal methods and Testing F Formal Testing ¨ Framework ¨ Pre/post-condition program testing F Transition system testing ¨ ioco test theory ¨ a test tool ¨ an application: "Rekeningrijden" F Conclusions © Jan Tretmans University of Nijmegen 22

Simple Input/Output Programs x: X IUT y: Y F Specification: s X Y F Test hypothesis: implementation i : : X Y F Tests: T X F Passing a test t T : ( t, i(t) ) s F Tools: Quick. Check, G ST F Problem/challenge: select "good" subset T X: classical techniques: equivalence partitioning, boundary analysis, …… © Jan Tretmans University of Nijmegen 23

Input/Output Program: Example x: real pre: x 0 IUT i(x) = x y: real post: |y y - x| 0. 00001 F Specification: prop. Sqrt(x, y) = x 0 |y y - x| 0. 00001 F Possible test set: T = { 0, 0. 00232, 1, 1. 87392, 2738894 } F Tools like Quick. Check, G ST easily generate thousands of test cases F But still: what is a "good" set ? © Jan Tretmans University of Nijmegen 24

Overview F Introduction ¨ Testing ¨ Formal methods and Testing F Formal Testing ¨ Framework ¨ Pre/post-condition program testing F Transition system testing ¨ ioco test theory ¨ a test tool ¨ an application: "Rekeningrijden" F Conclusions © Jan Tretmans University of Nijmegen 25
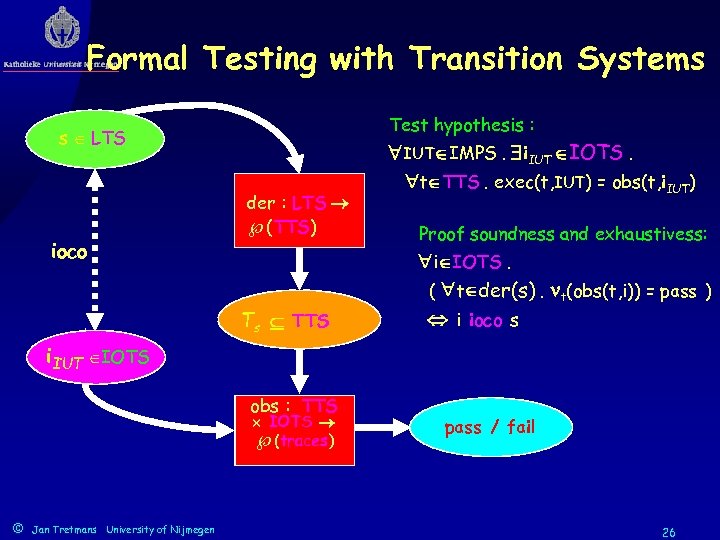
Formal Testing with Transition Systems Test hypothesis : s LTS ioco der : LTS (TTS) Ts TTS IUT IMPS. i. IUT IOTS. t TTS. exec(t, IUT) = obs(t, i. IUT) Proof soundness and exhaustivess: i IOTS. ( t der(s). t(obs(t, i)) = pass ) i ioco s i. IUT IOTS IUT IMPS obs : TTS exec : TESTS IOTS IMPS (traces) (OBS) © Jan Tretmans University of Nijmegen pass / fail 26
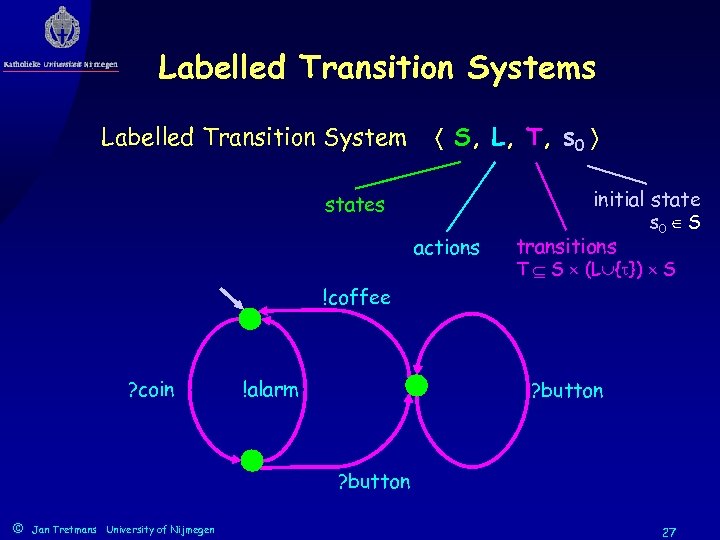
Labelled Transition Systems Labelled Transition System S, L, T, s 0 initial states actions transitions s 0 S T S (L { }) S !coffee ? coin !alarm ? button © Jan Tretmans University of Nijmegen 27

Implementation Relation ioco Correctness expressed by implementation relation ioco: i ioco s =def Straces (s) : out (i after ) out (s after ) !x LU { }. p !x Straces ( s ) = { (L { })* | s p after = { p’ | p out ( P ) = { !x LU | p !x p © p = Jan Tretmans University of Nijmegen } p’ } , p P } { | p p, p P } 28

Implementation Relation ioco Correctness expressed by implementation relation ioco: i ioco s =def Straces (s) : out (i after ) out (s after ) Intuition: i ioco-conforms to s, iff • if i produces output x after trace , then s can produce x after • if i cannot produce any output after trace , then s cannot produce any output after ( quiescence ) © Jan Tretmans University of Nijmegen 29
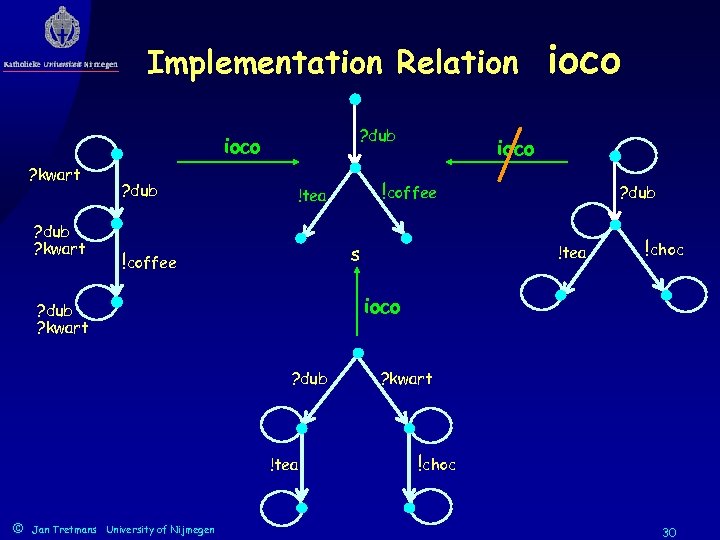
Implementation Relation ? dub ioco ? kwart ? dub !choc ioco ? dub !tea Jan Tretmans University of Nijmegen ? dub !tea s ? dub ? kwart © ioco !coffee !tea !coffee ioco ? kwart !choc 30
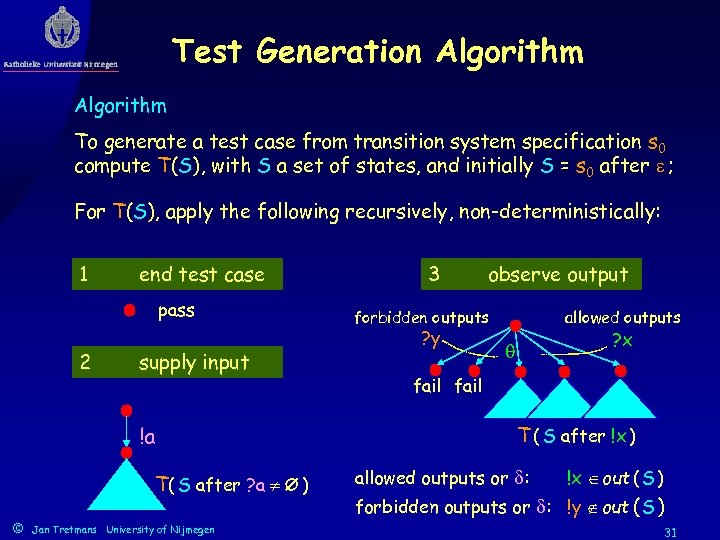
Test Generation Algorithm To generate a test case from transition system specification s 0 compute T(S), with S a set of states, and initially S = s 0 after ; For T(S), apply the following recursively, non-deterministically: 1 end test case pass 2 supply input !a T( S after ? a ) © Jan Tretmans University of Nijmegen 3 observe output forbidden outputs ? y allowed outputs ? x fail T ( S after !x ) allowed outputs or : !x out ( S ) forbidden outputs or : !y out ( S ) 31

Completeness of Test Generation For every test t generated with algorithm we have: F Soundness : t will never fail with correct implementation i ioco s implies i passes t F Exhaustiveness : each incorrect implementation can be detected with a generated test t i ioco s © Jan Tretmans University of Nijmegen implies t : i fails t 32

Overview F Introduction ¨ Testing ¨ Formal methods and Testing F Formal Testing ¨ Framework ¨ Pre/post-condition program testing F Transition system testing ¨ ioco test theory ¨ a test tool ¨ an application: "Rekeningrijden" F Conclusions © Jan Tretmans University of Nijmegen 33

A Test Tool : Tor. X F On-the-fly test generation and test execution F Implementation relation: ioco F Specification languages: LOTOS, Promela, FSP, Automata user: manual automatic next input specification check output offer input Tor. X observe output IUT pass fail inconclusive © Jan Tretmans University of Nijmegen 34
Tor. X © Jan Tretmans University of Nijmegen 35

Overview F Introduction ¨ Testing ¨ Formal methods and Testing F Formal Testing ¨ Framework ¨ Pre/post-condition program testing F Transition system testing ¨ ioco test theory ¨ a test tool ¨ an application: "Rekeningrijden" F Conclusions © Jan Tretmans University of Nijmegen 36

Tor. X Case Studies FConference Protocol academic FEasy. Link TV-VCR protocol Philips FCell Broadcast Centre component CMG F‘’Rekeningrijden’’ Payment Box protocol Interpay FV 5. 1 Access Network protocol Lucent FEasy Mail Melder CMG FFTP Client academic F“Oosterschelde” storm surge barrier-control CMG © Jan Tretmans University of Nijmegen 37

Interpay ‘’Rekeningrijden’’ Payment Box Protocol © Jan Tretmans University of Nijmegen 38

“Rekeningrijden” Characteristics : F Simple protocol F Parallellism : ¨ many cars at the same time F Encryption F Real-time issues F System passed traditional testing phase © Jan Tretmans University of Nijmegen 39
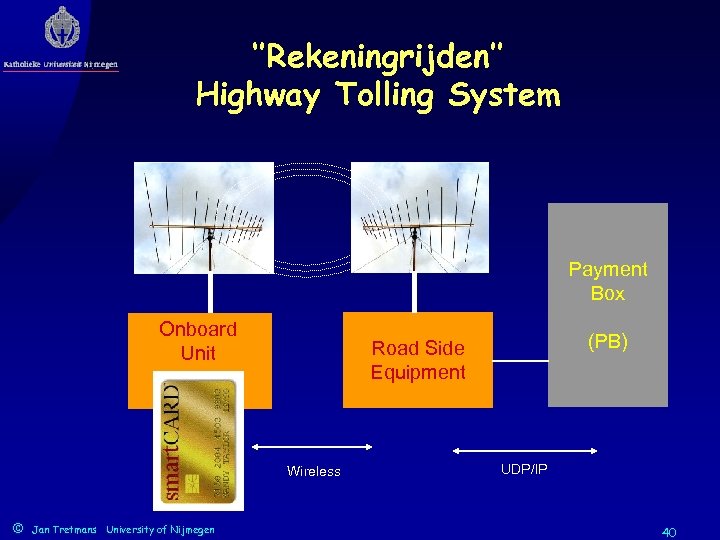
‘’Rekeningrijden’’ Highway Tolling System Payment Box Onboard Unit Wireless © Jan Tretmans University of Nijmegen (PB) Road Side Equipment UDP/IP 40
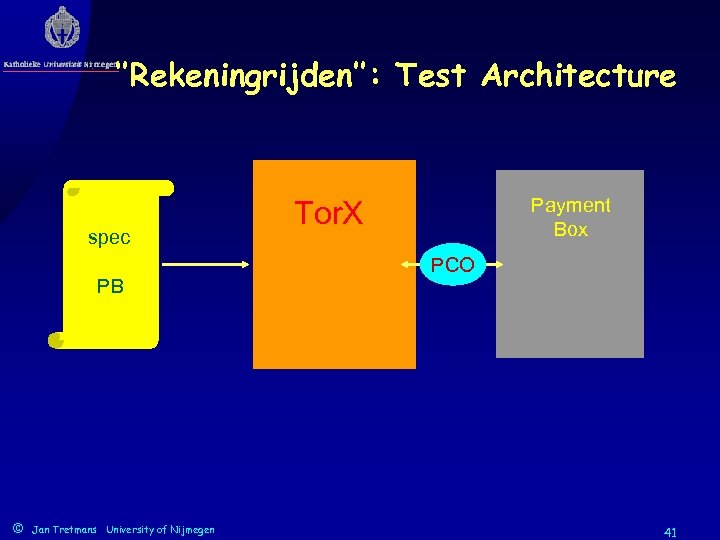
‘’Rekeningrijden’’: Test Architecture spec PB © Jan Tretmans University of Nijmegen Payment Box Tor. X PCO 41
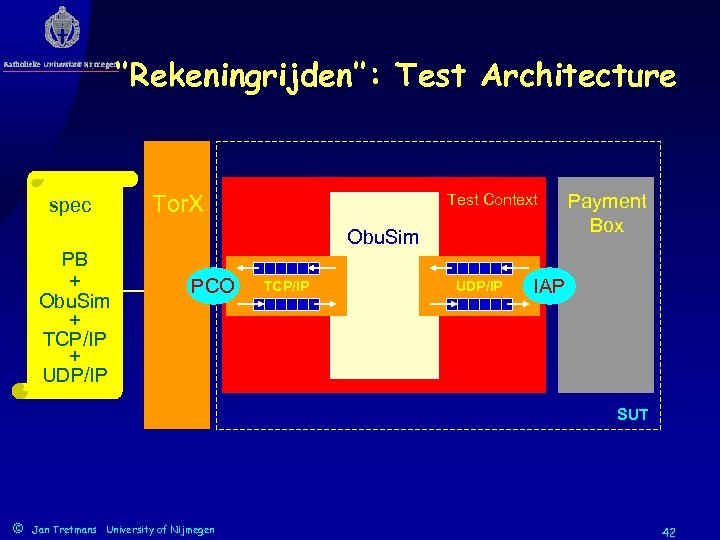
‘’Rekeningrijden’’: Test Architecture spec PB + Obu. Sim + TCP/IP + UDP/IP Test Context Tor. X Obu. Sim PCO TCP/IP UDP/IP Payment Box IAP SUT © Jan Tretmans University of Nijmegen 42

‘’Rekeningrijden’’: Issues FParallellism : ¨ very easy FEncryption : ¨ Not all events can be synthesized : Leads to reduced testing power FReal-time : ¨ How to cope with real time constraints ? ¨ Efficient computation for on-the-fly testing ? ¨ Lack of theory: quiescence vs. time-out © Jan Tretmans University of Nijmegen 43

‘’Rekeningrijden” : Results FTest results : ¨ 1 error during validation (design error) ¨ 1 error during testing (coding error) FAutomated testing : ¨ beneficial: high volume and reliability ¨ many and long tests executed ( > 50, 000 test events ) ¨ very flexible: adaptation and many configurations © Jan Tretmans University of Nijmegen 44

Overview F Introduction ¨ Testing ¨ Formal methods and Testing F Formal Testing ¨ Framework ¨ Pre/post-condition program testing F Transition system testing ¨ ioco test theory ¨ a test tool ¨ an application: "Rekeningrijden" F Conclusions © Jan Tretmans University of Nijmegen 45

Concluding …… F Testing can be formal, too (M. -C. Gaudel, TACAS'95) ¨ Testing shall be formal, too F But testing can never be complete ¨ it increases confidence in correctness F Testing can be the first step: ¨ counter-example finding before expensive formal verification F Or the last: ¨ to show that not only the model is correct but also the real system © Jan Tretmans University of Nijmegen 46

Thanks to. . . University of Twente: Ed Brinksma, Lex Heerink, Axel Belinfante, Jan Feenstra, René de Vries, Machiel van der Bijl, …… Eindhoven University of Technology: Nicolae Goga, Loe Feijs, Sjouke Mauw University of Nijmegen: Pieter Koopman Philips Research Labs Eindhoven: Lex Heerink, Ron Koymans KPN Research: Erik Kwast, Henri Dol Lucent Technologies - R&D Centre Twente: Arjan de Heer Project Pampa, IRISA, Rennes (Logica)CMG Information Technology: Peter Christian, Robert Spee, Wouter Geurts, …… Interpay B. V. : Cornel van Mastrigt, Rommert Jorritsma Ordina Utopics: Pim Kars © ……… Jan Tretmans University of Nijmegen 47
987436bcf3b645374601f0c59a13e2fa.ppt