c4b8fc18a9cf54bf73a9e042c12f7416.ppt
- Количество слайдов: 12

Model-based Programming as Estimating, Planning and Executing based on Hidden State Brian C. Williams Artificial Intelligence and Space Systems Labs Massachusetts Institute of Technology

Objective Create a hybrid estimation, monitoring, diagnosis and model learning capability for physical devices that exhibit complex discrete and continuous behaviors. DEMONSTRATION: JSC BIO-Plex Mars Entry, descent & Landing
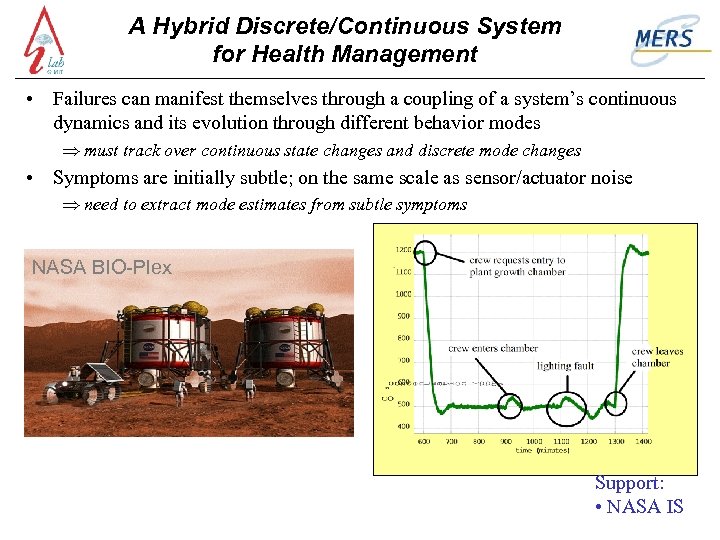
A Hybrid Discrete/Continuous System for Health Management • Failures can manifest themselves through a coupling of a system’s continuous dynamics and its evolution through different behavior modes Þ must track over continuous state changes and discrete mode changes • Symptoms are initially subtle; on the same scale as sensor/actuator noise Þ need to extract mode estimates from subtle symptoms NASA BIO-Plex Support: • NASA IS
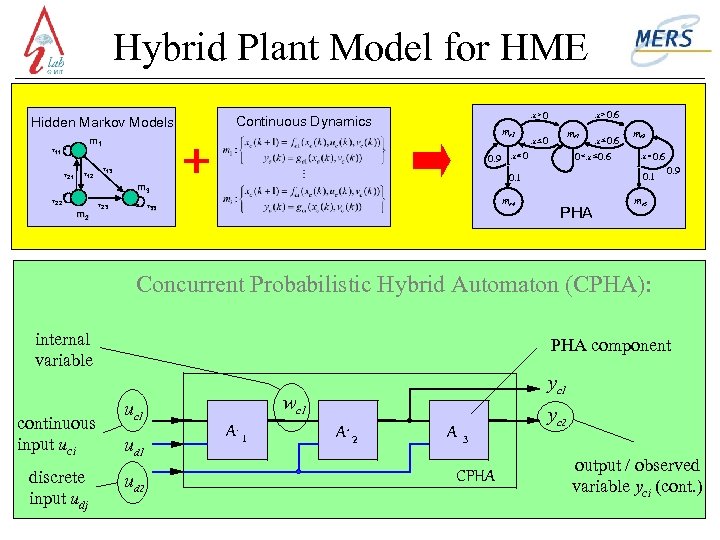
Hybrid Plant Model for HME Hidden Markov Models mr 1 m 1 t 11 t 21 t 12 0. 9 t 13 m 2 t 23 x 0 mr 2 x 0 mr 4 t 33 x 0. 6 0 x 0. 6 mr 3 x 0. 6 0. 1 m 3 t 22 x 0. 6 x 0 Continuous Dynamics PHA 0. 9 mr 5 Concurrent Probabilistic Hybrid Automaton (CPHA): internal variable continuous input uci discrete input udj PHA component wc 1 ud 2 yc 1 A 2 A yc 2 3 CPHA output / observed variable yci (cont. )
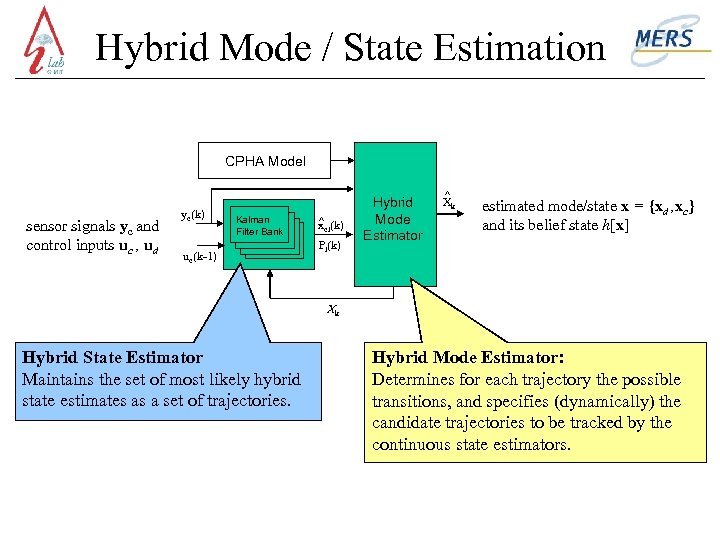
Hybrid Mode / State Estimation CPHA Model sensor signals yc and control inputs uc , ud yc(k) Kalman Filter Bank uc(k-1) ^ (k) xci Pi(k) Hybrid Mode Estimator ^ Xk estimated mode/state x = {xd , xc} and its belief state h[x] Ck Hybrid State Estimator Maintains the set of most likely hybrid state estimates as a set of trajectories. Hybrid Mode Estimator: Determines for each trajectory the possible transitions, and specifies (dynamically) the candidate trajectories to be tracked by the continuous state estimators.
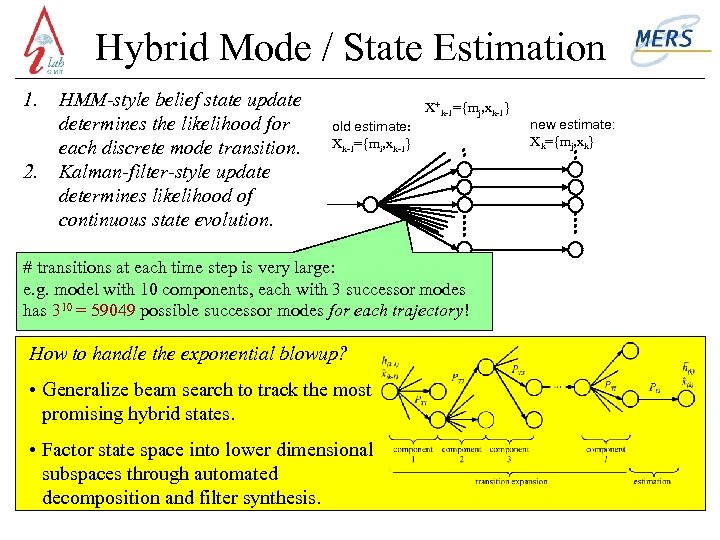
Hybrid Mode / State Estimation 1. 2. HMM-style belief state update determines the likelihood for each discrete mode transition. Kalman-filter-style update determines likelihood of continuous state evolution. X+k-1={mj, xk-1} old estimate: Xk-1={mi, xk-1} # transitions at each time step is very large: e. g. model with 10 components, each with 3 successor modes has 310 = 59049 possible successor modes for each trajectory! How to handle the exponential blowup? • Generalize beam search to track the most promising hybrid states. • Factor state space into lower dimensional subspaces through automated decomposition and filter synthesis. new estimate: Xk={mj, xk}
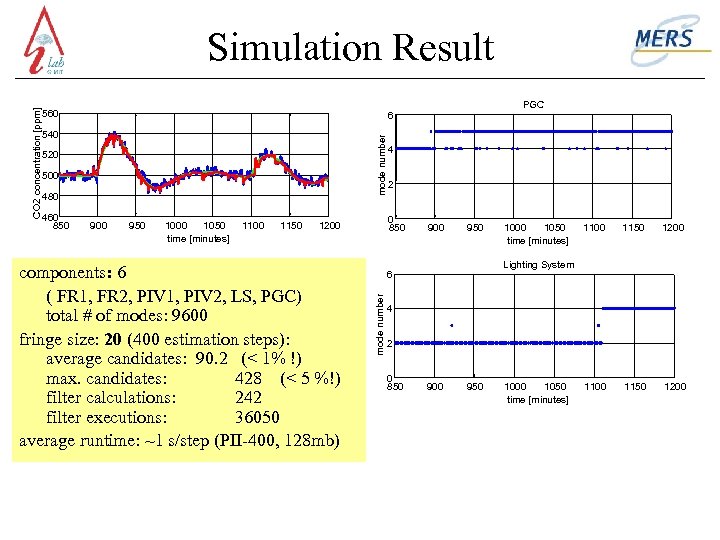
560 mode number 540 520 500 480 460 850 PGC 6 900 950 1000 1050 time [minutes] 1100 1150 components: 6 ( FR 1, FR 2, PIV 1, PIV 2, LS, PGC) total # of modes: 9600 fringe size: 20 (400 estimation steps): average candidates: 90. 2 (< 1% !) max. candidates: 428 (< 5 %!) filter calculations: 242 filter executions: 36050 average runtime: ~1 s/step (PII-400, 128 mb) 4 2 0 850 1200 950 1000 1050 time [minutes] 1100 1150 1200 Lighting System 6 mode number CO 2 concentration [ppm] Simulation Result 4 2 0 850 900 950 1000 1050 time [minutes]

Future Directions • Model-Learning as Hybrid EM • Automated Decomposition of HPCA using Dissents • Model-based Hybrid Execution
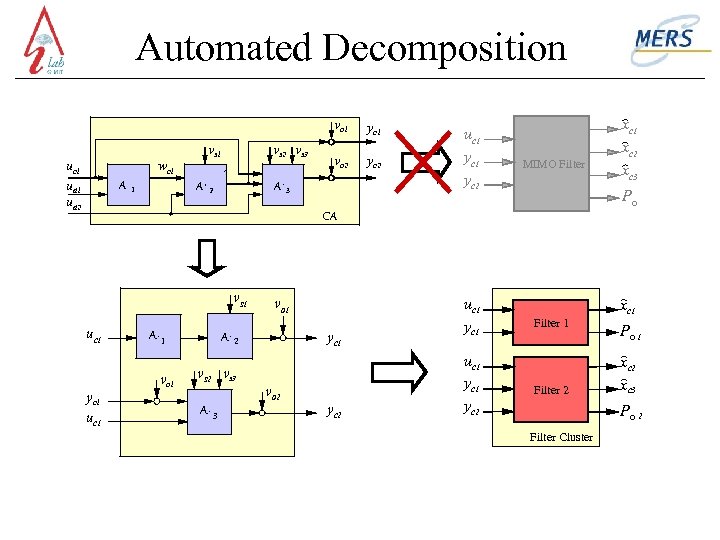
Automated Decomposition vo 1 uc 1 ud 2 vs 1 wc 1 A A 1 vs 2 vs 3 2 A yc 1 vo 2 yc 2 3 uc 1 yc 2 MIMO Filter xc 1 xc 2 xc 3 PO CA vs 1 uc 1 yc 1 uc 1 A A 1 vo 1 3 yc 1 2 vs 3 A vo 1 vo 2 yc 2 uc 1 yc 2 xc 1 Filter 2 PO 1 xc 2 xc 3 PO 2 Filter Cluster

To Address the Scope of Mars 98 Polar Lander Leading Diagnosis: • Legs deployed during descent. • Noise spike on leg sensors latched by software monitors. • Laser altimeter registers 50 ft. • Begins polling leg monitors to determine touch down. • Latched noise spike read as touchdown. • Engine shutdown at ~50 ft. Responding to the failures of Mars Polar Lander and Mars Climate Orbiter is a Hybrid control problem. Idea: Support programmers with embedded languages that avoid commonsense mistakes, by reasoning from hardware models. Reactive Model-based Programming
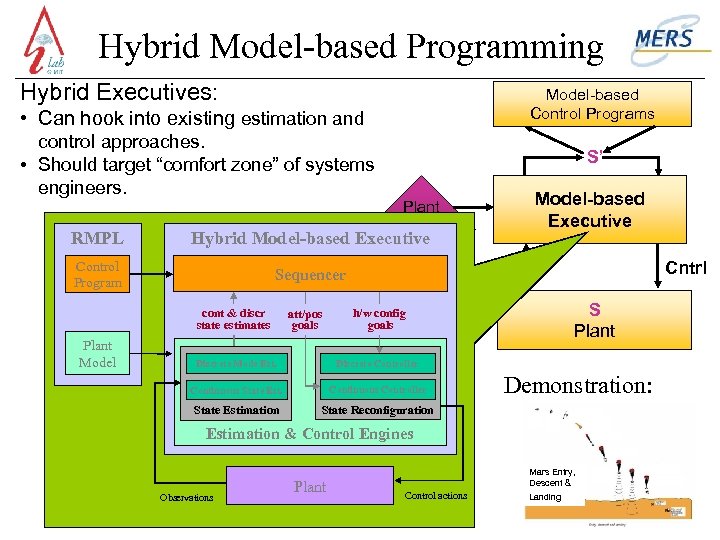
Hybrid Model-based Programming Hybrid Executives: Model-based Control Programs • Can hook into existing estimation and control approaches. • Should target “comfort zone” of systems engineers. S’ Model-based Executive Plant Model RMPL Hybrid Model-based Executive Control Program Sequencer cont & discr state estimates Plant Model att/pos goals Cntrl Obs S Plant h/w config goals Discrete Mode Est. Discrete Controller Continuous State Est. Continuous Controller State Estimation State Reconfiguration Demonstration: Estimation & Control Engines Observations Plant Mars Entry, Descent & Control actions Landing

Recent Publications Hybrid Mode Estimation: • Hofbaur, M. W. and B. C. Williams, “Mode Estimation of Probabilistic Hybrid Systems, ” International Conference on Hybrid Systems: Computation and Control, March, 2002. Hybrid Expectation Maximization (preliminary): • Melvin Henry, Simulators that Learn: Automated Estimation of Hybrid Automata, June 2002 Hybrid Decomposition: • Hofbaur, M. W. and B. C. Williams, “Hybrid Diagnosis with Unknown Behavioral Modes, ” International Workshop on Principles of Diagnosis, Austria, May 3 -5 2002.
c4b8fc18a9cf54bf73a9e042c12f7416.ppt