Модель атома Томсона В 1903 г Дж

Модель атома Томсона. • В 1903 г. Дж. Томсон предложил модель атома, согласно которой атом представляет собой равномерно заполненный положительным электричеством шар, внутри которого находится электрон. Суммарный положительный заряд шара равен заряду электрона, так что атом в целом нейтрален.

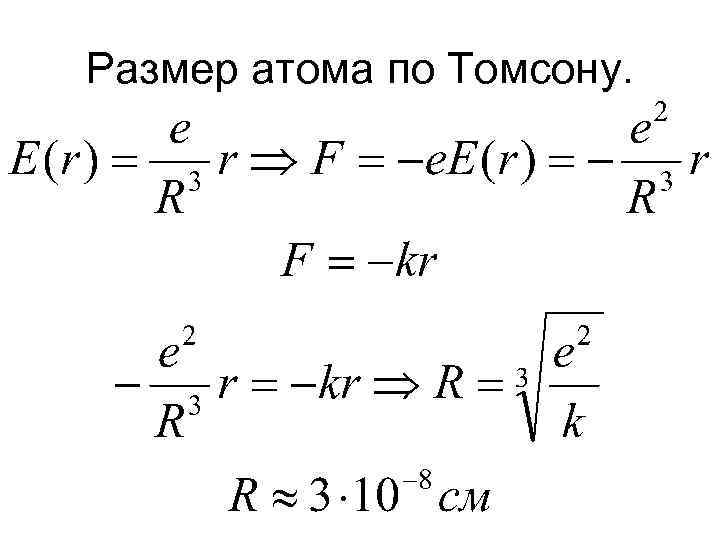Размер атома по Томсону.

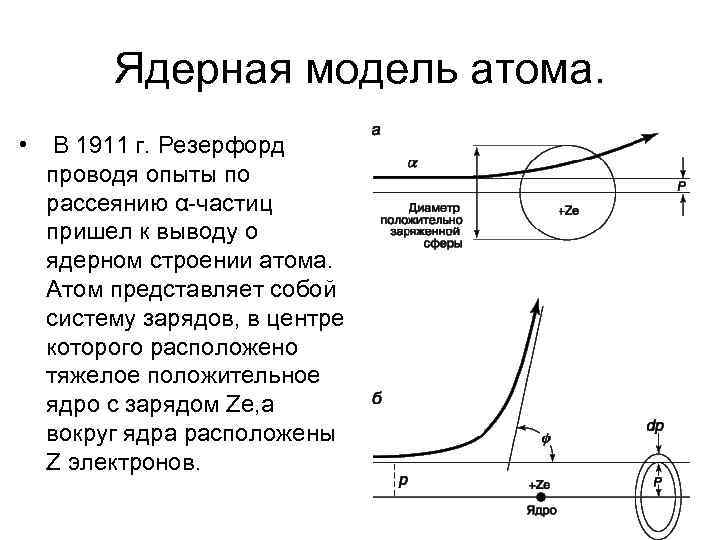Ядерная модель атома. • В 1911 г. Резерфорд проводя опыты по рассеянию α-частиц пришел к выводу о ядерном строении атома. Атом представляет собой систему зарядов, в центре которого расположено тяжелое положительное ядро с зарядом Ze, а вокруг ядра расположены Z электронов.

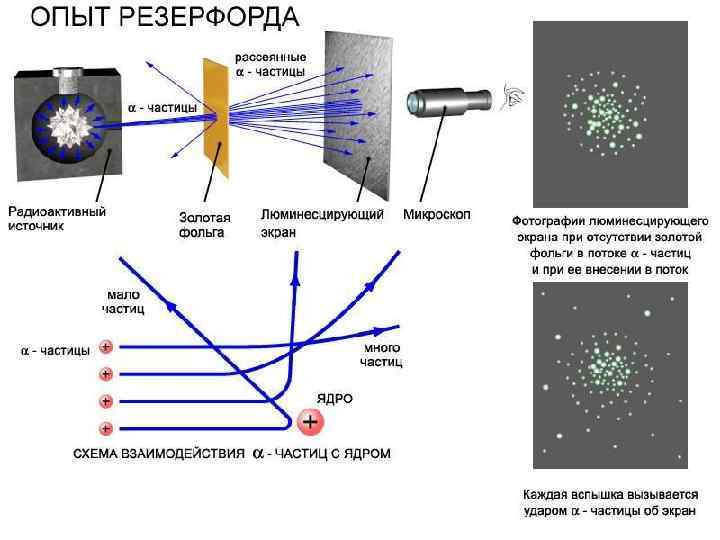
Размер атома по Резерфорду.

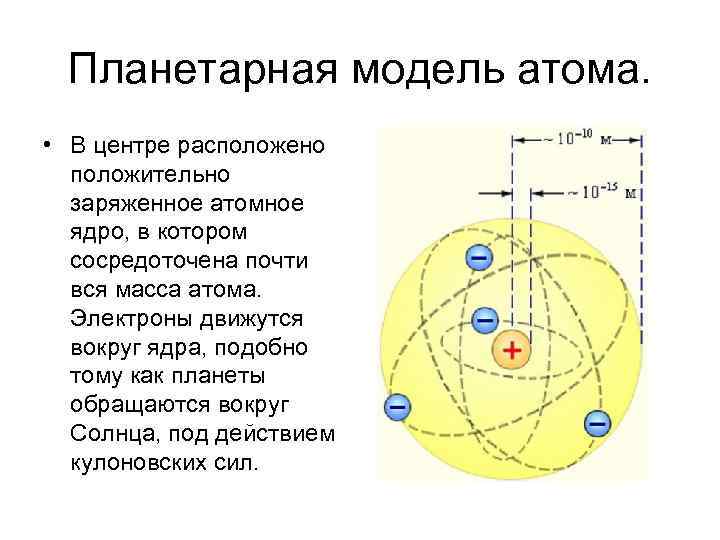Планетарная модель атома. • В центре расположено положительно заряженное атомное ядро, в котором сосредоточена почти вся масса атома. Электроны движутся вокруг ядра, подобно тому как планеты обращаются вокруг Солнца, под действием кулоновских сил.

Спектральный анализ. Теория Кирхгофа и Бунзена позволила изучать строение тел или атомов с помощью его спектра (спектрального анализа). Три разновидности спектров: линейчатые, полосатые и сплошные. Излучение свободных электронов порождает сплошной спектр. Линейчатые или дискретные спектры возникают в результате электронных переходов внутри атомов. Полосатые или молекулярные спектры обусловлены изменением энергии (колебательной и вращательной) внутри молекул.

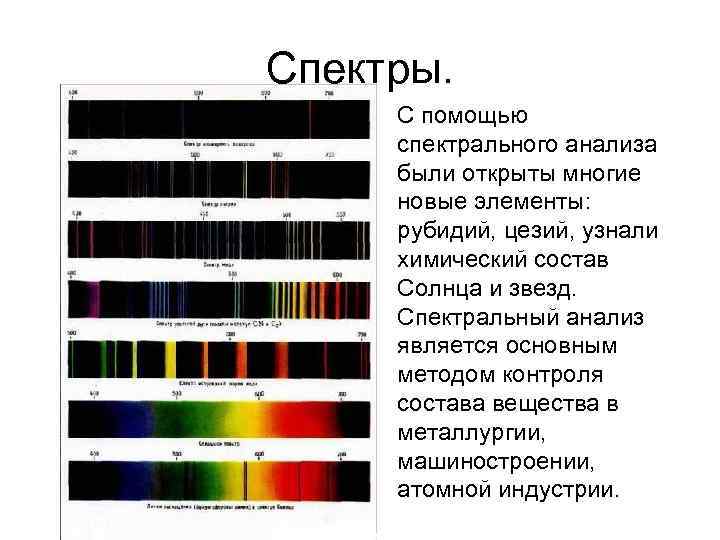Спектры. С помощью спектрального анализа были открыты многие новые элементы: рубидий, цезий, узнали химический состав Солнца и звезд. Спектральный анализ является основным методом контроля состава вещества в металлургии, машиностроении, атомной индустрии.

Постулаты Нильса Бора. • Атомы, несмотря на то что электроны в них движутся с ускорением, могут длительно находиться в состояниях, в которых они не излучают. Эти состояния получили название стационарных или разрешенных. • Энергия атома меняется не непрерывно, а принимает набор дискретных значений. • При переходе атома из одного стационарного состояния в другое атом либо излучает, либо поглощает квант энергии.

• Состояние атома, которому соответствует наименьшая энергия, называют основным состоянием, а состояния, которым соответствуют более высокие энергии, возбужденными. • Реализуются только те стационарные орбиты, для которых справедливо равенство

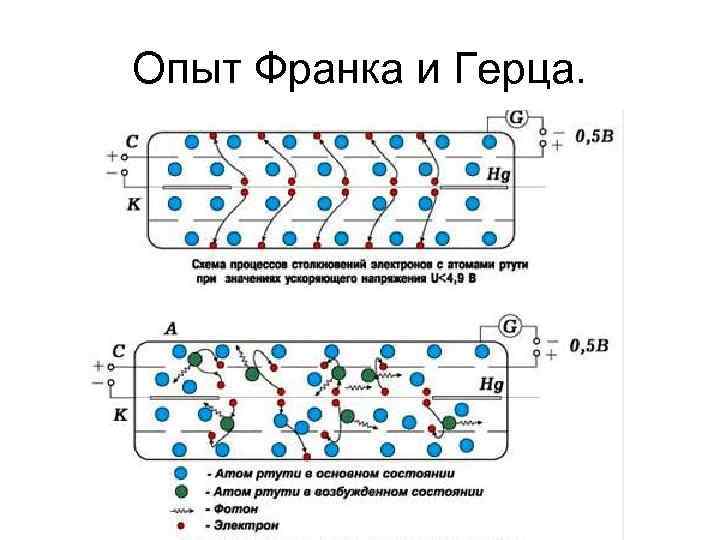Опыт Франка и Герца.

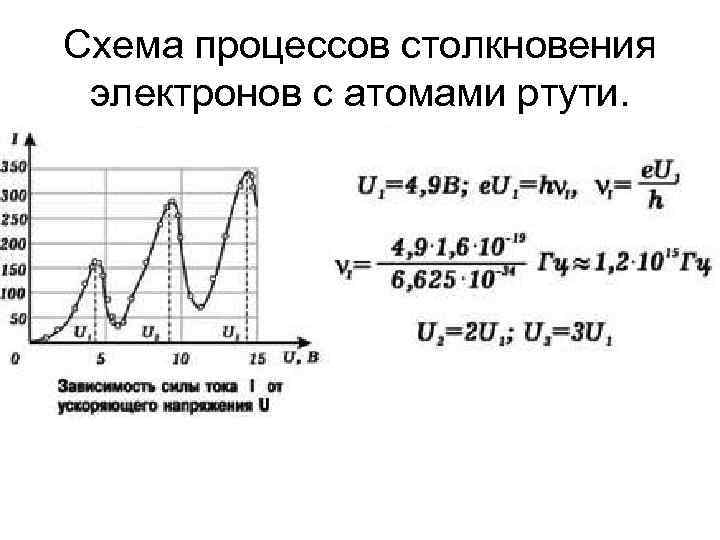Схема процессов столкновения электронов с атомами ртути.

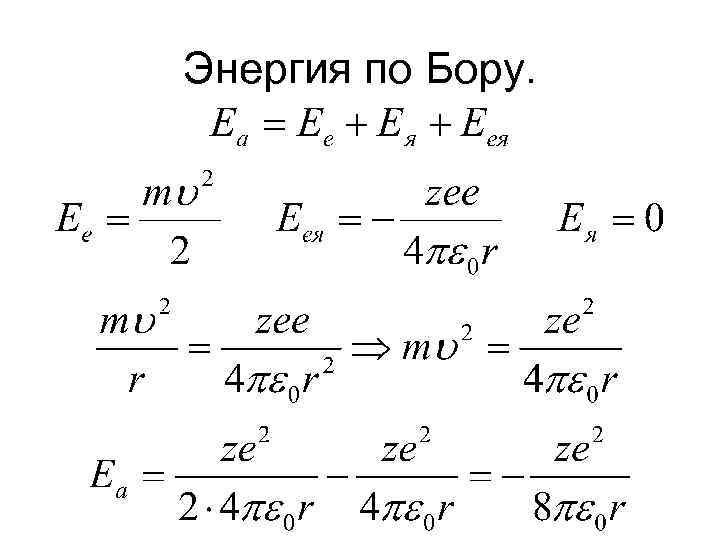Энергия по Бору.

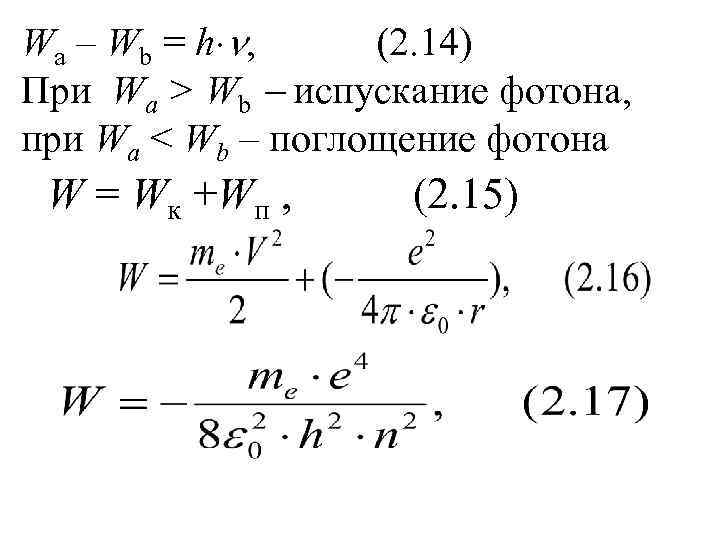Wa – Wb = h , (2. 14) При Wa > Wb испускание фотона, при Wa < Wb – поглощение фотона W = Wк +Wп , (2. 15)

W = - R h/n 2, = (Wа – Wb)/h, (2. 18) (2. 19)

Линейчатый спектр атома водорода где R-постоянная Ридберга (3, 29 1015 с-1) n = 3, 4, 5, . . серия Бальмера где - n 1 и n 2 некоторые целые числа, Т(n 2) и T(n 1) – спектральные термы.

Серия Пашена где n = 4, 5, 6, … Серия Лаймана где n = 1, 2, 3, . . где n и m – целые числа

Теория строения атома по Бору n = 1, 2, 3, . . - главное квантовое числ me - масса электрона, V - скорость электрона, r - радиус круговой орбиты

Условие устойчивости атома

2 =1 r 1 : r 2 : r 3 : . rn : : : (2. 10) -12 Ф/м; о = 8, 85 10 h = 6, 625 10 -34 Дж с; e = 1, 6 10 -19 Кл; me = 9, 1 10 -31 кг rn = r 1 2, n 2 2 2 3 2, …n (2. 11) где r 1 - радиус 1 -й боровской орбиты атома водорода, r 1 = 5, 29 10 -11 м.

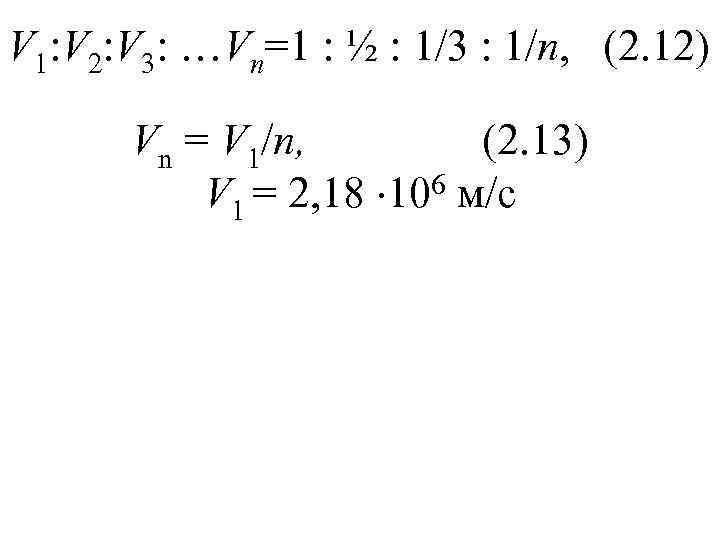V 1: V 2: V 3: …Vn=1 : ½ : 1/3 : 1/n, (2. 12) Vn = V 1/n, (2. 13) V 1 = 2, 18 106 м/с

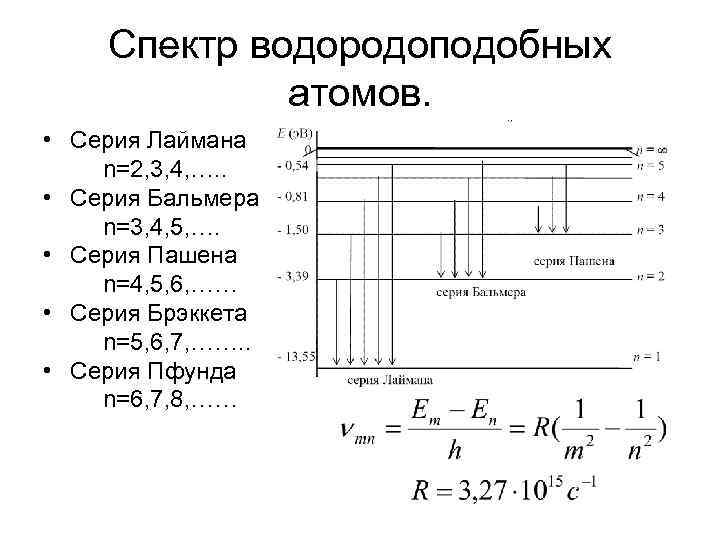Спектр водородоподобных атомов. • Серия Лаймана n=2, 3, 4, …. . • Серия Бальмера n=3, 4, 5, …. • Серия Пашена n=4, 5, 6, …… • Серия Брэккета n=5, 6, 7, ……. . • Серия Пфунда n=6, 7, 8, ……

Радиус Боровский орбит.

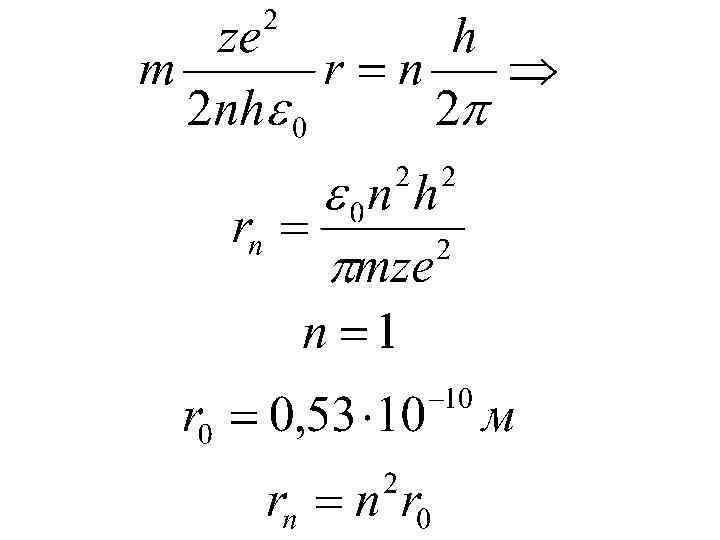
Трудности теории Бора. Теория Бора является половинчатой, внутренне противоречивой. С одной стороны, как мы видели, при построении теории атома водорода используются обычные законы механики Ньютона и давно известный закон Кулона, а с другой – вводятся квантовые постулаты, никак не связанные с механикой Ньютона и электродинамикой Максвелла. Наибольший успех теория имела применительно к атому водорода, для которого оказалось возможным построить количественную теорию спектра. Однако построить количественную теория для следующего за водородом атома гелия не удалось. Возникла необходимость построение новых теоретических представлений о природе внутренней структуры тел и частиц – квантовой механики и квантовой электродинамики.

Корпускулярно-волновые свойства вещества. Элементы квантовой механики.

Природа света? • Свет – волна -интерференция - дифракция • Свет – поток частиц (корпускул) -фотоэффект -эффект Комптона - световое давление

Принцип соответствия. Классическая физика Квантовая физика Специальная теория относительности

Гипотеза де Бройля. • В 1924 г. Луи де Бройль выдвинул гипотезу о волновых свойствах частиц материи, пытаясь ответить на вопрос « в оптике в течение столетия слишком пренебрегали корпускулярными способом рассмотрения по сравнению с волновым; не делалась ли в теории вещества обратная ошибка? »

Гипотеза де Бройля при V << c

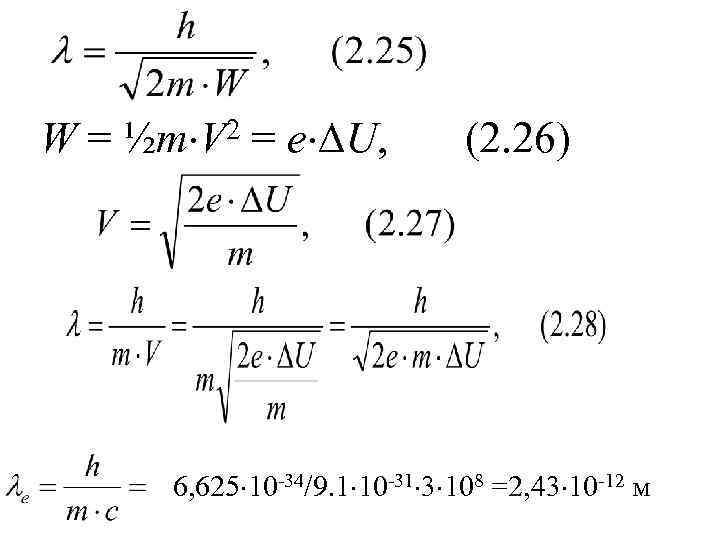W= 2 ½m V = e U, (2. 26) 6, 625 10 -34/9. 1 10 -31 3 108 =2, 43 10 -12 м

Дифракция рентгеновского излучения и электронов. для алюминия.

Вероятностный смысл волн де Бройля Волновая функция или пси-функция (x, y, z, t) = (x, y, z) (t), (2. 30) dw = | |2 d. V = | |2 dx dy dz, (2. 31) w = dw/d. V = 2, | |2 dx dy dz = 1, (2. 32) (2. 33)

Принцип неопределенностей Гейзенберга x px h, y py h, z pz h; (2. 34) где x, y, z – интервалы координат, px, py, pz – проекции импульса

Уравнение Шредингера где W – полная энергия частицы, U – потенциальная энергия частицы, - координатная (амплитудная) часть волновой функции, 2 - оператор Лапласа, 2 = ( 2/ x 2 + 2/ y 2 + 2/ z 2).

Электрон в потенциальном «ящике» U =0 (0 x L), U = (x 0, x L) (2. 38) Если принять ( 2 = d 2/dx 2) (2. 39), то d 2 /dx 2 +(8 2 m/h 2)(W–U) = 0. (2. 40) (х = 0) = (х = L) = 0. (2. 41) Обозначив d 2 /dx 2 = , (2. 42) получим / =- (8 2 m/h 2)(W–U) (2. 43) В области (0 x L), U = 0 (2. 44) При x 0 и x L, U (2. 45)

= 0, | |2 = 0 вне области (0 x L) при краевых условиях (х = 0) = (х = L) = 0 обозначим = k 2, (2. 47), где k – волновое число волны де Бройля

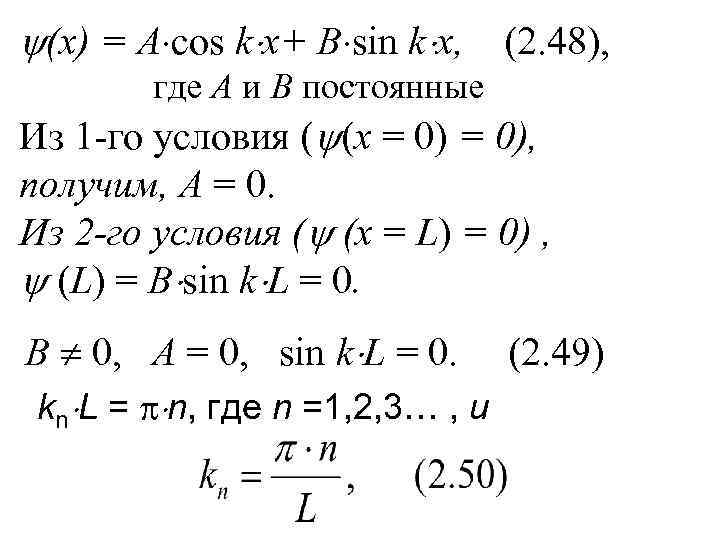(х) = А cos k x+ B sin k x, (2. 48), где А и В постоянные Из 1 -го условия ( (х = 0), получим, А = 0. Из 2 -го условия ( (х = L) = 0) , (L) = B sin k L = 0. В 0, А = 0, sin k L = 0. (2. 49) kn L = n, где n =1, 2, 3… , и

По определению где n – длина волны де Бройля для электрона в «ящике» , то получаем

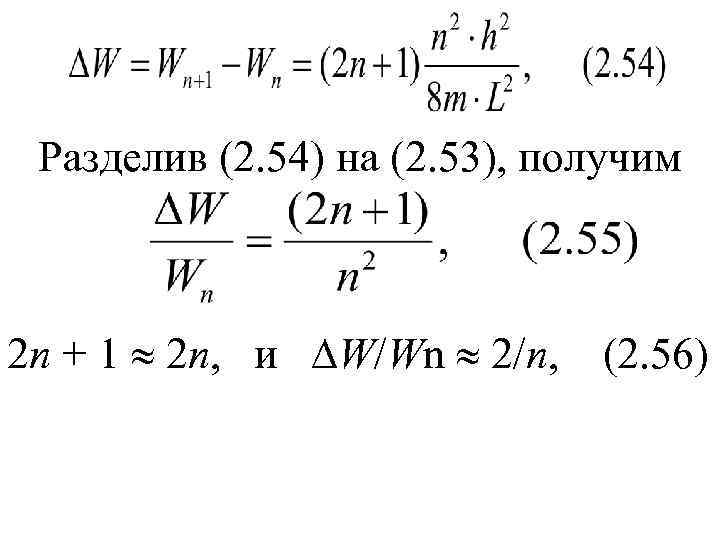Разделив (2. 54) на (2. 53), получим 2 n + 1 2 n, и W/Wn 2/n, (2. 56)

Линейный гармонический осциллятор F = - kx, (2. 59) где k -коэффициент квазиупругой силы, m - масса частицы, o-собственная циклическая частота, k = m o 2, U(x) = ½ k x 2, (2. 60) (2. 61) x = a, где а – амплитуда колебаний

w(x)dx = 2 dt/T, (2. 62) Т период колебаний осциллятора при х а, (2. 63) по соотношению неопределенностей рх = h/a, (2. 64) р рх h/a, (2. 65) W ½ h , (2. 67)

нулевая энергия осциллятора Wо ½ h о, (2. 68) Для гелия ( о 1/m ) (2. 69) Атом водорода в квантовой механике

где n=1, 2, 3, . . , где l - орбитальное квантовое число, l = 0, 1, 2, …, n – 1 l = 0 s–состояние, l =1 p–состояние, l = 2 d-состояние, l = 3 f-состояние n = 2 (l = 0, l = 1); n = 3 (l = 0, l = 1, l = 2)

dw = | 2 d. V | = | 24 | 2 dr, r (2. 74) (2. 75) где m = 0, 1, 2, … l магнитное квантовое число, s-sharp, p-principal, d-diffuse, f-fundamental где s – спиновое квантовое число 2 s + 1 = 2, значит, s = ½,

Lsz = ½ ћ или ms = ½, (2. 77) ms – магнитное спиновое число Принцип Паули. Распределение электронов по уровням Z 1 (n, l, m, ms) = 0 или 1, (2. 78) Z 2 (n, l, m) = 2, (2. 79) Z 3 (n, l) = 2(2 l + 1), (2. 80)

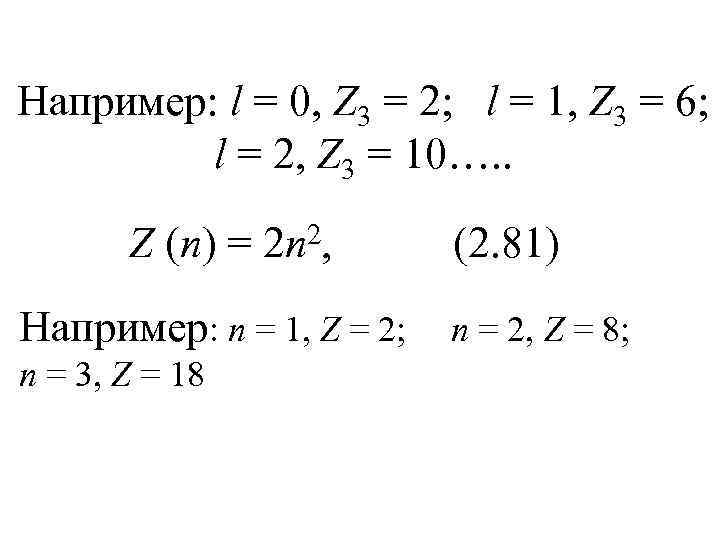Например: l = 0, Z 3 = 2; l = 1, Z 3 = 6; l = 2, Z 3 = 10…. . Z (n) = 2, 2 n Например: n = 1, Z = 2; n = 3, Z = 18 (2. 81) n = 2, Z = 8;

Заданные n, l, n, l n квантовые m, ms m числа Максимальное 1 2 2(2 l + 1) 2 n 2 число электронов

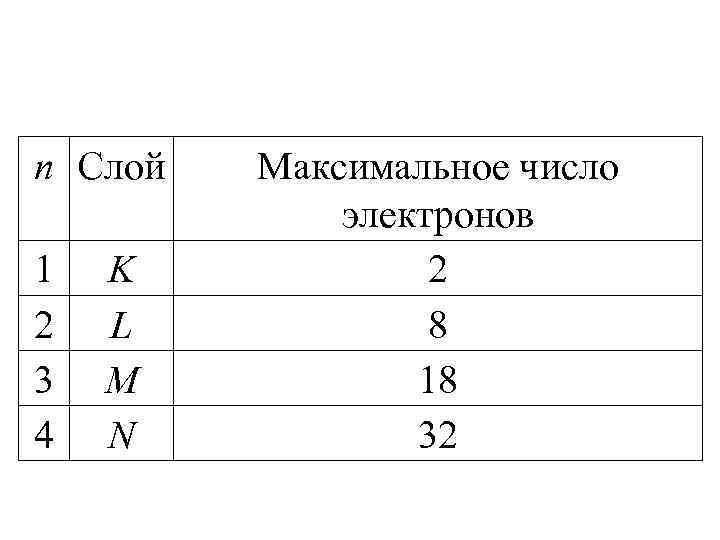n Слой 1 2 3 4 K L M N Максимальное число электронов 2 8 18 32

Периодическая система элементов Д. И. Менделеева Кислород: О - 1 s 2 2 p 4 Физическая природа химической связи. Молекула водорода

Строение атомного ядра Заряд ядра Ze, где e – заряд протона, Z – порядковый номер элемента число нейтронов N Z, массовое число A = N + Z, (2. 86)

Условное обозначение ядра: ZXA, где X – химический элемент Z 1 = Z 2, A 1 A 2 – изотопы, (2. 87) Z 1 Z 2, A 1= A 2 – изобары, (2. 88) R = R 0 A⅓, где R 0 = (1, 3 1, 5)10 -15 м Z 1=Z 2, A 1=A 2, Т 1/2–изомеры, (2. 89)

где I внутреннее спиновое квантовое число: 0, ½, 1, 3/2, и т. д. Капельная модель – Френкель (1939), Оболочная модель – Гепперт-Майер, Магические ядра: 2, 8, 20, 28, 50, 82, 126. Дважды магические ядра: He 4, 8 O 16, 20 Ca 40, 20 Ca 48, 82 Pb 208 2

Масса и энергия связи m = Wсв/c 2, (2. 91) – дефект массы m = Z·mp + (A-Z)·mn – Mя, (2. 92) где Z и mp – число и масса протонов, (A-Z) и mn – число и масса нейтронов, Mя – масса ядра, m = Zm. H + (A-Z)mn – Mа, (2. 93)

Wсв = mc 2 =Zmp + (A-Z)mn – Mя]c 2, (2. 94) Wсв= mc 2 =[Zmp +(A-Z)mn – Mя]c 2, (2. 94) wсв в среднем 8 Мэ. В/нуклон Электронные, колебательные и вращательные состояния молекул We – электронная энергия, Wv–колебательная (вибрационная) энергия, Wr–вращательная (ротационная) энергия

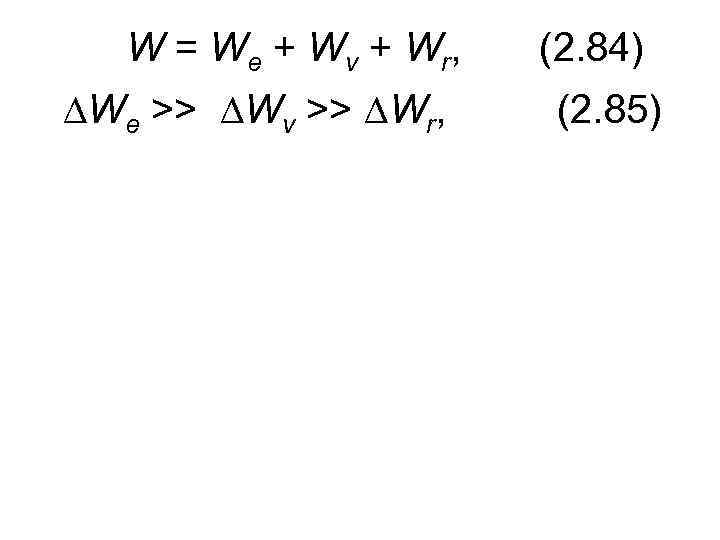W = W e + W v + W r, We >> Wv >> Wr, (2. 84) (2. 85)

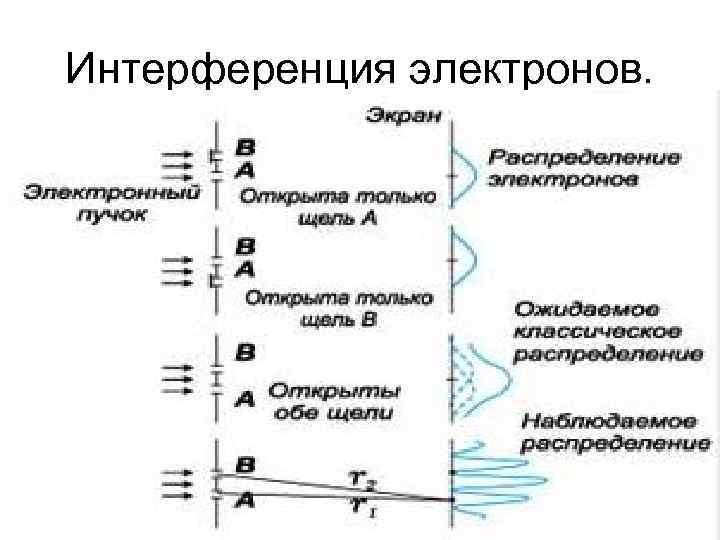Интерференция электронов.

Эффект Комптона - Комптоновская длина волны

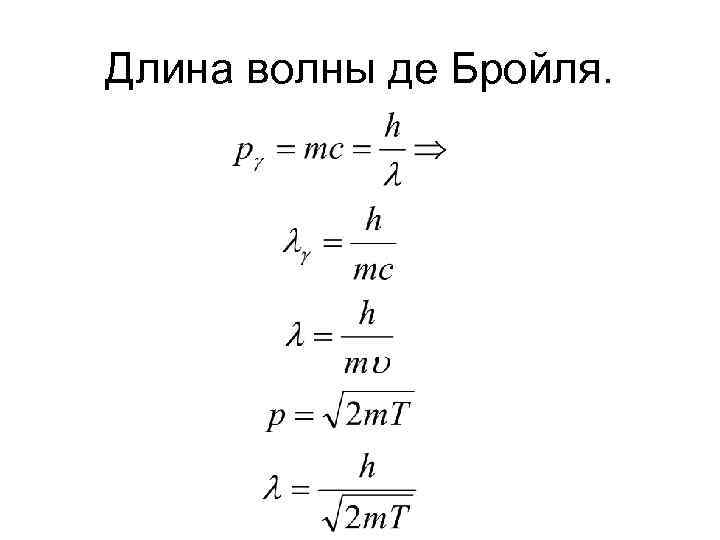Длина волны де Бройля.

Границы частиц и волн. Нерелятивистский случай: Релятивистский случай:

Принцип неопределенности. • В классической механике состояние материальной точки (частицы) определяется заданием значений координат, импульса, энергии (динамическими переменными). В квантовой физики изучают микрочастицы, понимая под ними элементарные частицы (электроны, протоны, нейтроны, фотоны) и сложные частицы состоящие из небольшого числа элементарных частиц (молекулы, атомы). Микрочастицы реальны, но «потрогать» или увидеть их нельзя. Следовательно для них нельзя однозначно определить динамические величины. О существовании микрочастиц мы судим о их взаимодействии с макротелами, т. е. их характеристики состояний можно определять через привычные для нас величины.

Принцип Гейзенберга.

Соотношение неопределенности координаты и энергии.

Соотношение неопределенности является одним из фундаментальных положений квантовой механики. Одного этого соотношения достаточно, чтобы получить ряд важных результатов: в частности, оно позволяет объяснить тот факт, что электрон не падает на ядро атома, а также оценить размеры простейшего атома (водорода) и минимальную возможную энергию электрона в таком атоме. Если бы электрон упал на точечное ядро, его координаты и импульс приняли бы определенные (нулевые) значения, что несовместимо с принципом неопределенности.

Соотношение неопределенности и постулаты Бора.

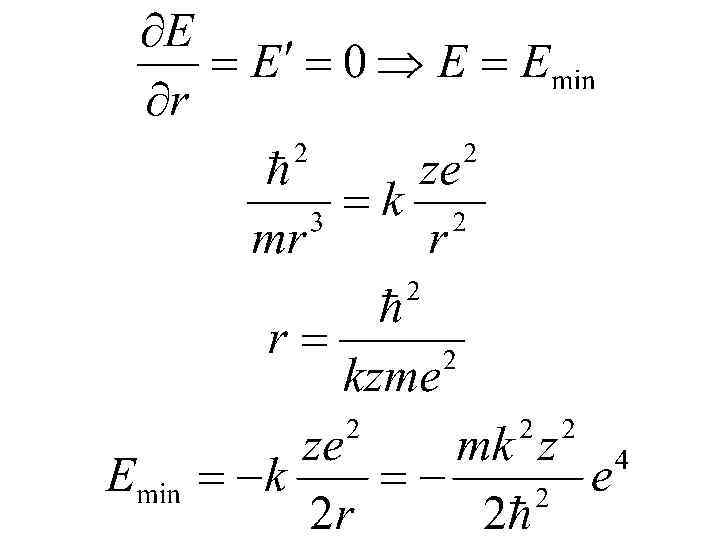
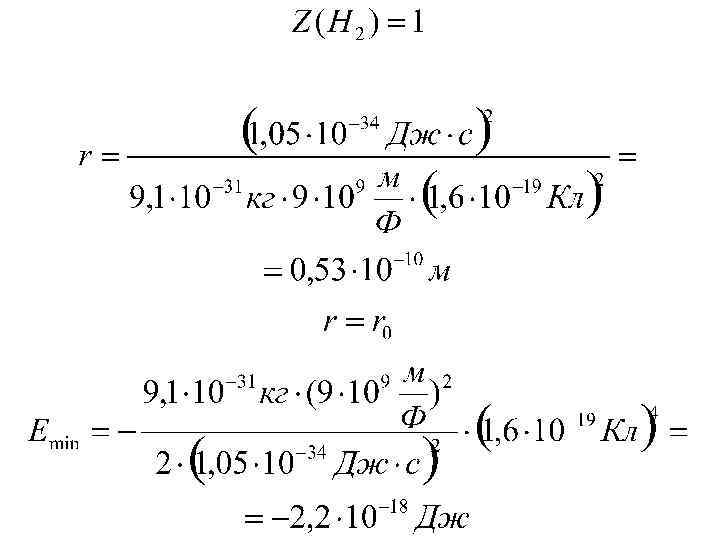
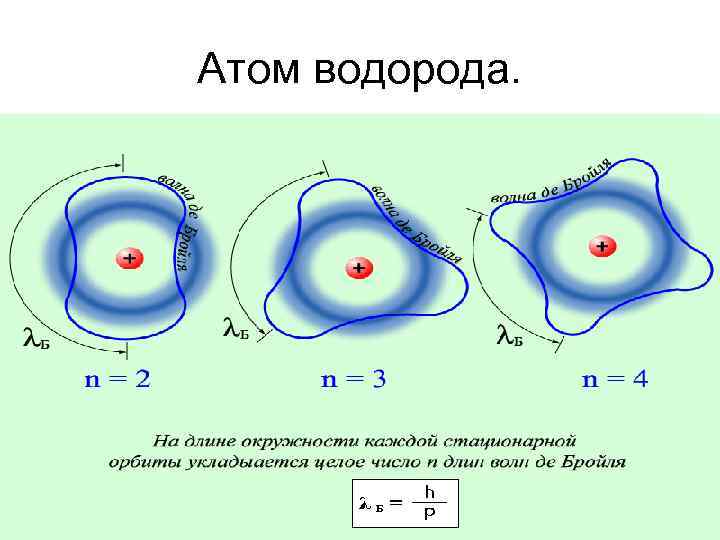Атом водорода.

Волна де Бройля абстрактный объект, увидеть его или зарегистрировать её невозможно. Частицы двигаются не по законам Ньютона, а по некоторым волновым законам. При этом волна имеет вероятностный смысл, зная её можно определить вероятность нахождения частицы в конкретный момент времени в конкретной точки пространства.