МОДЕЛЬ АТОМА ДЖ ТОМСОНА ПЛАНЕТАРНАЯ МОДЕЛЬ АТОМА РЕЗЕРФОРДА

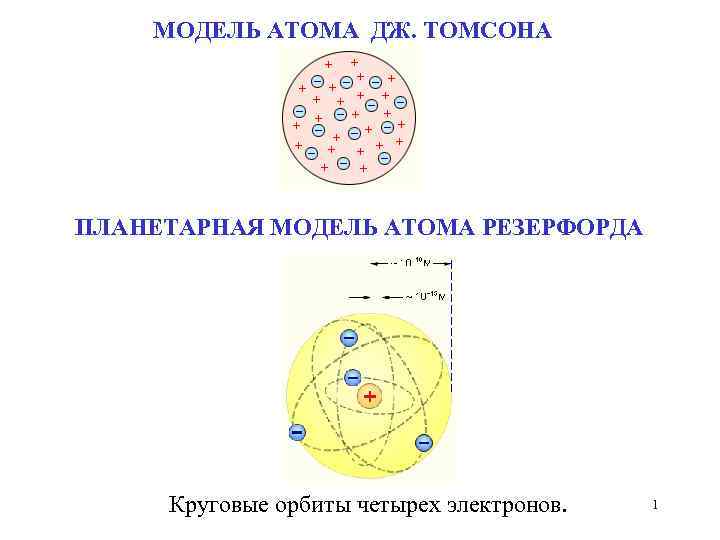МОДЕЛЬ АТОМА ДЖ. ТОМСОНА ПЛАНЕТАРНАЯ МОДЕЛЬ АТОМА РЕЗЕРФОРДА Круговые орбиты четырех электронов. 1

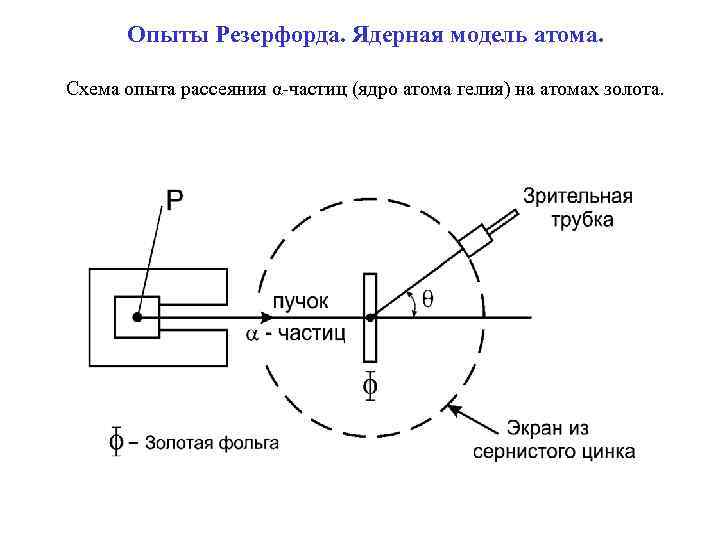Опыты Резерфорда. Ядерная модель атома. Схема опыта рассеяния α-частиц (ядро атома гелия) на атомах золота.

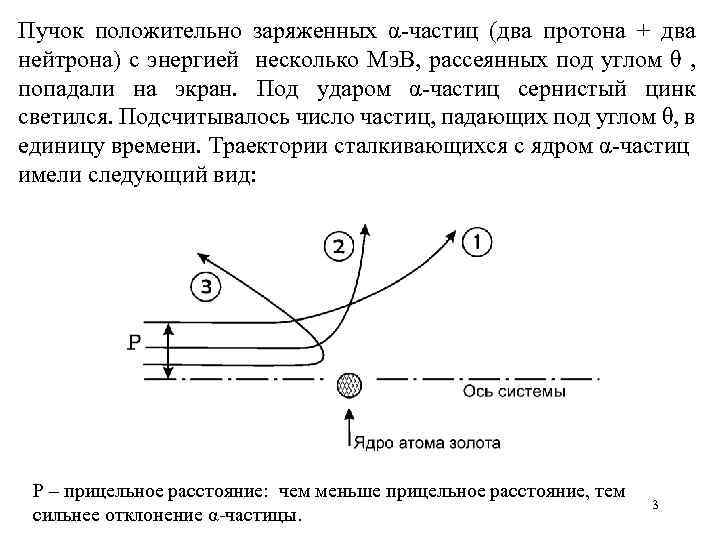Пучок положительно заряженных α-частиц (два протона + два нейтрона) с энергией несколько Мэ. В, рассеянных под углом θ , попадали на экран. Под ударом α-частиц сернистый цинк светился. Подсчитывалось число частиц, падающих под углом θ, в единицу времени. Траектории сталкивающихся с ядром α-частиц имели следующий вид: Р – прицельное расстояние: чем меньше прицельное расстояние, тем сильнее отклонение α-частицы. 3

Выводы из опытов: 1. Весь положительный заряд атома сосредоточен в очень малой области с диаметром d ~ 10 -15 м. 2. Число элементарных положительных зарядов ядра совпадает с порядковым номером Z элемента в периодической таблице элементов Менделеева. 3. Был определен верхний предел размеров ядра. Он следовал из законов сохранения энергии. Для золота: 4

4. Построена ядерная модель атома: в ядре атома ~10 -14 -10 -15 м сосредоточен весь положительный заряд. В области размером ~10 -10 м движутся электроны. Противоречивость модели: ускоренное движение электрона в атоме должно приводить к излучению и он должен упасть на ядро! Тогда как эксперименты указывают, что: 1. Атом является устойчивой системой. 2. Излучение появляется при определенных условиях. 3. Излучение имеет линейчатый спектр. 5

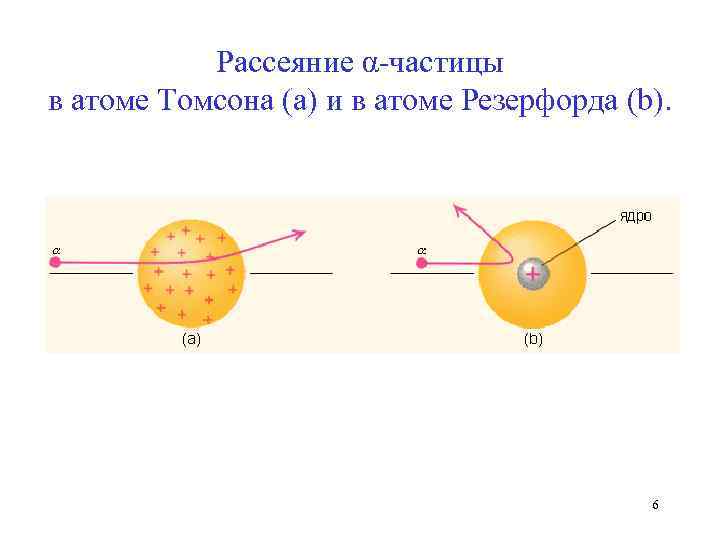Рассеяние α-частицы в атоме Томсона (a) и в атоме Резерфорда (b). 6

СПЕКТР АТОМА ВОДОРОДА В начале XIX века были открыты дискретные спектральные линии в излучении атома водорода в видимой области (так называемый линейчатый спектр). В 1890 году И. Ридберг получил эмпирическую формулу для частот спектральных линий: R - постоянная Ридберга, R = 3, 29· 1015 Гц. Для серии Бальмера (видимый свет) m = 2, n = 3, 4, 5, . . Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4, … В инфракрасной области спектра: серия Пашена m = 3, n = 4, 5, 6, … серия Брэкета m = 4, n = 5, 6, 7, … серия Пфунда m = 5, n = 6, 7, 8, . . . , серия Хэмфри m = 6, n = 7, 8, 9, . . .

Диаграмма энергетических уровней атома водорода. Показаны переходы, соответствующие различным спектральным сериям. Для первых пяти линий серии Бальмера в видимой части 8 спектра указаны длины волн.

Теория Бора для водородоподобных атомных систем. В развитие классической модели атома Резерфорда Нильс Бор ввел 3 постулата: 1. Постулат стационарных состояний. Существуют некоторые стационарные состояния атома, находясь в которых он не излучает энергии. 2. Постулат о квантовании орбит. В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантовые значения момента импульса, удовлетворяющие условию: - главное квантовое число. m- масса электрона, - его скорость на орбите радиусом r. PS. Физический смысл постулата: целое число n равно числу длин волн де Бройля движущегося электрона, укладывающихся на длине круговой орбиты(т. е. электрон проявляет волновые свойства!) 9

10

3. Правило частот. При переходе атома из одного стационарного состояния в другое испускается или поглощается один квант энергии энергия электрона в атоме после перехода; энергия до перехода. Если электрон поглощает если света, квант электрон излучает квант света. Основные уравнения теории Бора. Электрон с отрицательным зарядом движется по окружности вокруг центра, в котором расположено положительное ядро с зарядом. 1. Движение по окружности происходит в кулоновском поле: 11

2. Условие квантования момента импульса: Тогда получаем: При n = 1 получаем первый Боровский радиус для атома водорода (z = 1) 3. Потенциальная энергия электрона в атоме имеет дискретный набор значений: 12

4. Полная энергия электрона в атоме состоит из суммы кинетической и потенциальной энергии: Для любых n полная энергия отрицательна и принимает дискретный набор значений. Основное состояние электрона в атоме водорода при n = 1. 13

Стационарные орбиты атома водорода и образование спектральных серий. 14

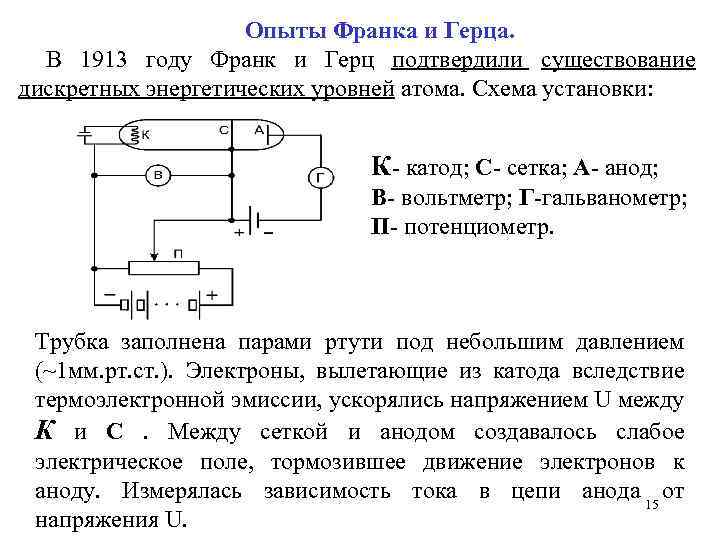Опыты Франка и Герца. В 1913 году Франк и Герц подтвердили существование дискретных энергетических уровней атома. Схема установки: К- катод; С- сетка; А- анод; В- вольтметр; Г-гальванометр; П- потенциометр. Трубка заполнена парами ртути под небольшим давлением (~1 мм. рт. cт. ). Электроны, вылетающие из катода вследствие термоэлектронной эмиссии, ускорялись напряжением U между К и С. Между сеткой и анодом создавалось слабое электрическое поле, тормозившее движение электронов к аноду. Измерялась зависимость тока в цепи анода 15 от напряжения U.

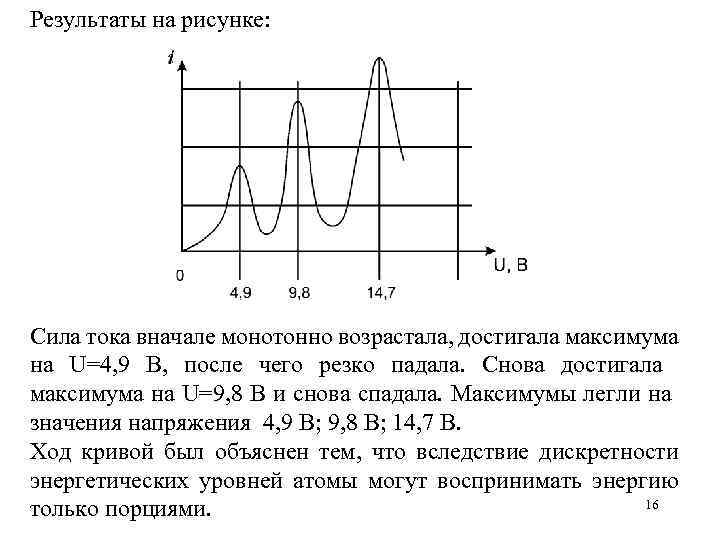Результаты на рисунке: Сила тока вначале монотонно возрастала, достигала максимума на U=4, 9 В, после чего резко падала. Снова достигала максимума на U=9, 8 В и снова спадала. Максимумы легли на значения напряжения 4, 9 В; 9, 8 В; 14, 7 В. Ход кривой был объяснен тем, что вследствие дискретности энергетических уровней атомы могут воспринимать энергию 16 только порциями.

и т. д. энергии 1 -го, 2 -го, 3 -го и т. д. стационарных где состояний. Вывод: при столкновении электрона с атомом ртути возможно два исхода: 1. Упругий удар (энергия электрона меньше ) 2. Неупругий удар (энергия электрона больше ) При ударе 2 -го типа, атом поглощает энергию электрона, а затем ее переизлучает. Таким образом, эксперименты подтвердили постулаты Бора и позволили вычислить постоянную Ридберга. Но появились новые трудности: 1. Не удается объяснить интенсивность спектральных линий. 2. Формулы хорошо описывают излучение атома водорода и водородоподобных ионов, они на дают возможность применить их для сложных атомов. 17