Model 4 The Nut Company and the Simplex

Model 4: The Nut Company and the Simplex Method AJ Epel Thursday, Oct. 1

Contents l The Problem l Assumptions and Constraints l The Linear Program l Step-by-step Review: Simplex Method l Solution by Computer l Conclusion

The Problem l Three different blends for sale ¡ Regular - sells for $0. 59/lb ¡ Deluxe - sells for $0. 69/lb ¡ Blue Ribbon - sells for $0. 85/lb l Four kinds of nuts can be ¡ Almonds - costs $0. 25/lb ¡ Pecans - costs $0. 35/lb ¡ Cashews - costs $0. 50/lb ¡ Walnuts - costs $0. 30/lb mixed in each

The Problem l How should the company maximize weekly profit? l What amounts of each nut type should go into each blend? l Use a linear model!

Assumptions and Constraints l Non-negative quantities of nuts and blends l Continuous model: fractions okay l Costs, quantities supplied constant from week to week l Can sell all blends made at their listed selling prices l Not every nut needs to be in each blend

Assumptions and Constraints l Max. quantities of supplied nuts ¡ Almonds: 2000 lbs. altogether ¡ Pecans: 4000 lbs. altogether ¡ Cashews: 5000 lbs. altogether ¡ Walnuts: 3000 lbs. altogether

Assumptions and Constraints l Proportions of one nut to the whole blend ¡ Regular l l l ¡ Deluxe l l ¡ No more than 20% cashews No more than 25% pecans No less than 40% walnuts No more than 35% cashews No less than 25% almonds Blue Ribbon l l l No more than 50% cashews No less than 30% almonds

The Linear Program l Let Xjk = quantity of nut type j in blend k l Let Mjk = margin for nut type j in blend k l Let π = profit to company l So π = for k = 1. . . 3 for j = 1. . . 4 (Mjk. Xjk)

The Linear Program l On ¡J future slides, Xjk may be written as Jk is the nut type: A(lmond), P(ecan), C(ashew), W(alnut) ¡ k is the blend: r(egular), d(eluxe), b(lue ribbon)

The Linear Program l Quantity constraints ¡ for j = 1. . . 4 Xjk ≤ Max. quantity. for j ¡ Example: Ar + Ad + Ab ≤ 2000 l Proportion constraints ¡ Example: Cr ≤ 0. 2(Ar + Pr + Cr + Wr) ¡ 0. 8 Cr - 0. 2 Ar - 0. 2 Pr - 0. 2 Wr ≤ 0 l “No less than” constraints ¡ Multiply everything by -1

The Linear Program l l l l Max π =. 34 Ar +. 44 Ad +. 6 Ab +. 24 Pr +. 34 Pd +. 5 Pb +. 09 Cr +. 19 Cd +. 35 Cb +. 29 Wr +. 39 Wd +. 55 Wb subject to Ar + Ad + Ab ≤ 2000 Pr + Pd + Pb ≤ 4000 Cr + Cd + Cb ≤ 5000 Wr + Wd + Wb ≤ 3000 -. 2 Ar -. 2 Pr +. 8 Cr -. 2 Wr ≤ 0 -. 25 Ar +. 75 Pr -. 25 Cr -. 25 Wr ≤ 0 -. 35 Ad -. 35 Pd +. 65 Cd -. 35 Wd ≤ 0 -. 5 Ab -. 5 Pb +. 5 Cb -. 5 Wb ≤ 0. 4 Ar +. 4 Pr +. 4 Cr -. 6 Wr ≤ 0 -. 75 Ad +. 25 Pd +. 25 Cd +. 25 Wd ≤ 0. 3 Ab +. 3 Pb -. 7 Cb +. 3 Wb ≤ 0 -. 7 Ab +. 3 Pb +. 3 Cb +. 3 Wb ≤ 0

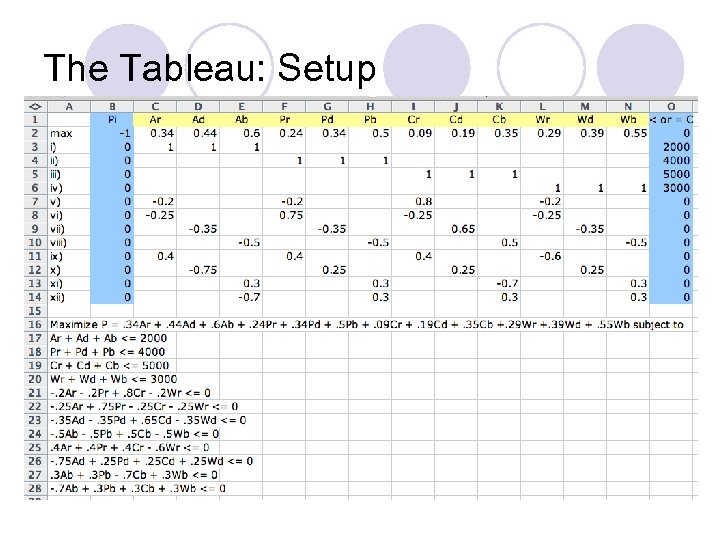The Tableau: Setup

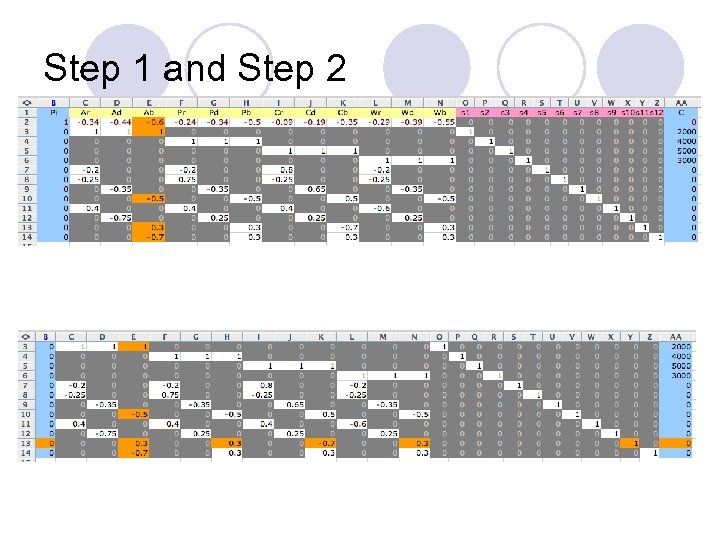Step 1 and Step 2

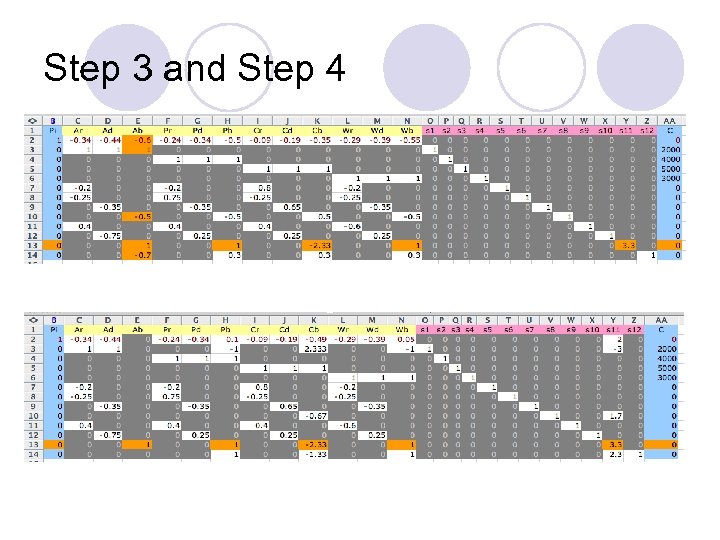Step 3 and Step 4

Solution by Computer

Conclusion l Maximum weekly profit: $4524. 24 l Buy these: ¡ Almonds: 2000 lbs. ¡ Pecans: 4000 lbs. ¡ Cashews: 3121 lbs. ¡ Walnuts: 3000 lbs.

Conclusion l Blend 5455 lbs. of Regular this ¡ 1364 lbs. pecan (25% of blend) ¡ 1091 lbs. cashew (20% of blend) ¡ 3000 lbs. walnut (55% of blend) way: l Eliminate Deluxe blend l Blend 6667 lbs. of Blue Ribbon this way: ¡ 2000 lbs. almond (30% of blend) ¡ 2636 lbs. pecan (39. 55% of blend) ¡ 2030 lbs. cashew (30. 45% of blend)

Conclusion: What if Deluxe can’t be eliminated? l New constraints: ¡ Ar + Pr + Cr + Wr ≥ 1 lb. ¡ Ad + Pd + Cd + Wd ≥ 1 lb. ¡ Ab + Pb + Cb + Wb ≥ 1 lb. l Solved again ¡ Profit = $4524. 14 ($0. 10/week less) ¡ Only 1 lb. of Deluxe manufactured! 75% pecan, 25% almond l 1 less lb. of Blue Ribbon l

Sources used on the Simplex method l l l Shepperd, Mike. "Mathematics C: linear programming: simplex method. ” July 2003. Reveliotis, Spyros. “An introduction to linear programming and the simplex algorithm. ” 20 June 1997. Waner, Stefan and Steven R. Costenoble. “Tutorial for the simplex method. ” May 2000.

Questions?