3f852529f4374cb00cfecbbc8323c49d.ppt
- Количество слайдов: 23

Mobile Computing Group An Introduction to Game Theory part II Vangelis Angelakis 21 / 10 / 2004

Previously on Part I… Game theory is the mathematically founded study of conflict and cooperation. In non-cooperative games cooperation arises, when it is in the best interest of players Rational players do not play dominated strategies. A strategic form game can be a single round of a repeated game Players are in a Nash equilibrium if a unilateral change in strategies by any one of them would lead that player to earn less than if she remained with her current strategy. Under mixed strategies any game in strategic-form has an equilibrium TNL - Mobile Computing Group Angelakis Vangelis 21/10/2004

Extensive games Games in strategic form have no temporal component. Players choose their strategies simultaneously not knowing how other players moved. An extensive form game or game tree is a more detailed model than a normal form game. It represents a formalization of interactions where players can over time be informed about the actions of others. Each player moves at a designated time & order and no simultaneous moves are allowed. In an extensive game of perfect information each player is aware of all the previous choices of all other players. TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

Remember this: Quality Selection Customer Buy Don’t buy 2 1 Vo. IP Provider High 2 0 0 Low TNL - Mobile Computing Group 1 3 Angelakis Vangelis 1 1 21/10/2003
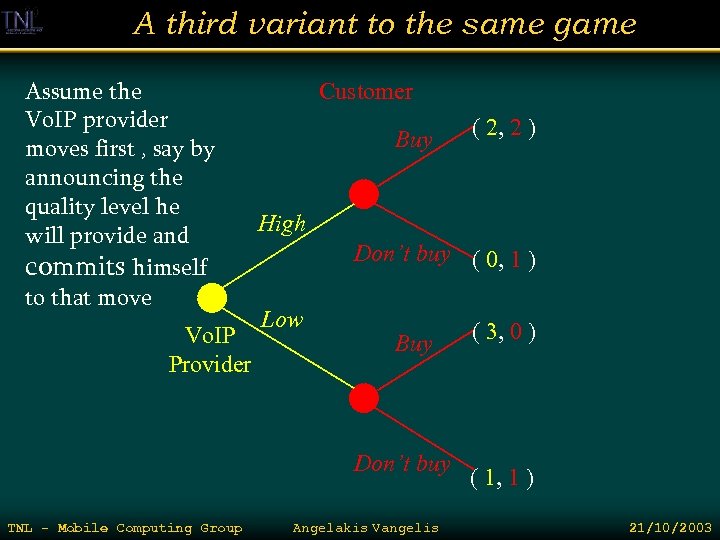
A third variant to the same game Assume the Vo. IP provider moves first , say by announcing the quality level he will provide and commits himself to that move Vo. IP Provider Customer Buy High Don’t buy ( 0, 1 ) Low Buy Don’t buy TNL - Mobile Computing Group ( 2, 2 ) Angelakis Vangelis ( 3, 0 ) ( 1, 1 ) 21/10/2003
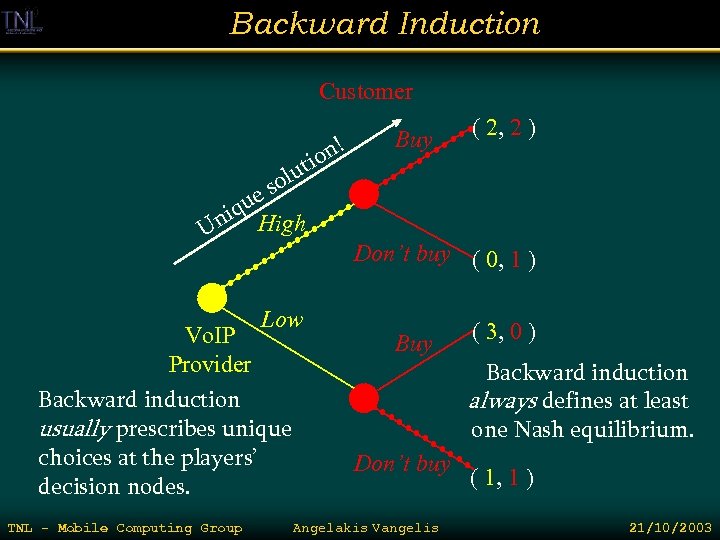
Backward Induction Customer n! tio Buy ( 2, 2 ) olu s ue niq High U Low Vo. IP Provider Backward induction usually prescribes unique choices at the players’ decision nodes. TNL - Mobile Computing Group Don’t buy ( 0, 1 ) Buy Don’t buy Angelakis Vangelis ( 3, 0 ) Backward induction always defines at least one Nash equilibrium. ( 1, 1 ) 21/10/2003
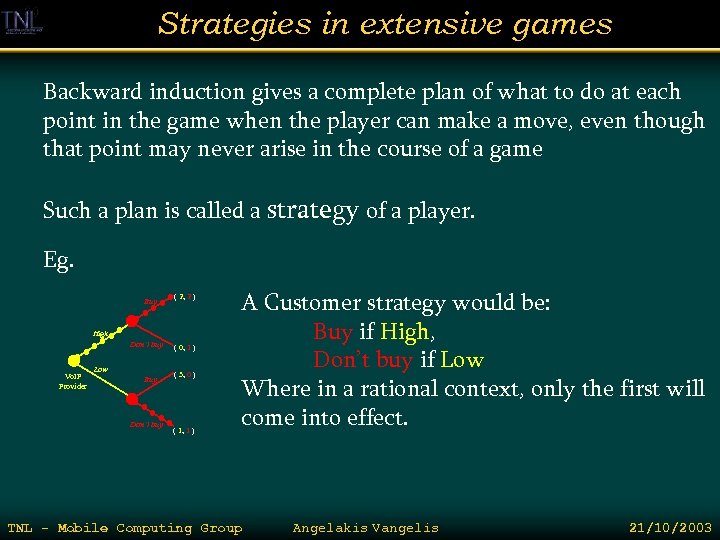
Strategies in extensive games Backward induction gives a complete plan of what to do at each point in the game when the player can make a move, even though that point may never arise in the course of a game Such a plan is called a strategy of a player. Eg. Buy ( 2, 2 ) High Don’t buy Vo. IP Provider Low Buy Don’t buy ( 0, 1 ) ( 3, 0 ) ( 1, 1 ) A Customer strategy would be: Buy if High, Don’t buy if Low Where in a rational context, only the first will come into effect. TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

Strategic forms of extensive games The strategic form of a game tree tabulates all possible strategies of the players All move combinations of the second player must be distinguished as strategies since any two of them could lead to different results depending on the moves of player 1. ( 2, 2 ) High Don’t buy Vo. IP Provider Low Buy Don’t buy ( 0, 1 ) High Buy/Low Buy/High Don’t/Low Don’t/High Buy/Low Don’t /High Don’t/Low 2 Buy Customer Vo. IP Provider 2 1 1 2 ( 3, 0 ) 2 0 Low 3 0 1 1 0 0 3 1 1 ( 1, 1 ) TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

Nash equilibria in extensive games Backward induction always defines a Nash equilibrium But not all possible Nash equilibria of an extensive game arise by backward induction. Don’t/High, Don’t/Low Is a Nash equilibrium, Given the knowledge that player 1 has chosen low. This is a suboptimal solution to a subgame. Customer Vo. IP Provider Buy/High Don’t/Low Don’t/High Buy/Low Don’t /High Don’t/Low 2 High Buy/Low 2 1 1 2 2 0 Low 3 0 1 1 0 0 3 1 1 Backward induction derived Nash equilibria are subgame perfect TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

First mover advantage Many games in strategic form exhibit what is called first-mover advantage A player in a game becomes the first mover or leader when he can commit to a strategy and inform other players about it. First mover advantage states that a player who can become a leader will not be worse off than an original game where all players act simultaneously. Also known as Stackelberg leadership If a player has the power to commit he should do so. TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

First mover advantage “If a player has the power to commit he should do so. ” CAUTION: what happens in the case where more than one players can commit to a move? It is not necessarily best go first… What if player 2 was to be leader? Customer Buy Don’t buy 2 1 Vo. IP Provider High 2 0 0 Low TNL - Mobile Computing Group Angelakis Vangelis 3 1 1 21/10/2003

Chip Duopoly II Solution by dominance gives (M, m) with a utility of 16 for each player. h m n I H 0 0 M 8 12 12 8 L 0 Angelakis Vangelis 0 32 18 18 32 0 36 20 15 20 36 N 18 16 9 9 16 18 TNL - Mobile Computing Group l 0 27 27 0 0 0 21/10/2003

Chip Duopoly with commitment H h 0, 0 m 12, 8 l 18, 9 n 36, 0 h 8, 12 M m 16, 16 l L n 20, 15 32, 0 h 9, 18 m 15, 20 N l n 18, 18 27, 0 h 0, 36 m l 0, 32 n 0, 27 0, 0 Player I has an incentive to commit to strategy H, gaining a utility of 18 and leaving II with 9. TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

Imperfect information Players do not always have full access to all information that is relevant to the choices they make. Situations like this are modeled by extensive games with imperfect information. Eg. Small startup announces the development of a key technological product. A big and well established company that dominates the market is known to have a large R&D dept… But others don’t know what the R&D has come up with… The large company can announce the future release of a competitive product or cede the market. The first is a real or bluff option, where the second will not be in the case the product is within reach. The small company after an announcement can chose either stay in or sell out TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003
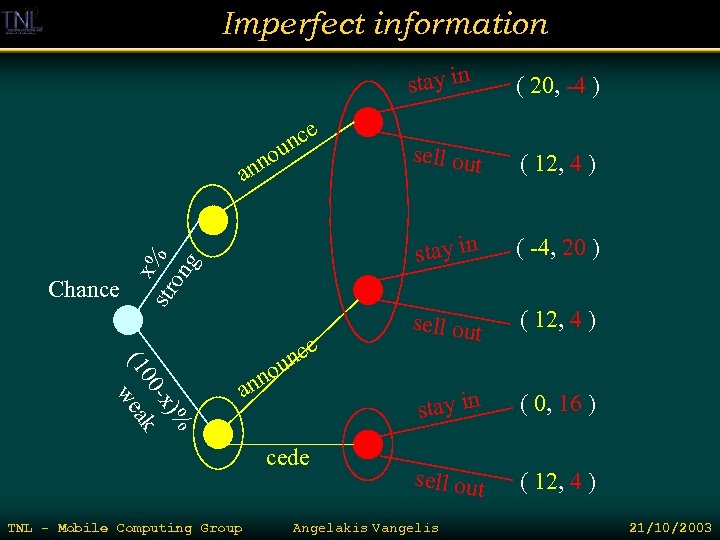
Imperfect information stay in x% str on g Chance )% -x 00 k (1 wea e nc u no an cede TNL - Mobile Computing Group ( 12, 4 ) ( -4, 20 ) sell out ( 12, 4 ) stay in no an sell out stay in e nc u ( 20, -4 ) ( 0, 16 ) sell out ( 12, 4 ) Angelakis Vangelis 21/10/2003
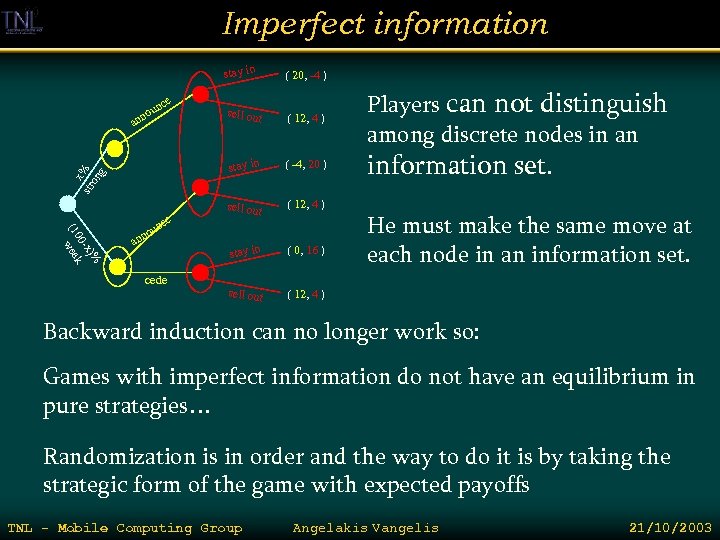
Imperfect information stay in x str % on g an )% -x 00 k (1 wea e nc an u no cede sell out ( 12, 4 ) stay in e nc u no ( 20, -4 ) ( -4, 20 ) sell out ( 12, 4 ) stay in ( 0, 16 ) sell out ( 12, 4 ) Players can not distinguish among discrete nodes in an information set. He must make the same move at each node in an information set. Backward induction can no longer work so: Games with imperfect information do not have an equilibrium in pure strategies… Randomization is in order and the way to do it is by taking the strategic form of the game with expected payoffs TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

Zero sum games The case of players playing fully opposed interest games embodies the class of two-player zero sum games. (rock-paper-scissors, chess, poker, pistol duels etc) In zero sum games the sum of all player utilities at each game solution is 0. An over-class are constant-sum games, where the sum of all utilities in each game solution is constant. Mixed strategies are intuitively the best solution for constant sum games with imperfect information. Usage of zero sum games along with randomized algorithms in online computation analysis. TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

Auctions & bidding English (open ascending bid) auction: “Do I have fifty? …Yes!…Do I have fifty-five? ” Simplified version: Second price auction offers made once over secure channels Highest bidder wins and pays the value of the second bidder. How to bid in a second price auction ? Use your private value of the object TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

Bidding private value Private value for an object is derived from needs and potential resell value estimated by each bidder. Bidding the private value in a second-price auction is a weakly dominant strategy. ie: regardless how others bid, no other strategy will get the bidder of private value better off. Examine what happens in different strategies: Bid lower than your private price Bid higher than your private price Same rationale works for the English auction TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

Common values Private values is most auctions a non realistic assumption. Art objects / memorabilia may be bought as investments but radio spectrum license is bought for business. The license value depends on market forces such as demand for mobile telephony. Such forces have a more or less common impact to all bidders. So we say that such auctions have common value aspects. What happens when we have pure common value? TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

The Winner’s Curse Uncertainty about the value jumps in. For our spectrum auction each company will conducted its own private market research to estimate retail demand each will come with slightly different results… The results of these estimates is correct on average, but the highest (winning) estimate and the lowest will deviate from the real value. . So playing like this and winning is bad news: the value has been overestimated and this is the winner’s curse… TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003

Further Reading www. gametheory. net R. Gibbons, Game Theory for Applied Economists Osborne, An Introduction to Game Theory Osborn and Rubinstein, A Course in Game Theory R. Axelrod, The Evolution of Cooperation Θεωρία Παιγνίων στο Ρέθυμνο http: //www. soc. uoc. gr/petrakis/8 ewria. php Marcus M. Mobius’ Game Theory Course http: //www. courses. fas. harvard. edu/~ec 1052/ The Role of Game Theory in Ad hoc Networks http: //www. cs. ucsb. edu/~ebelding/courses/595/s 04_gametheory/ Juha Leino Applications of Game Theory in Ad Hoc Networks TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003
TNL - Mobile Computing Group Angelakis Vangelis 21/10/2003
3f852529f4374cb00cfecbbc8323c49d.ppt