Множество – первичное понятие

Множество – первичное понятие математики «Объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью» «Множество есть многое, мыслимое нами как единое» Георг Кантор – создатель теории множеств

Множество – это совокупность каких-либо объектов

Какие из следующих множеств геометрических фигур на плоскости равны между собой? • А – множество всех квадратов • В – множество всех прямоугольников • С – множество всех прямоугольников с равными сторонами • D – множество всех прямоугольников с равными сторонами • F - Множество всех ромбов с прямыми углами

Для каждого из слов «Сосна» , «Осколок» , «Насос» , «Колос» составьте множество его различных букв. Имеются ли среди них равные множества?

Конечное множество состоит из конечного числа элементов

Пустое множество не содержит ни одного элемента

Бесконечное множество состоит из бесконечного числа элементов, т. е. это множество, которое не является ни конечным, ни пустым.

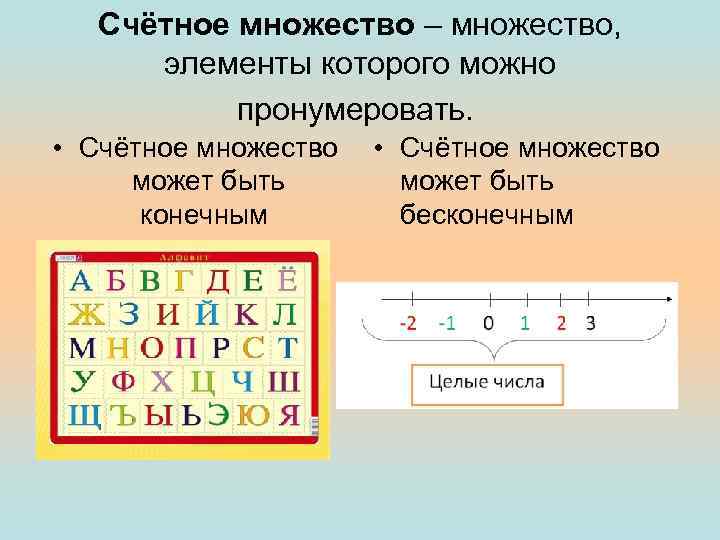Счётное множество – множество, элементы которого можно пронумеровать. • Счётное множество может быть конечным бесконечным

Способы задания множеств. Множество может быть задано следующим образом: – перечислением всех его элементов по их названиям (множество книг в библиотеке, множество учеников в классе, алфавит любого языка и т. д. ) – заданием общей характеристики ( общих свойств ) элементов данного множества (горячие напитки, собаки, семейство кошачих и т. д. ); – формальным законом построения элементов множества (Периодическая система элементов Менделеева и т. д. ). .

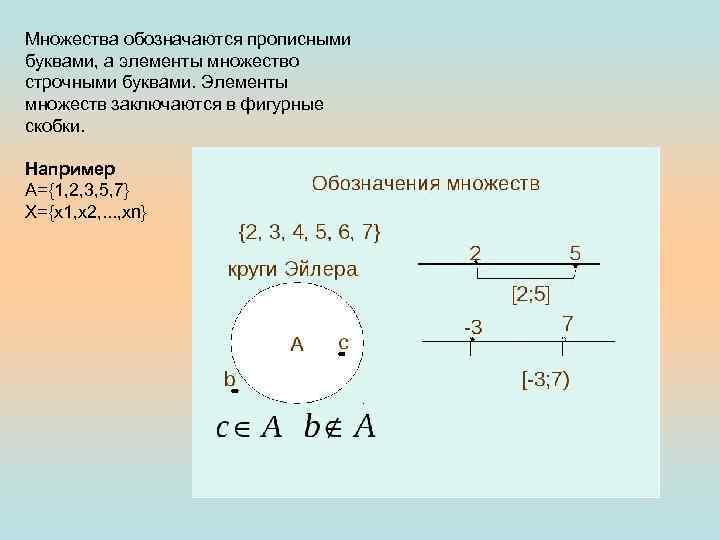Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки. Например А={1, 2, 3, 5, 7} Х={x 1, x 2, . . . , xn}

Операции над множествами

Включение Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит). Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).

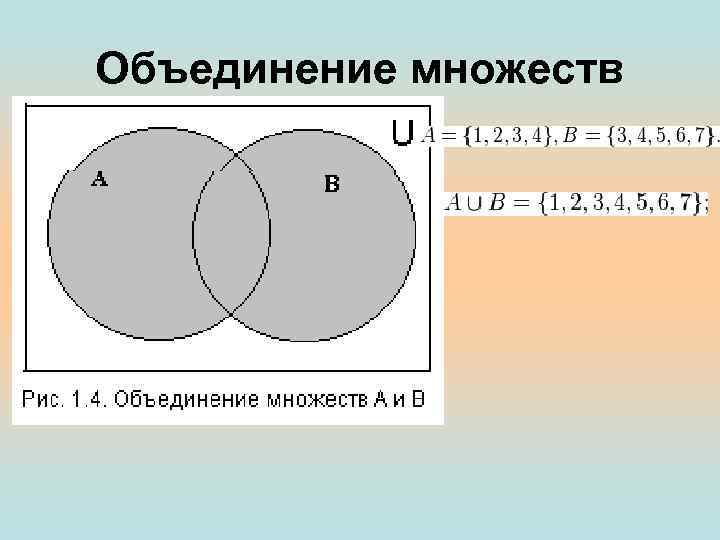Объединение множеств

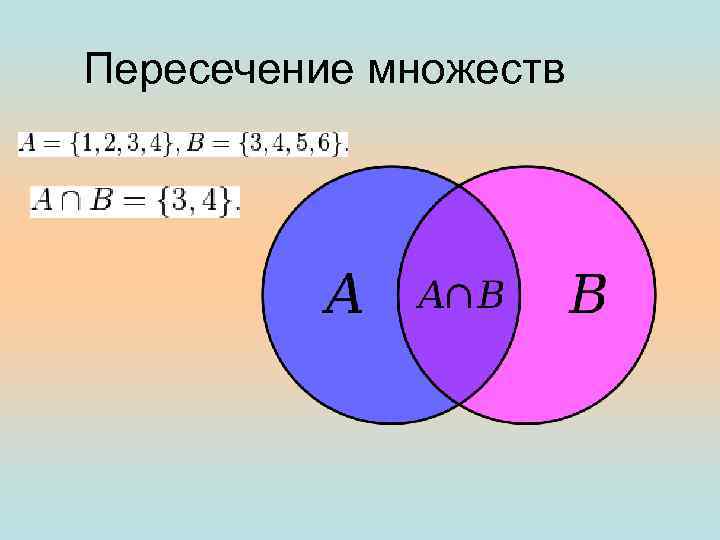Пересечение множеств

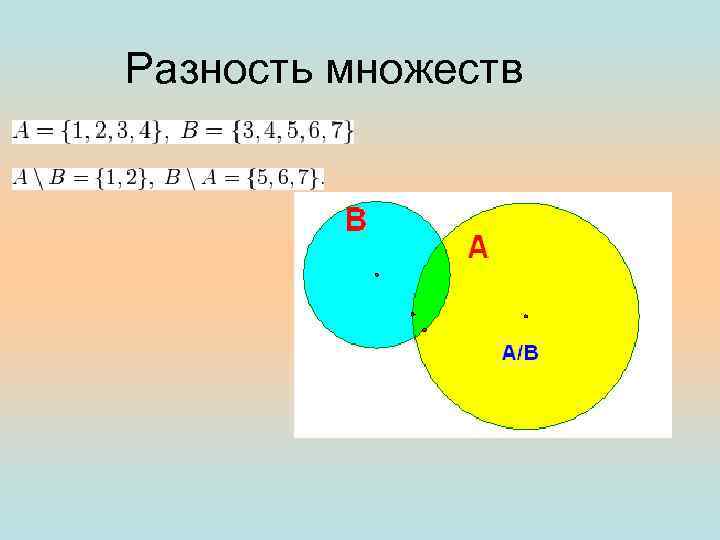Разность множеств

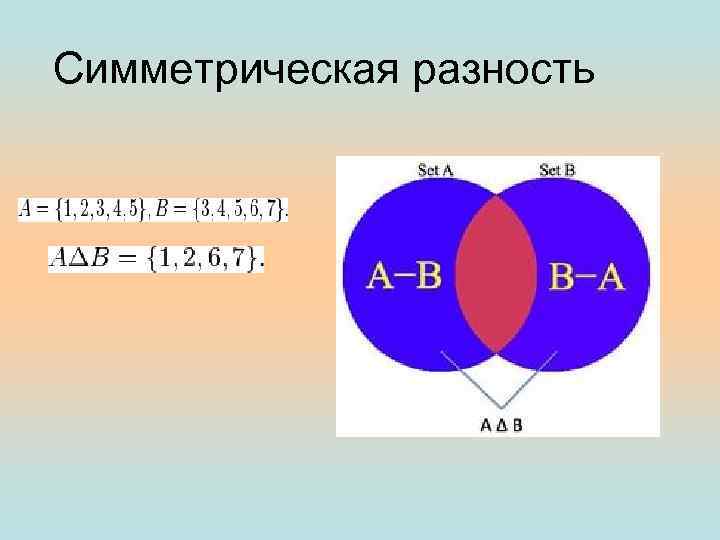Симметрическая разность